Hintergrund

Aufgrund der unterschiedlichen Anforderungen, die mathematische Aufgaben an Schülerinnen und Schüler stellen (vgl. ‚Anforderungsbereiche‘), ist es besonders in inklusiven Lerngruppen wichtig, neben allgemein bekannten Differenzierungsmaßnahmen eines zeitgemäßen Mathematikunterrichts weitere Formen der individuell angepassten Lernunterstützung sowie Erweiterung anzubieten (vgl. ,Planung von Förderung'). Das „Fünf-Stufen-Modell“ (vgl. Wember; s. auch PIKAS: Haus 6: Heterogenität – Fortbildungsmaterial – Zieldifferent lernen im gemeinsamen Unterricht) veranschaulicht hierbei das Spektrum an Erweiterungs- bzw. Unterstützungsstufen in inklusiven Lerngruppen (s. Abb. 2).

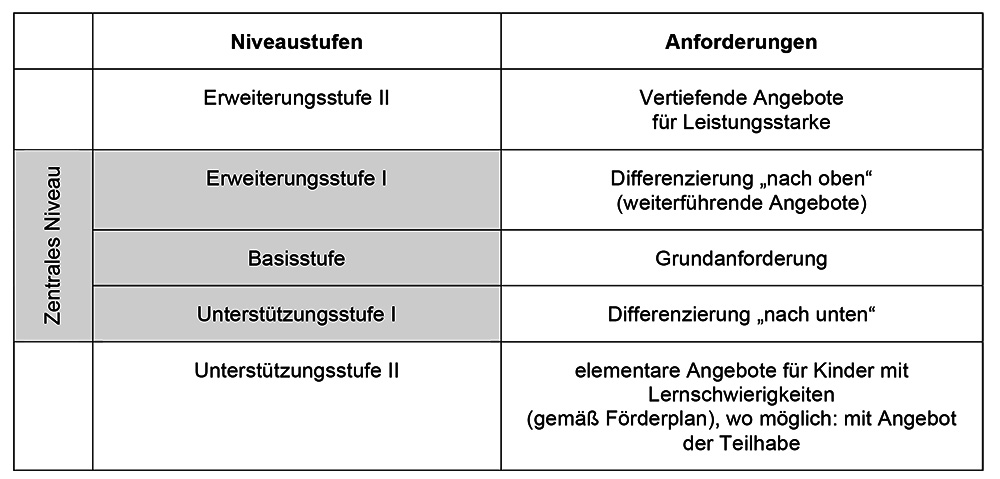Tabelle „Fünf-Stufen-Modell“ nach Wember. Zeile 1: Überschriften: „Niveaustufen“ und „Anforderungen“. Zeile 2: „Erweiterungsstufe II; Vertiefende Angebote für Leistungsstarke“. Zeile 3: „Erweiterungsstufe I; Differenzierung „nach oben“ (weiterführende Angebote)“. Zeile 4: „Basisstufe; Grundanforderung“. Zeile 5: Unterstützungsstufe I; Differenzierung „nach unten““. Zeile 6: „Unterstützungsstufe II; elementare Angebote für Kinder mit Lernschwierigkeiten (gemäß Förderplan), wo möglich: mit Angebot der Teilhabe“. Die drei Niveaustufen „Erweiterungsstufe I“, „Basisstufe“ und „Unterstützungsstufe I“ sind grau hinterlegt und als zentrales Niveau gekennzeichnet.
Abbildung 2: „Fünf-Stufen-Modell“ nach Wember

Neben der Berücksichtigung der allgemeinen Heterogenitätsspanne innerhalb von Schulklassen, welche als „zentrales Niveau“ deklariert wird, werden weitere Niveaustufen genannt, die über die Grenzen des allgemeinen Curriculums hinausgehen. Um allen Kindern das Lernen am gleichen Lerngegenstand zu ermöglichen, eignen sich Arbeitsaufträge, deren Inhalte an verschiedene Anforderungsniveaus angepasst werden können. Ausgehend vom gleichen inhaltlichen Kontext werden unterschiedliche Differenzierungsangebote bereitgestellt, um leistungsschwächere Kinder in ihrem Lernprozess zu unterstützen (Unterstützungsstufe I / II) sowie die Kompetenzen leistungsstärkerer Kinder zu erweitern (Erweiterungsstufe I / II). Dazu eignen sich beispielsweise Tippkarten (vgl. PIKAS: Haus 6: Heterogenität – Unterricht – Zahlenmauern-Übungsheft, Schüler-Material (Tippkarten)) oder Sternchenaufgaben.

Ausgehend vom Unterrichtsbeispiel „Tauschaufgaben“ soll nachfolgend in einer reduzierten Fassung dargestellt werden, wie ein dreistufiges Niveaustufen-Modell praktisch angewendet werden kann. Wobei im Erweiterungsbereich beispielhafte Herausforderungen und im Unterstützungsbereich beispielhafte Tipps zu finden sind.

Wir erforschen besondere Mal-Aufgaben: Tauschaufgaben

Haupt-Zielsetzung (Basis):

Die Schülerinnen und Schüler erkennen, dass das Ergebnis von Tauschaufgaben gleich ist, verdeutlichen ihre Entdeckungen und finden eine für sie angemessene Begründung.

Erweiterung

Entwicklung eines Beweises/ (non)-verbale Verallgemeinerung

 „Wie kannst du anderen Kindern erklären, warum das Ergebnis von Tauschaufgaben immer gleich ist? Schreibe deinen Tipp auf.“

Schüler:innenlösung: Die Aufgaben 3 mal 4 und 4 mal 3 sind jeweils als Punktebild dargestellt (Rechteck mit 4 Dreierreihen, Rechteck mit 4 Dreierreihen). Beide Rechtecke sind mit einem Doppelpfeil verbunden.

Schüler:innenlösung zur vorigen Abbildung. Das Kind schreibt: „Wenn man das Punktefeld aufeinanderlegt, dann ist es gleich“. (Rechtschreibung angepasst).

Übertragen der Entdeckungen auf Eigenproduktionen

„Erfinde eigene Tauschaufgaben.“

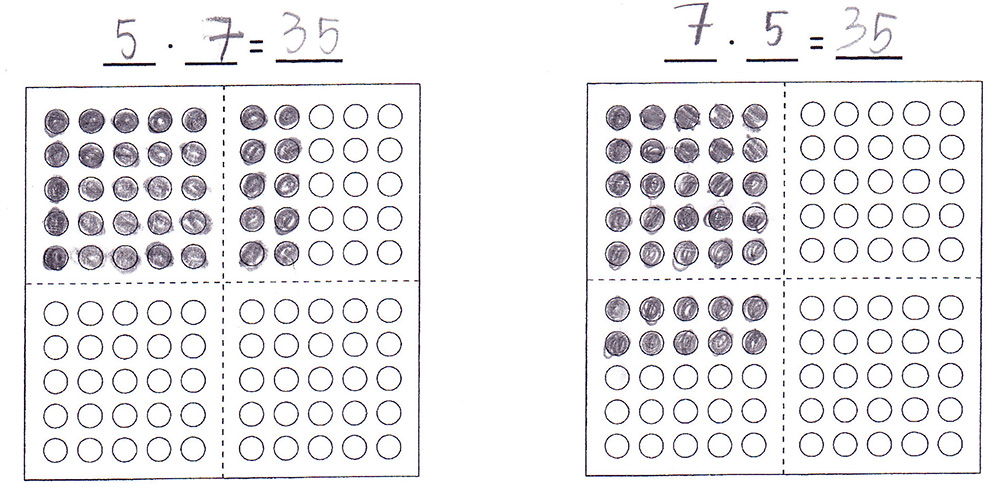
Schüler:innenlösung zur Aufgabe „Erfinde eigene Tauschaufgaben“: Die Aufgaben 5 mal 7 = 35 und 7 mal 5 = 35 wurden geschrieben, darunter jeweils ein leeres Hunderterfeld aus Punkten. Das Kind malt die Punkte entsprechend der Aufgaben aus.

Basis (inkl. Differenzierung)

Lösen der Multiplikationsaufgaben

„Rechne aus.“

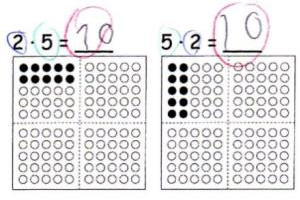
Multiplikationsaufgabe 2 mal 5 = 10 und 5 mal 2 = 10, darunter Darstellung der Aufgaben auf leerem Hunderterfeld mit Punkten. Schülerlösung zur Aufgabe „Rechne aus“: Die 10 wurde als Ergebnis eingetragen, die gleichen Faktoren der Tauschaufgaben und das Produkt wurden jeweils mit derselben Farbe eingekreist.

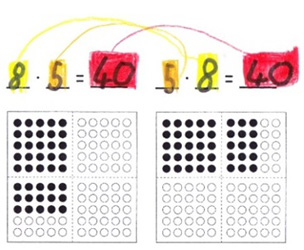
Schüler:innenlösung in der Entdeckungen mit Forschermitteln markiert wurden. Das Kind markiert die gleichen Faktoren der Tauschaufgaben und jeweils das Produkt mit derselben Farbe und verbindet sie mit einem Strich. Darunter: Darstellung der Aufgaben auf Hunderterfeldern mit Plättchen.

Aufstellen von Vermutungen über mathematische Zusammenhänge

„Was fällt dir auf? Markiere mit Forschermitteln.“

Schüler:innenlösung zur Aufgabe: „Was fällt dir auf? Markiere mit Forschermitteln“. Das Kind schreibt: „Ich habe herausgefunden, das Ergebnis immer gleich ist“ (Rechtschreibung angepasst).

Schüler:innenlösung zur Aufgabe: „Was fällt dir auf? Markiere mit Forschermitteln“. Das Kind schreibt: „Mir fällt auf, dass es immer die Tauschaufgabe ist. Und das Ergebnis ist immer gleich ist“ (Rechtschreibung angepasst).

Erklären von Beziehungen und Gesetzmäßigkeiten an Beispielen

„Warum ist das so? Begründe.“

Schüler:innenlösung zur Aufgabe: „Warum ist das so? Begründe“. Das Kind schreibt: „Wenn man die Punktefelder umdreht, dann ist das Ergebnis gleich“ (Rechtschreibung angepasst).

Unterstützung

Aufstellen von Vermutungen über mathematische Zusammenhänge (nonverbal bzw. mit unterstützenden Darstellungsmitteln oder einer Tippkarte)

„Was fällt dir auf? Markiere mit Forschermitteln.“

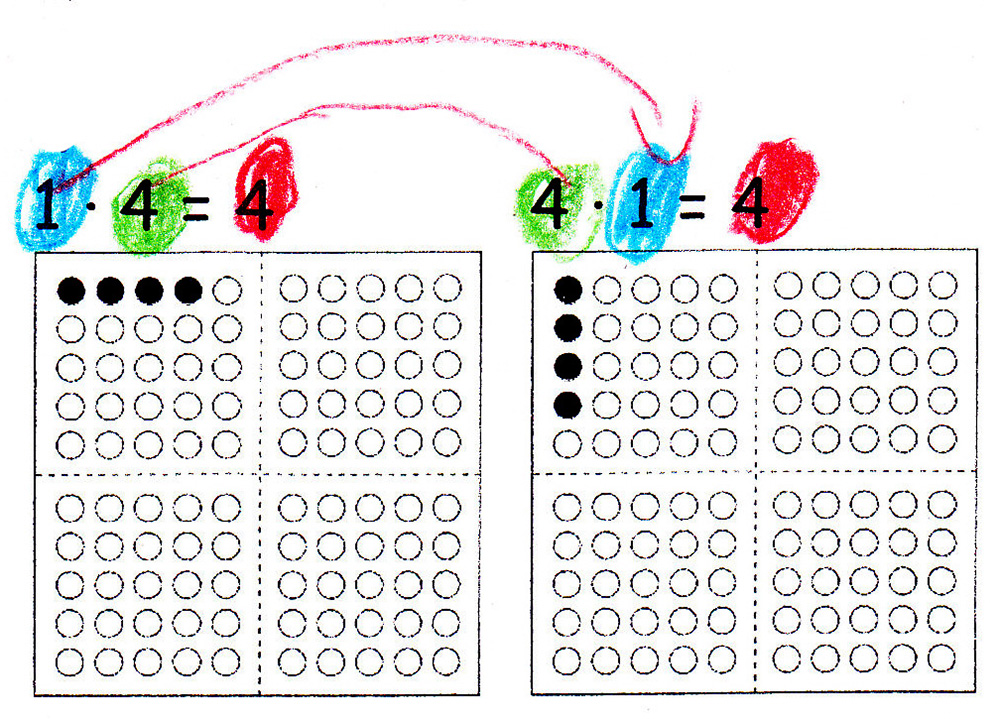
Schüler:innenlösung zur Aufgabe „Was fällt dir auf? Markiere mit Forschermitteln“: 1 mal 4 = 4 und 4 mal 1 = 4. Darunter: Darstellung der Aufgaben auf Hunderterfeldern mit Plättchen. Das Kind markiert jeweils die gleichen Faktoren der Tauschaufgaben und das Produkt mit derselben Farbe und verbindet sie mit einem Strich.

Bei der Nutzung von Forschermitteln kann die folgende Tippkarte unterstützend sein. Siehe außerdem PIKAS Haus 1: Forschermittel

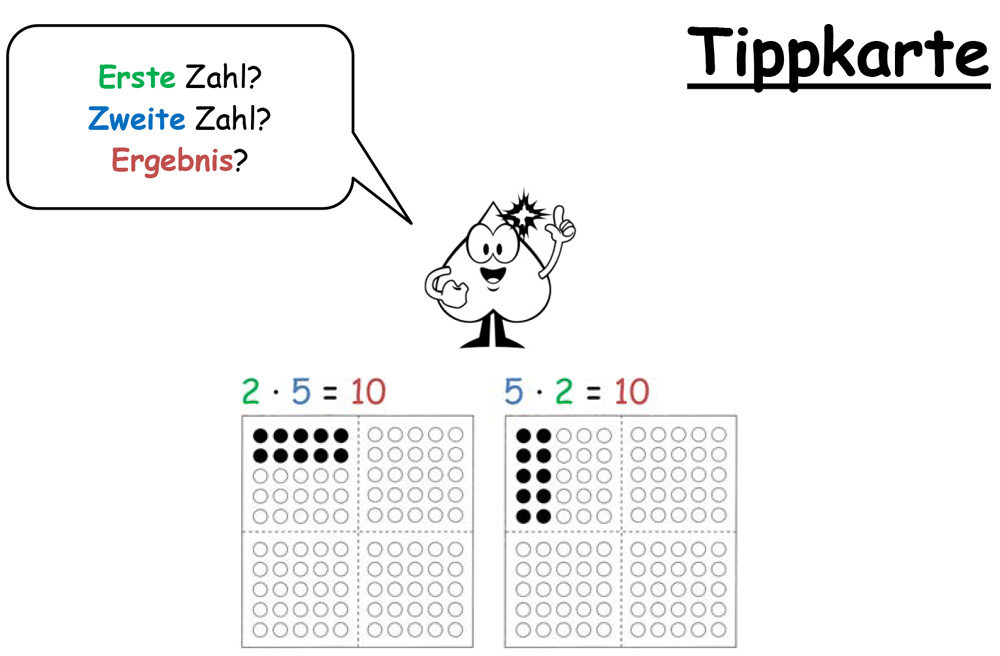
Oben rechts: Tippkarte. Mittig: Piko mit Sprechblase: In Grün „Erste Zahl?“. In Blau „Zweite Zahl?“. In Rot „Ergebnis?“. Unten: Symbolische Notation der Tauschaufgaben 2 mal 5 gleich 10 und 5 mal 2 gleich 10; die gleichen Faktoren und jeweils die Ergebnisse haben dieselben Farben und stimmen farblich mit den Texten in der Sprechblase überein. Darunter: Darstellung der Aufgaben auf Hunderterfeldern mit Plättchen.

Auch das Bereitstellen von Anschauungsmaterial kann die Kinder darin unterstützen, Grundvorstellungen zu Tauschaufgaben zu entwickeln und darszustellen.

Zwei Streifen mit jeweils vier Plättchen. Ein Streifen liegt vertikal, der andere horizontal.

 

Hier können Sie das Untersichtsbeispiel als PDF herunterladen

Kurz-URL: https://pikas-mi.dzlm.de/node/70

QR-Code downloaden