Speziell unter dem Gesichtspunkt eines inklusiven Mathematikunterrichts ist es wichtig, den Schülerinnen und Schülern unterschiedliche Zugänge zur Mathematik zu ermöglichen. Viele dieser Zugänge werden jedoch erst durch die Nutzung von sog. Forschermitteln eröffnet, da diese u.a. viele Anschauungs- und Darstellungsmittel (vgl. ‚Darstellungsformen‘) umfassen, mit denen Kinder ihre Denkprozesse auf verschiedene Art und Weise veranschaulichen können (s. auch ‚Gemeinsamen Austausch anregen: Sich verständlich machen‘).
Doch Forschermittel charakterisieren sich nicht allein in ihrer Funktion als Darstellungsmittel, mit deren Hilfe Übersetzungen zwischen verschiedenen Darstellungsformen vorgenommen werden können. Sie können auch als Strukturierungshilfe (z.B. Pfeile, Einkreisungen,…) dienen, wodurch das Entdecken, Darstellen, Begründen und Kommunizieren innerhalb einer Darstellungsform erleichtert wird. Grundsätzlich definieren sie sich durch drei eng miteinander in Verbindung stehender Funktionen, die für die Durchführung eines zeitgemäßen, kompetenzorientierten Mathematikunterrichts wesentlich sind.
Sie…
-
… helfen, mathematische Strukturen zu entdecken („Instrument des Forschens“).
-
… helfen, Entdecktes darzustellen („Instrument des Dokumentierens“).
-
… helfen über Dargestelltes zu kommunizieren („Instrument des Kommunizierens“).
Zum einen können Forschermittel Lernenden dazu verhelfen, Muster und Strukturen innerhalb einer mathematischen Aufgabenstellung besser zu erkennen und Erkanntes erneut zu fokussieren, zum anderen können sie aber auch dazu dienen, die selbst gemachten Ergebnisse dokumentarisch festzuhalten, um sich z.B. zu einem späteren Zeitpunkt besser daran erinnern zu können (vgl. Sundermann, 2014). Diese Dokumente können drittens auch dazu genutzt werden, um die Ergebnisse anderen Kindern besser zeigen und erklären zu können. Letzteres ist vor allem bei Schülerinnen und Schülern mit Schwierigkeiten im sprachlichen Bereich oftmals die einzige Möglichkeit, ihre Entdeckungen offenzulegen. Alle drei Funktionen fördern zudem die prozessbezogenen Kompetenzen jedes Kindes, wie z.B. das Darstellen und Kommunizieren (vgl. KIRA: Problemlösen & Co – Kompetenzen im Mathematikunterricht).
Ein Blick auf die Grafik unserer Startseite Mathe inklusiv mit PIKAS zeigt bereits einige der möglichen Forschermittel bei der Verwendung im Unterricht. Viele von ihnen sind universell einsetzbar, einige aber auch auf den aktuellen Unterrichtsgegenstand oder die jeweilige Klassensituation zugeschnitten. Jedes Forschermittel lässt viele Adaptions- und Erweiterungsmöglichkeiten zu, mit denen sich Schülerinnen und Schüler jedes Leistungsniveaus erreichen lassen.
Allem voran ist es aber wichtig, den Begriff des Forschermittels bereits frühzeitig einzuführen und genügend Zeit darin zu investieren, ihren Nutzen als Darstellungs- und Strukturierungshilfe mit den Kindern gemeinsam zu erarbeiten.
Zur Illustration:
Unser Partnerprojekt PIKAS (vgl. PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichtsmaterial – Forschermittelplakat) gibt bereits ein gewisses Grundrepertoire an Forschermitteln vor:
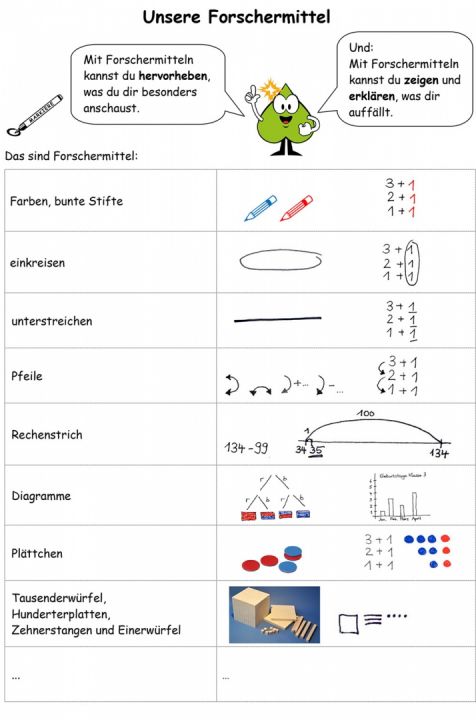 Abbildung 5
Abbildung 5
Diese Liste lässt sich, je nach Thema und Klassensituation, durch weitere Forschermittel (Tabellen, Bilder, Ziffernkarten, …) erweitern. Speziell im inklusiven Unterricht ist auch eine Adaption von Forschermitteln denkbar, wie die nachfolgenden Beispiele veranschaulichen:
 Abbildung 6a
Abbildung 6a
 Abbildung 6b
Abbildung 6b
Kleine oder filigrane Unterrichtsmaterialien sind für Lernende mit motorischen Schwierigkeiten eher von Nachteil, da sie von dem eigentlichen Lernprozess ablenken. Einige Forschermittel (Abb. 6a) lassen sich relativ einfach auch in einer größeren Version anfertigen, etwa als große Pappquadrate (Abb. 6b) für eine Unterrichtsreihe zu „Quadratmehrlingen“ (vgl. ‚Darstellungsformen‘). Sie können zudem als gut sichtbares Darstellungsmittel eingesetzt werden, beispielsweise in der Plenumsphase.
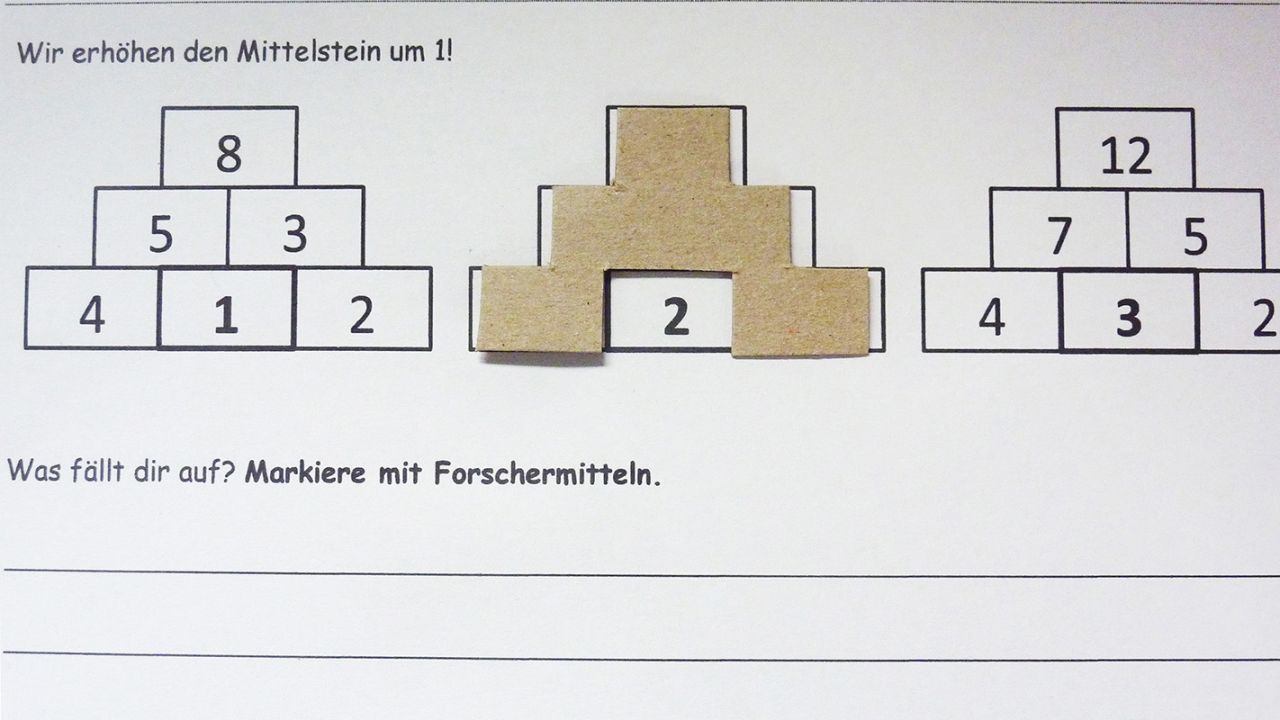 Abbildung 7a
Abbildung 7a
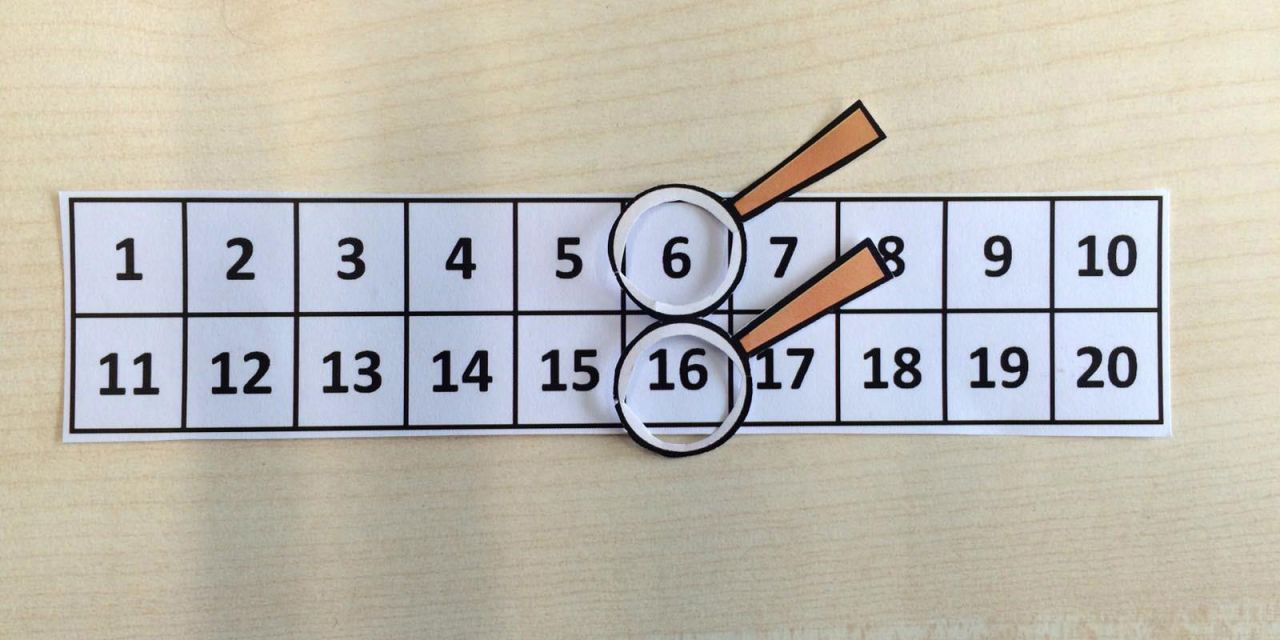 Abbildung 7b
Abbildung 7b
Lernende mit visuellen Schwierigkeiten könnte der Zugang zum Erforschen von Zahlenmauern erleichtert werden, indem sie entsprechende Schablonen (Abb. 7a) als Forschermittel nutzen. Diese können helfen, die Aufmerksamkeit auf einen bestimmten mathematischen Kontext (z.B. den Mittelstein) zu lenken. Eine ähnliche Funktion bietet das Verwenden einer Doppellupe, die die Beziehungen zwischen Zahlen innerhalb einer Zwanzigertafel fokussiert (Abb. 7b; vgl. Korten, i.V.).
 Abbildung 8a
Abbildung 8a
 Abbildung 8b
Abbildung 8b
Beschreibbare Kärtchen (Abb. 8a; Abb. 8b) können als Forschermittel dienen, wenn es sinnvoll ist, gefundene Ergebnisse zu strukturieren. Kindern, die nicht unmittelbar systematisch vorgehen, wird dadurch ermöglicht, mathematische Strukturen besser zu erkennen und ggf. fehlende Ergebnisse zu finden.
Neben der Förderung inhalts- sowie prozessbezogener Kompetenzen bringt das Verwenden von Forschermitteln einen weiteren positiven Nebenaspekt mit sich: Die Kinder werden wesentlich selbstständiger, da ihnen viele Möglichkeiten gegeben werden, eigenständig an ihren Ergebnissen zu forschen.