Anknüpfend an die Kriterien und Werkzeuge zur Erstellung von Diagnose- und Förderaufgaben, sollen im Folgenden einige praktische Umsetzungsmöglichkeiten vorgestellt werden. Im Anschluss daran, wird an einem konkreten Unterrichtsinhalt das Vorgehen beim Einsatz im Unterricht anhand von Schülerdokumenten erläutert.
Diagnoseaufgaben
Umsetzungsbeispiele im Unterricht
Im Unterricht gibt es verschiedene Methoden, Diagnoseaufgaben einzusetzen, auch hier ist wieder das eigentliche Ziel entscheidend. Möchte man punktuell die mathematischen Fähigkeiten zu einem ganzen Themenkomplex abfragen (z.B. die Kompetenzen im Tausenderraum oder zur Multiplikation), dann eignet sich beispielsweise der Einsatz einer Standortbestimmung. Ist aber ein regelmäßiger Einblick in die Leistungsstände der Kinder relevant, empfiehlt sich der Einsatz eines sog. Mathebriefkastens (vgl. Sundermann & Selter, 2006).
Aufgrund der unterschiedlichen Einsatzmöglichkeiten ist eine Kombination beider Methoden vorteilhaft. Nachfolgend sollen exemplarisch die beiden genannten Möglichkeiten vorgestellt werden.
Standortbestimmung
Die Standortbestimmung ist eine Sammlung verschiedener aussagekräftiger Diagnoseaufgaben (s. Abb. 5) zu einem bestimmten mathematischen Themenkomplex z.B. „Addition und Subtraktion im Tausenderraum“.

Abbildung 5:
Ausschnitt aus einer Standortbestimmung
Angewendet wird sie häufig zur Erfragung von Vorerfahrungen, wodurch sich der Unterricht besser an den Kenntnissen der Kinder ausrichten lässt (vgl. Voßmeier, 2012) oder zur Überprüfung des Lernzuwachses am Ende einer Unterrichtsreihe. Sie wird demnach punktuell eingesetzt. Im Anschluss an die Eingangs-Standortbestimmung wird diese für jedes Kind ausgewertet, um den Unterricht beispielsweise durch die Adaption von Aufgaben (vgl. ,Aufgaben adaptieren’) entsprechend auf die Lernstände der Kinder abzustimmen.
Weitere Informationen zum Thema Standortbestimmung sind auch bei unseren Partnerprojekten PIKAS: Haus 9: Lernstände wahrnehmen – Unterrichtsmaterial – Standortbestimmungen sowie primakom: Übergreifendes – Leistungen – Standortbestimmungen – Einstieg – Erhebung von Vorkenntnissen zu finden. Standortbestimmungen zu unterschiedlichen Inhaltsbereichen wie beispielsweise zu natürlichen Zahlen oder auch zu Brüchen, Prozenten und Dezimalzahlen sowie zugehörige Auswertungshilfen finden sich zudem in den Handreichungen des Projektes Mathe sicher können.
Mathebriefkasten
Der Mathebriefkasten (s. Abb. 6) ist ein Instrument, um ritualisiert und regelmäßig Diagnoseaufgaben im Unterricht einzusetzen und damit kontinuierlich die Lernstände zu erfassen.

Abbildung 6:
Mathebriefkasten
Die Kinder werfen eine entsprechende Diagnoseaufgabe („den Brief“) am Ende der Unterrichtsstunde, der Lerneinheit etc. in den Briefkasten. Anders als bei der Standortbestimmung handelt es sich nur um eine Aufgabe, dessen Bearbeitung nicht länger als ungefähr zehn Minuten in Anspruch nehmen sollte. Auch Aufgaben unabhängig vom aktuellen Unterrichtsthema sind für diese Methode geeignet. Beim „Mathe-Brief“ kann es sich um ein leeres Blatt handeln, auf dem von den Kindern die von der Lehrkraft gestellte Frage (z.B. Frage des Tages, Frage des Monats) notiert wird. Es besteht jedoch ebenfalls die Möglichkeit kleine vorgefertigte Arbeitsblätter einzusetzen (s. Abb. 7).

Abbildung 7:
Beispielaufgabe Mathebriefkasten
Im Anschluss an den Einsatz im Unterricht werden die Briefe der Kinder gesammelt und ausgewertet. So dienen sie zum einen zur weiteren Förderung, aber auch zur Dokumentation der Lernentwicklung. Weitere Informationen zum Thema Mathebriefkasten finden Sie auf PIKAS: Haus 9: Lernstände wahrnehmen – Unterrichtsmaterial – Mathebriefkasten.
Auswertung
Sowohl die Standortbestimmungen also auch die „Briefe“ des Mathebriefkastens werden von der Lehrkraft ausgewertet und zur weiteren Unterrichts- und Förderplanung genutzt (vgl. ,Planung von Förderung‘). Zur besseren Übersichtlichkeit bietet sich das Dokumentieren in tabellarischer Form an. Das Illustrationsbeispiel zeigt, wie eine solche Auswertungstabelle aussehen könnte.
|
Aufgabe: |
|
|
Inhaltsbezogene
Kompetenzen |
Prozessbezogene
Kompetenzen |
|
|
|
|
|
|
|
|
|
|
|
|
Name |
|
|
|
|
|
|
|
|
|
|
|
Anmerkungen (Vorgehensweise, Strategie, Besonderheiten, ...) |
|
|
Tabelle 4: Ausschnitt aus dem Leitfaden zur Auswertung der Mathebriefkastenaufgaben
|
Reflexion |
|
Name |
Folgerungen (inhaltlich, organisatorisch);
Wie muss es jetzt weitergehen? Welche Fördermaßnahmen können zum Einsatz kommen? |
|
|
|
Tabelle 5: Ausschnitt aus dem Leitfaden zur Auswertung der Mathebriefkastenaufgaben
Sollte die Auswertung der schriftlichen Ergebnisse nicht aussagekräftig genug sein, empfiehlt sich der Einsatz von kurzen Diagnosegesprächen, um der Ursache einer nicht oder falsch bearbeiteten Aufgabenstellung nachgehen zu können (vgl. ,Diagnose- und Fördergespräche‘).
Förderaufgaben
Umsetzungsbeispiele im Unterricht
Im Unterricht gibt es verschiedene Methoden, Förderaufgaben einzusetzen. Voraussetzung für ihren Einsatz ist zunächst die Auswahl von Aufgaben, die sich für das festgelegte Ziel eignen und den Kriterien „guter Aufgaben“ (s. Hintergrund; Kapitel 2.2) entsprechen. Neben dem Material des Projektes Mathe sicher können oder den auf dieser Homepage angebotenen Materialien eignen sich ebenso Aufgaben aus „guten Schulbüchern“. Nachfolgend sollen zwei Beispiele vorgestellt werden, wie Förderaufgaben methodisch in den Unterricht integriert werden können.
Möchte man punktuell die mathematischen Fähigkeiten zu einem bestimmten Thema fördern (z.B. das Finden von Multiplikationsaufgaben zu Sachsituationen und umgekehrt), dann eignet sich beispielsweise der Einsatz von Förderaufgaben im Rahmen einer Mathe-Sammlung. Geht es aber eher darum, einen mathematischen Sachverhalt regelmäßig zu üben oder zu vertiefen, empfiehlt sich der Einsatz einer Mathe-Kartei. Aufgrund der unterschiedlichen Einsatzmöglichkeiten ist eine Kombination beider Methoden vorteilhaft. Nachfolgend sollen exemplarisch die beiden genannten Möglichkeiten vorgestellt werden.
Mathe-Sammlung
Die Mathe-Sammlung ist eine Sammlung verschiedener mathematischer Aufgabenstellungen (s. Abb. 8) zu einem bestimmten Themenkomplex z.B. „Einführung der Multiplikation“. Die Lernenden heften in dieser Mathe-Sammlung die erledigten Arbeitsaufträge des entsprechenden Themas d.h. auch ergänzende Förder- oder Erweiterungsaufgaben ab, wodurch jede Sammlung sehr individuell zusammengestellt ist. Wann ein Kind eine Förderaufgabe oder aber eine Erweiterungsaufgabe benötigt (s. auch ‚Tipps und Herausforderungen‘), sollte aus den Ergebnissen der kontinuierlichen Diagnose abgeleitet werden, d.h. der Einsatz der Förderaufgaben geschieht hier unterrichtsintegriert und punktuell an entsprechenden Stellen des Lernprozesses.

Abbildung 8:
Ausschnitt aus einer Mathe-Sammlung
Fördermaterialien zu unterschiedlichen Themengebieten, die zur Ergänzung so einer Mathe-Sammlung genutzt werden können, finden sich nicht nur bei ,Mathe inklusiv‘, sondern beispielsweise auch in den Handreichungen des Projektes Mathe sicher können.
Mathe-Kartei
Die Mathe-Kartei (s. Abb. 9) ist eine Lern- und Förderkartei, in der zu unterschiedlichen Themengebieten eine Vielzahl von Förderaufgaben gesammelt werden können. Diese sollte kontinuierlich in der Klasse aufgestellt bleiben und an geeigneten Stellen des Lernprozesses unterrichtsergänzend z.B. im Förderunterricht, bei der Wochenplanarbeit etc. zum Einsatz kommen. Die Arbeit mit der Kartei kann auch unabhängig vom aktuellen Unterrichtsthema stattfinden, um vorausgegangene Inhalte aufzuarbeiten oder zu vertiefen.

Abbildung 9:
Mathe-Kartei
Die Aufgaben sollten so gestaltet sein, dass sie nicht nur in Einzelarbeit, sondern vermehrt auch in Partner- oder Kleingruppenarbeit durchführbar sind (vgl. ,Gemeinsamen Austausch anregen‘). Im Gegensatz zur Mathe-Sammlung, die ein individuelles Instrument darstellt, steht die Mathe-Kartei der ganzen Klasse in gleicher Form zur Verfügung. Die Lehrkraft kann aber trotzdem entscheiden, wann welches Kind eine Karteikarte zur Förderung nutzen sollte. Es eignen sich hier besonders Aufgabenstellungen, bei denen Handlungen am Material durchgeführt werden müssen. Teilweise ist es aber auch sinnvoll, die Lernenden dazu aufzufordern etwas in ihr Heft oder auf einem leeren Blatt zu notieren. Da die Handlungsorientierung hier aber im Fokus steht, werden außer der Karteikarte keine zusätzlichen Arbeitsblätter benötigt.
Auswertung
Die Aufgabenauswertung der Mathe-Sammlung bzw. der Mathe-Kartei ist je nach Bearbeitungsart (schriftlich oder handelnd) unterschiedlich. Bei allen schriftlichen (nachvollziehbaren) Dokumenten kann problemlos der Leitfaden zur Auswertung von Diagnoseaufgaben genutzt werden (s. Hintergrund; Kapitel 2.1.3). Bei Handlungen, mündlichen Bearbeitungen etc. spielt die Beobachtung (im Idealfall mit Hilfe eines Beobachtungsleitfadens; s. beispielsweise Tabelle 6) bei der Auswertung eine wesentliche Rolle, wobei hier die Zusammenarbeit mit einer sonderpädagogischen Fachkraft zu empfehlen ist.
|
Beobachtungsleitfaden |
|
Mathematischer Inhalt |
|
|
Geforderte Kompetenz |
|
|
Beispielhafte Aufgabenstellung |
|
|
Beobachtungsschwerpunkte |
Anmerkungen |
|
|
|
Tabelle 6: Ausschnitt aus einem Beobachtungsleitfaden
Beispiel für eine Praktische Umsetzungsmöglichkeit von Diagnose- und Förderaufgaben
Am gewinnbringendsten ist der Einsatz einer Kombination aus den dargestellten Umsetzungsbeispielen, welche im inklusiven Unterricht am besten in Zusammenarbeit mit einer sonderpädagogischen Fachkraft funktioniert.
Das folgende Beispiel entstammt einer Unterrichtsreihe zum Thema Wahrscheinlichkeit („Wahrscheinlichkeiten – Wie wahrscheinlich ist ein Gewinn?“) und soll exemplarisch darstellen, wie bei der Kombination von Diagnose- und Förderaufgaben praktisch vorgegangen werden kann. Die gezeigten Dokumente der durchgeführten Unterrichtsreihe entstammen aus einer aus 17 Schülerinnen und Schülern bestehenden vierten Klasse mit sehr heterogenen Lernvoraussetzungen. In der inklusiven Lerngruppe befinden sich u.a. Kinder mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ und erhöhtem Unterstützungsbedarf im „sozial-emotionalen Bereich“. Die Klasse weist zudem einen hohen Anteil von Kindern auf, die Deutsch als Zweitsprache erlernen.
Vor dem Einsatz der Diagnoseaufgaben im Unterricht wurde entsprechend der Planungsschritte für Diagnoseaufgaben vorgegangen (s. auch Hintergrund; Kapitel 2.1)
Planungsschritte für den Einsatz von Diagnoseaufgaben
-
Mathematischen Inhalt festlegen und Schwerpunkte setzen
-
Auf Grundlage des gegenwärtigen Unterrichtsinhalts und der Lernvoraussetzungen der Kinder wurde der mathematische Inhalt festgelegt. Die Lehrkraft hat sich für den Bereich „Daten, Häufigkeiten und Wahrscheinlichkeiten“ mit dem Schwerpunkt „Wahrscheinlichkeiten“ (MSW, 2008, S. 66) entschieden.
-
Geforderte Kompetenz(en) auswählen
-
Die geforderte Kompetenz war insbesondere, das Beschreiben der Wahrscheinlichkeit von einfachen Ereignissen und ggf. das Bestimmen der Anzahl verschiedener Möglichkeiten (vgl. MSW, 2008, S. 66).
-
Aufgabe(n) und Material auswählen
-
Passend zum Inhalt und den zugehörigen Kompetenzen wurden Aufgaben so adaptiert, dass sie als Diagnoseaufgabe fungieren können (vgl. Abb. 10). Als Anschauungsmaterial diente in diesem Beispiel ein normaler Spielwürfel.
Ergänzend zur Diagnoseaufgabe aus dem Mathematikbuch wurden im Beispiel aus Abbildung 10 eine weitere Fragestellung, sowie ein Feld zur schriftlichen Bearbeitung hinzugefügt, um die Aufgabe diagnostisch informativer und offener zu gestalten. Des Weiteren wurde durch das Hinzufügen des Auftrags „Begründe.“ eine Reflexion von den Kindern eingefordert (s. Hintergrund; Kapitel 2.1).

Abbildung 10:
Diagnoseaufgabe
Nachdem die Kinder im Unterricht mit dem Thema „Wahrscheinlichkeiten“ erste Erfahrungen gesammelt haben und einige Experimente mit einem Würfel durchgeführt wurden, wollte die Lehrkraft wissen, inwieweit die Kinder die Würfelexperimente verinnerlicht haben, um zum nächsten Experiment übergehen zu können. Damit die Diagnose unterrichtsbegleitend geschehen konnte und sich der Fokus zunächst auf eine einzelne Aufgabe richten sollte, hat sie sich für die Methode des „Mathebriefkastens“ entschieden. Die Bearbeitung der Kinder zeigte dabei noch ein sehr heterogenes Bild bezüglich des Wahrscheinlichkeitsverständnisses (vgl. Abb. 11-16).

Abbildung 11: Alina |

Abbildung 12: Merle |

Abbildung 13: Justus |

Abbildung 14: Luis |

Abbildung 15: Marlon |

Abbildung 16: Lara |
Während beispielsweise bei Justus (Abb. 13) noch zu klären war, ob ihm die Unterscheidung der Regeln zu einem Spiel wie z.B. „Mensch ärgere dich nicht“ überhaupt bewusst war, stand bei Lara (Abb. 16; „weil fast jede Zahl durch zwei teilbar ist“) aufgrund ihrer Aussage fest, dass sie hinsichtlich des Verständnisses der Teilbarkeit von Zahlen noch einmal genauer diagnostiziert und möglicherweise gefördert werden sollte. Im Folgenden ist die weitere Vorgehensweise anhand der Förderung von Alina (Abb. 17) und Luis (Abb. 18) genauer dargestellt.

Abbildung 17: Alina |

Abbildung 18: Luis |
Mit Hilfe eines Leitfadens (vgl. Abb. 19-20) wurden die Ergebnisse der Lernenden dokumentiert und genauer ausgewertet, woraus Folgerungen für die weitere Vorgehensweise zur Förderung abgeleitet wurden (s. Hintergrund; Kapitel 2.1).
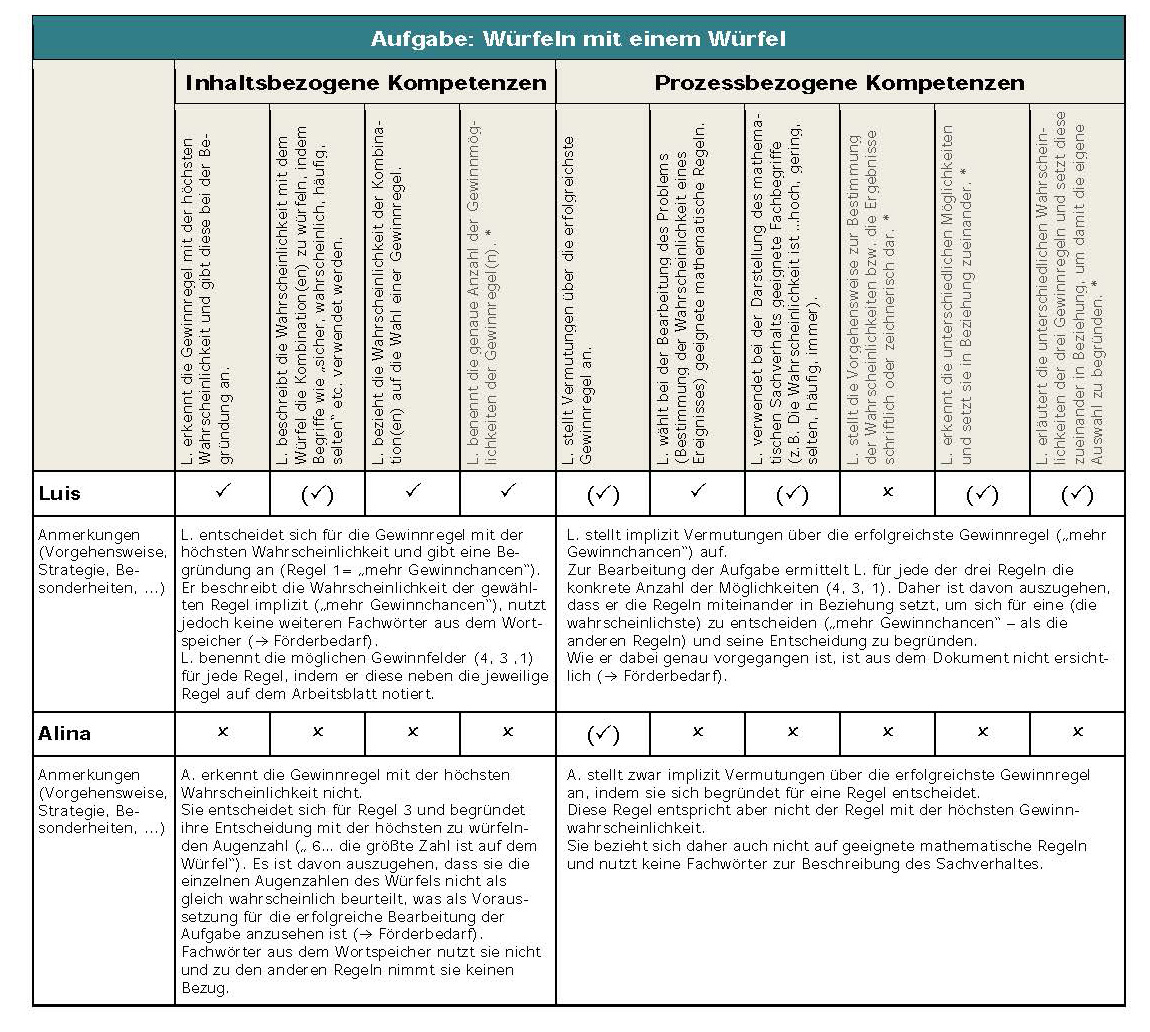
Abbildung 19:
ausgefüllter Leitfaden für die Mathebriefkastenaufgabe „Würfeln mit einem Würfel“

Abbildung 20:
Reflexion der Mathebriefkastenaufgaben
Je nach individueller Situation kann der Leitfaden auch handschriftlich und stichpunktartig ausgefüllt werden (s. Abb. 21 – Abb. 22).
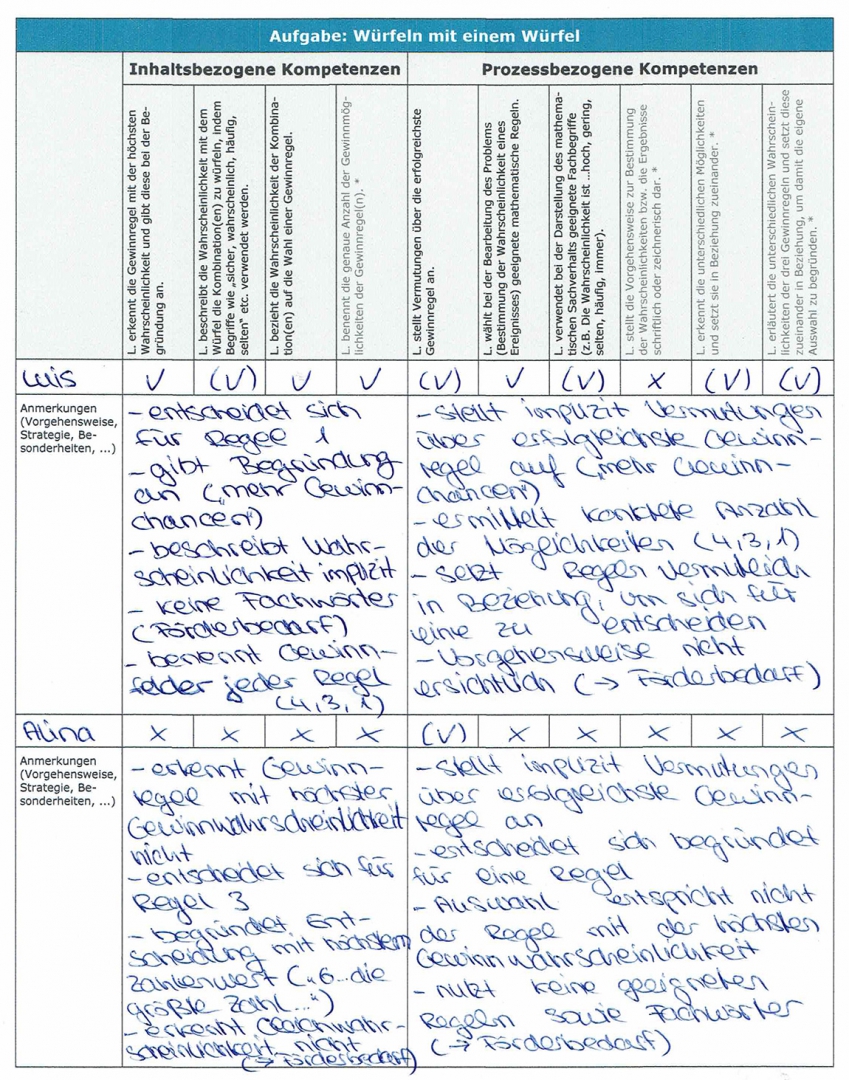
Abbildung 21:
ausgefüllter Leitfaden für die Mathebriefkastenaufgabe „Würfeln mit einem Würfel“ (handschriftlich)
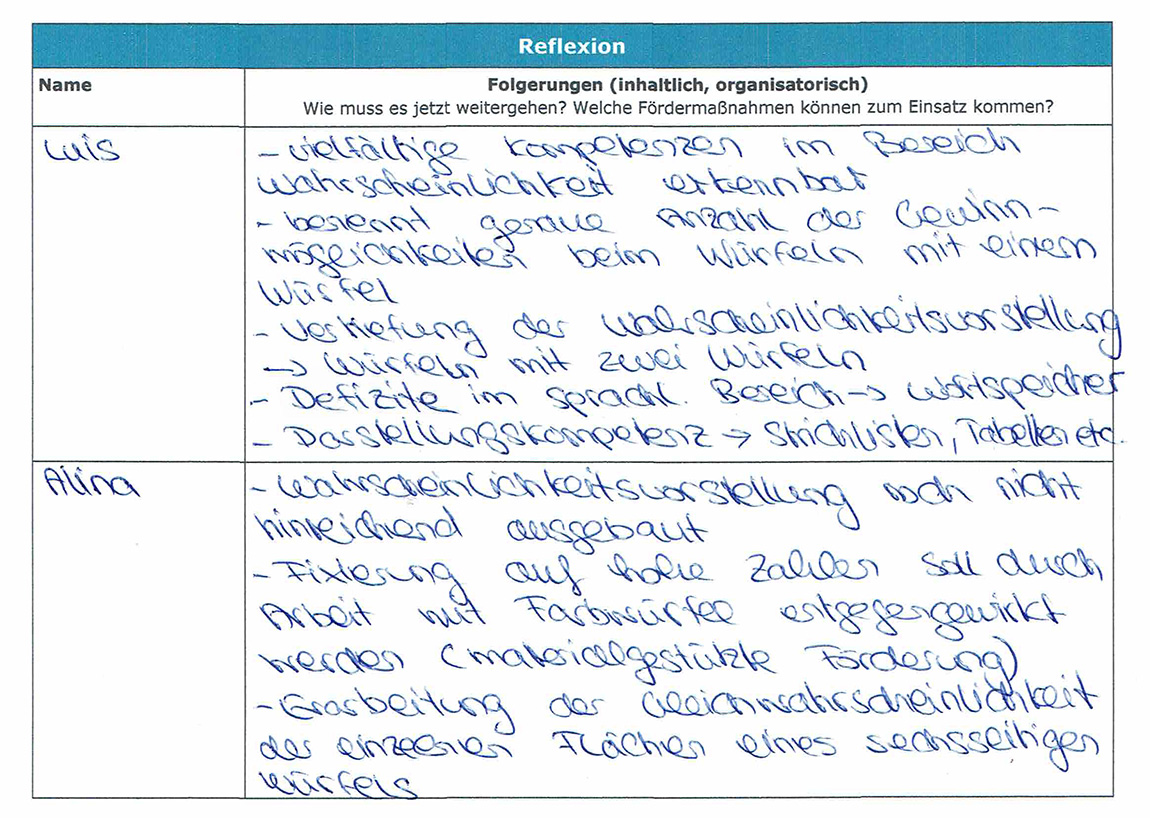
Abbildung 22:
Reflexion der Mathebriefkastenaufgaben (handschriftlich)
Entsprechend der Folgerungen aus der Analyse der Diagnoseaufgabe wurden die geforderten Kompetenzen noch weiter konkretisiert. Alina sollte beispielsweise das „Beschreiben der Wahrscheinlichkeit von einfachen Ereignissen“ am Ende der Förderung beherrschen. Da sie sich in der Diagnoseaufgabe sehr auf den hohen Zahlenwert fixierte, wurde zum Einstieg in die Förderung ein Farbwürfel genutzt. Zunächst arbeitete sie mit einer Karte aus der Mathe-Kartei. Die Aufgabe aus der Diagnose wurde variiert, indem Alina nun mit einem Farbwürfel würfeln sollte. Wichtig war bei ihr zudem der Fokus auf der Handlungsorientierung (s. Hintergrund; Kapitel 2.2), da auch ein Gespräch mit ihr zeigte, dass sie die Gleichwahrscheinlichkeit der einzelnen Augensummen noch nicht verinnerlicht hatte.
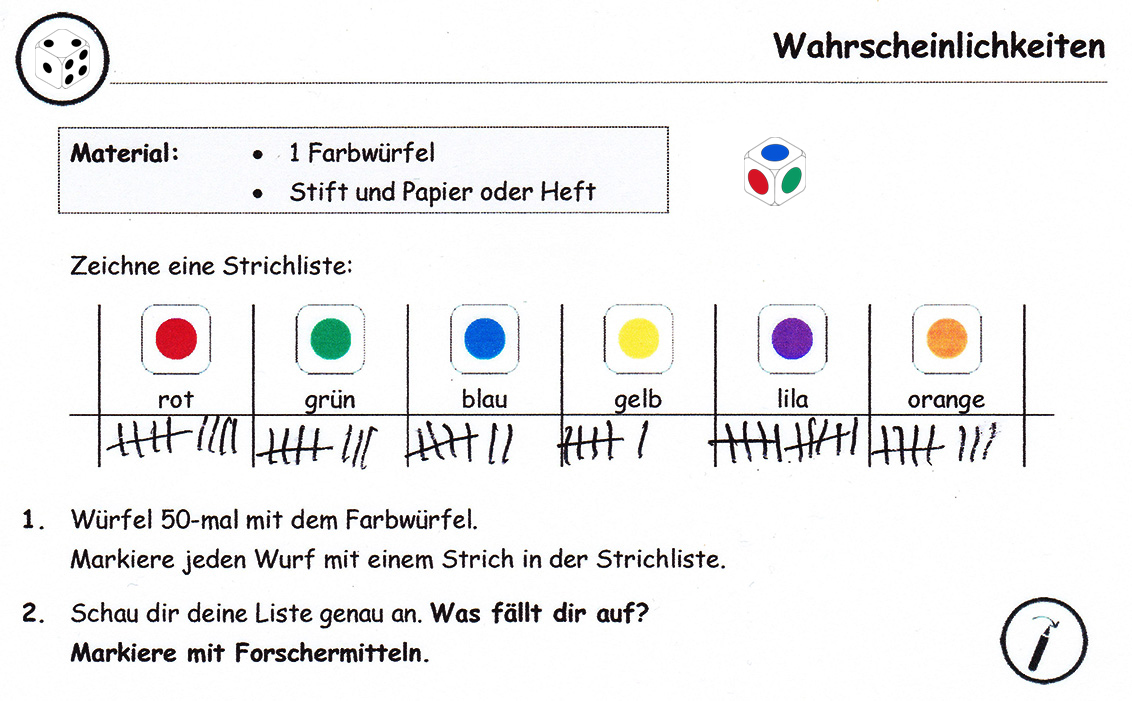
Abbildung 23:
Förderaufgabe aus der Mathe-Kartei
In einem Reflexionsgespräch wurde mit Alina über ihre Entdeckungen gesprochen. Dabei verdeutlichte sich, dass ihr, anders als beim Zahlenwürfel, auffiel, dass die Farben ungefähr gleich oft gewürfelt wurden (Abb. 24).

Abbildung 24
In der weiteren Förderung arbeitete Alina in ihrer Mathe-Sammlung mit verschiedenen Wahrscheinlichkeits-Aufgaben (Abb. 25), in denen zunächst ausschließlich der Farbwürfel Verwendung fand. Analog zu den Zahlenwürfel-Aufgaben der anderen Kinder sollte Alina beispielsweise die Wahrscheinlichkeitsregeln des Farbwürfels auf ein Würfelnetz übertragen, wodurch ein Wechsel von der Handlung auf eine bildliche Darstellung initiiert wurde.

Abbildung 25:
Förderaufgabe aus der Mathe-Sammlung
Als Abschluss der Förderung sollte Alina nochmals die Mathebriefkastenaufgabe vom Beginn in leicht abgeänderter Form bearbeiten. Dabei fiel auf, dass sie die Erkenntnis der Gleichwahrscheinlichkeit der Flächen, auf die Aufgabe mit dem Zahlenwürfel nun korrekt übertragen konnte (Abb. 26).

Abbildung 26:
Mathebriefkasten-Aufgabe
Das Dokument von Luis (Abb. 18) zeigt schon ein gutes Wahrscheinlichkeitsverständnis. Auch für ihn wurden die Kompetenzen weiter konkretisiert. Das „Beschreiben der Wahrscheinlichkeit von einfachen Ereignissen und das Bestimmen der Anzahl verschiedener Möglichkeiten“ sollte bei ihm weiter vertieft werden. Entsprechend der Folgerungen aus der Analyse der Diagnoseaufgaben arbeitete Luis mit Karten aus der Mathe-Kartei (Abb. 27), in denen bereits Aufgaben mit zwei Würfeln gestellt wurden, die das Finden aller Kombinationsmöglichkeiten thematisierten. Der Fokus lag bei ihm auf dem Anbahnen tiefergreifender Einsichten („Warum ist da so?“), aber auch auf dem Anregen zum Verbalisieren (s. Hintergrund; Kapitel 2.2).
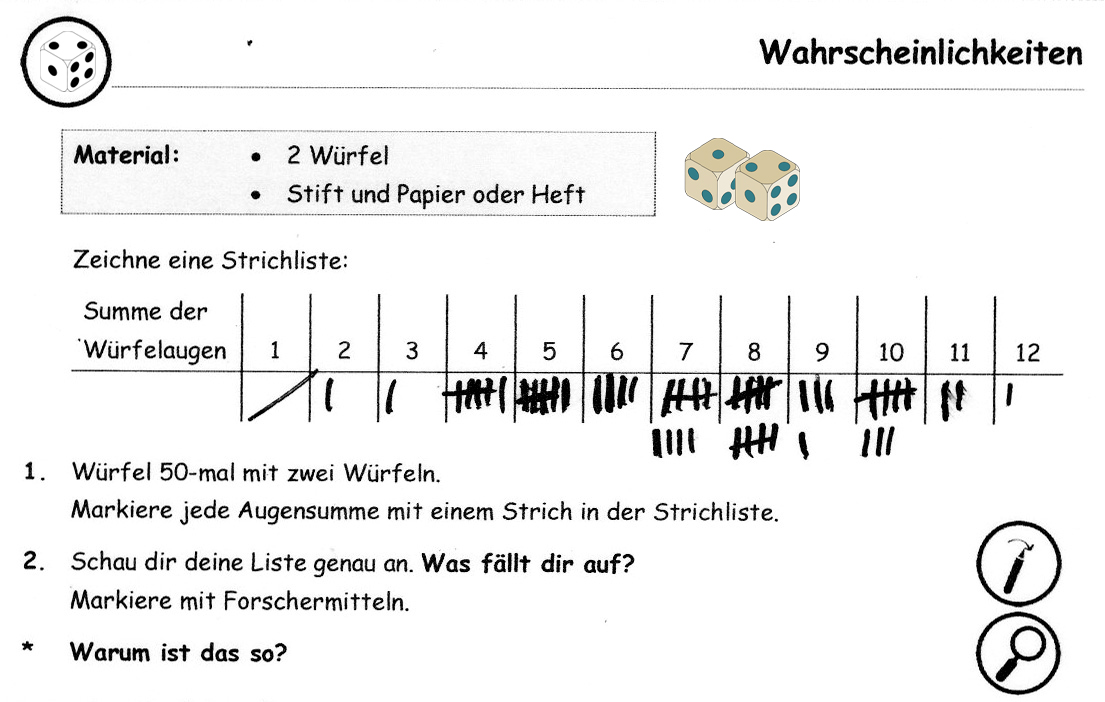
Abbildung 27:
Förderaufgabe aus der Mathe-Kartei
Zu Beginn würfelte er mit zwei Würfeln und erstellte eine Strichliste. Seine gemachten Entdeckungen hielt er wie folgt fest:

Abbildung 28
Eine Analyse seiner Beschreibung zeigt, dass Luis seine bisherigen Erkenntnisse zum Thema Wahrscheinlichkeit weiter ausdifferenzieren konnte. Durch das Würfeln mit zwei Würfeln und das Anfertigen einer Strichliste, erkannte er schon wesentliche Aspekte, beispielsweise, dass der Wurf einer 1 gar nicht möglich ist und dass das Werfen einer 2 oder 12 sehr unwahrscheinlich ist. Luis hatte jedoch noch Probleme seine zahlreichen Entdeckungen zu formulieren, weshalb der Wortspeicher (vgl. Abb. 29) immer wieder hinzugezogen wurde.

Abbildung 29:
Wortspeicher zum Thema „Wahrscheinlichkeit“
Im weiteren Verlauf der Förderung arbeitete auch Luis in seiner Mathe-Sammlung mit differenzierten Arbeitsblättern (vgl. Abb. 30), bei denen es um das Würfeln mit zwei Würfeln und das Darstellen der Kombinationsmöglichkeiten z.B. als Plusaufgabe oder Würfelbild geht.
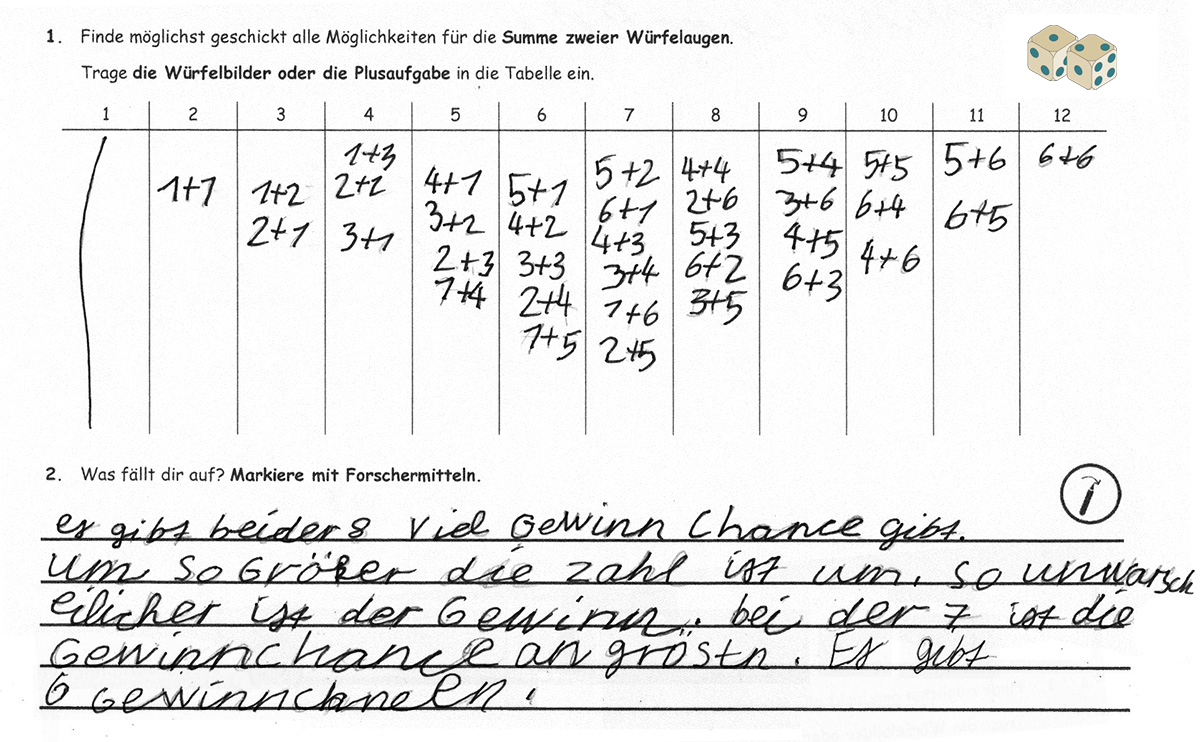
Abbildung 30:
Förderaufgabe aus der Mathe-Sammlung
Als Abschluss der Förderung wurde für Luis eine Mathebriefkasten-Aufgabe (Abb. 31) konzipiert, welche der Aufgabe zu Beginn der Unterrichtseinheit sehr ähnlich ist. Allerdings ging es dieses Mal um zwei Würfel, angepasst an den Verlauf seiner bisherigen Förderung.

Abbildung 31:
Mathebriefkasten-Aufgabe
Entsprechend des Diagnose- und Förderkreislaufs wurden die Ergebnisse aus der Förderung und der weiteren Diagnose anschließend erneut dokumentiert und ausgewertet, um die Entwicklung der Lernenden hinsichtlich weiterer Fördermöglichkeiten beurteilen zu können.
Weitere Anregungen
Anknüpfend an eine durchgeführte Diagnose und eine zunehmend erfolgreiche Förderung eignen sich Förderaufgaben im Sinne der Leitideen (s. Hintergrund; Kapitel 2.2) an geeigneten Stellen auch zur Durchführung in Partnerarbeit, beispielsweise durch entsprechende Aufgaben auf Karten der Mathe-Kartei (Abb. 32, s. auch Material). Bei den Kindern des folgenden Beispiels wurden zuvor Defizite im Stellenwertverständnis diagnostiziert, welche anschließend durch spezifische Fördergespräche unter Verwendung des Vierphasenmodells allmählich beseitigt wurden (vgl. ,Diagnose- und Fördergespräche‘). Um ihr neues Wissen zu festigen, empfiehlt es sich nun das bisher Erarbeitete durch geeignete „Aufgaben zum Üben“ (s. Hintergrund; Kapitel 2.2) zu vertiefen.
Da die Kinder das Vorgehen nach dem Vierphasenmodell ausgiebig kennengelernt haben, wäre es nach einer kurzen Einweisung (vgl. Video „Einführung Vierphasenmodell“) nun möglich, die Förderaufgabe zum Stellenwertverständnis in Partnerarbeit durchzuführen (vgl. Video „Zwei Kinder arbeiten nach dem Vierphasen-Modell“). Dies entlastet die Lehrkraft und kann bei den Kindern aufgrund des spielerischen Ansatzes dazu führen, die Aufgabe mit mehr Motivation zu lösen.
Abbildung 32:
Vierphasenmodell-Karte
Einführung Vierphasenmodell
Zwei Kinder arbeiten nach dem Vierphasenmodell
Weitere Hinweise zur Nutzung des Vierphasenmodells finden sich auch bei PIKAS: Vierphasenmodell.