Abbildung 1: Übersicht_Aufgabenstellung kompakt "Zahlen zerlegen"
Download Übersicht
Basisaufgabe
"Immer 6 (5; 7; ...). Zerlege, finde verschiedene Möglichkeiten."
Material: Wendeplättchen / Legerahmen / Stift / Papierstreifen mit 6 Punkten
Die Kinder arbeiten in Partnerarbeit. Vor ihnen liegen 6 Wendeplättchen. Ein Kind zerlegt die in einer Reihe angeordneten Plättchen in zwei Teilmengen. Das Partnerkind beschreibt die Zerlegung. Anschließend wechseln die Kinder die Rollen.
Abbildung 2
Die sprachliche Begleitung der Handlung ist hierbei besonders wichtig und sollte immer wieder angeregt, eingefordert und geübt werden. Eine sinnvolle Unterstützung kann hierbei eine schriftliche Anleitung für die Partnerarbeit sein, bei der ein Sprachmuster vorgegeben sind.
Abbildung 3
Eine alternative Möglichkeit besteht darin, den Kindern mehrere Streifen mit jeweils 6 abgebildeten Punkten zur Verfügung zu stellen und diese knicken bzw. falten oder zerschneiden zu lassen.
Anschließend werden die „zerlegten“ Streifen gelegt (aufgeklebt), die Schnittkante bzw. Faltkante wird markiert und die Zerlegungen werden benannt.
Abbildung 4
Die Kinder sollten zudem angeregt werden, die gefundenen Zerlegungen zu dokumentieren. Hier gibt es verschiedene Möglichkeiten, durch die zugleich auch verschiedene Darstellungsebenen miteinander verknüpft werden können (vgl. auch "Dokumentation der Zerlegungen“ und "Verknüpfen verschiedener Zerlegungsdarstellungen“ unter Reduktion):
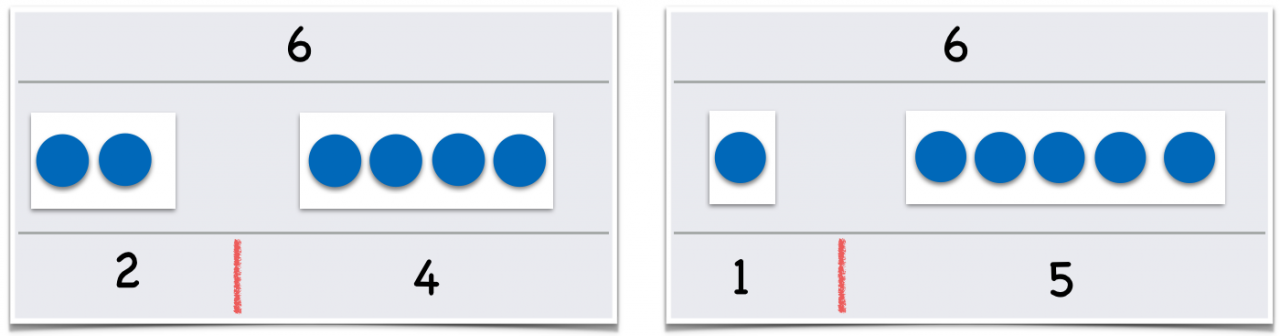Abbildung 5
Wichtig:
Im Vorfeld muss die (mathematische) Bedeutung des Begriffes "Zerlegung" sowie der Zusammenhang von "Zerlegung" und "Teil-Ganzes-Beziehung" mit den Kindern geklärt werden. Ausgehend von der alltagssprachlichen Verwendung des Begriffes (z.B.: "Ich zerlege eine ganze Tafel Schokolade in mehrere Teile") wird die Bedeutung des "Zerlegens einer Zahl" in den Blick genommen:
"Ich zerlege 6 in 4 und 2."
("Ich zerlege eine Menge von 6 Plättchen in die Teilmengen 4 Plättchen und 2 Plättchen.")
Beachtet werden muss zudem, dass mit dem Begriff "Zerlegung" im Allgemeinen die "Zerlegung in zwei Teilmengen" assoziiert wird. Gleichwohl ist natürlich immer auch eine Zerlegung in drei oder mehr Teilmengen denkbar (vgl. hierzu auch die Aufgabe "Zerlegen von Zahlen in drei (oder mehr) Teile" unter Erweiterung).
Weitere Informationen und Anregungen zur Arbeit mit Kindern, die einen Unterstützungsbedarf im Bereich Sprache haben, finden Sie in der Rubrik Förderschwerpunkte: Sprache.
Vertiefende Hinweise zur Sprachförderung im Mathematikunterricht erhalten Sie auch auf der Webseite unseres Partnerprojektes primakom: Vielfalt – Sprachförderung – Einstieg.
Vertiefung
Dokumentation der Zerlegungen
Material: AB, Papierstreifen zur Notation, Papierstreifen mit 6 Punkten
Eine vertiefende Aktivität besteht in der Dokumentation der gefundenen Zerlegungen.
Hier gibt es verschiedene Möglichkeiten:
Zum einen kann eine tabellarische Übersicht erstellt werden. Die Kinder zeichnen die Zerlegungen ein und notieren die entsprechenden Zahlen. Einige Kinder werden bei der Dokumentation der Zerlegungen bereits systematisch vorgehen und die Zerlegungen geordnet notieren. Andere Kinder ordnen die Zerlegungen im Anschluss an die Dokumentation. Damit die Zerlegungen geordnet werden können (vgl. "Sortieren und Ordnen der gefundenen Zerlegungen"), kann die Übersicht zerschnitten werden.
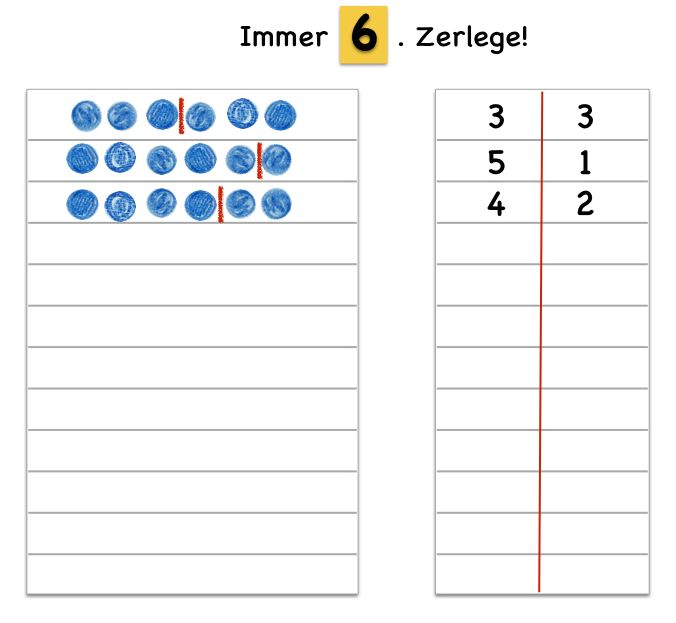Abbildung 6
Alternativ können die Zerlegungen auch direkt auf Papierstreifen gezeichnet werden:
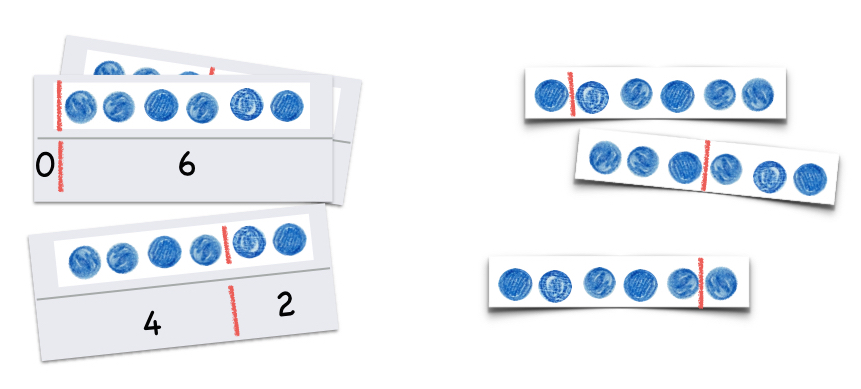Abbildung 7
Eine weitere Möglichkeit besteht darin, den Kindern Papierstreifen mit 6 linear angeordneten Punkten zur Verfügung zu stellen, bei denen dann nur noch ein Trennstrich zwischen die Teilmengen gezeichnet wird:
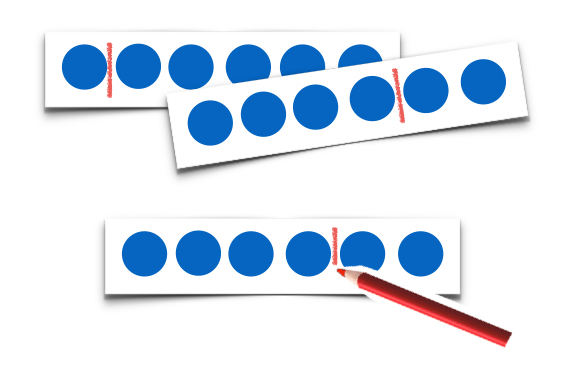Abbildung 8
Neben der zeichnerischen / ikonischen Dokumentation der Zerlegungen gibt es verschiedene Möglichkeiten, die Zerlegungen mit Zahlen zu bezeichnen und auf der symbolischen Ebene zu dokumentieren (vgl. auch die tabellarische Übersicht oben):
Abbildung 9
Vertiefung
Sortieren und Ordnen der gefundenen Zerlegungen
Material: Sortiertafel / Dokumentationen der gefundenen Zerlegungen
Die gefundenen Zerlegungen zu sortieren und zu ordnen ist eine weitere wichtige Aktivität. Hier sind verschiedene Ordnungen möglich. Die Kinder können sich beim Ordnen der Zerlegungen sowohl an der Plättchendarstellung als auch an den notierten Additionsaufgaben orientieren. Denkbar ist eine Ordnung, bei der Bezug auf die (aufsteigende bzw. absteigende) Zahlenfolge genommen wird oder bei der die Plättchendarstellungen als Muster angeordnet werden.
Ziel des Ordnens ist es, ein über die einzelnen Zerlegungen hinausgehendes Muster zu erkennen und die Struktur zu beschreiben.
Beispiel 1: Wird der Stift ein Plättchen (z.B. nach links) weitergelegt, erhöht sich die rechte Teilmenge der Plättchen um eins und die linke Teilmenge der blauen Plättchen vermindert sich um eins. Die Gesamtmenge der Plättchen bleibt gleich („gegensinniges Verändern“).
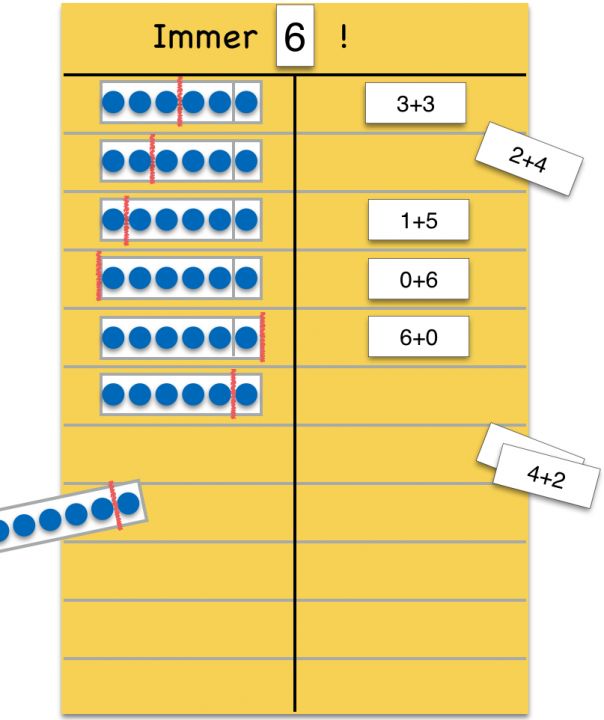Abbildung 10
Beispiel 2: Hier wird immer eine Aufgabe mit der jeweiligen Tauschaufgabe kombiniert. Dabei wird zugleich (immer bezogen auf das nächste Paar) der erste Summand um eins vermindert.
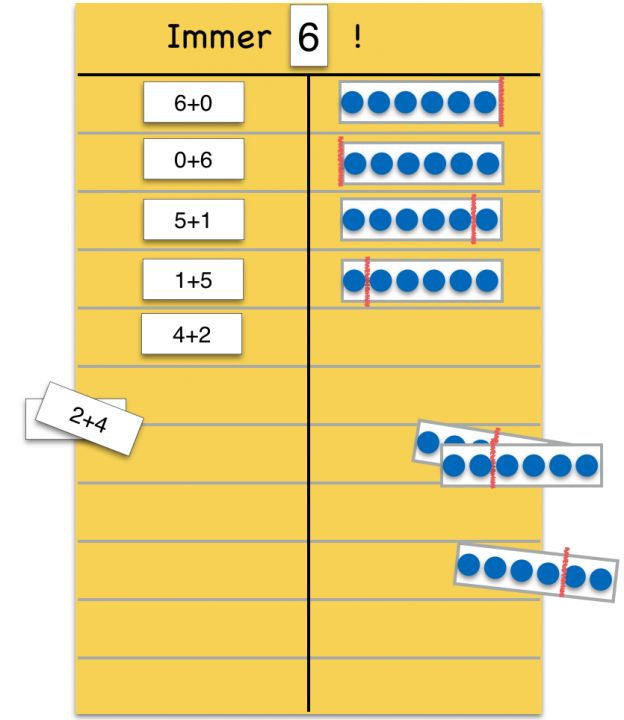Abbildung 11
Beispiel 3: Der erste Summand wird immer um eins vermindert (bezogen auf die nächste Aufgabenkarte), der Stift wird immer um ein Plättchen nach links verschoben. Zugleich erhöht sich der zweite Summand um eins.
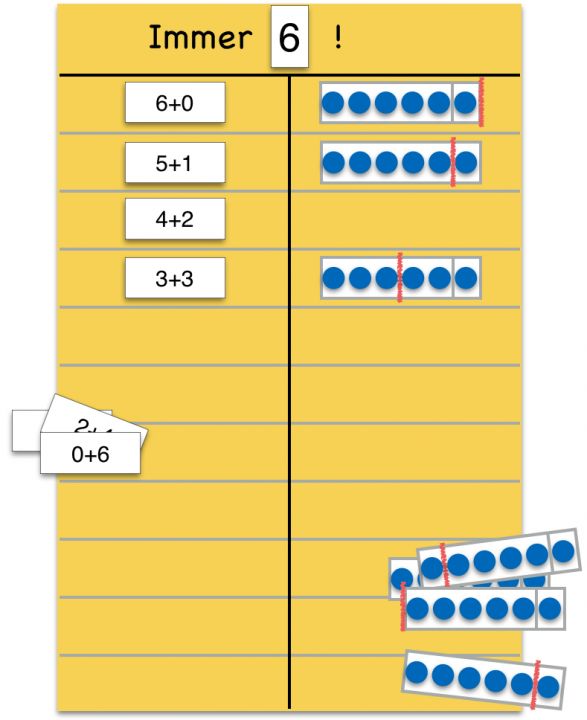Abbildung 12
Vertiefung
Beschreiben und Begründen der Anordnungen
Material: Sortiertafeln mit geordneten Zerlegungen
Wesentlich ist auch das Beschreiben und Begründen der Anordnungen. Die Kinder beschreiben jeweils die von ihnen vorgenommene Ordnung und vergleichen diese mit den Ordnungen der anderen Kinder.
Hierbei können Ordnungssysteme verglichen sowie fehlende Zerlegungen gefunden und ergänzt werden.
Gleichzeitig geht es um die Frage, ob alle Zerlegungen gefunden wurden, wie (systematisch) vorgegangen werden kann, damit alle Zerlegungen gefunden werden bzw. wo man direkt erkennen kann, ob alle möglichen Zerlegungen notiert wurden:
„David hat die Zerlegungen anders geordnet als Paula! Was ist anders? Erklär mal!“
„Vergleiche die Ordnung von David und die Ordnung von Paula! Was fällt dir auf?“
„Sind das alle Möglichkeiten / Zerlegungen? Woher weißt du das?“
„Wie kannst du überprüfen, ob du alle Zerlegungen gefunden hast?“
„Wie kannst du schnell erkennen, ob du alle Zerlegungen gefunden hast?“
„Wie kannst du vorgehen, damit du sicher alle Zerlegungen findest?"
Vertiefung
Verknüpfen von Zerlegungsdarstellungen
Material: Vorlage zum Zuordnen / verschiedene Darstellungen von Zerlegungen
Die Kinder erhalten verschiedene Darstellungen von Zerlegungen (Plättchendarstellungen / symbolische Darstellungen / Fingerbilder / …) und ordnen Darstellungen auf einer Vorlage zum Zuordnen einander zu.
Der Fokus liegt hier auf der Verknüpfung bzw. Zuordnung von Repräsentanten einer Darstellungsebene bzw. zwischen Darstellungsebenen und dem Bestimmen der Teilsummanden. Variiert werden können hier - je nach Zielsetzung und den jeweiligen Lernvoraussetzungen der Kinder - die Darstellungen und die Anzahl der Darstellungen, die den Kindern zur Verfügung gestellt werden. Wobei der Schwerpunkt dieser Aufgabenstellung - im Sinne einer Vertiefung der Basisaufgabe - in der Verknüpfung von symbolischen und ikonischen Darstellungen liegen sollte.
Erfolgt der Zugang zur Zahlzerlegung bei einem Kind über Fingerbilder, sollten diese zusätzlich einbezogen werden. Hier bieten sich dann fokussierte Zuordnungsübungen an, bei denen der Schwerpunkt beispielsweise auf der Verknüpfung von Fingerbildern und Plättchendarstellungen liegt (vgl. hierzu die Aufgabe "Verknüpfung ausgewählter Zerlegungsdarstellungen" unter Reduktion).
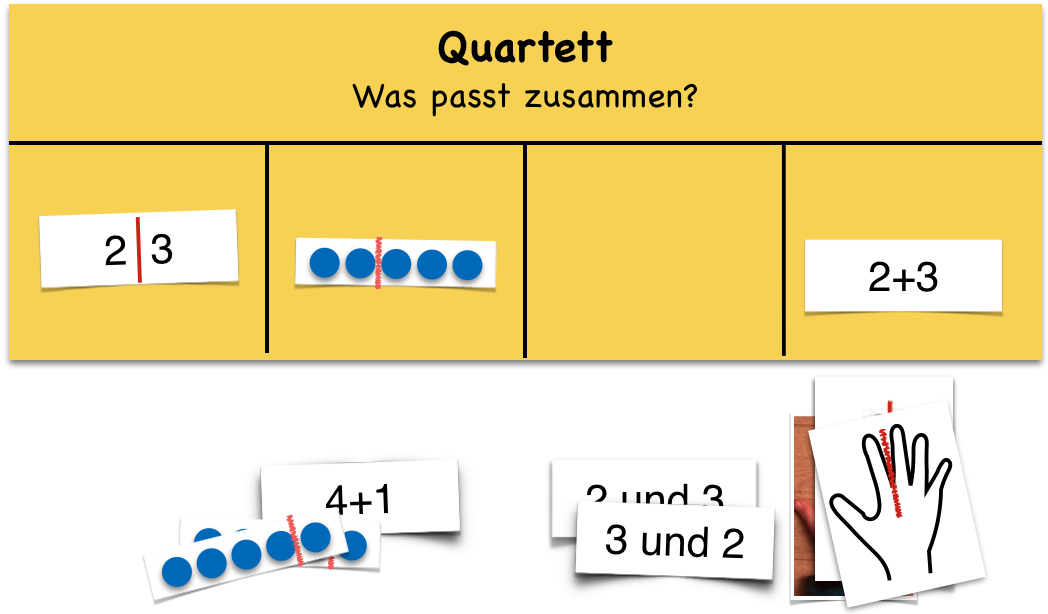Abbildung 13
Gleichzeitig können die Zuordnungen sprachlich begleitet und begründet werden, z.B.:
„Die Karten passen zueinander. Auf der einen Karte sind 5 Plättchen, zerlegt in 2 (Plättchen) und 3 (Plättchen) und auf der anderen Karte steht 2 und 3.“
Alternativ kann mit den verschiedenen Zerlegungsdarstellungen wie mit Spielkarten in einem Quartettspiel gespielt werden.
Reduktion
Zerlegen 'kleinerer' Zahlen (2; 3; 4; 5)
Material: Plättchen, Legerahmen, Stift, Papierstreifen mit abgebildeten Punkten
Die Kinder zerlegen – analog zur Basisaufgabe - die in einer Reihe angeordneten Plättchen (2; 3; 4; 5) mit einem Stift in zwei Teile oder zerschneiden die Streifen und benennen die gefundenen Zerlegungen. Wird mit kleineren Zahlen gearbeitet, reduziert sich die Anzahl möglicher Zerlegungen.
Reduktion
Fokussierung auf die Zerlegungen der Zahlen 5 und 10
Material: Plättchen, Legerahmen, Stift, Papierstreifen mit abgebildeten Punkten
Obwohl sicher die Kenntnis aller Zerlegungen der Zahlen von 1 bis 10 für den Aufbau und das Nutzen operativer bzw. heuristischer Strategien von grundlegender Bedeutung ist, nehmen die Zerlegungen der Zahlen 5 und 10 (20) hier doch eine besondere Rolle ein. „Grundsätzlich sind die Zerlegungen der Zahlen von 5, 10, 20 […] besonders wichtig und müssen daher intensiv eingeübt werden“ (Km Bayern 2012, 210; vgl. auch Hasemann & Gasteiger 2014, 159).
So werden die Zerlegungen der 10 bei jeder Additions- und Subtraktionsaufgabe mit Zehnerübergang benötigt. Beherrschen die Kinder die Zerlegungen der Zahl 5, können diese bei der Erarbeitung der Zerlegungen der Zahl 10 eine Hilfe sein wie z.B.:
5 = 2 + 3 und 10 = 5 + 2 + 3
Abbildung 14
Reduktion
Fokussierung auf das Zerlegen der Plättchendarstellung
Material: Plättchen, Legerahmen, Stift, Papierstreifen mit abgebildeten Punkten
In der Partnerarbeit zerlegt ein Kind die Plättchendarstellung. Die Bezeichnung der Teilmengen mit Zahlen wird dann von dem jeweiligen Partnerkind übernommen. Anschließend wiederholt das Kind, das die Plättchendarstellung zerlegt hat, die Bezeichnung der Teilmengen.
Eine weitere mögliche Variation der Aufgabenstellung besteht darin, nach der Zerlegung der Plättchendarstellung die Teilmengen zunächst miteinander zu vergleichen: Ein Kind beschreibt, welche der beiden Teilmengen mehr / weniger Plättchen enthält bzw. ob in beiden Teilmengen gleich viele Plättchen enthalten sind:
„Hier sind mehr / weniger Plättchen.“
„Es sind gleich viele Plättchen.“
Das Partnerkind benennt dann die konkrete Anzahl der Plättchen.
Reduktion
Verknüpfen ausgewählter Zerlegungsdarstellungen
Material: Sortiertafel / verschiedene Darstellungen von Zerlegungen
Während bei der Aufgabenstellung „Verknüpfen verschiedener Zerlegungsdarstellungen“ (vgl. Basisaufgabe und vertiefende Aufgabenstellungen) die Zuordnung symbolischer und ikonischer Zerlegungsdarstellungen im Mittelpunkt steht und zugleich mehrere Darstellungen einander zugeordnet werden sollen, liegt der Schwerpunkt der Aufgabenstellung „Verknüpfen ausgewählter Zerlegungsdarstellungen“ im Bereich Reduktion auf der Zuordnung von jeweils zwei (ausgewählten) Zerlegungsdarstellungen.
Erfolgt beispielsweise der Zugang zur Zahlzerlegung bei einem Kind über Fingerbilder (vgl. hierzu „Zerlegen von Fingerbildern“ unter Möglichkeiten individueller Unterstützung), kann es sinnvoll sein, den Schwerpunkt der Zuordnungsübung auf die Verknüpfung von Fingerbildern und Plättchendarstellungen zu legen.
Da die Arbeit mit Fingerbildern im Allgemeinen auf den Zahlenraum bis 10 begrenzt ist, gilt es, die Zusammenhänge zwischen Fingerbildern und Plättchendarstellungen sichtbar zu machen, um die Ablösung von den Fingerbildern zu ermöglichen und produktiv zu begleiten (vgl. Häsel-Weide 2014, 33).
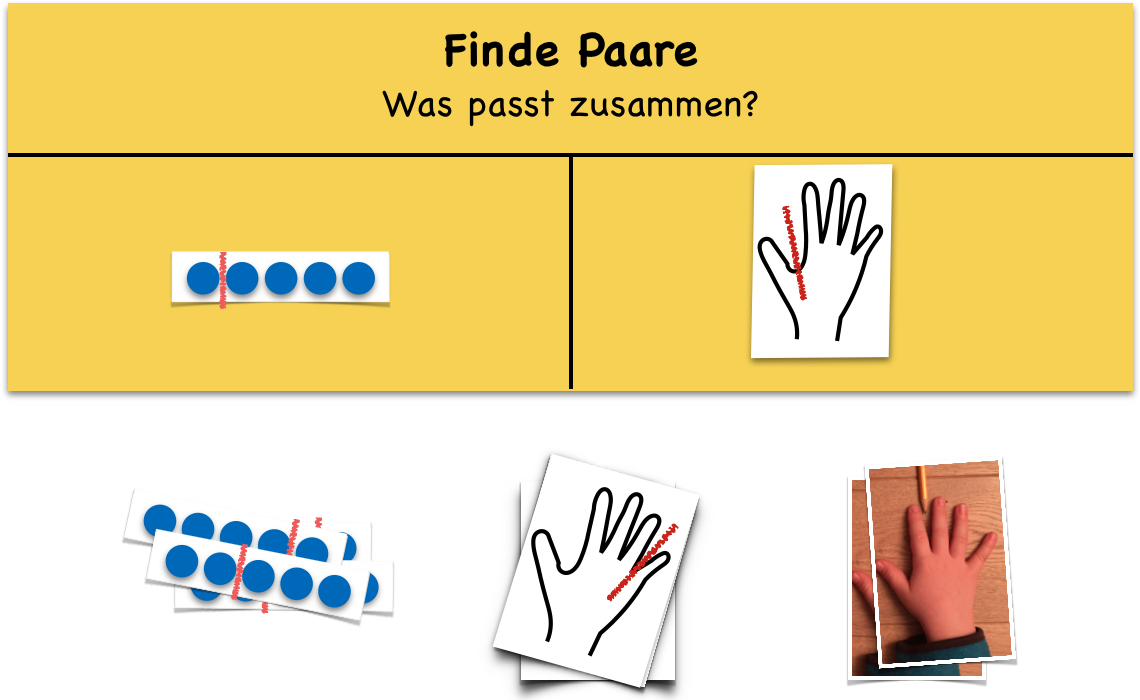Abbildung 15
Alternativ können die verschiedenen Zerlegungsdarstellungen wie Spielkarten in einem Spiel eingesetzt werden, bei dem es um das Finden von zueinander passenden Karten geht („Finde Paare“).
Erweiterung
Zerlegen selbst gewählter 'großer' Zahlen
Material: AB mit leeren Zahlenhäusern
Die Kinder wählen selber Zahlen aus, zu denen sie Zerlegungen finden und in Zahlenhäuser notieren. Je nach ausgewählten Zahlen können die erstellten Zahlenhäuser im Anschluss verglichen und mögliche Analogien entdeckt werden (z.B. Zahlenhäuser zur 6 und 16).
Erweiterung
Vergleichen von Zahlenhäusern
Material: AB mit leeren Zahlenhäusern
Die Kinder notieren die Zahlzerlegungen zu mehreren Zahlen (Nachbarzahlen) systematisch in Zahlenhäusern, vergleichen anschließend die Zahlenhäuser miteinander und notieren bzw. markieren, was ihnen auffällt.
„Vergleiche die Zahlenhäuser. Was fällt dir auf?“
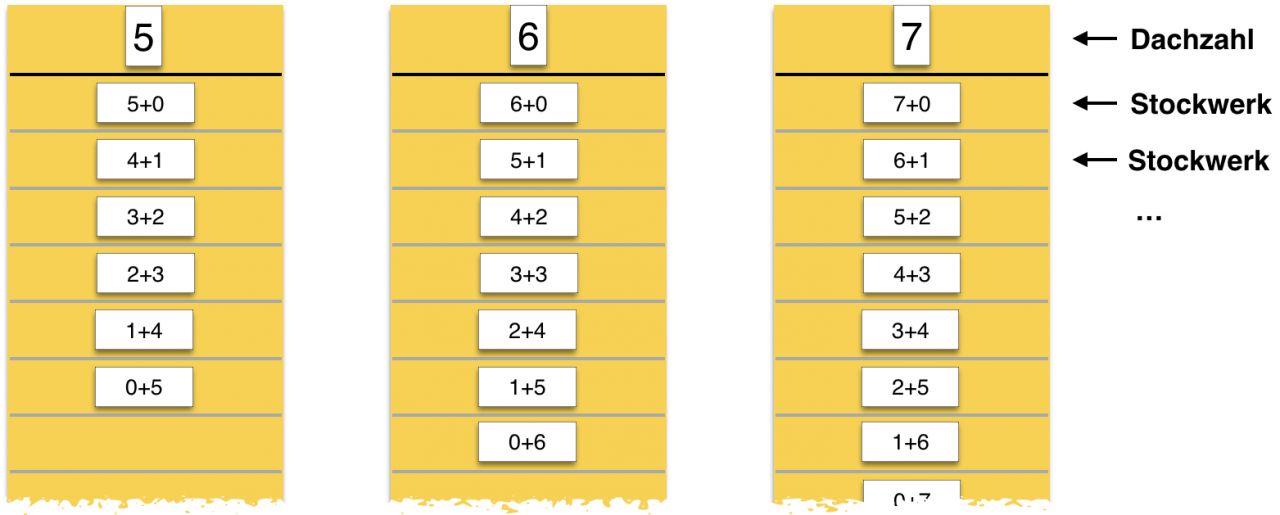Abbildung 16
Mögliche Entdeckungen:
-
Je größer die Dachzahl, desto mehr Stockwerke sind nötig.
-
Bei Häusern mit aufeinander folgenden Dachzahlen (z.B. 5,6,7,8,..) wächst die Anzahl der benötigten Stockwerke jeweils um 1.
-
Die Dachzahl + 1 ergibt jeweils die Anzahl der benötigten Stockwerke.
-
Verdoppelungsaufgaben kommen nur bei geraden Dachzahlen vor.
-
Wenn die Anordnung der Zahlzerlegungen dem obigen Beispiel entspricht: Der zweite Summand ist in den jeweiligen Stockwerken immer gleich.
-
...
Erweiterung
Zerlegen von Zahlen in drei Teile
Material: AB
Die Kinder werden angeregt, eine Zahl (z.B. 6) in drei (oder mehr) Teile zu zerlegen und verschiedene Möglichkeiten zu finden.
Um die Anzahl der möglichen Zerlegungen zu begrenzen, kann es sinnvoll sein, die leere Menge als mögliche Teilmenge auszuschließen und nur Mengen mit mindestens einem Element zuzulassen - zumal es darüber hinaus schwierig ist, Zerlegungen mit leeren Teilmengen an einer Punktereihe mit Stiften darzustellen bzw. durch Zerschneiden herzustellen.
Wird die leere Menge als mögliche Teilmenge zugelassen, ist es angezeigt, die Zerlegung nur auf der symbolischen Ebene durchzuführen. Hier wird die Zerlegung beispielsweise mittels Zahlentripeln oder als Additionsaufgabe dargestellt, die die Anzahl der Elemente in einer Teilmenge bezeichnen. D.h. das Zahlentripel 0 / 0 / 6 entspricht einer Zerlegung in zwei leere Teilmengen und in eine Teilmenge mit 6 Elementen.
"Finde alle (verschiedene) Möglichkeiten. Wie gehst du vor?“
Beispiel mit Angabe der möglichen Zahlzerlegungen.
Zerlegung der Zahl 6 in drei Teile / die leere Menge ist als Teilmenge zugelassen:
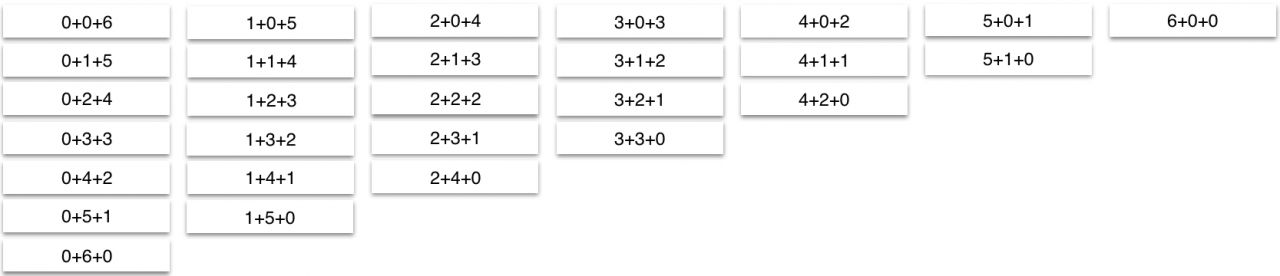Abbildung 17
Beispiel mit Angabe der möglichen Zahlzerlegungen.
Zerlegung der Zahl 6 in drei Teile / die leere Menge ist als Teilmenge nicht zugelassen:
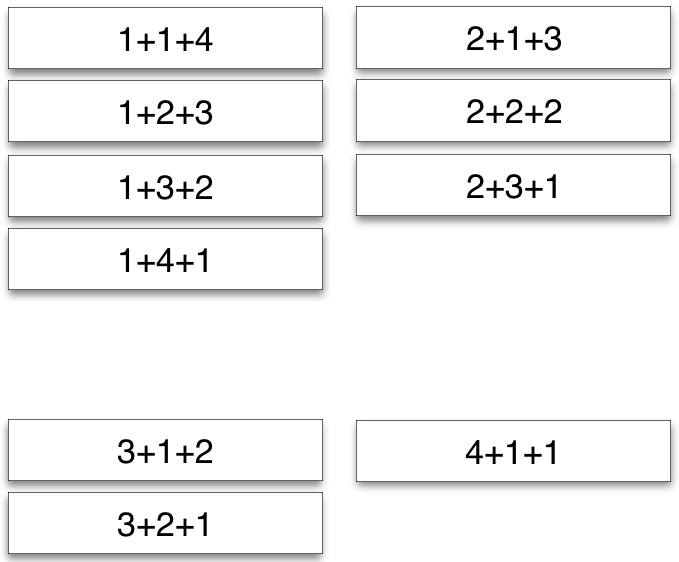Abbildung 18
Erweiterung
Ergänzen von Zahlzerlegungen
Material: Sortiertafel, Papierstreifen mit abgebildeten Punkten, Ergänzungsstreifen, Streifen mit Additionsaufgaben (ein Summand verdeckt)
Die Kinder haben die Aufgabe, unvollständig vorgegebene Zahlzerlegungen zu ergänzen.
Vorgegeben werden Additionsaufgaben, bei denen ein Summand verdeckt ist.
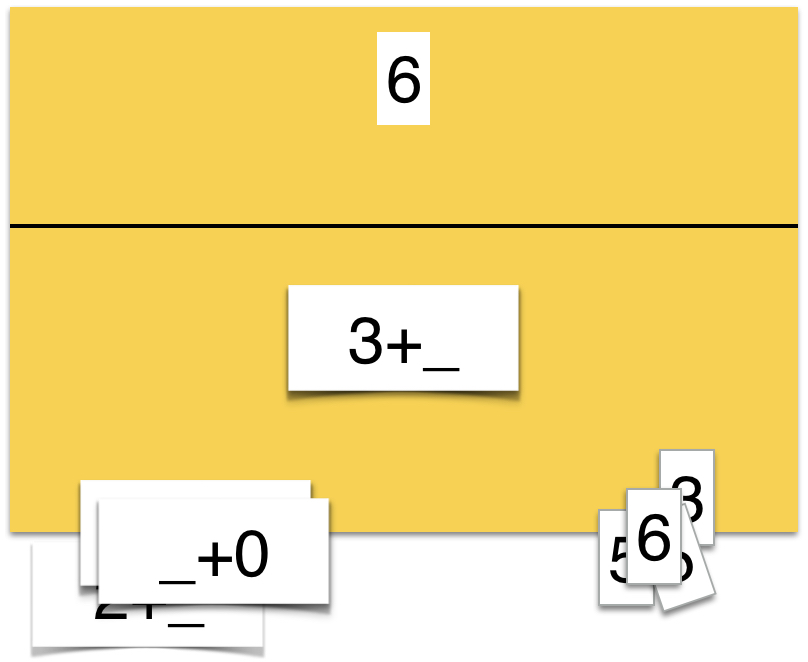Abbildung 19
Bei Bedarf können die Ergänzungen im Anschluss überprüft werden:
Auf bzw. unter eine Darstellung der Gesamtmenge werden die Teilmengen gelegt und die Passung der ergänzten Teilmengen wird kontrolliert.
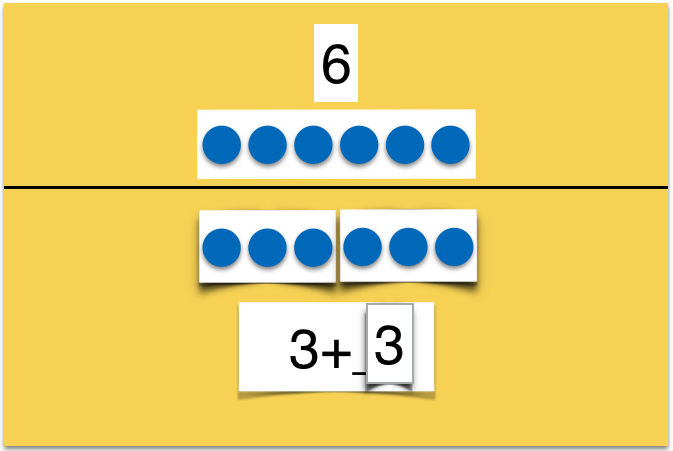Abbildung 20
Erweiterung
Erklärvideos zu Zahlzerlegungen mit der App "Rechenfeld" erstellen
Die Kinder planen und erstellen gemeinsam kurze Erklärvideos zu den Zerlegungen der 6 (5,7). Dazu kann beispielsweise die App „Rechenfeld“ genutzt werden. Mittels Bildschirm- und Tonaufnahmen können (Lege-)Handlungen mit Plättchen aufgezeichnet und von den Kindern in dem Video sprachlich erklärt werden. Eine beispielhafte Schülerlösung zur Fragestellung "Wie kannst du vorgehen, damit du sicher alle Zerlegungen findest?" finden Sie im untenstehenden Erklärvideo von Kindern einer ersten Klasse.
Einblicke in die App "Rechenfeld" (C. Urff)
Die entstandenen Videos können im Nachhinein erneut betrachtet und reflektiert werden, z. B. mithilfe von Reflexionsfragen wie „Wurden alle Zerlegungen gefunden? Warum?“, „Wie haben die Kinder alle Zerlegungen gefunden?“, „Welche Zerlegungen gibt es noch?“.
Auch kann reflexiv ein allgemeinerer Fokus auf Kriterien gelungener und weniger gelungener Erklärungen gelegt werden. Mögliche Reflexionsfragen für das gemeinsame Betrachten der Videos in Kleingruppen oder der Klasse wären: „Habt ihr die Erklärung verstanden?", „Würde ein Kind aus einer anderen Klasse die Erklärung auch verstehen?", „Welche Begriffe aus dem Wortspeicher hätten unsere Erklärung noch verständlicher gemacht?", „Was könnten wir bei der Erstellung eines neuen Erklärvideos noch besser machen?", „Was hat euch gut gefallen?".
Die Erstellung der Erklärvideos durch die Kinder verfolgt nicht das Ziel, dass „ideale“ Videos entstehen, sondern dass sich die Kinder im Vorhinein Gedanken um die sprachliche Begleitung der Handlungen machen und diese im Nachgang durch ein erneutes Anschauen reflektieren können.
Möglichkeiten individueller Unterstützung
Legen der Zahldarstellungen
Zum Legen der Zahldarstellungen (z. B. 6 linear angeordnete Wendeplättchen) können statt Wendeplättchen auch „Wendesteine“ (Rechenschiffchen) verwendet werden. Das Verrutschen der Wendesteine kann beispielsweise durch den Einsatz einer Filzunterlage verhindert werden.
Abbildung 21
Möglichkeiten individueller Unterstützung
Zur kognitiven Entlastung die App „Rechentablett“ nutzen.
Als Alternative zu Wendeplättchen kann die App „Rechentablett“ (Informationen zu der App finden Sie bei PIKAS digi und unter Lernsoftware Mathematik) genutzt werden, um die Zahlzerlegungen zu erkunden. Hierzu wird eine beliebige Anzahl an Plättchen gelegt und anschließend kann durch Verschieben der Plättchen die Zerlegung erkundet werden.
Einblicke in die App "Rechentablett" (C. Urff)
Möglichkeiten zur Reduktion bietet die App, indem beispielsweise auf die symbolische Notationsform verzichtet und zunächst nur die Darstellung mit Plättchen genutzt werden kann. Das automatisierte Berechnen der Menge kann im größeren Zahlenraum auch unterstützend eingesetzt werden, wenn die Kinder sich auf die Veränderungen der Plättchen konzentrieren können und das kognitive Arbeitsgedächtnis entlastet werden kann. Erweiternd kann in den Einstellungen der App der Zahlenraum beliebig vergrößert werden.
Möglichkeiten individueller Unterstützung
Dokumentieren der Zahlzerlegungen
Statt die Zahlzerlegungen zu zeichnen, können die Kinder die Zahlzerlegungen auch mit einem Stempel dokumentieren.
Material (Stempel): Kreis aus Moosgummi (in Plättchengröße) / Flaschenkorken / doppelseitiges Klebeband
Abbildung 22
Möglichkeiten individueller Unterstützung
Beschreiben und Begründen der Anordnungen und Sortierungen
Wichtig ist es zunächst, das Sprachverständnis der Kinder zu sichern, d.h. die alltagssprachliche Bedeutung und die mathematische Bedeutung des Begriffes „zerlegen“ mit den Kindern zu klären (vgl. die Erläuterungen zur Basisaufgabe). D.h. die Kinder müssen eine Vorstellung davon entwickeln was es heißt, Zahlen zu zerlegen.
Zur Beschreibung der Muster und zum Begründen der Anordnungen und Sortierungen können die Kinder Sprachmuster verwenden und einen Wortspeicher anlegen. Mögliche Begriffe für den Wortspeicher:
Zerlegung / zerlegen / 1. Zahl / 2. Zahl / rechts (vom Stift) / links (vom Stift) / zerschneiden / mehr / weniger / gleich / ….
Der Einsatz von Sprachmustern und Textbausteinen unterstützt die Kinder beim Beschreiben, Begründen und beim Übertragen des Sachverhaltes auf andere Situationen:
… wird zerlegt in … und … / Ich zerlege … Plättchen in … und in … Plättchen / Du zerlegst … Plättchen in … und in … Plättchen / Der erste Summand wird um … mehr / weniger / ...
Weitere Informationen und Anregungen zur Arbeit mit Kindern, die einen Unterstützungsbedarf im Bereich Sprache haben, finden Sie in der Rubrik Förderschwerpunkte: Sprache.
Möglichkeiten individueller Unterstützung
Fokussieren von Teilmengen
Zur Fokussierung und zum Hervorheben von Teilmengen der Zahldarstellungen können farbige Folien (transparent) eingesetzt werden.
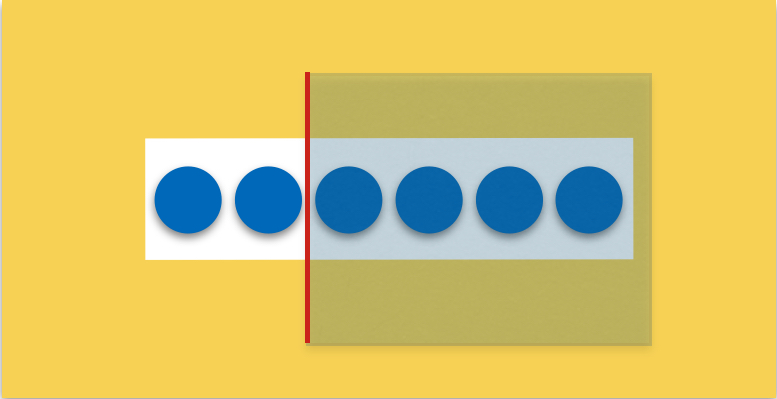Abbildung 23
Möglichkeiten individueller Unterstützung
Zerlegen von Fingerbildern
Anstelle der Plättchen können - für die Zerlegung der 5 und der 10 - auch Fingerbilder eingesetzt und zerlegt werden, indem ein Stift zwischen die Finger gehalten wird. Die Arbeit an und mit Fingerbildern kann (muss aber nicht) für Kinder eine Hilfe sein. „Punktedarstellungen werden nur über die Augen wahrgenommen – im Unterschied zu Fingerdarstellungen, die auch über den eigenen Körpersinn erfahren werden“ (Gaidoschik 2007, 54).
Die Dokumentation erfolgt dann über das Einzeichnen von Strichen in vorgegebene Fingerbilder.
Abbildung 24
Achtung! Wird mit den Fingern gearbeitet, muss immer darauf geachtet werden, dass diese ausschließlich statisch (als Fingerbild) eingesetzt werden.
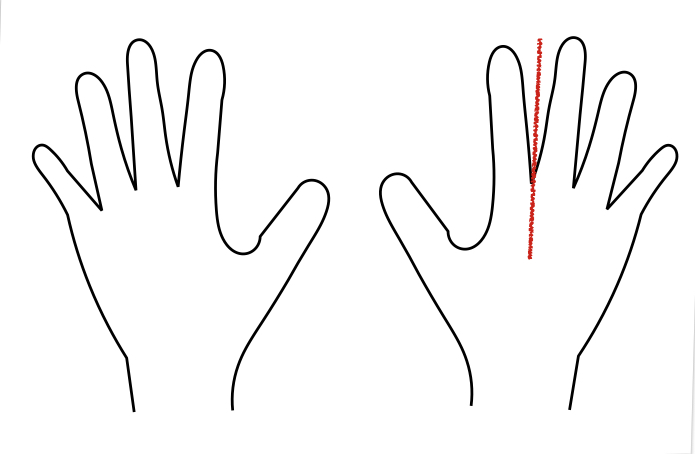Abbildung 25
Beachtet werden sollte aber, dass die Arbeit mit Fingerbildern im Zahlenraum bis 10 durchaus sinnvoll, aber darüber hinaus kaum fortsetzbar ist. Wichtig ist deshalb auch, die Ablösung von den Fingerdarstellungen anzustreben und produktiv zu begleiten (vgl. Häsel-Weide 2014, 33).
