Gemeinsames Lernen mit Hilfe von Tipps und Herausforderungen
– Das Erforschen operativer Veränderungen an Zahlenmauern auf Grundlage unterstützender und weiterführender Aufgabenstellungen
Ein konkretes Beispiel für Aufgaben, bei denen sich „Tipps und Herausforderungen“ gut eignen, entstammt einer Unterrichtsreihe zum Thema „Zahlenmauern“. „Zahlenmauern“ sind ein strukturiertes Übungsformat und eine bewährte Übungsform, die zahlreiche operative Variationen und eine Vielzahl von produktiven Übungen ermöglichen (vgl. Müller & Wittmann, 2012). Aufgrund der vielfältigen Variationsmöglichkeiten (Zahlenräume, Höhen der Mauern etc.), sind Aufgabenstellungen für jedes Leistungsniveau herstellbar (vgl. Nührenbörger & Pust, 2011). Das Aufgabenformat ist zudem im Sinne des Spiralprinzips (vgl. Krauthausen & Scherer, 2008) in darauffolgenden Schuljahren sinnvoll weiterführbar.
Dem Format liegt folgende Rechenvorschrift zugrunde:
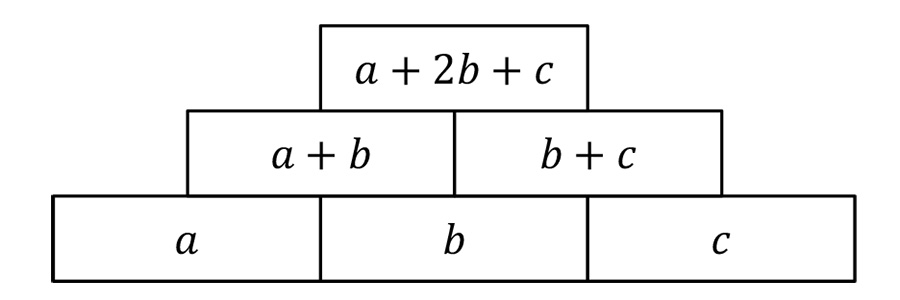 Abbildung 3: 3er-Zahlenmauer
Abbildung 3: 3er-Zahlenmauer
Eine 3er-Zahlenmauer (Abb. 3) setzt sich aus drei Grundsteinen (a, b, c mit a, b, c ≥ 0) zusammen. Die Summe zweier benachbarter Steine ergibt den Wert des darüber liegenden Steines. Das Erkennen dieses mathematischen Musters ist der Hauptschwerpunkt einer Unterrichtsreihe, bei der die Problemlösefähigkeit der Kinder gefördert werden soll, indem sie verstehen sollen, wie sich operative Veränderungen der Grundsteine auf den Deckstein auswirken. Wird der linke Eckstein a einer 3er-Zahlenmauer beispielsweise um 1 (2, 3, …) erhöht, so erhöht sich der Deckstein (a+2b+c) auch um 1 (2, 3, …). Erhöht man jedoch den Mittelstein b um 1 (2, 3, …), so erhöht sich der Deckstein (a+2b+c) um 2 (4, 6, …).
Die hier gezeigten Kinderdokumente entstammen der Unterrichtsstunde, in der das Kernanliegen (der initiierte/bewusste Lernzuwachs am Ende der geplanten Unterrichtsstunde) darin besteht, festzustellen, dass eine Erhöhung des Mittelsteins b um n, eine Erhöhung des Decksteins (a+2b+c) um 2n nach sich zieht.
Wie kann man diesen komplexen Sachverhalt für Kinder unterschiedlicher Leistungsniveaus erfahrbar machen? Der Schlüssel liegt bereits in der Aufgabenwahl der Basisstufe. Hier sind Aufgaben bzw. Aufgabenformate zu wählen, welche mit einfachen Mitteln auf variierte Aufgabenstellungen der Unterstützungs- oder Erweiterungsstufen adaptierbar sind. Durch leichte Veränderungen der Aufgabenstellung wird demnach allen Kindern ermöglicht, Erkenntnisse zu gewinnen, die zum Erreichen des Kernanliegens benötigt werden.
Das folgende Beispiel entstammt einer Unterrichtsreihe, die in einer aus 30 Schülerinnen und Schülern bestehenden zweiten Schulklasse mit sehr heterogenen Lernvoraussetzungen durchgeführt wurde. In der inklusiven Lerngruppe befinden sich u.a. Kinder mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ und sonderpädagogischem Unterstützungsbedarf im „sozial-emotionalen Bereich“ sowie im Bereich „Sprache“.
Basis
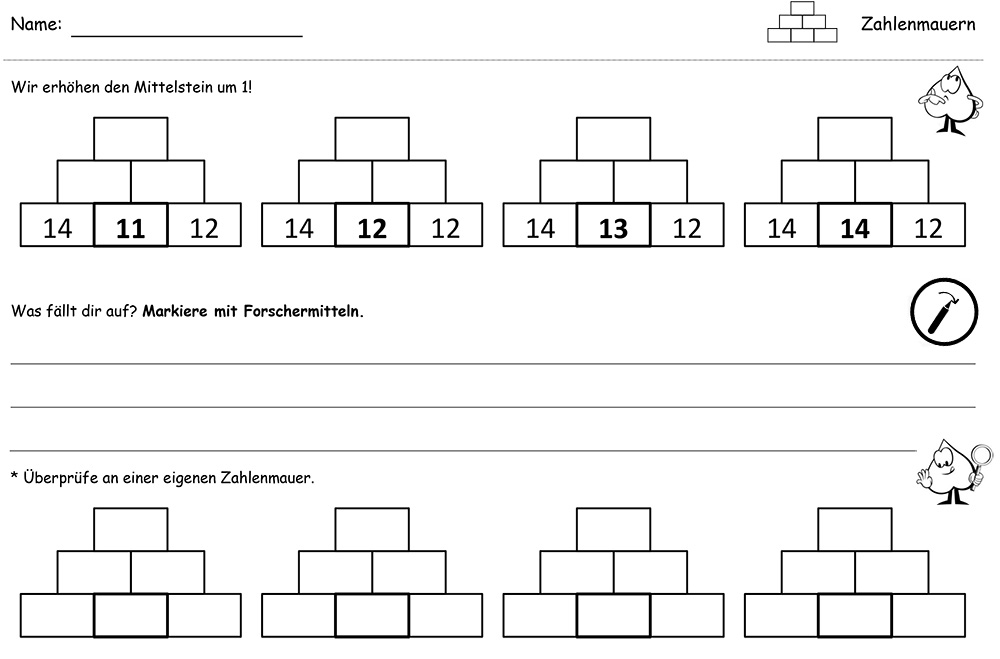 Abbildung 4: Arbeitsblatt „Wir erhöhen den Mittelstein um 1“
Abbildung 4: Arbeitsblatt „Wir erhöhen den Mittelstein um 1“
Das Arbeitsblatt der Basisstufe (vgl. Arbeitsblatt „Wir erhöhen den Mittelstein um 1“) zeigt vier Zahlenmauern im Zahlenraum bis 100, dessen Mittelstein jeweils um eins erhöht ist. Die Kinder sollen die Zahlenmauern berechnen und anschließend ihre gemachten Entdeckungen auf dem Arbeitsblatt verbal oder nonverbal festhalten. Anschließend dürfen sie ihre Vermutungen an einer eigenen Zahlenmauer überprüfen. Eine beispielhafte Bearbeitung des Grundanforderungsblattes zeigt Abb. 5.
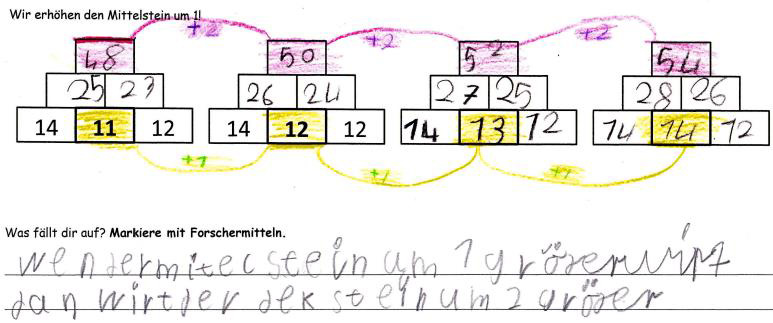 Abbildung 5
Abbildung 5
Die Arbeitsblätter der Erweiterungs- und Unterstützungsstufen greifen diesen Sachverhalt auf, variieren aber in der Formulierung der Aufgabenstellung oder der Komplexität der Zahlenmauern.
Unterstützungsmöglichkeiten
Unterstützung durch Verringerung des Zahlenraumes und/oder Tippkarten
Das Arbeitsblatt (Abb. 6) beinhaltet die gleiche Aufgabenstellung, jedoch ist der Zahlenraum so verringert, dass der Wert des Decksteins im Zahlenraum unter 20 liegt. Die Grundsteine sind analog zu den Zahlen des Grundanforderungsarbeitsblattes (14, 11, 12) gewählt (vgl. ‚Verwandte Aufgaben‘). Leistungsschwächere Kinder, die mit dem Rechnen im Zahlenraum bis 100 noch Probleme haben, können trotzdem erkennen, dass sich der Deckstein um zwei erhöht. Dies ermöglicht es ihnen, ihre Entdeckungen problemlos mit den anderen Kindern in der Reflexionsphase auszutauschen. Haben die Kinder trotz korrekter Berechnung aller Zahlenmauern keine Auffälligkeiten festgestellt, können ihnen Tippkarten (vgl. Tippkarten „Zahlenmauern“) weiterhelfen, die sie dazu auffordern die Mittelsteine und Decksteine miteinander zu vergleichen.
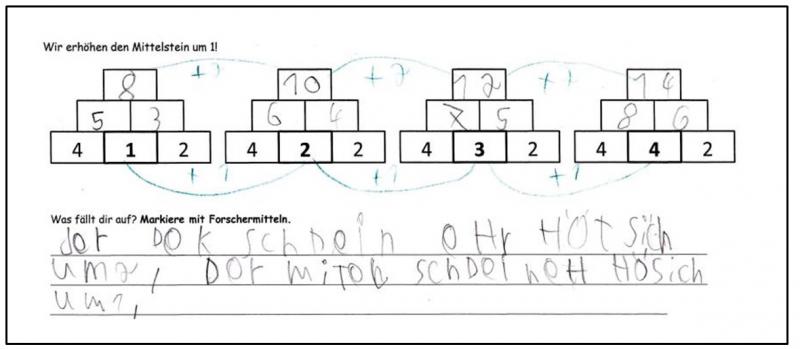 Abbildung 6
Abbildung 6
Unterstützung durch Wortspeicher und Satzbausteine
Die Lernenden können dabei unterstützt werden, Fachwörter und Redemittel zur mündlichen oder schriftsprachlichen Darstellung von Lösungen zu nutzen. Diese Unterstützung ist für alle Kinder der Klasse sinnvoll, ganz besonders aber für Lernende mit dem Förderschwerpunkt Sprache oder Lernende, die Deutsch als Zweitsprache sprechen. „Durch die kontinuierliche Verwendung, Wiederholung und Ausdifferenzierung werden die Ausdrücke fest im Langezeitgedächtnis der Kinder verankert und zunehmend selbstverständlicher genutzt“ (Götze & Hang, 2017, 5). Hierfür empfiehlt sich insbesondere die gemeinsame Erarbeitung eines Klassenwortspeichers, in dem Fachwörter visualisiert und strukturiert festgehalten werden (Götze, 2015). Zum Aufgabenformat „Zahlenmauern“ findet sich ein fertiger Wortspeicher beispielsweise im Zahlenmauern-Übungsheft von PIKAS (Abb. 7).
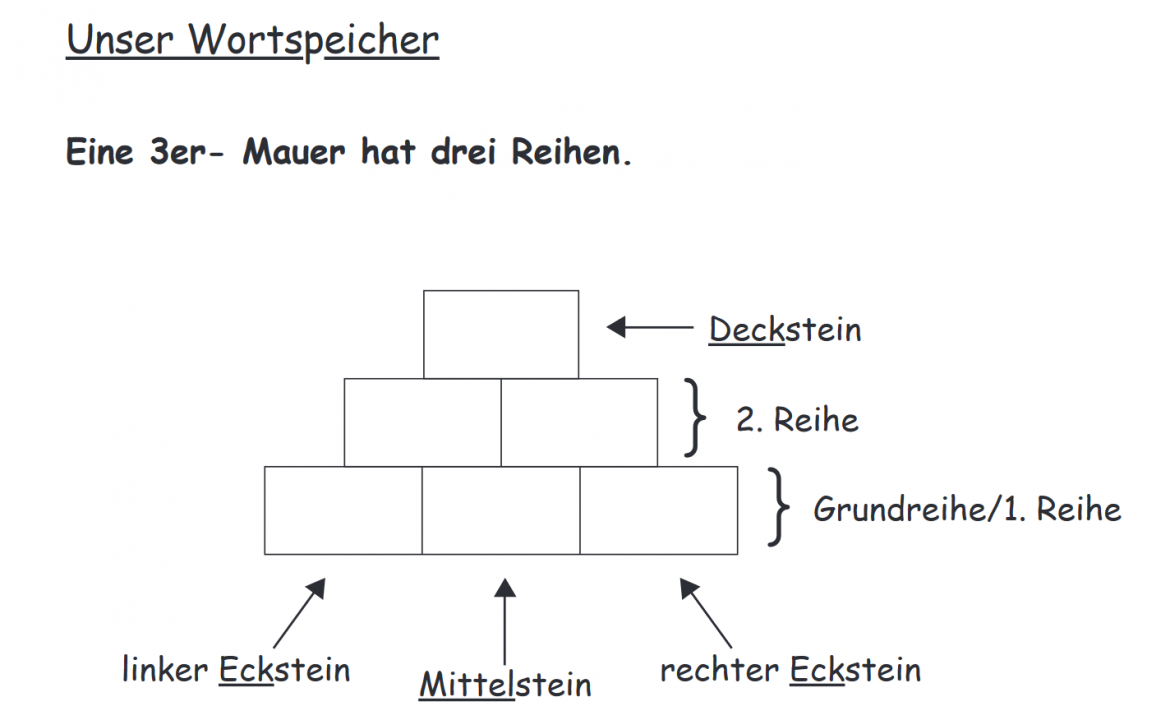 Abbildung 7
Abbildung 7
Unterstützung durch gelöste Aufgaben
Für Kinder mit Unterstützungsbedarf, die auch mit dem Rechnen im Zahlenraum bis 20 Probleme haben, besteht die Möglichkeit, das Arbeitsblatt in gelöster Form anzubieten. So können auch diese Schülerinnen und Schüler dieselben Entdeckungen machen, ohne dass sie an der Hürde des Ausrechnens scheitern und keine Chance haben, das Kernanliegen zu erreichen. Verglichen mit dem bearbeiteten Grundanforderungsarbeitsblatt (Abb. 4) fällt auf, dass auch die Kinder mit Unterstützungsbedarf durch die adaptierten Aufgaben und Tipps (Abb. 8; Abb. 9) dazu in der Lage waren, eine kontinuierliche Erhöhung des Mittelsteins um eins und als Folge die Erhöhung des Decksteins um zwei zu erkennen. Auch wenn die Entdeckung oder Beschreibung auf einem anderen Niveau stattfand, waren der Schüler mit Förderschwerpunkt Lernen (Abb. 8) und die Schülerin mit Förderschwerpunkt Sprache (Abb. 9) dennoch in der Lage an der sich anschließenden Reflexionsphase aktiv teilzunehmen.
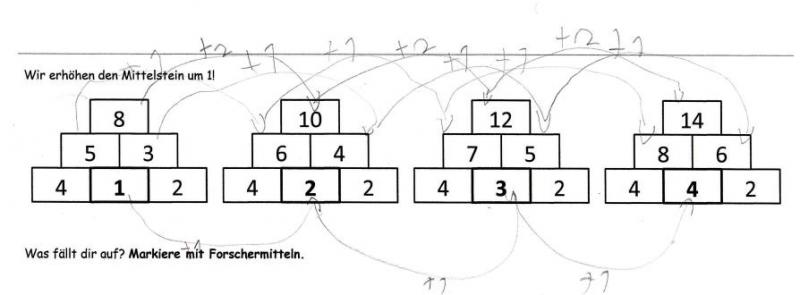 Abbildung 8
Abbildung 8
![Aufgabe „Was fällt dir auf? Markiere mit Forschermitteln.“ Antwort: „Der Deckstein [erhöht sich] um 2“ (Rechtschreibung angepasst).](/pikasmifiles/uploads/Leitideen/Aufgaben-adaptieren/tm2-tipps-unterricht-03-zm_loesung4.jpg) Abbildung 9
Abbildung 9
Erweiterungsmöglichkeiten
Erweiterung durch eigenständige Erhöhung des Mittelsteins um n
Eine Möglichkeit, das Grundanforderungsarbeitsblatt zu erweitern, ist das Erhöhen des Mittelsteins um 2, 3, …n. So können die Lernenden überprüfen, ob ihre Vermutungen auch auf andere Erhöhungen zutreffen und die Regelmäßigkeit erkennen, dass der Deckstein immer um das Doppelte erhöht wird. Auch hier entstand im durchgeführten Unterricht eine große Bandbreite von unterschiedlichen Lösungsmöglichkeiten (Abb. 10; Abb. 11), welche aber trotzdem in die Reflexionsphase mit eingebracht werden konnten, da auch bei einer Erhöhung des Mittelsteins um drei oder 100 zu beobachten war, dass sich der Deckstein um das Doppelte erhöht. Diese Erkenntnisse wurden mit Hilfe der Entdeckungen der Kinder am Ende gemeinsam herausgearbeitet.
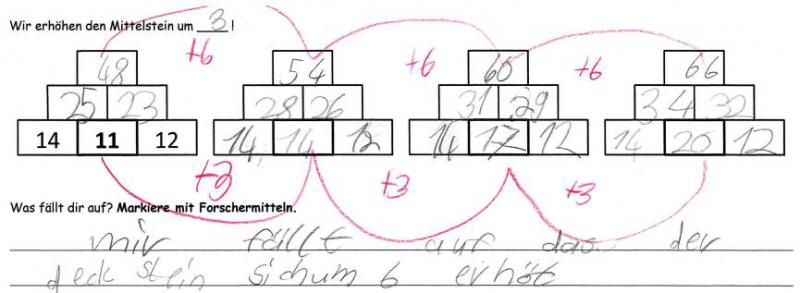 Abbildung 10
Abbildung 10
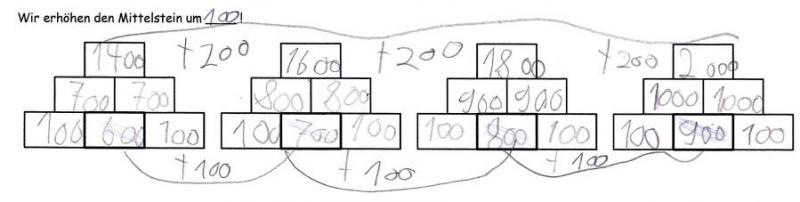 Abbildung 11
Abbildung 11
In der praktischen Anwendung fiel zudem auf, wie viel Potenzial adaptierbare Arbeitsaufträge im Zusammenhang mit offenen Aufgaben (vgl. ‚Offene Aufgaben‘) bieten. Die Freiheit, den Mittelstein um einen selbst gewählten Wert zu erhöhen, verleitete einen Großteil der Kinder dazu, die Ergebnisse mit der ursprünglichen Erhöhung um eins zu vergleichen, um dadurch neue Erkenntnisse zu gewinnen. So wurden auch die Beschreibungen ausführlicher. Interessant ist diesbezüglich ein Vergleich zweier Kinder, welche den Mittelstein um zwei erhöhten und einen Grund für die Erhöhung des Decksteins um vier suchten (Abb. 12; Abb. 13). Das unterschiedliche Niveau der Bearbeitung zeigt, dass die Aufträge auf verschiedenen Niveaustufen (vgl. ‚Anforderungsbereiche‘) bearbeitet werden können. Während ein Kind an einer konkreten Mauer versucht hat den Sachverhalt zu erklären (Abb. 13), war die Aussage eines anderen Kindes unter Hinzunahme von Fachwörtern schon wesentlich allgemeiner (Abb. 12).
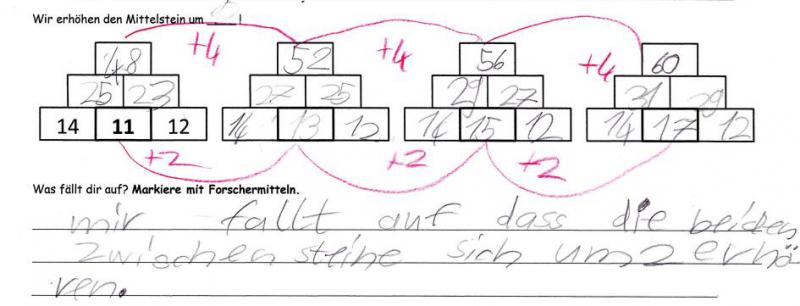 Abbildung 12
Abbildung 12
 Abbildung 13 (Bezug auf 2. Zahlenmauer von Abb. 12)
Abbildung 13 (Bezug auf 2. Zahlenmauer von Abb. 12)
Erweiterung durch Begründung und Beweis mit dem Darstellungsmittel „Plättchen“
Für leistungsstarke Kinder besteht die Möglichkeit nach der Überprüfung ihrer Vermutung diese auch zu begründen und zu beweisen. So werden sie zum Verallgemeinern angeregt, wodurch sie ihre Kompetenzen erweitern und zugleich mit ihren Erklärungen in der Reflexionsphase leistungsschwächeren Kindern dazu verhelfen können, das Kernanliegen zu erreichen. Die Schülerin in Abb. 14 hat bereits versucht, eine logische Implikation zu entwickeln.
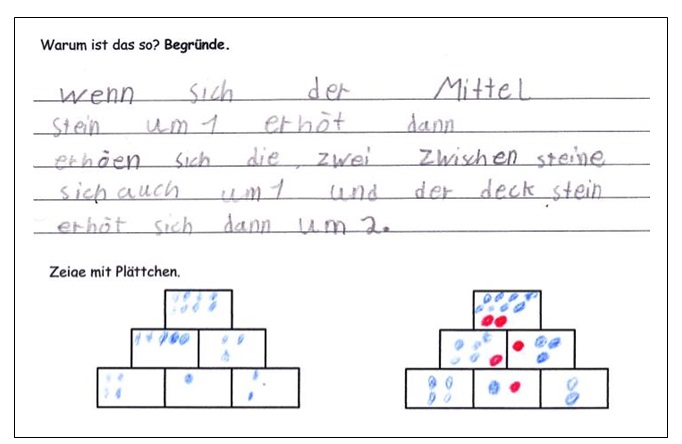 Abbildung 14
Abbildung 14
Auch anhand der offenen Aufgabenstellung (vgl. ‚Offene Aufgaben einsetzen‘), die Entdeckungen an eigenen Zahlenmauern zu überprüfen, ist ersichtlich, dass sich das Aufgabenformat gut für heterogene Lerngruppen eignet. Jeder Lernende überprüfte seine Vermutungen auf für ihn herausfordernde Weise (Abb. 15; Abb. 16).
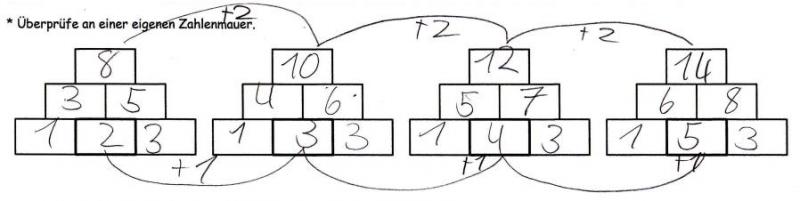 Abbildung 15
Abbildung 15
 Abbildung 16
Abbildung 16
Eine Gegenüberstellung der Schülerdokumente (Abb. 5-16) gibt einen Einblick in die große Spanne unterschiedlicher Leistungsniveaus innerhalb einer inklusiven Lerngruppe. Wohingegen Kinder mit Unterstützungsbedarf es schafften, mit Hilfe entsprechender Unterstützungsmaßnahmen, das Kernanliegen zu erreichen, wurden leistungsstärkere Kinder dazu angeregt Beweise zu entwickeln. Werden Aufgaben durch Bereitstellung von ‚Tipps und Herausforderungen‘ an unterschiedliche Voraussetzungen angepasst, kann die ganze Lerngruppe gemeinsam an einem Sachverhalt arbeiten und zugleich jedes Kind, unabhängig vom jeweiligen Leistungsstand, gefördert werden (vgl.
‚Planung von Förderung').
Weitere Anregungen
Um Auffälligkeiten zu entdecken und beschreiben zu können, benötigen manche Lernende mehr Rechenerfahrungen als andere. In diesem Fall besteht immer die Möglichkeit, weitere Arbeitsblätter mit anderen Zahlen aus den Vorlagen zu erstellen.
Eine Weiterführung der Unterrichtsreihe ist mit vertiefenden Einheiten verbunden, in denen beispielsweise das Vertauschen der Grundsteine (vgl.
Arbeitsblätter „Grundsteine vertauschen“) oder das Erstellen von Zahlenmauern mit besonders großen, kleinen oder bestimmten Decksteinen thematisiert werden. Diese Herangehensweise ermöglicht den Schülerinnen und Schülern eine Verinnerlichung des Lernstoffes, da ihr Wissen über die Auswirkungen operativer Veränderungen nun auf unterschiedliche Weise Anwendung findet. Die Arbeitsblätter sowie Arbeitsaufträge werden dazu – wie oben beschrieben – dementsprechend angepasst.
Generell ist das Einsetzen von „Tippkarten“ bei zahlreichen Unterrichtseinheiten sinnvoll. Richtig angewendet können sie eine tragende Rolle im Unterstützungsprozess übernehmen. Bei der Formulierung von „Tipps“ (auch verbal) ist jedoch darauf zu achten, dass sie in der praktischen Anwendung dem Kind lediglich als unterstützende Hilfe auf dem Weg zum Kernanliegen dienen sollen. „Tippkarten“ sollten keineswegs als Lösungskarten fungieren, die den Kindern den Denkprozess vorwegnehmen.
Je nach Intention können „Tipps“ unterschiedlich formuliert werden (vgl.
„Anregungen zur Formulierung von Tipps und Herausforderungen"), z.B. um …
Die „Tippkarten“ sollten klar und verständlich formuliert sein, damit die Kinder nicht schon am Verstehen der „Tipps“ scheitern. Unabdingbar ist dabei die Verwendung von Abbildungen, die die Erklärungen sinnvoll unterstützen (vgl. Tippkarten „Zahlenmauern“).
Analog zu „Tippkarten“ können auch weiterführende Herausforderungen erstellt werden, welche leistungsstärkere Kinder zum Übertragen ihrer Erkenntnisse auf weitere Beispiele auffordern und/oder zum Begründen und Verallgemeinern (vgl. ‚Anforderungsbereiche‘) anregen.
Mögliche Formulierungen sind beispielsweise „Überprüfe an einer eigenen Zahlenmauer, an einem eigenen Entdeckerpäckchen, …“ oder aber „Warum ist das so? Begründe.“ Eine sinnvolle Herangehensweise, durch die beide Seiten profitieren können, wäre Tippkarten für andere Kinder erstellen zu lassen („Wie kannst du anderen Kindern erklären, warum … Schreibe deinen Tipp auf.“). Auch das Entwickeln von Strategien kann eine „Herausforderung“ darstellen („Beschreibe einen Trick, wie wir schlau …“) und zum Verallgemeinern anregen.