Wie in allen Sprachen im asiatischen Raum, die sich aus dem Altchinesischen ableiten, werden im Koreanischen Zahlwörter sehr systematisch und mit Bezug zur Notation von Zahlen gebildet: „Zuerst wird der Nennwert einer Bündelungseinheit (also die Anzahl der Bündel), dann der dazugehörige Stellenwert (also die Größe der dazugehörigen Bündelungseinheit) genannt, dann die Anzahl der nächst kleineren Bündel, dann die dazugehörige Bündelungseinheit usw“ (Schulz 2014, S. 147). Im Unterschied zur Notation, bei der ja der Stellenwert durch die Position in einer Ziffernfolge bestimmt wird, werden bei der Bildung der Zahlwörter die Bündelungseinheiten mitgenannt.
|
Zahlwortbildung in Korea (ins Deutsche übersetzt)
|
|
Bildungsregel
|
Anzahl der Hunderter
|
hundert
|
Anzahl der Zehner
|
zehn
|
Anzahl der Einer
|
|
11
|
|
|
|
zehn
|
eins
|
|
21
|
|
|
zwei
|
zehn
|
eins
|
|
56
|
|
|
fünf
|
zehn
|
sechs
|
|
356
|
drei
|
hundert
|
fünf
|
zehn
|
sechs
|
Bezogen auf zweistellige Zahlwörter zeichnet sich das deutsche Zahlwortsystem beispielsweise aus durch Inkonsistenzen zwischen dem gesprochenen Zahlwort und der Abfolge der Ziffern in der geschriebenen Zahl.
Diese Inkonsistenzen erfordern einen Inversionsprozess während des Lesens und Schreibens von Zahlen: Entgegen der eigentlichen Lese- bzw. Schreibrichtung (von links nach rechts) lautet eine Bildungsregel für zweistellige Zahlwörter im deutschen Sprachraum:
"[Anzahl Einer]-und-[Anzahl Zehner]-zig" (Wartha & Schulz 2012, S. 52).
Ein weiterer elementarer Unterschied zwischen Zahlwort und notierter Zahl besteht darin, dass das Zahlwortsystem zur Bildung der Zahlwörter allein mit dem Bündelungssystem auskommt. So wird beispielsweise bei der Bildung der Zahlwörter bis 99 die Zehnerbündelung durch das Anhängen der Endsilbe „-zig“ angezeigt und benannt (vgl. Schulz 2014).
|
[Anzahl der Einer] – und – [Anzahl der Zehner] – zig
|
|
56
|
sechs - und - fünf - zig
|
"Im gesprochenen Zahlwort – also in der Wortform – benutzen wir also kein Stellenwertsystem, sondern nur ein reines Bündelungssystem. Erst auf der Ebene der Ziffer des geschriebenen Zahlwortes spielt der Stellenwert eine zentrale Rolle, arbeiten wir also mit dem Stellenwertsystem“ (Padberg, 2007, S.11f).
Diese Sprechweise stützt das Verständnis der Zehner-Einer-Struktur von zweistelligen Zahlen allerdings nur bedingt. So kann z.B. aus dem Zahlwort sechsundfünfzig (fünf-zig) nicht direkt geschlossen werden, dass es sich um fünf Zehner (und sechs Einer) handelt.
Darüber hinaus gibt es von dieser "Bildungsregel" etliche Ausnahmen, die es zusätzlich erschweren, die Zehner-Einer-Struktur zu erkennen und zu nutzen:
-
So gibt es beispielsweise für die ersten beiden zweistelligen Zahlen 11 und 12 ein eigenes Zahlwort.
-
Bei den Zahlen 13 bis 19 lautet die Endsilbe „zehn“ (nicht „zig“) und es fehlt das verbindende "und“.
-
Statt von „zwei-zig“ wird von „zwan-zig“ gesprochen (auch bei den Zahlen 21 bis 29).
-
Die Endsilbe „-zig“ wird bei den Zahlen 30 bis 39 phonetisch verändert in „-ßig“.
-
...
Neben den konventionell gebildeten Zahlwörtern gibt es weitere verbal-symbolische Zahldarstellungen:
 Abbildung 2: Verbal-symbolische Zahldarstellungen (Beispiele)
Abbildung 2: Verbal-symbolische Zahldarstellungen (Beispiele)
Schriftlich-symbolische Zahldarstellungen
Unter Zahlzeichen wird die Verschriftlichung einer Zahl verstanden. Am häufigsten Verwendung findet die sogenannte Normalform (z.B. "361").
Neben dieser Darstellungsform einer Zahl / der Normalform lassen sich weitere Schreibweisen unterscheiden wie z.B.: "3H 6Z 1E" (Schreibweise mit Zehnern und Einern) oder 300 + 60 + 1 (Summenschreibweise).
 Abbildung 3: Schriftlich-symbolische Zahldarstellungen (Beispiele)
Abbildung 3: Schriftlich-symbolische Zahldarstellungen (Beispiele)
Von Bedeutung für die Entwicklung eines tragfähigen Stellenwertverständnisses sind zudem unkonventionelle Schreibweisen bzw. Zahlzeichen wie beispielsweise 3H 5Z 11E (für die Zahl 361) oder auch Veränderungen in der Anordnung der Stellen (vgl. hierzu die Abschnitte Feststellung der Lernausgangslage und Didaktische Folgerungen).
Hierdurch können Kinder verstärkt herausgefordert werden, Zahlen zu deuten und sich mit dem dezimalen Stellenwertsystem auseinanderzusetzen (vgl. Mosandl & Nührenbörger, 2014).
In einem engen Zusammenhang mit dem Zahlzeichen stehen das Bündelungs- und das Stellenwertprinzip, d.h. die Anwendung des Stellenwert- und Bündelungsprinzips ist für die Verschriftlichung eines Bündelungsvorganges als Zahlzeichen notwendig.
Hat man im dekadischen System eine gegebene Anzahl von Elementen fortgesetzt gebündelt, werden die Bündelungsergebnisse (als schriftlich-symbolische Zahldarstellungen) unter Anwendung des Stellenwertsystems notiert. "Zur Erstellung eines Zahlzeichens ist es zunächst notwendig den Zahlenwert der Ziffer bestimmen zu können. Diese Zuordnung wird für 0 bis 9 gelernt. Bei der Bildung eines zweistelligen Zahlzeichens finden Stellenwert- und Bündelungsprinzip Beachtung" (Fromme, 2017, S. 44).
Anschauliche Zahldarstellungen
Unter der Repräsentationsform "anschauliche Zahldarstellungen" wird im Folgenden die Darstellung von Zahlen mittels Materialien und durch Veranschaulichungen gefasst.
 Abbildung 4: Anschauliche Zahldarstellungen (Beispiele)
Abbildung 4: Anschauliche Zahldarstellungen (Beispiele)
Im Hinblick auf "große" Zahlen liegt der Schwerpunkt hier auf Materialien und Veranschaulichungen, die eher didaktisch geprägt sind, wie z.B. Wendeplättchen, Rechenrahmen, Mehrsystemblöcke oder ikonische Darstellungen wie z.B. Zahlenstrahl und Punktefeld etc..
Ein weiterer wichtiger Aspekt ist, dass eine Menge von Elementen durch verschiedene Darstellungen und Bündelungszustände repräsentiert werden kann. Werden diese verschiedenen Darstellungen in Beziehung zueinander gesetzt, bieten sie Raum für Deutungen und Interpretationen (vgl. Fromme, 2017, van de Walle, 1994):
 Abbildung 5
Abbildung 5
Übersetzungen
Gelingt es Kindern (oder Erwachsenen), den Repräsentanten einer Repräsentationsform in einen anderen Repräsentanten umzuwandeln, dann sprechen wir von einer "Übersetzung".
Damit sind aber nicht nur Übersetzungen zwischen den verschiedenen Zahlrepräsentationen bzw. Repräsentationsformen gemeint (wie z.B. die Umwandlung eines Zahlzeichens in ein Zahlwort), vielmehr können Übersetzungen auch innerhalb einer Zahlrepräsentation – d.h. beispielsweise von einer Zahldarstellung in eine andere – stattfinden.
Die Fähigkeit, zwischen und innerhalb verschiedener Zahlrepräsentationen flexibel zu übersetzen und die Zusammenhänge begründen zu können, stellt einerseits einen Indikator für ein tragfähiges Stellenwertverständnis dar (vgl. Fuson et al., 1997). Andererseits wird die Entwicklung des Stellenwertverständnisses durch die Anforderung, Zahldarstellungen in Zahlzeichen, Zahlworte in Zahldarstellungen, Zahlzeichen in Zahlworte etc. zu übersetzen, zugleich gefördert (vgl. Schulz & Schülke, 2017; Kuhnke, 2013).
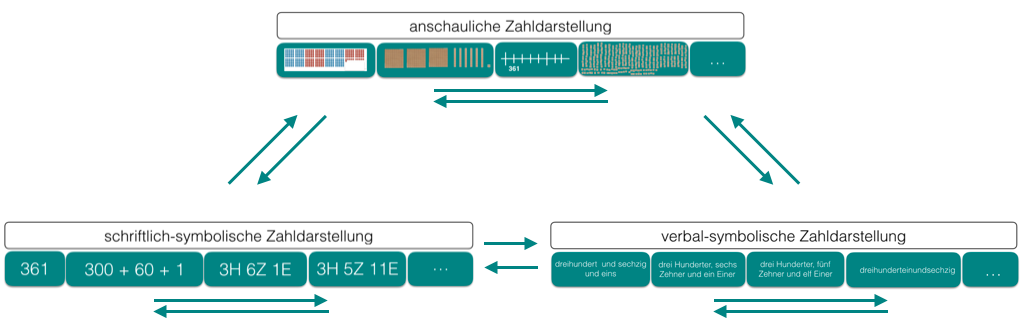 Abbildung 6
Abbildung 6
Voraussetzungen
Wie bereits dargestellt und erläutert wurde, stellen das Prinzip der fortgesetzten Bündelung und das Stellenwertprinzip eine Grundvoraussetzung für flexible Übersetzungsprozesse zwischen den verschiedenen Zahlrepräsentationen dar.
Doch während sich die beiden Prinzipien auf einer rein fachlichen Ebene gut beschreiben lassen, bleibt zunächst offen, über welche Lernvoraussetzungen Kinder verfügen müssen, um Einsicht in diese beiden grundlegenden Prinzipien des Stellenwertsystems erlangen zu können.
Bündelungsprinzip
Über das Konzept des Bündelns (hier geht es zunächst um das einfache Zusammenfassen von einzelnen Elementen zu einem „Bündel“) kann das Verständnis der fortgesetzten Bündelung entwickelt werden: Die Idee des fortgesetzten Bündelns beinhaltet die Bündelung von bestehenden "Bündeln", d.h. von bereits gebündelten Elementen (vgl. Schulz, 2014, S. 151; Fromme, 2017).
Hierbei kommt dem Zählen, d.h. zum einen dem Zählen in Einerschritten, aber auch dem Zählen von Gruppen und von einzelnen Elementen eine besondere Bedeutung zu (vgl. van de Walle, 2007)
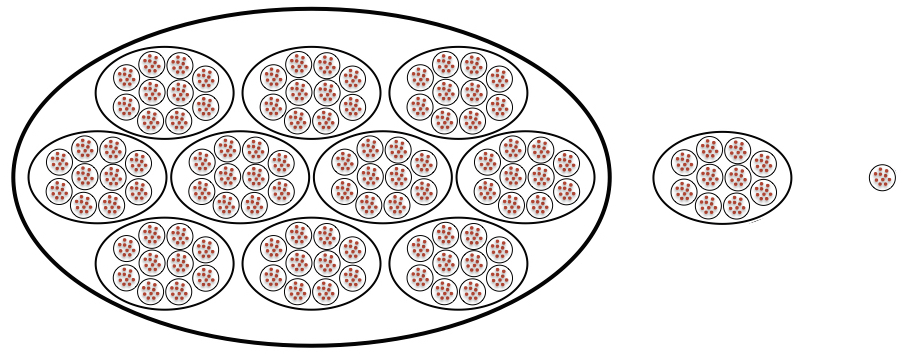 Abb. 7: Fortgesetzte Bündelung
Abb. 7: Fortgesetzte Bündelung
"Notwendig hierfür ist ein tragfähiges Teil-Ganzes-Verständnis – also das grundsätzliche Verständnis dafür, dass Zahlen aus anderen Zahlen zusammengesetzt sind, und dass sie unverändert bleiben, auch wenn sie gebündelt sind“ (Schulz, 2014, S. 151)
Eine ausführliche Darstellung des Teil-Ganzes-Verständnisses und der Bedeutung dieses Konzepts für den Aufbau von tragfähigen Zahlvorstellungen im Zahlenraum bis 100 finden Sie in unter Zahlvorstellungen: Hintergrund.
Kinder müssen darüber hinaus wissen, dass in diesen Bündeln immer die gleiche Anzahl von Elementen enthalten ist (d.h. mit Blick auf das Dezimalsystem immer zehn – und nicht mal neun oder mal acht Elemente etc.), und dass zudem in allen Bündeln immer gleich viele Elemente enthalten sind (vgl. Schulz, 2014).
Stellenwertprinzip / Notation der Zahlen
Gilt es, eine Zahldarstellung in ein Zahlzeichen zu übersetzen, d.h. eine Zahl (in Normalform) zu notieren, dann müssen die Kinder mehrere Aspekte beachten:
Beim Schreiben von Zahlen werden die Bündelungseinheiten nicht erfasst – vielmehr wird die Bündelungseinheit durch die Position der entsprechenden Ziffer im Zahlzeichen festgelegt. Die Anzahl der Bündel wird dann durch die Ziffer angegeben.
Deutlich wird an dieser Stelle, wie eng die Schreibweise der Zahlen mit dem Bündelungsprinzip verbunden ist. Ein Verständnis des Stellenwertprinzips basiert auf "Einsicht in das Konzept der Bündelung zusammen mit der Kenntnis der Konventionen der Notation" (Schulz, 2014, S. 151, Hervorhebung im Original).
Erwerb eines tragfähigen Stellenwertverständnisses
Mögliche Hürden und didaktische Folgerungen
In verschiedenen Studien konnte gezeigt werden, dass auch in höheren Klassen nicht alle Schülerinnen und Schüler über ein umfassendes und tragfähiges Stellenwertverständnis verfügen (vgl. Moser Opitz, 2013).
Hinzu kommt, dass insbesondere Schülerinnen und Schüler mit Lernschwierigkeiten Fehlvorstellungen und Defizite in Bezug auf das dezimale Stellenwertsystem aufweisen und keinen Zugriff auf die wesentlichen Prinzipien des dezimalen Stellenwertsystems haben, obwohl diese zum Teil bereits im zweiten Schuljahr im Mathematikunterricht der Grundschule thematisiert werden. (vgl. Kamii, 1986; Moser Opitz, 2007; Scherer, 2011).
Vor diesem Hintergrund stellt sich zum einen die Frage, welche spezifischen Schwierigkeiten oder Hürden die Entwicklung eines tragfähigen Stellenwertverständnisses behindern bzw. verhindern können. Zum anderen, warum oft erst spät erkannt wird, wenn Kinder Schwierigkeiten mit dem dezimalen Stellenwertsystem haben.
Zum anderen geht es um die didaktischen Folgerungen, die aus den bisherigen Überlegungen zum dezimalen Stellenwertsystem für den Mathematikunterricht in der Grundschule abgeleitet werden können:
Wie kann es im Unterricht gelingen, alle Kinder – unabhängig von ihren jeweiligen Lernvoraussetzungen und individuellen Schwierigkeiten – bei der Entwicklung eines tragfähigen Stellenwertverständnisses zu unterstützen?
Bündelungsprinzip: Zeigen Kinder Verständnisschwierigkeiten in Bezug auf das Prinzip der fortgesetzten Bündelung, kann das unterschiedliche Gründe haben:
-
Das Verständnis des Teil-Ganzes-Konzeptes ist nicht gesichert:
Für das Verständnis der Bündelung und der Stellenwerte ist es wichtig, dass die Kinder Zahlen nicht nur ordinal (z.B. als Elemente in einer Abfolge von Zahlen) verstehen, sondern erkennen, dass Zahlen zerlegbar und aus anderen Zahlen zusammengesetzt sind (so kann z.B. die Zahl 61 in 60 und 1 zerlegt werden, die Zahl 60 besteht aus sechs Zehnerbündeln etc.).
-
Den Lernprozess bzw. die Einsicht in die Zerlegbarkeit von Zahlen zusätzlich erschweren kann die Vorstellung einiger Kinder, dass auch über den Zahlraum bis 12 hinaus zu jeder Zahl ein eigenes Zahlwort bzw. zu jeder Zahl über 9 ein neues Zahlzeichen gelernt werden muss. Wichtig ist in diesem Zusammenhang die Erkenntnis, dass sowohl die Schreibweise von Zahlen (Zahlzeichen) als auch die Bildung der Zahlwörter bestimmten Regeln folgt.
Diese Erkenntnis kann allerdings dadurch erschwert werden, dass beispielsweise die Zahlwortbildung im deutschen Sprachraum viele Unregelmäßigkeiten und Ausnahmeregelungen aufweist.
-
Erstrecken sich die Bündelungsaktivitäten im Unterricht nur auf den Zahlenraum bis 100, wird die Einsicht in grundlegende Prinzipien verhindert und das Bündelungsprinzip (sowie das Stellenwertprinzip) kann nicht voll erfasst werden: "Die Grundidee der dezimalen Struktur wird erst im Zahlenraum bis 1000 richtig sichtbar. Erst wenn zehn Hunderter zu einem Tausender gebündelt werden, findet eine Bündelung dritter Ordnung statt, und das Prinzip der fortgesetzten Bündelung wird deutlich“ (Scherer & Moser Opitz, 2010, S. 140; Mosandl & Nührenbörger, 2014).
Zahlwortbildung: Wie bereits dargestellt, unterscheidet sich die Zahlwortbildung in den einzelnen Ländern und Sprachräumen erheblich. So findet man neben Ländern, in denen die Zahlwortbildung regelgeleitet und ohne Unregelmäßigkeiten erfolgt (wie z.B. in Korea und Japan) andere Länder, in denen es zwar auch Regeln für die Bildung von Zahlwörtern gibt, diese jedoch durch viele Ausnahmen unterbrochen werden (wie z.B. in Frankreich, Großbritannien oder auch in Deutschland).
Durch vergleichende Studien konnte gezeigt werden, dass „die Regelmäßigkeit oder Unregelmäßigkeit der Zahlwortbildung in einer Sprache Auswirkungen haben auf die Entwicklung des Stellenwertverständnisses“ (Schulz, 2014, S. 168).
Übersetzungsprozesse: In Vorbereitung (Hürden und didaktische Folgerungen)