Seite "Austausch anregen" in einfacher Sprache
Der inklusive Mathematikunterricht sollte Schülerinnen und Schüler jeden Leistungsniveaus individuell fördern. Dabei ist besonders darauf zu achten, dass es zu keiner Vereinzelung der Lernenden kommt, sondern dass das Lernen mit- und voneinander angeregt wird. Demzufolge ist in einem inklusiven Unterricht auf „eine ausgewogene Balance zwischen differenzierenden und integrierenden Lernsituationen“ (Wocken, 1998, S. 50) zu achten.
Integrierende Lernsituationen, in denen mit- und voneinander gelernt wird, setzen einen gemeinsamen Austausch über Mathematik voraus, in welchem über Entdeckungen, Lösungsprodukte, -ideen und -wege mit dem Ziel des wechselseitigen Verstehens verbal und non-verbal interagiert wird (s. Abb.1 Mitte). Eine besondere Herausforderung bildet dabei die Tatsache, dass ein Austausch immer aus zwei Aspekten besteht: andere verstehen (Sprachverstehen; s. Abb.1 Mitte rechts) und verstanden werden (Sprachverwendung; s. Abb.1 Mitte links). Beide Aspekte müssen daher gezielt unterstützt werden. Wesentlich dafür ist, allen Lernenden die Möglichkeit zu geben, individuelle Zugänge und Lösungsprozesse sowie „eigene Ideen zu entwickeln und über diese in den Austausch zu treten, um somit gemeinsame, an der Mathematik orientierte, Gespräche zu initiieren, die nicht alleine durch die Perspektive der Lehrkraft geprägt sind“ (Brandt & Nührenbörger, 2009, S. 29; s. auch Abb.1 oben). Es geht folglich sowohl um Gespräche, in die die Lehrkraft involviert ist, als auch um den Austausch zwischen den Schülerinnen und Schülern untereinander.
In der Auseinandersetzung mit den Gedanken anderer steckt die Chance, die Vielfalt im inklusiven Mathematikunterricht als Potential und Lernanlass zu nutzen, denn sie kann zum Nachdenken und zu einer Fragehaltung anregen. Hierdurch werden die Weiterentwicklung eigener Entdeckungen, Lösungsprodukte, -ideen und -wege vor dem Hintergrund individueller Zugänge ermöglicht (Abb.1 unten). Dem gemeinsamen Austausch im inklusiven Unterricht kommt folglich die wichtige Rolle als, „Motor" inhaltsbezogener Lernprozesse zu, indem Stärken und Schwächen zur Normalität gehören und als Chance für das mit- und voneinander Lernen betrachtet werden. Darüber hinaus werden ebenso prozessbezogene Kompetenzen durch den Austausch über Mathematik gefördert.
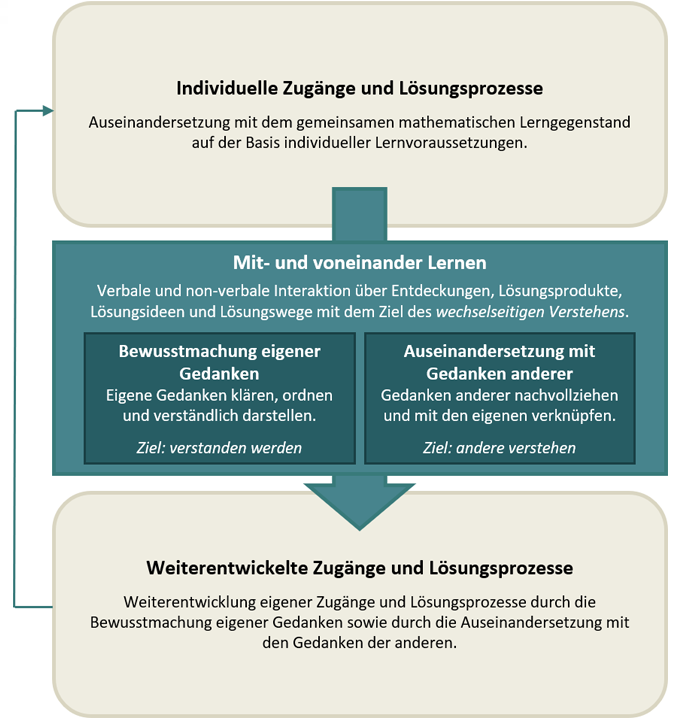 Abbildung 1: Mit- und voneinander Lernen durch den gemeinsamen Austausch
Abbildung 1: Mit- und voneinander Lernen durch den gemeinsamen Austausch
(Korten, 2020, S. 120)
Für die erfolgreiche Anregung eines mathematischen Austausches im inklusiven Unterricht sind folgende übergreifende Prinzipien zu beachten:
-
Gegenstandsreichhaltigkeit als Voraussetzung (Korten, 2020)
Reichhaltigkeit meint, dass ein geeigneter Lerngegenstand einerseits zieldifferente Lernanlässe ermöglicht und ebenso vielfältige sinnvolle Austauschgelegenheiten über einen gemeinsamen mathematischen Kern für heterogene Lernende bietet. Dahingehend ist eine umfassende Analyse des mathematischen Lerngegenstandes die Voraussetzung, um mathematische Gespräche zwischen Schülerinnen und Schüler mit stark heterogenen Lernvoraussetzungen und individuellen Leistungsständen über einen gemeinsamen Gegenstand zu ermöglichen.
-
„Eine vorgeschaltete individuelle Phase, um ein Sich-Einbringen-Können sowie Anerkennung und Wertschätzung aller zu unterstützen“ (ebd., S. 365).
Eine potentiell austausch- und zugleich lernförderliche Bedingung stellt eine individuelle Phase vor der gemeinsamen Phase des Austausches dar. Hierdurch wird allen Schülerinnen und Schülern zunächst einen individuellen Zugang zu dem gemeinsamen mathematischen Gegenstand gewährleistet, um ihnen anschließend die Chance zu ermöglichen, sich am Austausch beteiligen zu können (Abb. 1 oben). Die methodische Organisationsform des gemeinsamen Austausches (z.B. Ich-Du-Wir Methode, Mathekonferenz) ist je nach beabsichtigtem Austauschprozess variabel zu gestalten. Wichtig ist jedoch in jedem Fall, dass die Schülerinnen und Schüler zunächst die Gelegenheit erhalten, sich individuell mit dem gemeinsamen Gegenstand bzw. der gemeinsamen Aufgabe vertraut zu machen.
-
Anregung des Darstellungswechsels als Chance (ebd.)
Die Ermöglichung und gezielte Herausforderung der Nutzung unterschiedlicher Darstellungsformen (enaktiv, ikonisch, symbolisch, sprachlich-symbolisch; s. auch ‚Darstellungsformen‘) ermöglicht diese individuellen heterogenen Zugänge zum gemeinsamen mathematischen Gegenstand. Des Weiteren erleichtert die Herausforderung des Darstellungswechsels die anschließende Kommunikation, indem die verschiedenen Darstellungsebenen dazu beitragen, die heterogenen Zugänge zu verknüpfen.
Zentral für die Anregung mathematischer Gespräche ist weiterhin ein Unterricht, der
-
austauschanregende Aufgaben bereit hält,
-
den Austausch methodisch strukturiert und unterstützt, um eine kognitive und soziale Entlastung bei den Lernenden zu gewährleisten sowie
-
eine differenzsensible pädagogische Haltung der Lernbegleitung, die individuelle Lernprozesse zielbewusst anregt und heterogene Lernprozesse begleitet (Selter & Spiegel, 2003, S. 54)
Sich verständlich machen
Ein wesentlicher Aspekt mathematischen Austausches ist die Bewusstmachung eigener Gedanken (Abb. 1 Mitte links). Dazu gehört es, diese zu klären und zu ordnen sowie für andere verständlich und zunehmend mathematisch darzustellen. Dies kann einerseits durch verbale Äußerungen und Erklärungen erfolgen, aber auch Handlungen am Material sowie Mimik und Gestik tragen zum Austausch bei.
Andere verstehen
Der zweite bedeutende Aspekt mathematischen Austausches ist das Auseinandersetzen mit den Gedanken anderer (Abb. 1 Mitte rechts). Dazu gehört es, die Gedanken und Äußerungen der anderen nachzuvollziehen und mit den eigenen zu verknüpfen. So findet auf Grundlage der eigenen individuellen Zugänge das Nachdenken über die Zugänge der Kommunikationspartner statt, wodurch eine Weiterentwicklung angeregt werden kann.
Gespräche im Klassenverband
Nicht nur Partner- und Gruppenarbeit bieten Anlass für einen mathematischen Austausch. Ebenso ergeben sich in einem heterogenen Klassenverband viele Gelegenheiten, mathematische Gespräche gezielt anzuregen und einen zunehmend fachsprachlichen Austausch zu unterstützen. Hierzu gehören beispielsweise Einstiegs-, Sammlungs- und Reflexionsphasen.
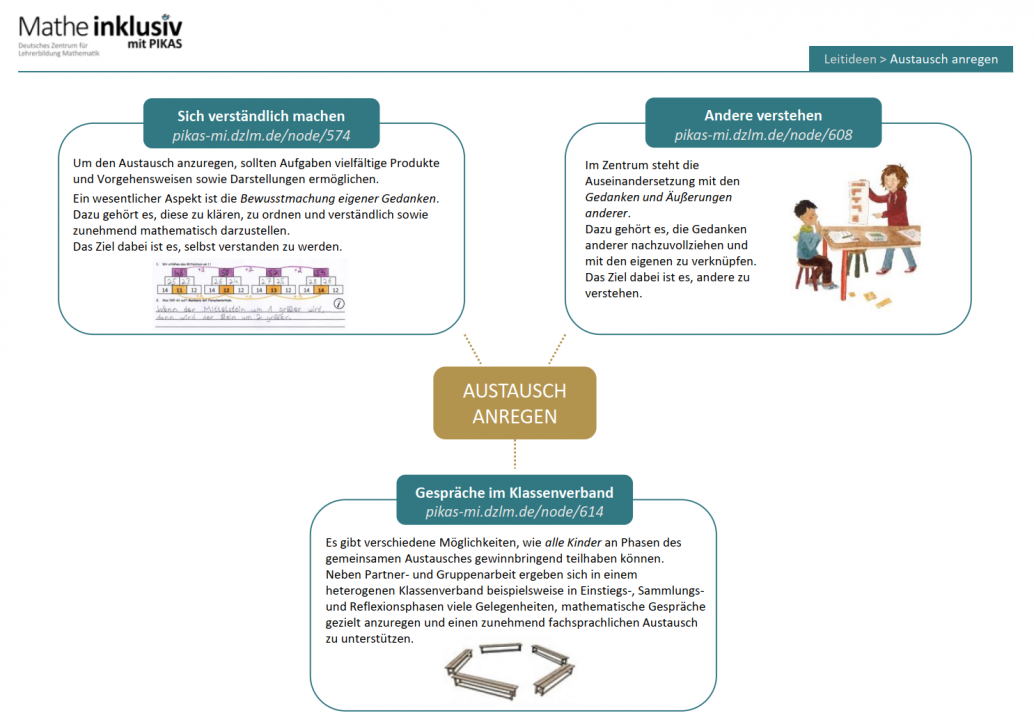 Plakat 'Austausch anregen'
Plakat 'Austausch anregen'