Erweiterung ("Zahlen zerlegen")
Tipp: Die Materialien zu den Aufgabenstellungen finden Sie hier (in Vorbereitung).
Zerlegen selbst gewählter 'großer' Zahlen.
Material: AB mit leeren Zahlenhäusern
Die Kinder wählen selber Zahlen aus, zu denen sie Zerlegungen finden und in Zahlenhäuser notieren. Je nach ausgewählten Zahlen können die erstellten Zahlenhäuser im Anschluss
verglichen und mögliche Analogien entdeckt werden (z.B. Zahlenhäuser zur 6 und 16).
Material: AB mit leeren Zahlenhäusern
Die Kinder wählen selber Zahlen aus, zu denen sie Zerlegungen finden und in Zahlenhäuser notieren. Je nach ausgewählten Zahlen können die erstellten Zahlenhäuser im Anschluss
verglichen und mögliche Analogien entdeckt werden (z.B. Zahlenhäuser zur 6 und 16).
Vergleichen von Zahlenhäusern.
Material: AB mit leeren Zahlenhäusern
Die Kinder notieren die Zahlzerlegungen zu mehreren Zahlen (Nachbarzahlen) systematisch in Zahlenhäusern, vergleichen anschließend die Zahlenhäuser miteinander und notieren bzw. markieren, was ihnen auffällt.
„Vergleiche die Zahlenhäuser. Was fällt dir auf?“
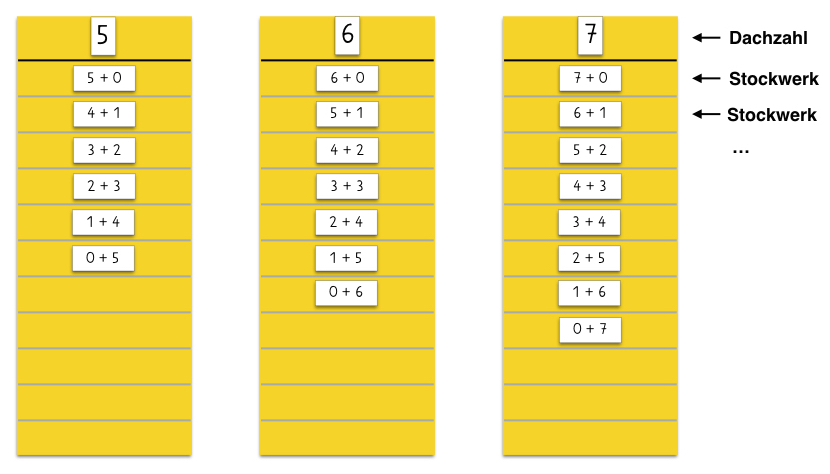
Abbildung 1
Mögliche Entdeckungen:
- Je größer die Dachzahl, desto mehr Stockwerke sind nötig.
- Bei Häusern mit aufeinander folgenden Dachzahlen (z.B. 5,6,7,8,..) wächst die Anzahl der benötigten Stockwerke jeweils um 1.
- Die Dachzahl + 1 ergibt jeweils die Anzahl der benötigten Stockwerke.
- Verdoppelungsaufgaben kommen nur bei geraden Dachzahlen vor.
- Wenn die Anordnung der Zahlzerlegungen dem obigen Beispiel entspricht: Der zweite Summand ist in den jeweiligen Stockwerken immer gleich.
- …
Material: AB mit leeren Zahlenhäusern
Die Kinder notieren die Zahlzerlegungen zu mehreren Zahlen (Nachbarzahlen) systematisch in Zahlenhäusern, vergleichen anschließend die Zahlenhäuser miteinander und notieren bzw. markieren, was ihnen auffällt.
„Vergleiche die Zahlenhäuser. Was fällt dir auf?“

Abbildung 1
Mögliche Entdeckungen:
- Je größer die Dachzahl, desto mehr Stockwerke sind nötig.
- Bei Häusern mit aufeinander folgenden Dachzahlen (z.B. 5,6,7,8,..) wächst die Anzahl der benötigten Stockwerke jeweils um 1.
- Die Dachzahl + 1 ergibt jeweils die Anzahl der benötigten Stockwerke.
- Verdoppelungsaufgaben kommen nur bei geraden Dachzahlen vor.
- Wenn die Anordnung der Zahlzerlegungen dem obigen Beispiel entspricht: Der zweite Summand ist in den jeweiligen Stockwerken immer gleich.
- …
Zerlegen von Zahlen in drei Teile.
Material: AB
Die Kinder werden angeregt, eine Zahl (z.B. 6) in drei (oder mehr) Teile zu zerlegen und verschiedene Möglichkeiten zu finden.
Um die Anzahl der möglichen Zerlegungen zu begrenzen, kann es sinnvoll sein, die leere Menge als mögliche Teilmenge auszuschließen und nur Mengen mit mindestens einem Element zuzulassen - zumal es darüber hinaus schwierig ist, Zerlegungen mit leeren Teilmengen an einer Punktereihe mit Stiften darzustellen bzw. durch Zerschneiden herzustellen.
Wird die leere Menge als mögliche Teilmenge zugelassen, ist es angezeigt, die Zerlegung nur auf der symbolischen Ebene durchzuführen. Hier wird die Zerlegung beispielsweise mittels Zahlentripeln oder als Additionsaufgabe dargestellt, die die Anzahl der Elemente in einer Teilmenge bezeichnen. D.h. das Zahlentripel 0 / 0 / 6 entspricht einer Zerlegung in zwei leere Teilmengen und in eine Teilmenge mit 6 Elementen.
Finde alle (verschiedene) Möglichkeiten. Wie gehst du vor?“
Beispiel mit Angabe der möglichen Zahlzerlegungen.
Zerlegung der Zahl 6 in drei Teile / die leere Menge ist als Teilmenge zugelassen:

Abbildung 2
Beispiel mit Angabe der möglichen Zahlzerlegungen.
Zerlegung der Zahl 6 in drei Teile / die leere Menge ist als Teilmenge nicht zugelassen:

Abbildung 3
Material: AB
Die Kinder werden angeregt, eine Zahl (z.B. 6) in drei (oder mehr) Teile zu zerlegen und verschiedene Möglichkeiten zu finden.
Um die Anzahl der möglichen Zerlegungen zu begrenzen, kann es sinnvoll sein, die leere Menge als mögliche Teilmenge auszuschließen und nur Mengen mit mindestens einem Element zuzulassen - zumal es darüber hinaus schwierig ist, Zerlegungen mit leeren Teilmengen an einer Punktereihe mit Stiften darzustellen bzw. durch Zerschneiden herzustellen.
Wird die leere Menge als mögliche Teilmenge zugelassen, ist es angezeigt, die Zerlegung nur auf der symbolischen Ebene durchzuführen. Hier wird die Zerlegung beispielsweise mittels Zahlentripeln oder als Additionsaufgabe dargestellt, die die Anzahl der Elemente in einer Teilmenge bezeichnen. D.h. das Zahlentripel 0 / 0 / 6 entspricht einer Zerlegung in zwei leere Teilmengen und in eine Teilmenge mit 6 Elementen.
Finde alle (verschiedene) Möglichkeiten. Wie gehst du vor?“
Beispiel mit Angabe der möglichen Zahlzerlegungen.
Zerlegung der Zahl 6 in drei Teile / die leere Menge ist als Teilmenge zugelassen:

Abbildung 2
Beispiel mit Angabe der möglichen Zahlzerlegungen.
Zerlegung der Zahl 6 in drei Teile / die leere Menge ist als Teilmenge nicht zugelassen:

Abbildung 3
Ergänzen von Zahlzerlegungen.
Material: Sortiertafel, Papierstreifen mit abgebildeten Punkten, Ergänzungsstreifen, Streifen mit Additionsaufgaben (ein Summand verdeckt)
Die Kinder haben die Aufgabe, unvollständig vorgegebene Zahlzerlegungen zu ergänzen.
Vorgegeben werden Additionsaufgaben, bei denen ein Summand verdeckt ist.

Abbildung 4
Bei Bedarf können die Ergänzungen im Anschluss überprüft werden:
Auf bzw. unter eine Darstellung der Gesamtmenge werden die Teilmengen gelegt und die Passung der ergänzten Teilmengen wird kontrolliert.
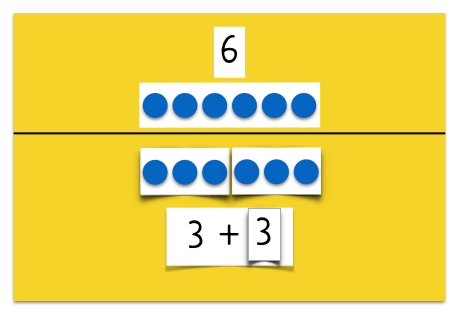
Abbildung 5
Material: Sortiertafel, Papierstreifen mit abgebildeten Punkten, Ergänzungsstreifen, Streifen mit Additionsaufgaben (ein Summand verdeckt)
Die Kinder haben die Aufgabe, unvollständig vorgegebene Zahlzerlegungen zu ergänzen.
Vorgegeben werden Additionsaufgaben, bei denen ein Summand verdeckt ist.

Abbildung 4
Bei Bedarf können die Ergänzungen im Anschluss überprüft werden:
Auf bzw. unter eine Darstellung der Gesamtmenge werden die Teilmengen gelegt und die Passung der ergänzten Teilmengen wird kontrolliert.

Abbildung 5


