Erweiterung ("Lege nach und schreibe auf")

Vorgabe von unkonventionellen Zahldarstellungen

Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB

Analog zur Aufgabenstellung „Lege nach und schreibe auf“ (Basisaufgabe) legen die Kinder bei dieser Aufgabenstellung der Erweiterung Zahlenbilder mit Legematerial nach und notieren die Zahldarstellung. 

Im Gegensatz zur Basisaufgabe stehen im Vordergrund der Erweiterung allerdings „unkonventionelle“ Zahldarstellungen mit beispielsweise 2 Hunderterplatten, 12 Zehnerstangen und 4 Einerwürfeln.

Die Kinder legen das vorgegebene Zahlenbild nach, werden angeregt, weiter zu bündeln („Immer zehn bündeln“) und ordnen das Material nach Stellenwerten.


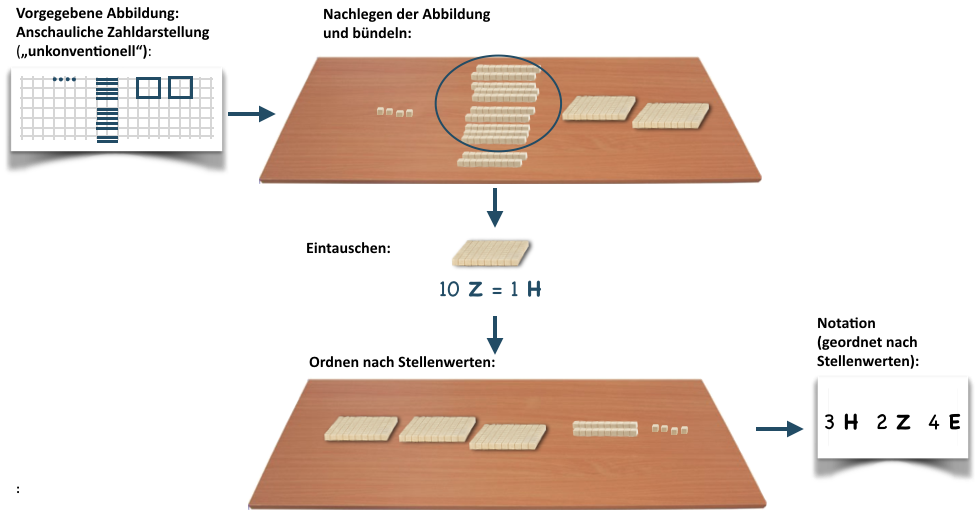
Abbildung 1

nach oben 

Erweiterung des Zahlenraumes (Einbezug der Tausenderstelle)

Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Tausenderbuch, Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB

Die vorgegebenen Zahlenbilder beschränken sich nicht nur auf den Zahlenraum bis 999, sondern beziehen die Tausenderstelle ein.
Analog zur Basisaufgabe legen die Kinder die  Zahlenbilder mit dem Material nach und notieren die dargestellte Zahl auf der Grundlage der Bündelungseinheiten:
(_ Tausender (T), _ Hunderter (H), _ Zehner (Z), _ Einer (E)).

Neben den bereits (nach den Stellenwerten) „geordneten“  Zahlenbildern können auch „ungeordnete“ Zahlenbilder vorgegeben werden.

Tipp: Insbesondere die gedankliche Auseinandersetzung mit „ungeordneten“ oder auch „unkonventionellen“ Zahldarstellungen (vgl. hierzu auch die Aufgabenstellung: 
Ordnen nach Stellenwerten) unterstützt die Entwicklung eines tragfähigen Stellenwertverständnisses. Weitere Informationen hierzu finden Sie in Modul Hintergrund → Das dezimale Stellenwertsystem.
   

Abbildung 2

nach oben 

Notation der anschaulichen Zahldarstellungen (verschiedene Möglichkeiten)

Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB

Analog zur Basisaufgabe werden die abgebildeten Zahldarstellungen (Zahlenbilder) mit dem Material nachgelegt. Anschließend wird die dargestellte Zahl notiert. Hier gibt es 
verschiedene Möglichkeiten:


Abbildung 3

nach oben 

Anwendung der konventionellen Zahlensprechweise

Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB

Beherrschen die Kinder die konventionelle Zahlensprechweise, kann die Übersetzung der Zahlensprechweise in eine anschauliche Zahldarstellung weiter geübt und 
vertieft werden.

Analog zur vertiefenden Aktivität: „Benennen (Verbalisieren) der anschaulichen und schriftlich-symbolischen Zahldarstellungen“ arbeiten die Kinder zu zweit. Eines der 
Kinder nennt eine Zahl (z.B. zweihunderteinunddreißig), das Partnerkind legt die Zahl mit dem gegebenen Material.


Abbildung 4



Alternativ kann die Zahl auch als geschriebenes Zahlwort vorgegeben werden:


Abbildung 5

nach oben 

Systematisches Verändern der vorgegebenen anschaulichen Zahldarstellung (Entbündeln) - Immer 1 E, 1 Z oder 1 H weniger.

Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB

Die Kinder erhalten den Arbeitsauftrag, die gelegte Zahldarstellung systematisch zu verändern (z. B. „Immer 1 Zehner weniger“).
Die Veränderungen in der Zahldarstellung werden dann jeweils dokumentiert (vgl. hierzu auch die verschiedenen Möglichkeiten der Notation - Vertiefung: Dokumentation der 
Zahldarstellungen und Erweiterung: Notation der anschaulichen Zahldarstellungen).

Einen wichtigen Aspekt dieser Aufgabenstellung stellt die Notwendigkeit des Entbündelns dar (vgl. hierzu auch Modul Hintergrund):


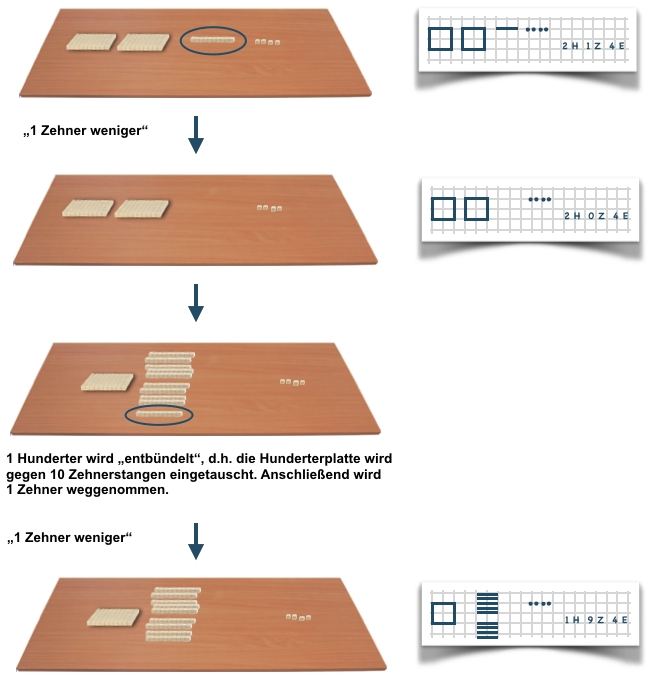
Abbildung 6

Aufgabenvariante: 
Anstatt immer einen 1 E, 1 Z oder 1 H wegzunehmen, kann auch immer 1 E , 1 Z oder 1 H hinzugefügt werden. Für die Kinder kann sich dann die Notwendigkeit ergeben, neu 
bündeln zu müssen.

nach oben