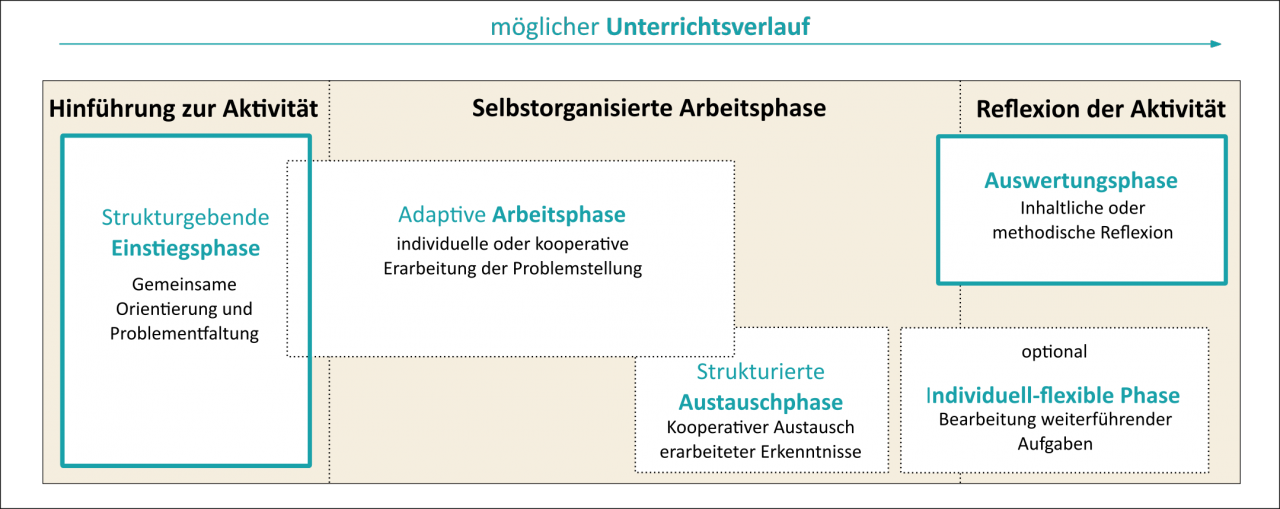
 Abbildung 1 - Möglicher Unterrichtsverlauf
Abbildung 1 - Möglicher Unterrichtsverlauf
Sollen mathematische Gespräche im Klassenverband angeregt werden, ist im Verlauf des Unterrichts besonders die strukturgebende Einstiegsphase und die Auswertungsphase von Bedeutung (Abb.1).
Um dabei die Vorteile der potentiellen Vielfalt von Ideen, Ansätzen und Lösungen nutzen zu können, werden hier, in Anlehnung an Götze und Meyer (2010, 6), vier Handlungsempfehlungen formuliert:
-
Vielfalt vorhersehen
-
Vielfalt zulassen und moderieren
-
Vielfalt gemeinsam ordnen
-
Vielfalt gemeinsam normieren
Grundlage für das kooperativ-kommunikative Lernen (vgl. Brandt & Nührenbörger, 2009) bilden außerdem austauschanregende Aufgaben, die eine gemeinsame Orientierung und Problementfaltung in der strukturgebenden Einstiegsphase erlauben. Die gemeinsame Orientierung im Klassenverband wird durch substantielle Aufgabenformate möglich, die natürliche Differenzierung zulassen (vgl. Wittmann & Müller, 2004; Krauthausen & Scherer, 2014).
Austauschanregende Aufgaben
Aufgabenformate, die die Lernenden dazu befähigen, miteinander in mathematisch-inhaltliche Interaktion zu treten und voneinander zu lernen, sollten verschiedene Merkmale aufweisen. Für den gemeinsamen Austausch im Klassenverband bildet das Aufgabenformat gewissermaßen den didaktischen Rahmen: Eine Aufgabe für alle, die jeder auf seinen Wegen bearbeiten kann und die eine Vielfalt an Herangehensweisen und Diskussionsanlässen fördert, die im gemeinsamen Vorstellen, Ordnen und Systematisieren – im gemeinsamen Austausch – die Heterogenität der Klasse als Mehrwert erfahrbar macht.
Zur Veranschaulichung wird hier das Beispiel „4er-Zahlenketten mit der Zielzahl 20“ gewählt (siehe auch: primakom: Zahlenketten - Einstieg). Das Aufgabenformat „Zahlenketten“ (vgl. z. B. Krauthausen & Scherer, 2014, 301) basiert auf der Fibonacci-Regel: die erste und zweite Startzahl wird frei gewählt, die dritte Zahl wird durch Addition der beiden Startzahlen gewonnen, die Zielzahl entsprechend durch Addition der zweiten Startzahl und der dritten Zahl (Abb. 2).
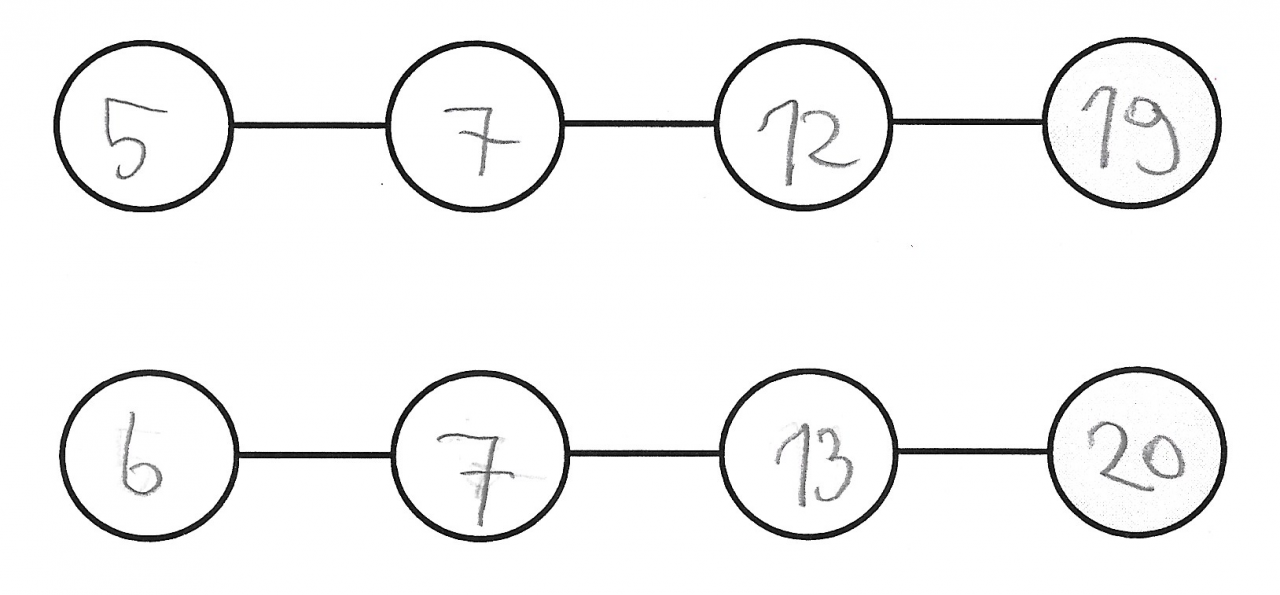 Abbildung 2 - 4er-Zahlenketten
Abbildung 2 - 4er-Zahlenketten
Die Aufgabenstellung könnte lauten: „Finde Zielzahlen, die möglichst nah an der 20 liegen!“. Oder weiter ausdifferenziert (primakom: Zahlenketten - Hintergrund):
-
Finde geschickt möglichst viele Zahlenketten mit der Zielzahl 20!
-
Beschreibe, wie du vorgegangen bist!
-
Hast du alle gefunden? Begründe!
Anregung zur Eigenaktivität: Bearbeiten Sie die Aufgabenstellung! Welche Lösungen könnten Sie von Ihren Schülerinnen und Schülern erwarten? Exemplarische Schülerlösungen und Erklärungen finden sich im Abschnitt „Vielfalt gemeinsam ordnen“ weiter unten auf der Seite.
Für den gemeinsamen Austausch in inklusiven Settings ist dieses Aufgabenformat geeignet, weil
-
die gesamte Lerngruppe das gleiche Lernangebot erhält,
-
die Eingangsschwelle niedrig ist, was „es allen Kindern ermöglicht, einen ersten Zugang zu finden und an einer ihnen möglichen Stelle in eine Auseinandersetzung mit der Sache zu treten“ (Krauthausen & Scherer, 2014, 53),
-
sogenannte „Rampen“ (ebd.) für Leistungsstarke vorhanden sind, wodurch sich das Anspruchsniveau hochregeln lässt („Finde geschickt…“, oder „Hast du alle gefunden?“),
-
die Lernenden in der Bearbeitung ausreichend Freiheitsgrade erhalten, etwa in der Tiefe der Bearbeitung, der Verwendung von Hilfs- oder Arbeitsmitteln, der Art und Weise der Darstellung ihres Vorgehens (vgl. ebd.), die eine individuelle Bearbeitung der Problemstellung ermöglichen und
-
Diskussionsbedarf geschaffen wird,
-
zum einen über die unterschiedlichen Bearbeitungswege, Lösungen und deren Darstellungen, über die Anzahl der Lösungen oder über die Beschreibungen („Beschreibe, wie du vorgegangen bist!“) oder Begründungen („Hast du alle gefunden?“), kurz: durch die potentielle Lösungsvielfalt.
-
Zum anderen deshalb, weil die gesamte Lerngruppe am gleichen Problemkontext gearbeitet hat und so eine Diskussion über die gesammelten Erfahrungen und Erkenntnisse naheliegend ist (anders als bei vereinzelten, individuellen Aktivitäten) (vgl. ebd.).
Vielfalt vorhersehen
Gerade im Kontext von substanziellen Aufgabenformaten und heterogenen Lerngruppen ist es entscheidend, den mathematischen Inhalt, der der Lernaufgabe zugrunde liegt, genau zu kennen. Sonst kann es leicht passieren, dass „die oft kreativen und ungewöhnlichen Lernwege und Argumentationen der Kinder nicht erkannt und in der Folge auch nicht so gewürdigt und eingebunden werden können, wie sie es verdient hätten“ (Krauthausen & Scherer, 2014, 79). Zusätzlich zum sensiblen und diagnostischen Blick der Lehrkraft auf Aussagen und Darstellungen der Lernenden sollten also im Vorfeld mögliche Lösungswege und Herangehensweisen durchdacht und Ergebnisse und Darstellungsweisen produziert werden. Hierzu gehören auch mögliche Fehlvorstellungen oder -strategien (vgl. Götze & Meyer, 2010; zur Antizipation von SchülerInnen-Strategien siehe auch „Zahlenketten mit der Zielzahl 20“ siehe primakom: Zahlenketten - Hintergrund).
Vielfalt zulassen und moderieren
Immer dann, wenn Schülerinnen und Schüler die Möglichkeit erhalten, selbst mathematisch tätig zu werden, stellt dies besondere Herausforderungen an die Rolle der Lehrkraft: Sie muss die aufkommende Vielfalt – und dazu gehören eben auch Fehler, Irrwege, Umwege und Sonderwege zulassen und aushalten (vgl. Götze & Meyer, 2010).
„Den Lernenden alle Steine aus dem Weg zu räumen, mag in guter Absicht geschehen, ist aber keine gute Praxis, denn die Mobilisierung von Kontroversen in fachlichen Diskursen, z.B. durch Anführen von Gegenbeispielen, durch den Aufbau von Widersprüchen und Ähnlichem, ist weitaus lernintensiver und verführt eher zum Nachdenken als die allzu glatt verlaufenden Inszenierungen des Hinterherdenkens.“
(Krauthausen & Scherer, 2014, 86)
Das bedeutet nicht, dass Fehlvorstellungen im Unterricht nicht mehr als solche diskutiert und korrigiert werden sollen, sondern, dass diese Aufgabe nicht ausschließlich der Lehrkraft zufällt. Gerade beim Aufbau grundsätzlicher Vorstellungen stellt der kritische, gemeinsame Diskurs „einen wertvollen und auch notwendigen Baustein mathematischer Lernprozesse dar“ (Nührenbörger, 2007, 245). Dieser Diskurs muss dennoch nicht selten von der Lehrkraft initiiert, aufrechterhalten und gelenkt werden, Hinweise zur Umsetzung finden sich in den Abschnitten „Vielfalt gemeinsam normieren“ und „Fehler ansprechen“ und "Moderation von Plenumsdiskussionen" im Bereich "Unterricht".
Vielfalt gemeinsam ordnen
Damit beim gemeinsamen Austausch im Klassenverband kollektive Lernprozesse angeregt werden können, ist es zunächst wichtig, Tätigkeiten zu finden, die allen Schülerinnen und Schüler der Lerngruppe die aktive Auseinandersetzung mit den Arbeitsergebnissen ermöglicht. „Für den inklusiven Mathematikunterricht ist Ordnen als gemeinsame Tätigkeit besonders geeignet, weil Kinder hier gemeinsam etwas tun“ (Häsel-Weide, 2016, 33). Ordnen als rudimentäre Tätigkeit ist den meisten Kindern bekannt (vgl. ebd.), das gemeinsame Ordnen ist dennoch anspruchsvoller, da die Lernenden gezwungen sind, sich auf die Lösungen ihrer Mitschülerinnen und Mitschüler einzulassen und sich darüber verständigen müssen, wie geordnet werden soll.
Das Ordnen stellt aber keinen Selbstzweck dar, sondern erfüllt sowohl im Unterrichtsgeschehen als auch im Lernprozess der Kinder verschiedene Funktionen, die hier kurz erläutert und im Anschluss beispielhaft illustriert werden:
1.
Beim Ordnen im Klassenverband werden die Lösungen und Arbeitsergebnisse der Lernenden gesammelt, für andere sichtbar und damit für den weiteren Reflexionsprozess zugänglich gemacht. Hilfreich sind hierfür Materialien und Darstellungsweisen, die dieses zulassen. Beispielsweise können die Lernenden gebeten werden, aus ihren Lösungen einige wenige auszuwählen, die sie noch einmal „in groß“ auf ein neues Blatt schreiben (siehe Material), alternativ kann auch die Lehrkraft Schülerlösungen auswählen, um sie mit in die nächste Stunde zu nehmen
2.
Der Ordnungsprozess schafft Diskussionsbedarf über die Kriterien der gemeinsamen Ordnung. Die Kinder lernen dabei mathematische Merkmale „zu formulieren, Kriterien einzuhalten, zu vergleichen und passende Elemente zu finden“ (ebd., 33). Die vielfältigen Lösungen und Arbeitsergebnisse werden dabei im sozialen Diskurs systematisiert, kommentiert und in Beziehung zu einander gesetzt.
Da solche gemeinsamen Ordnungsprozesse von allein in der Klasse laufen können, aber nicht müssen, ist es wichtig, dass die Lehrkraft darauf vorbereitet ist, die Diskussion – auch inhaltlich – zu moderieren, zu lenken und Impulse zu geben. Sie muss sich zum Beispiel darüber im Klaren sein, welche Möglichkeiten für Ordnungskriterien es gibt und welche entsprechenden Impulse sie geben kann. Der Umgang mit Ordnungskriterien ohne mathematischen Gehalt („bunt geschrieben vs. mit Bleistift“) sollte ebenso bedacht werden.
3.
Am Ende eines solchen Ordnungsprozesses können dem Problemkontext zugrundeliegende fundamentale Strukturen herausgearbeitet werden. Dies muss aber nicht notwendigerweise Ziel des Ordnungsprozesses sein. Bedingung ist, dass das gemeinsame Lernangebot hinreichend komplex ist (siehe Austauschanregende Aufgaben), um eine Ordnung nach arithmetischen Kriterien zuzulassen, und diese Kernstruktur auch von möglichst vielen Lernenden erfasst werden kann (vgl. Häsel-Weide, 2016). Zusätzlich sollten auch die Impulse der Lehrkraft die mathematische Struktur fokussieren.
Bezogen auf das Aufgabenbeispiel „4er-Zahlenketten mit der Zielzahl 20“ lässt sich dies folgendermaßen veranschaulichen:
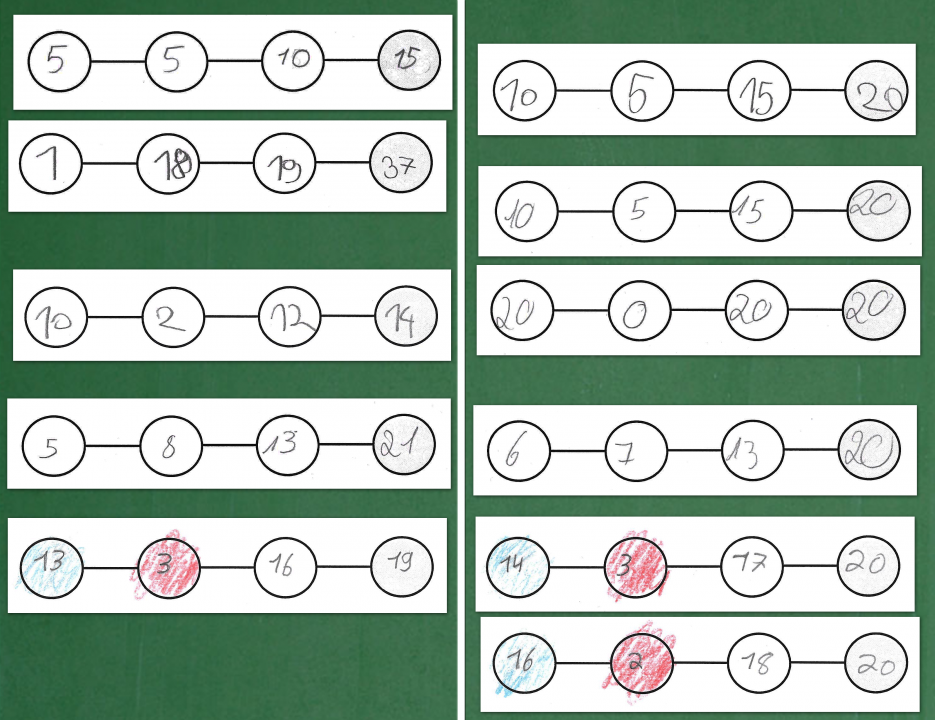 Abbildung 3 - Zahlenketten mit und ohne Zielzahl 20
Abbildung 3 - Zahlenketten mit und ohne Zielzahl 20
Zu 1.: An der Tafel werden die Zettel mit den Arbeitsergebnissen der Kinder gesammelt, die groß genug sind, um sie im Sitzkreis noch erkennen zu können und die nach Bedarf verschoben werden können.
Zu 2.: Das Ordnungskriterium ist „Zielzahl 20 getroffen“ vs. „Zielzahl 20 nicht getroffen“. Das Kriterium ist naheliegend, relativ einfach für die Lernenden umzusetzen und verschafft einen guten Überblick über die Lösungen. Interessant wäre nun, die rechte Seite (Zielzahl 20 wurde getroffen) genauer in den Blick zu nehmen und weiter zu ordnen. Mögliche Kriterien könnten „gleiche Zahlenketten“ (wie oben rechts, Startzahlen „10“ und „5“) oder „Startzahlen systematisch verändert (unten rechts) sein. Auch ein Blick auf die linke Seite lohnt, hier ist zum Beispiel das Kriterium „Zielzahl 20 knapp verpasst“ interessant, da sich durch Probieren oder systematisches Verändern leichter „passende“ Startzahlen ableiten lassen.
Trotzdem - und dieser Punkt ist entscheidend – geht es nicht nur darum, Ordnungskriterien zu nennen oder zu diskutieren, sondern auch darum, eigene oder fremde Lösungen ein- und zuzuordnen, oder zu bestehenden Ordnungen neue Elemente zu finden. Im Ordnungsprozess sind also ganz unterschiedliche Tätigkeiten denkbar, zu denen die Lernenden angeregt werden können.
Zu 3.: Die zugrundeliegende Struktur, die zusätzlich entdeckt werden kann, ist die, dass eine Veränderung der zweiten Startzahl „doppelt“ in der Zielzahl „ankommt“, während eine Veränderung der ersten Startzahl „einzeln“ oder „unverändert“ in der Zielzahl „ankommt“ (siehe Tabelle 1).
Tabelle 1 - 4er-Zahlenketten
|
1. Startzahl |
2. Startzahl |
|
Zielzahl |
|
4 |
8 |
12 |
20 |
|
2 |
10 |
12 |
22 |
|
a |
b |
a+b |
a+2b |
Diese Erkenntnis kann bspw. genutzt werden, um Strategien, wie etwa das gegensinnige Verändern zu entwickeln. Die farbig markierten Zahlenketten (die letzten beiden Zeilen in Abbildung 3) zeigen ein solch systematisches Vorgehen. Die komplette Schülerlösung ist in Abbildung 4 zu sehen, in der der Schüler auch seine Strategie beschrieben hat („erste Startzahl +2, zweite Startzahl -1“).
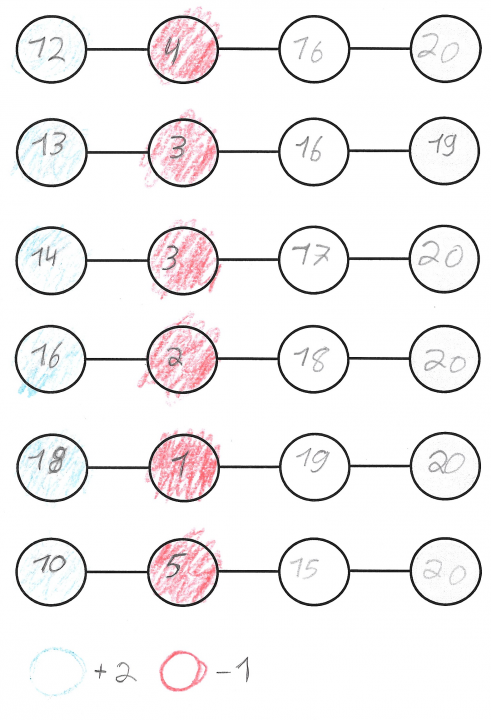 Abbildung 4 - Systematische Schülerlösung
Abbildung 4 - Systematische Schülerlösung
Vielfalt gemeinsam normieren
Eng mit der Tätigkeit des Ordnens verbunden ist das Normieren von Vielfalt (vgl. Götze & Meyer, 2010). „Jedes Kind konstruiert für sich selbst eigene Sinndeutungen über mathematische Zusammenhänge. Zugleich handelt es diese aber stets mit anderen Kindern oder der Lehrpersonen innerhalb der Kultur des Mathematikunterrichts aus.“ (Nührenbörger, 2007, 245). Dies ist notwendig, weil sich mathematische Begriffe (im Sinne tragfähiger Grundvorstellungen) „kulturhistorisch entwickelt [haben] und daher auch kultureller Prozesse – das heißt Prozesse der Kommunikation und Interaktion – [bedürfen], um entwickelt und gelernt zu werden“ (Schülke & Söbbeke, 2010, 21). Diesen Prozessen muss im Mathematikunterricht genügend Raum gegeben werden. Unterstützt werden können sie durch die professionelle Moderation der Lehrkraft in Phasen des gemeinsamen Austausches. Entscheidend dabei ist, den Fokus der Lernenden im Austausch immer wieder bewusst auf diese Prozesse des „Aushandelns von Bedeutung“ (Bauersfeld, 2002, 12) zu lenken und Argumentationen einzufordern, sowohl zu Begriffen und Vorstellungen als auch zu Lösungen und Lösungswegen.
Sich darüber verständigen, wie etwas heißt und was es bedeutet (vgl. Schütte, 2002):
Im Mathematikunterricht der Grundschule wird bereits eine große Anzahl mathematischer Fachbegriffe verwendet, „Mathematik wird daher häufig als erste Fremdsprache bezeichnet“ (ebd., 16). Wichtig ist dabei, dass Kinder sich mit dem Begriffsinhalt auseinandersetzen können, bevor Fachbegriffe eingeführt werden, damit der zugehörige Verstehenskontext gesichert ist (vgl. ebd.). Empfehlenswert ist ein Klassenwortspeicher, der gemeinsam geführt wird und in welchem Begriffe festgehalten werden, deren Bedeutungsrahmen kollektiv abgeklopft, kontrastiert und assoziiert wurde (vgl. ebd.).
Sich auf richtige Lösungen und geschickte Lösungswege verständigen (vgl. Götze & Meyer, 2010):
Im Mathematikunterricht kommt es „letztlich auch auf korrekte Ergebnisse und geschickte Lösungswege an“ (ebd., 7), es darf – besonders für die Schülerinnen und Schüler – nicht der Eindruck entstehen, „einfach nur ‚irgendetwas‘ zu machen“ (ebd., 8). Vielfalt muss normiert werden, um es den Lernenden einfacher zu machen, sinnvolle, hilfreiche neue Verfahren oder Herangehensweisen herauszufiltern. Diese sollen aber eben am Ende der Stunde nicht einfach genannt werden, sondern sich im Verlauf des gemeinsamen Austausches entwickeln. Die Lehrkraft muss natürlich durch ihre Vorbereitung schon wissen, in welche Richtung die Reise gehen könnte.
Im Folgenden werden im Unterrichtsteil konkrete Hinweise zur Moderation von Plenumsdiskussionen, zu Gesprächsregeln und zu Methoden des gemeinsamen Austausches gegeben.