Abbildung 1: Übersicht_Aufgabenstellung kompakt "Zahlen zerlegen"
Download Übersicht
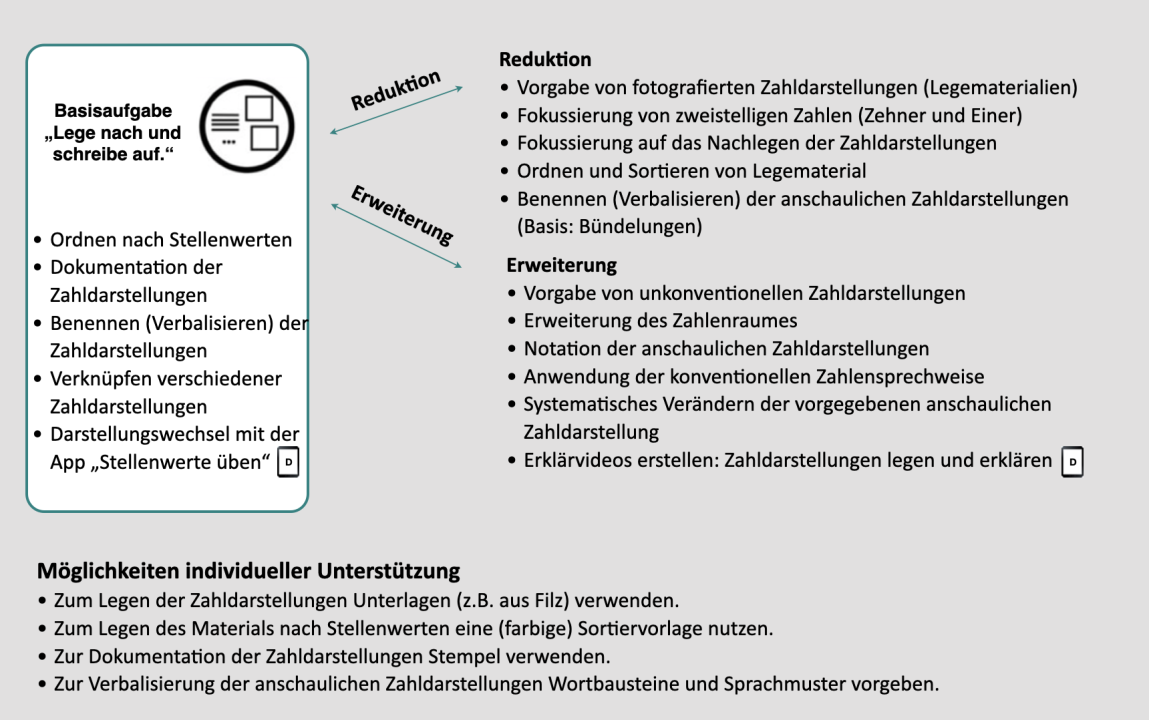
Basisaufgabe
"Lege nach und schreibe auf."
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Vorgegeben werden verschiedene Abbildungen (Zahlenbilder).
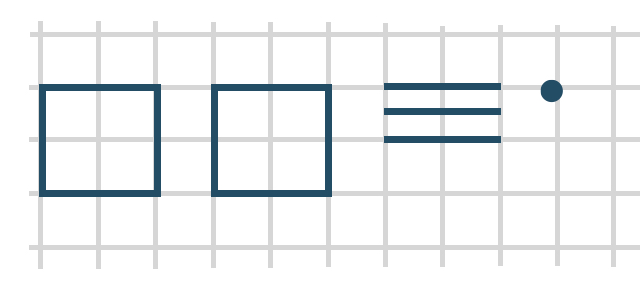Abbildung 2
Als Legematerial erhalten die Kinder Mehrsystemblöcke (Dienes-Material).
Abbildung 3
Alternativ arbeiten sie mit Hunderterpunktefeldern, Zehnerstreifen und Wendeplättchen.
Abbildung 4
Die abgebildeten Zahldarstellungen werden mit dem Material nachgelegt; anschließend wird die dargestellte Zahl auf der Grundlage der Bündelungseinheiten notiert:
X Hunderter H, Y Zehner Z, Z Einer E
Wichtig (Zahldarstellungen zeichnen und deuten):
Damit die Kinder diese abstrahierte Zahldarstellung (Quadrat, Strich und Punkt)
deuten können, müssen im Vorfeld Übungen zum Zeichnen und Deuten von
Zahlenbildern durchgeführt werden:
Abbildung 5
Bei den Abbildungen gibt es neben bereits (nach Hundertern, Zehnern und Einern/ nach den Stellenwerten) "geordneten“ Zahldarstellungen auch Abbildungen von "ungeordneten" Zahldarstellungen.
Insbesondere die gedankliche Auseinandersetzung mit "ungeordneten" oder auch "unkonventionellen" Zahldarstellungen unterstützt die Entwicklung eines tragfähigen Stellenwertverständnisses. Weitere Informationen hierzu finden Sie unter Hintergrund: Dezimalsystem.
Geordnete Zahldarstellungen:
Vorgegeben werden sollten auch Zahlenbilder, bei denen beispielsweise kein Einer (oder Hunderter bzw. Zehner) vorgegeben ist.
Die Kinder legen die vorgegebene Abbildung mit Material nach und notieren die Anzahl der Hunderter, Zehner und Einer.
Abbildung 6
Ungeordnete Zahldarstellungen:
Die Kinder legen das vorgegebene „ungeordnete“ Zahlenbild - möglichst bereits nach Stellenwerten geordnet - mit Material nach.
Abbildung 7
Im Vordergrund dieser Aufgabenstellung steht die Identifizierung und Unterscheidung von Einerwürfeln, Zehnerstangen und Hunderterplatten.
Bestimmt und notiert wird die jeweilige Anzahl der gelegten Einerwürfel (E), Zehnerstangen (Z) und Hunderterplatten (H).
Wichtig:
Ordnet ein Kind das Material nicht nach Stellenwerten geordnet an, sollte dieses durch die Lehrkraft angeregt werden (vgl. hierzu die Vertiefung "Ordnen nach Stellenwerten") Unterstützend kann auch eine Sortierunterlage (vgl. hierzu die Möglichkeiten individueller Unterstützung) eingesetzt werden.
In Bezug auf die Notation der Zahl gibt es verschiedene Möglichkeiten:
Die Kinder notieren sowohl die Anzahl der gegebenen Hunderter, Zehner und Einer als auch die Angaben H, Z und E selbständig:
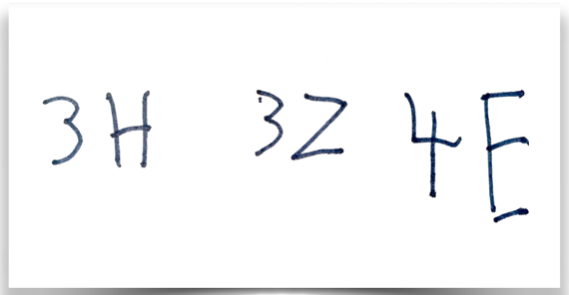Abbildung 8
Auf einem Arbeitsblatt werden die Bündelungseinheiten (Hunderter, Zehner, Einer) nach Stellen geordnet vorgegeben.
Abbildung 9
Die Kinder notieren die Anzahl der „Bündel“ (Hunderterplatten, Zehnerstangen und Einerwürfel).
Abbildung 10
Möglich ist auch, für die Notation jeder Bündelungseinheit einen eigenen Zettel zur Verfügung zu stellen. Durch den Auftrag, diese zu sortieren, werden die Kinder zusätzlich herausgefordert, über die Abfolge der Stellenwerte in einer Zahl nachzudenken.
Die Notation kann auch farbig erfolgen:
Abbildung 11
Unterstützend kann die Notation auch farbig erfolgen. So werden beispielsweise in der Montessori-Pädagogik die Farben grün, rot und blau zur Repräsentation der Stellenwerte bei der Zahldarstellung genutzt.
Bei der Identifizierung der einzelnen Stellen und der Unterscheidung der Stellenwerte kann die „Färbung“ der Stellenwerte zunächst eine Hilfe sein (vgl. hierzu auch die Möglichkeiten individueller Unterstützung - Einsatz einer dreifarbigen Sortierunterlage).
Wichtig:
Zu einem späteren Zeitpunkt muss die Ablösung von einer farbigen Unterscheidung der Stellenwerte erfolgen.
Geschieht dies nicht, besteht die Gefahr, dass die Zuordnung zu Stellen bzw. die Anordnung der Stellenwerte einzig auf der Grundlage einer (gelernten und auswendig gewussten) Farbfolge erfolgt.
Vertiefung
Ordnen nach Stellenwerten
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
In der vertiefenden Aktivität "Ordnen nach Stellenwerten" stehen "ungeordnete“ Zahldarstellungen im Vordergrund.
Ordnen die Kinder während der Bearbeitung der Basisaufgabe die Mehrsystemblöcke nicht direkt nach Stellenwerten, erhalten sie den zusätzlichen Arbeitsauftrag, die Mehrsystemblöcke zu ordnen und nach Stellenwerten geordnet zu notieren.
Wichtig:
Bei den vorgegebenen Abbildungen sollte die Reihenfolge, in der die Einer, Zehner und Hunderter dargeboten werden, immer wieder wechseln (d.h. gegeben werden „geordnete" und „ungeordnete" Darstellungen).
Wird den Kindern das Material immer nur in bereits geordneter Reihenfolge angeboten, ist ein Nachdenken über die Notation von Zahlen und die Abfolge der Stellenwerte in einer Zahl unnötig.
Allerdings soll die Überlegung, an welche Stelle die Anzahl der Zehner, die Anzahl der Einer oder die Anzahl der Hunderter notiert wird, dem Kind gerade nicht erspart bleiben, denn gerade auf das Wissen um die Bedeutung der Stelle, an der eine Ziffer steht, kommt es an.
Beispiel:
Abbildung 13
Vertiefung
Dokumentation der Zahldarstellungen
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Werden den Kindern „ungeordnete“ oder auch „unkonventionelle“ Zahldarstellungen vorgegeben, ist es sinnvoll, das neu geordnete Legematerial zu dokumentieren, indem die Kinder ein Zahlenbild zeichnen und die Zahl notieren.
Abbildung 14
Das Übertragen einer mit Material gelegten Zahldarstellung in eine gezeichnete Zahldarstellung (Zahlenbild) stellt zugleich wieder eine Übersetzung von Zahlrepräsentationen innerhalb einer Repräsentationsebene (anschauliche Zahldarstellungen) dar.
Ausführliche Hintergrundinformationen zur Bedeutung von „Übersetzungen“ (innerhalb einer Repräsentationsebene und zwischen Zahldarstellungen unterschiedlicher Repräsentationsebenen) für den Aufbau eines tragfähigen Stellenwertverständnisses finden Sie unter Hintergrund: Dezimalsystem.
Vertiefung
Benennen (Verbalisieren) der Zahldarstellungen
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Wesentlich ist auch die sprachliche Begleitung der vorgenommenen Handlungen und das Benennen (Verbalisieren) der Zahldarstellungen:
An dieser Stelle wird zunächst bewusst auf die konventionelle Benennung der Zahlen (wie z.B. zweihunderteinunddreißig) verzichtet.
Stattdessen wird von Hundertern, Zehnern und Einern gesprochen (z. B. vier Zehner, drei Einer), denn „für die Erarbeitung von Einsicht in das Bündelungsprinzip ist es nicht erforderlich und vermutlich auch wenig hilfreich, zugleich schon auf die Irregularitäten der Zahlwortbildung einzugehen“ (Gaidoschik 2015, S. 178).
Weitere Hintergrundinformationen und Erläuterungen zu einer Erarbeitung der Zahlensprechweise und dem Lesen und Schreiben von Zahlen (als Ziffernfolge) finden Sie unter Hintergrund: Dezimalsystem.
Beherrschen Kinder bereits die konventionelle Zahlensprechweise, dann können sie selbstverständlich die Zahlen auch so benennen. Dennoch ist es auch dann sinnvoll, zwischen den verschiedenen Möglichkeiten, Zahlen zu bezeichnen, zu wechseln und über Bezeichnungen und Sprechweisen nachzudenken.
Aufgabenstellung:
Das Benennen und Verbalisieren der Zahlenbilder bzw. Zahldarstellungen kann auch in einer konkreten Aufgabenstellung erfolgen:
Die Kinder arbeiten zu zweit. Eines der beiden Kinder nennt die Anzahl der Hunderter, Zehner und Einer, das andere Kind legt das entsprechende Legematerial. Die Angabe der Hunderter, Zehner und Einer kann auch ungeordnet erfolgen. Das Partnerkind hat dann zugleich die Aufgabe, das Legematerial geordnet zu legen.
Abbildung 15
Vertiefung
Verknüpfen verschiedener Zahldarstellungen ("übersetzen")
Material: Vorlage zum Zuordnen / verschiedene Zahldarstellungen
Die Kinder erhalten Karten mit verschiedenen Zahldarstellungen (anschauliche, schriftlich-symbolische und verbal-symbolische Zahldarstellungen) und ordnen zueinander passende Darstellungen auf einer Vorlage zum Zuordnen an.
Der Fokus liegt hier auf der Verknüpfung bzw. Zuordnung von Repräsentanten einer Darstellungsebene bzw. zwischen verschiedenen Darstellungsebenen. Ausführliche Hintergrundinformationen hierzu finden Sie unter Modul: Hintergrund: Dezimalsystem.
Variiert werden können - je nach Zielsetzung und den jeweiligen Lernvoraussetzungen der Kinder - die Darstellungen und die Anzahl der Darstellungen, die den Kindern zur Verfügung gestellt werden.
Wobei der Schwerpunkt dieser Aufgabenstellung - im Sinne einer Vertiefung der Basisaufgabe - zunächst in der Verknüpfung von anschaulichen und schriftlich-symbolischen Darstellungen liegen sollte.
Gleichzeitig können und sollten die Zuordnungen sprachlich begleitet und begründet werden, z.B.:
"Die Karten passen zueinander. Auf der einen Karte sind drei Hundertertafeln, zwei Zehnerstangen und vier Einerwürfel. Auf der anderen Karte steht: drei Hunderter, zwei Zehner, vier Einer."
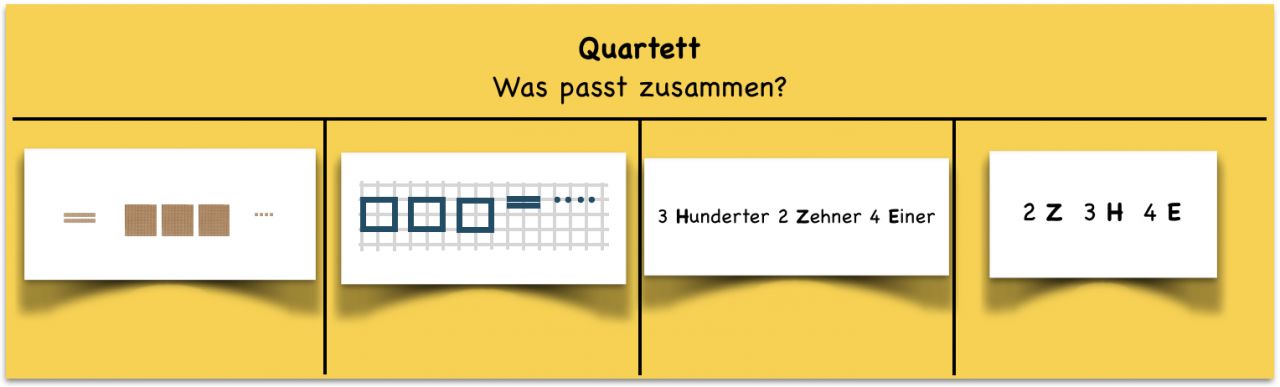Abbildung 16
Eine Auswahl möglicher Zahldarstellungen:
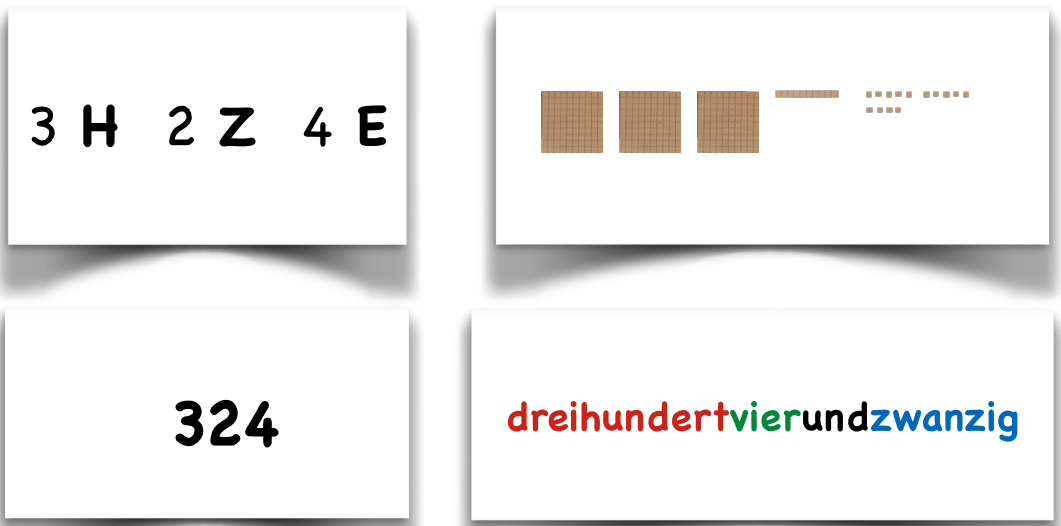Abbildung 17
Vertiefung
Darstellungswechsel mit der App Stellenwerte üben
Die Tablet-App Stellenwerte üben (verfügbar auf iOS-Geräten, Stand Oktober 2024) kann in Übungsphasen zum Stellenwertverständnis ergänzend zu den oben aufgeführten Aufgabenstellungen eingesetzt werden. Das Ziel ist, das Stellenwertverständnis zu festigen, nachdem eine Erarbeitung und Entwicklung des Stellenwertverständnisses im Mathematikunterricht erfolgt ist. Ausführliche Informationen zu der App finden Sie bei PIKAS digi und im Didaktischen Kommentar für Lehrerinnen und Lehrer.
Die App nutzt zur Anschauung digitales Zehnersystemmaterial (auch bekannt als Dienes-Material oder Mehrsystemblöcke), welches in einer Sortiertafel mit den Repräsentanten Einer, Zehner und Hunderter gelegt werden kann. Die Stellenwerttafel kann im Zahlenraum bis 100 oder bis 1000 genutzt werden. Vielfältige Aktivitäten und Handlungen am digitalen Material sind in acht Übungsformaten (differenziert in zwei Grundlagen- und sechs Übersetzungsmodule) möglich, die den Darstellungswechsel zwischen Menge, Zahlwort und Zahlzeichen wechselweise realisieren. Diese werden in der nachfolgenden Tabelle in einem Überblick über die Übungsformate der App Stellenwerte üben vorgestellt.
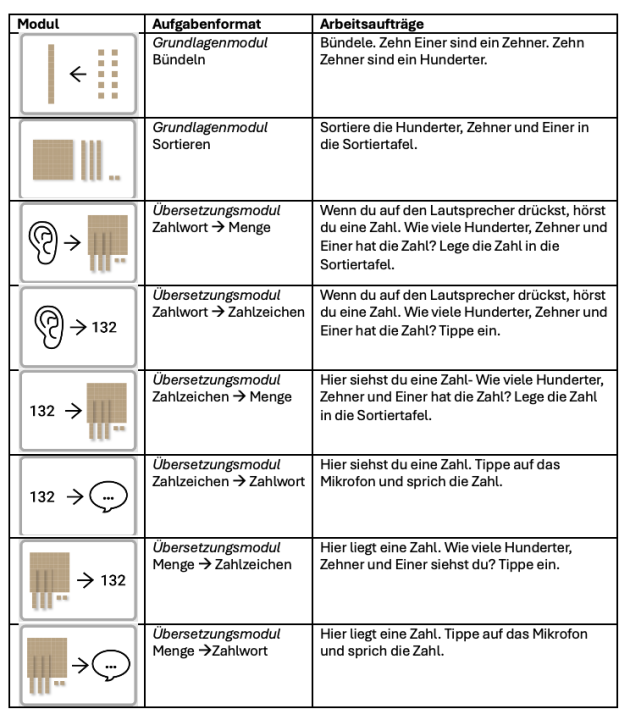Abbildung 18
Die Auswahl der Übungsformate kann je nach Bedarf der Lernenden ganz individuell erfolgen. Zu jeder Aufgabe erhalten die Schüler:innen direktes Feedback. Teilweise geht das Feedback auch über ein „richtig“ oder „falsch“ hinaus und die Kinder erhalten kurze informative Rückmeldungen, wie z. B. „zu wenig“, wenn noch weitere Zehner, Einer oder Hunderter gelegt werden müssen, um eine Zahl darzustellen, oder „weiter bündeln“, wenn mehr als 9 Zehner oder 9 Einer in einer Spalte liegen und diese noch weiter zusammengefasst werden können.
Zur sprachlichen Unterstützung liest die App vor jeder Übung die Arbeitsaufträge vor (z. B. „Wenn du auf den Lautsprecher drückst, hörst du eine Zahl. Wie viele Hunderter, Zehner und Einer hat die Zahl? Lege die Zahl in die Sortiertafel.“). Außerdem können Kinder in zwei Übungsformaten bei der Übersetzung von der Menge bzw. dem Zahlzeichen in das Zahlwort ihre Lösungen einsprechen und überprüfen lassen.
Video: Einblicke in die App Stellenwerte üben
Bei einigen Übungsformaten müssen komplexe motorische Handlungen beim Bündeln am Tablet durchgeführt werden. Beispielsweise werden jeweils zehn eng beieinanderliegende Plättchen oder Zehnerstangen eingekreist und anschließend per Knopfdruck verschoben. Dabei könnte es bei einigen Kindern zu Schwierigkeiten in der Feinmotorik und Touch-Bedienung kommen – ein Tablet-Stift kann hier eine Unterstützungsmöglichkeit darstellen.
Reduktion
Vorgabe von fotografierten Zahldarstellungen (Legematerialien)
Material: Fotografien von Zahldarstellungen (Mehrsystemblöcke, Hunderterpunktefelder, Zehnerstreifen, Wendeplättchen), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Analog zur Basisaufgabe erhalten die Kinder verschiedene Abbildungen von Zahldarstellungen und als Legematerial Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen.
Bei den vorgegebenen Abbildungen handelt es sich allerdings nicht um abstrahierte Zahldarstellungen (Zahlenbilder), bei denen Hunderter durch ein Quadrat, Zehner durch einen Strich und Einer durch einen Punkt dargestellt werden, sondern um Fotografien der konkreten Materialien. Hierdurch kann der Übersetzungsprozess (Abbildung → gelegtes Material) unterstützt und vereinfacht werden.
Abbildung 19
Reduktion
Fokussierung auf zweistellige Zahlen (Zehner und Einer)
Material: versch. Abbildungen (Zahldarstellungen), Legematerial (Mehrsystemblöcke oder Zehnerstreifen und Wendeplättchen), AB
Analog zur Basisaufgabe erhalten die Kinder verschiedene Abbildungen (Zahlenbilder) und als Legematerial Mehrsystemblöcke (Dienes-Material) oder Punktefelder, allerdings beschränkt auf den Zahlenraum bis 99.
Beispiele für mögliche Zahldarstellungen („geordnete“ und „ungeordnete“ Darstellungen):
Abbildung 20
Reduktion
Fokussierung auf das Nachlegen der Zahldarstellungen
Material: Abbildungen Zahldarstellungen, Legematerial (Mehrsystemblöcke, Zehnerstreifen, Wendeplättchen), AB
Die Aufgabenstellung wird beschränkt auf das Nachlegen der vorgegebenen Abbildungen (Zahlenbilder oder Fotografien).
Abbildung 21
Reduktion
Ordnen und Sortieren von Legematerial
Material: Legematerial (Mehrsystemblöcke, Zehnerstreifen, Wendeplättchen)
Gegeben werden den Kindern beispielsweise mehrere Hunderterplatten, Zehnerstangen und Einerwürfel (unsortiert). Die Aufgabenstellung besteht darin, dass Material zu sortieren und zu ordnen:
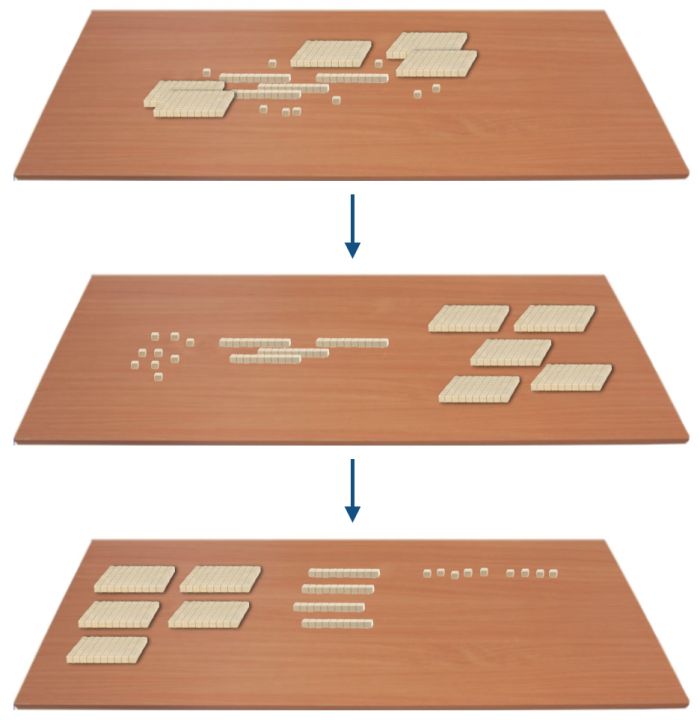Abbildung 22
Reduktion
Benennen (Verbalisieren) der anschaulichen Zahldarstellungen (Basis Bündelungen):
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Zeigen Kinder Schwierigkeiten und Unsicherheiten bei der Verbalisierung der Zahlen (z.B. in Zahlendrehern) sollte bei der Erarbeitung des Bündelungsprinzips konsequent auf die Sprechweise X Hunderter, Y Zehner und Z Einer geachtet werden (vgl. hierzu auch Basisaufgabe und Vertiefung: Benennen (Verbalisieren) der Zahldarstellungen).
Weitere Hintergrundinformationen zu den Schwierigkeiten und Hürden beim Erwerb eines tragfähigen Stellenwertverständnisses, die sich für Kinder durch die Zahlwortbildung im deutschen Sprachraum ergeben sowie Erläuterungen zu einer Erarbeitung der Zahlensprechweise finden Sie in Modul Hintergrund: Dezimalsystem.
Reduktion
Verknüpfen ausgewählter Zahldarstellungen ("übersetzen")
Material: Vorlage zum Zuordnen / verschiedene Zahldarstellungen
Während bei der vertiefenden Aufgabenstellung "Verknüpfen verschiedener Zahldarstellungen" zugleich mehrere Darstellungen einander zugeordnet werden sollen, liegt der Schwerpunkt dieser Aufgabenstellung im Bereich Reduktion auf der Zuordnung von jeweils zwei (ausgewählten) Zahldarstellungen.
Die Auswahl der eingesetzten Zahldarstellungen ist abhängig von den individuellen Lernvoraussetzungen der Kinder. Da insbesondere die Deutung von „ungeordneten“ Zahldarstellungen von Bedeutung ist, kann es sinnvoll sein, hier gezielt ungeordnete und geordnete Zahldarstellungen einander zuordnen zu lassen.
Abbildung 23
Weitere mögliche Zuordnungen:
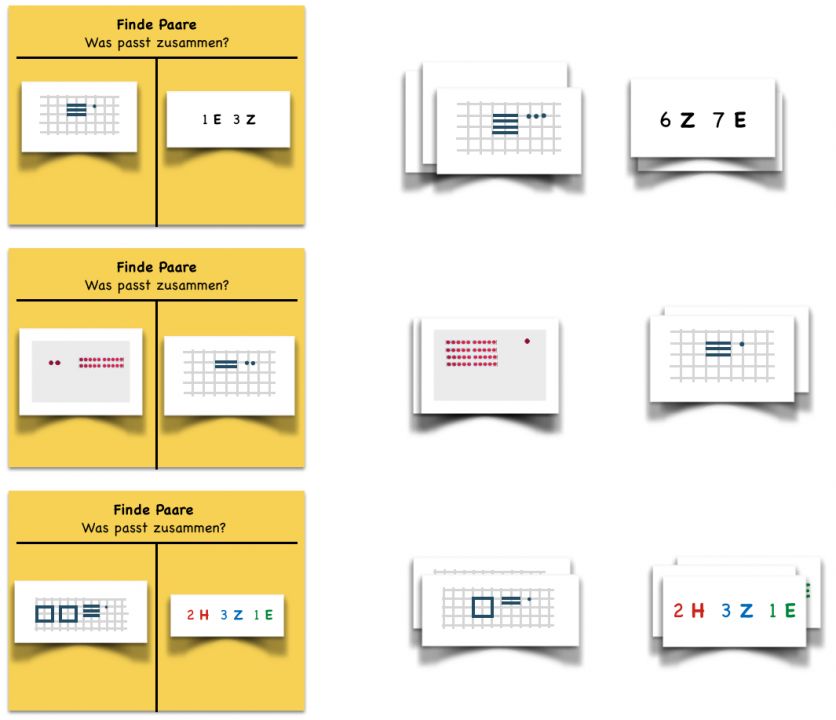Abbildung 24
Erweiterung
Vorgabe von unkonventionellen Zahldarstellungen
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Analog zur Aufgabenstellung „Lege nach und schreibe auf“ (Basisaufgabe) legen die Kinder bei dieser Aufgabenstellung der Erweiterung Zahlenbilder mit Legematerial nach und notieren die Zahldarstellung.
Im Gegensatz zur Basisaufgabe stehen im Vordergrund der Erweiterung allerdings „unkonventionelle“ Zahldarstellungen mit beispielsweise 2 Hunderterplatten,
12 Zehnerstangen und 4 Einerwürfeln.
Die Kinder legen das vorgegebene Zahlenbild nach, werden angeregt, weiter zu bündeln („Immer zehn bündeln“) und ordnen das Material nach Stellenwerten.
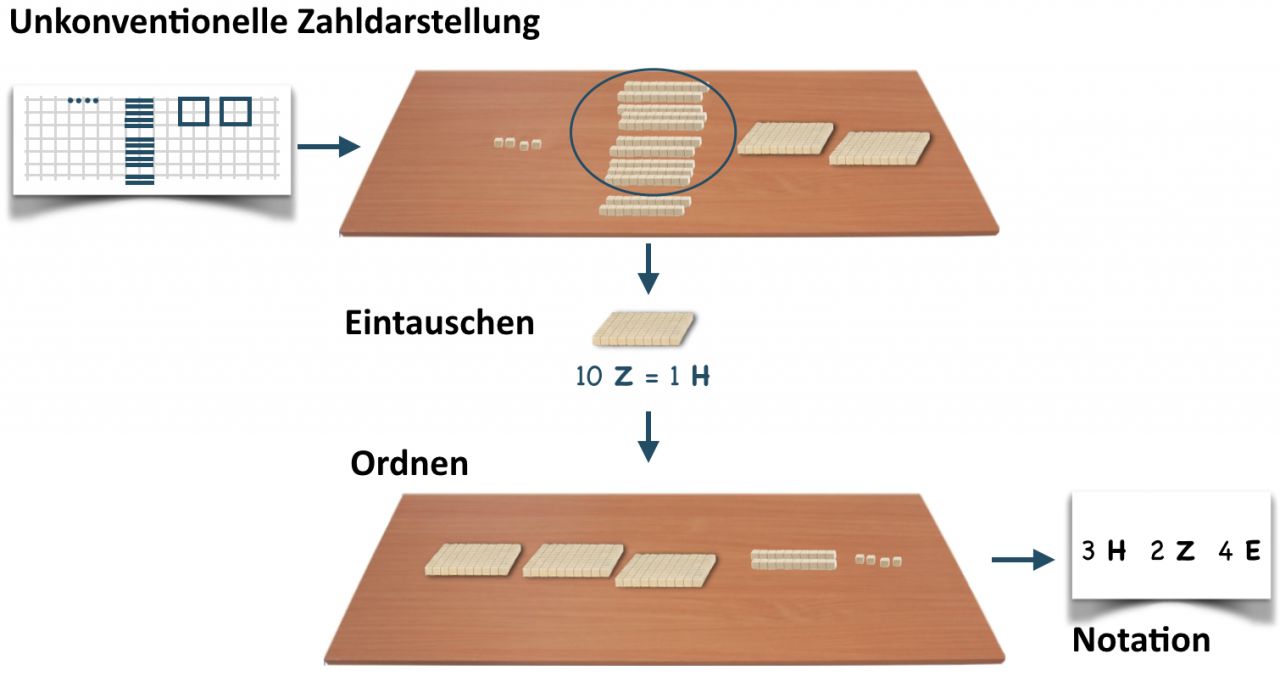Abbildung 25
Erweiterung
Erweiterung des Zahlenraumes (Einbezug der Tausenderstelle)
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Tausenderbuch, Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Die vorgegebenen Zahlenbilder beschränken sich nicht nur auf den Zahlenraum bis 999, sondern beziehen die Tausenderstelle ein. Analog zur Basisaufgabe legen die Kinder die Zahlenbilder mit dem Material nach und notieren die dargestellte Zahl auf der Grundlage der Bündelungseinheiten (Tausender (T), Hunderter (H), Zehner (Z), Einer (E)).
Abbildung 26
Neben den bereits (nach den Stellenwerten) "geordneten" Zahlenbildern können auch "ungeordnete" Zahlenbilder vorgegeben werden.
Insbesondere die gedankliche Auseinandersetzung mit "ungeordneten" oder auch "unkonventionellen" Zahldarstellungen unterstützt die Entwicklung eines tragfähigen Stellenwertverständnisses. Weitere Informationen hierzu finden Sie in Modul Hintergrund: Dezimalsystem
Abbildung 27
Erweiterung
Notation der anschaulichen Zahldarstellungen (verschiedene Möglichkeiten)
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Analog zur Basisaufgabe werden die abgebildeten Zahldarstellungen (Zahlenbilder) mit dem Material nachgelegt. Anschließend wird die dargestellte Zahl notiert. Hier gibt es verschiedene Möglichkeiten:
Abbildung 28
Erweiterung
Anwendung der konventionellen Zahlensprechweise
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Beherrschen die Kinder die konventionelle Zahlensprechweise, kann die Übersetzung der Zahlensprechweise in eine anschauliche Zahldarstellung weiter geübt und vertieft werden.
Analog zur vertiefenden Aktivität: „Benennen (Verbalisieren) der anschaulichen und schriftlich-symbolischen Zahldarstellungen“ arbeiten die Kinder zu zweit. Eines der Kinder nennt eine Zahl (z.B. zweihunderteinunddreißig), das Partnerkind legt die Zahl mit dem gegebenen Material.
Abbildung 29
Alternativ kann die Zahl auch als geschriebenes Zahlwort vorgegeben werden:
Abbildung 30
Erweiterung
Systematisches Verändern der vorgegebenen anschaulichen Zahldarstellung - Immer 1 E, 1 Z oder 1 H weniger.
Material: versch. Abbildungen (Zahlenbilder), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), AB
Die Kinder erhalten den Arbeitsauftrag, die gelegte Zahldarstellung systematisch zu verändern (z. B. „Immer 1 Zehner weniger“). Die Veränderungen in der Zahldarstellung werden dann jeweils dokumentiert.
Einen wichtigen Aspekt dieser Aufgabenstellung stellt die Notwendigkeit des Entbündelns dar.
1 Zehner weniger:
Um einen weiteren Zehner wegnehmen zu können, muss ein Hunderter "entbündelt“ werden, d.h. die Hunderterplatte wird gegen 10 Zehnerstangen eingetauscht.
1 Zehner weniger:
Abbildung 31
Aufgabenvariante:
Anstatt immer einen 1 E, 1 Z oder 1 H wegzunehmen, kann auch immer 1 E , 1 Z oder 1 H hinzugefügt werden. Für die Kinder kann sich dann die Notwendigkeit ergeben, neu bündeln zu müssen.
Erweiterung
Erklärvideo erstellen: Zahldarstellungen legen und erklären
Material: Stellenwerttafel, Legematerial (Mehrsystemblöcke oder Hunderterfeld, Zehnerstreifen, Fünferstreifen und Einerplättchen), Tablet
Die Schüler:innen planen und filmen gemeinsam kurze Erklärvideos zu Legehandlungen und Bündelungsaktivitäten an der Stellenwerttafel und begleiten diese sprachlich (z. B. mit der Unterstützung eines Wortspeichers).
Inhaltlich würde sich z. B. zunächst das Legen und anschließende Bündeln im Aufgabenformat „Vorgabe von unkonventioneller Zahldarstellungen“ oder auch das „Systematische Verändern der vorgegebenen anschaulichen Zahldarstellung“ anbieten. Alternativ wären auch kurze Videos zu verschiedenen Leitfragen, die vielfältige sprachliche Aktivitäten ermöglichen, wie „Wie kann ich Zahlen mit Material darstellen?“ oder „Wie kann ich geschickt entbündeln, wenn ich von 103 einen Zehner wegnehmen möchte?“ möglich. Dazu könnte ein möglicher Arbeitsaufträge sein: „Legt eine Zahl (z. B. eine große oder kleine Zahl, eine bestimmte oder eine beliebige Zahl) mit Material in die Stellenwerttafel. Wie geht ihr vor? Erklärt und filmt ein Erklärvideo für ein Kind, dass die Aufgabe noch nicht kennt.“
Bei der Aufnahme der Erklärvideos kann ein Kind auf dem Tisch die Legehandlungen mit konkretem Material durchführen. Das andere Kind filmt mit dem Tablet die Legehandlungen von oben und erklärt die Vorgehensweisen (mit Unterstützung des Partners bzw. der Partnerin). Bei der Planung und Aufnahme der Videos können sich die Kinder nochmals über die Verbalisierung der Zahldarstellungen und Legehandlungen bewusstwerden und diese durch das nachträgliche Anschauen oder das Präsentieren des Videos vor anderen Kindern reflektieren.
Mögliche Reflexionsfragen für das gemeinsame Betrachten der Videos in Kleingruppen oder der Klasse wären: Habt ihr die Erklärung verstanden? Würde ein Kind aus einer anderen Klasse die Erklärung auch verstehen? Welche Begriffe aus dem Wortspeicher hätten unsere Erklärung noch verständlicher gemacht? Was könnten wir bei der Erstellung eines neuen Erklärvideos noch besser machen? Was hat euch gut gefallen?
Die Erstellung der Erklärvideos durch die Kinder verfolgt nicht das Ziel, dass „ideale“ Videos entstehen, sondern dass sich die Kinder im Vorhinein Gedanken um die sprachliche Begleitung der Handlungen machen und diese im Nachgang durch ein erneutes Anschauen reflektieren können.
Möglichkeiten individueller Unterstützung
Legen von Zahldarstellungen
Insbesondere bei Kindern mit Wahrnehmungsschwierigkeiten bietet sich eine in Abschnitte geteilte Sortierunterlage am. Hierdurch kann das geordnete Legen der Materialien unterstützt werden.
Abbildung 32
Möglichkeiten individueller Unterstützung
Ordnen des Materials
Sind auf der Sortierunterlage zusätzlich beispielsweise Abbildungen der Hunderterplatte, der Zehnerstangen oder der Einerwürfel vorhanden, bietet die Sortierunterlage auch eine inhaltliche Unterstützung beim Sortieren und Ordnen des Legematerials nach Stellenwerten.
Abbildung 33
Auch durch den Einsatz einer farbigen Sortierunterlage kann das Sortieren und Ordnen des Legematerials unterstützt werden. In der Montessori-Pädagogik werden die Farben grün, rot und blau zur Repräsentation der Stellenwerte bei der Zahldarstellung genutzt.
Abbildung 34
Wichtig:
Zu einem späteren Zeitpunkt muss die Ablösung von einer farbigen Unterscheidung der Stellenwerte erfolgen. Geschieht dies nicht, besteht die Gefahr, dass die Zuordnung zu Stellen bzw. die Anordnung der Stellenwerte einzig auf der Grundlage einer (gelernten und auswendig gewussten) Farbfolge erfolgt.
Möglichkeiten individueller Unterstützung
Dokumentation der Zahldarstellungen
Zur Dokumentation von Zahldarstellungen können Kinder Stempel nutzen. Diese können aus Moosgummi selbst hergestellt werden. Damit auch der Strich für den Zehner und der Punkt für den Einer gut sichtbar sind und die Stempel für die Kinder handhabbar, dürfen diese nicht zu klein sein. Zudem sollte auf die Größenverhältnisse der Hunderter, Zehner und Einer geachtet werden. Auch eine Dokumentation der Zahldarstellungen am Computer ist möglich.
Möglichkeiten individueller Unterstützung
Verbalisierung der Zahldarstellungen
Um die Zahldarstellungen versprachlichen zu können, müssen die Kinder über zentrale Begriffe und Redemittel verfügen. Gemeinsam mit den Kindern können Sprachmuster festgelegt und zentrale Begriffe erarbeitet werden (Anlegen eines Wortspeichers).
Grundlegende Begriffe und Sprachmuster:
Hunderter, Zehner, Einer, Hunderterplatte, Zehnerstange, Einerwürfel, Stellen(-wert),
Lege _ Hunderter, _Zehner und _Einer, ein Zehner (Hunderter, Einer) weniger, ein Zehner (Hunderter, Einer) mehr, Auf der Karte sind _Hundertertafeln, _Zehnerstangen, _Einerwürfel abgebildet, ....
Eine Unterstützung kann es sein, wenn den Kindern konkrete Satzbausteine angeboten werden (z.B. auf einer Karteikarte).
