Bedeutung und Besonderheiten des Zahlenrechnens
Bedeutung
Den Aufgaben und Zielsetzungen des Lehrplans für die Grundschule gerecht wird der Mathematikunterricht dann, wenn das Lernen von Mathematik „durchgängig als konstruktiver, entdeckender Prozess verstanden wird“ (MSW NRW 2008, S. 55).
Gegenüber den schriftlichen Rechenverfahren, bei denen es eher um das Abarbeiten einer festgelegten Abfolge von Schritten geht, liegen die Vorteile des Zahlenrechnens in der impliziten Anforderung, Zahlbeziehungen und Rechengesetze geschickt zu nutzen, eigene Darstellungen für Rechenwege zu finden und über Zahlen, Zahlbeziehungen und – zusammenhänge sowie verschiedene Rechenwege und Vorgehensweisen nachzudenken und zu sprechen.
Ein solch verstehens- und kommunikationsorientiertes Arbeiten ist wichtig für alle Schülerinnen und Schüler. Aber insbesondere Kinder mit Lernschwierigkeiten profitieren von einem Unterricht, der Verständnis und Einsicht in den Mittelpunkt stellt, denn „nachhaltiges Lernen muss sich gerade für die schwächeren Lernenden konsequent am Aufbau von Verständnis orientieren [...]“ (Prediger et al. 2014, S. 7).
Besonderheiten
Charakteristisch für das Rechnen mit Zahlen ist das Operieren mit Zahlganzheiten: Schwierige und komplexe Aufgaben werden in leichtere Teilaufgaben zerlegt und unter Verwendung von Zahlbeziehungen, Rechengesetzen und Rechenvorteilen gelöst.
Dabei sollten die Schülerinnen und Schüler zunächst eigene Rechenwege entwickeln.
Für den Mathematikunterricht bedeutet das, dass den Kindern ausreichend Zeit eingeräumt werden muss, um selbständig zu überlegen, wie eine Aufgabe – auf der Grundlage von Zahlbeziehungen und Rechengesetzen – gelöst werden kann.
Damit eigene Ideen umgesetzt und Vorgehensweisen bzw. mögliche Rechenwege geplant, entwickelt und dargestellt werden können, ist hier der Einsatz von Materialien und Darstellungsmitteln fundamental.
Weitere Informationen hierzu sowie ausführliche Hinweise zur Arbeit im Unterricht finden Sie im zweiten Modul des Hintergrundes: Rechenwege.
Analysiert man mögliche Vorgehensweisen und Rechenwege, dann können verschiedene, den Rechenwegen zu Grunde liegende Strategien unterschieden werden.
In Bezug auf die Subtraktion lassen sich die folgenden Hauptstrategien voneinander abgrenzen (in Anlehnung an Wittmann & Müller 1993, S. 87; Selter 2000, S. 231):
Hauptstrategien des Zahlenrechnens (Subtraktion):
Aufgabe: 496 — 198
Schrittweise (Der Subtrahend wird zerlegt)
Lea
Lea subtrahiert in einem ersten Schritt direkt 190. Von dem Ergebnis 306 muss sie nun noch 8 abziehen. Sie zerlegt die 8 in 6 und 2 und zieht beide Zahlen nacheinander ab.
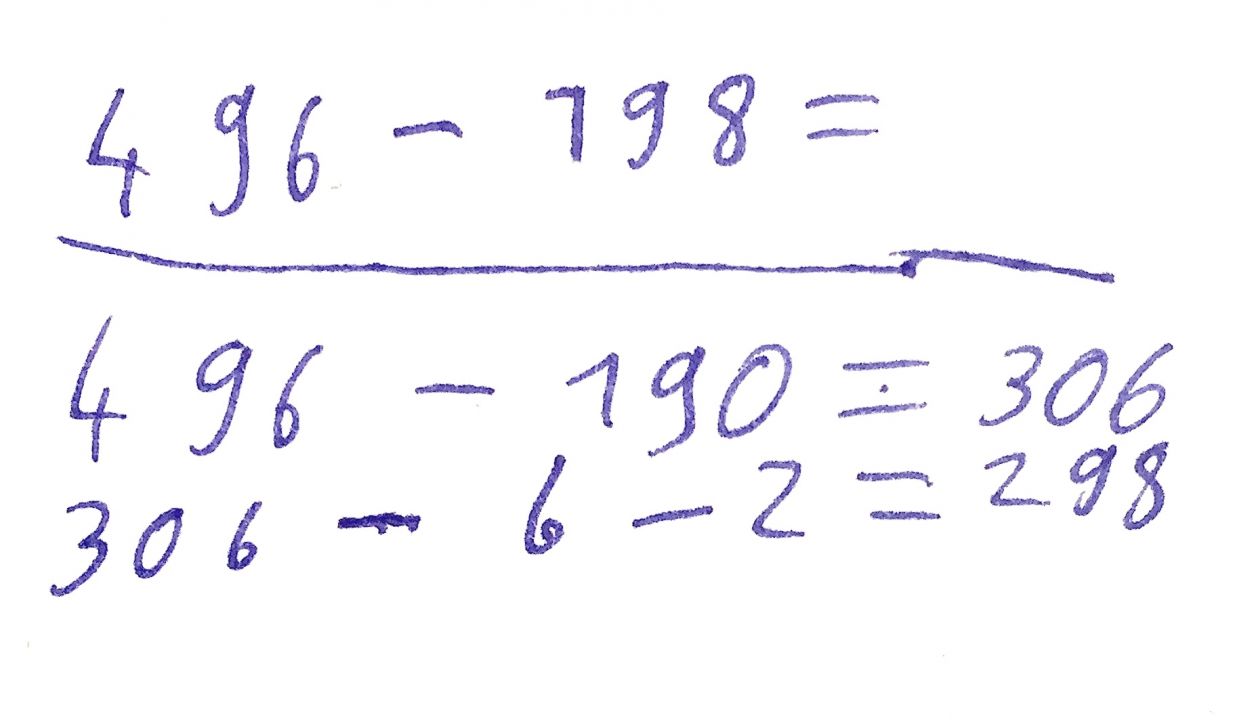 Abb. 1
Abb. 1
Stellenwerte extra
Rico
Rico rechnet zuerst 400 minus 100. Dann rechnet er 90 minus 90 und anschließend notiert er 6 — 8. D.h. er muss nun einen Hunderter (Zehner) anbrechen.
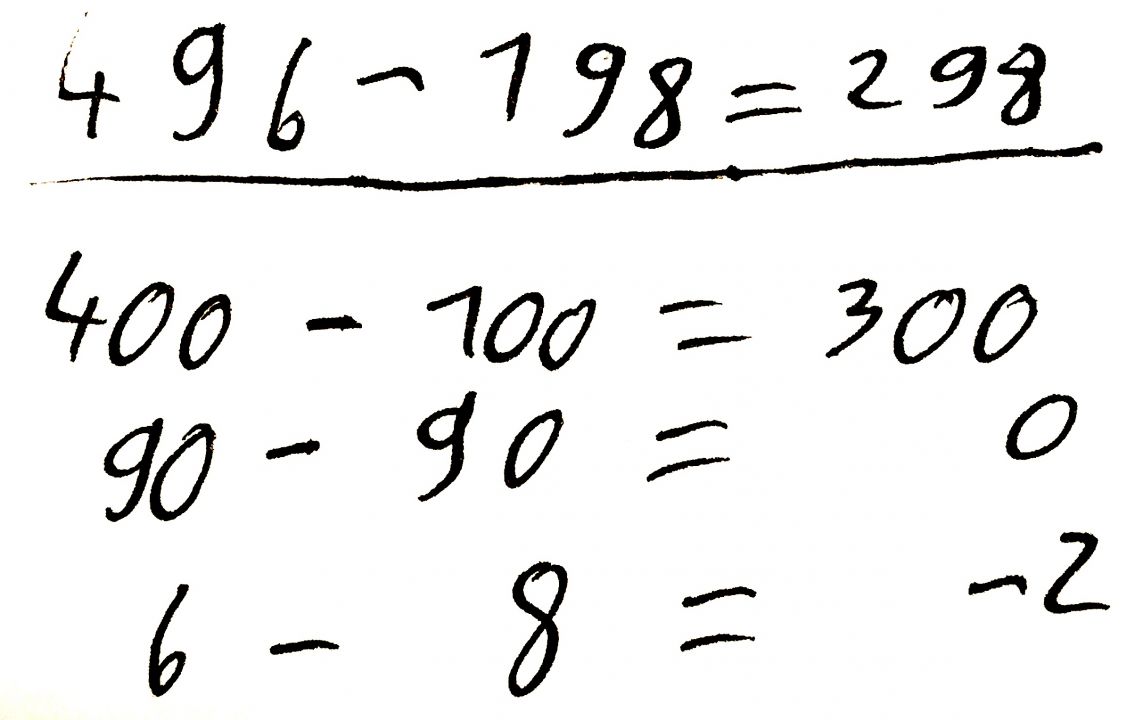 Abb. 2
Abb. 2
Hilfsaufgabe
Yusuf
Yusuf rechnet am Rechenstrich zunächst eine einfachere Aufgabe. Statt 198 zieht er 200 ab. Das ergibt 296. Dann zeichnet er einen zweiten Bogen, an den er „+2“ schreibt und erhält 298. D.h. er addiert zu 296 noch 2 hinzu, da er zu Beginn 2 zuviel abgezogen hatte (200 statt 198).
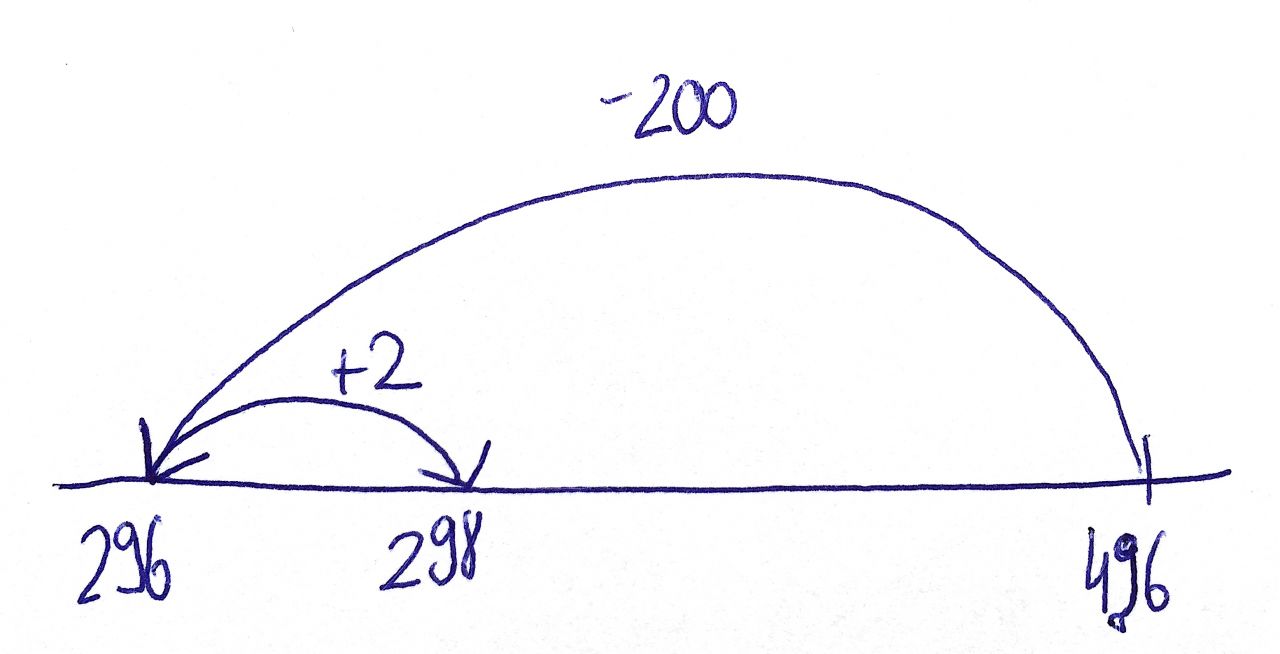 Abb. 3
Abb. 3
Vereinfachen (Konstanz der Differenz)
Marla
Marla vergrößert den Minuenden und den Subtrahenden um die gleiche Zahl. Die Differenz ändert sich nicht.
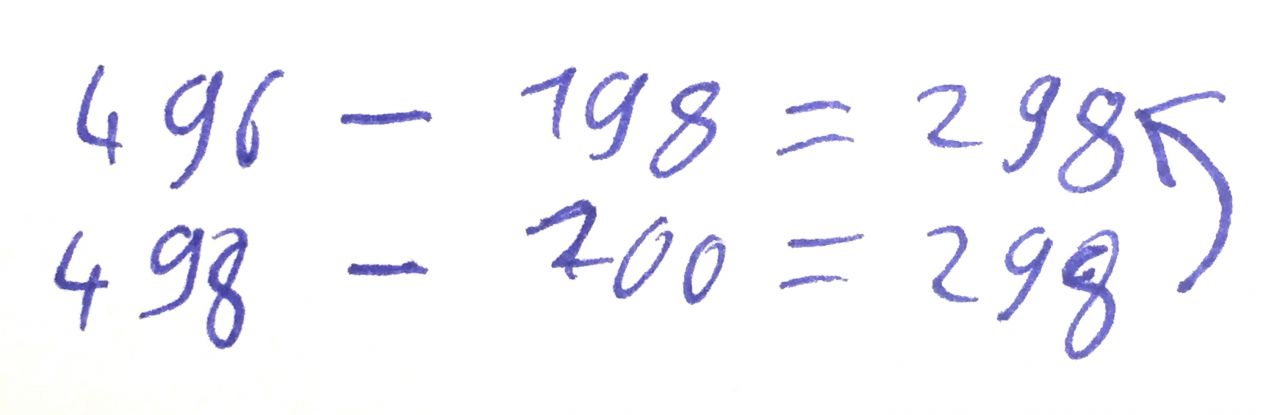 Abb. 4
Abb. 4
Ergänzen
Tami
Tami weiß, dass sie Differenzen auch durch Ergänzen ermitteln kann. Ausgehend vom Subtrahenden 198 ergänzt sie am Rechenstrich zunächst 2 und dann noch 296. Insgesamt ergänzt sie somit 298.
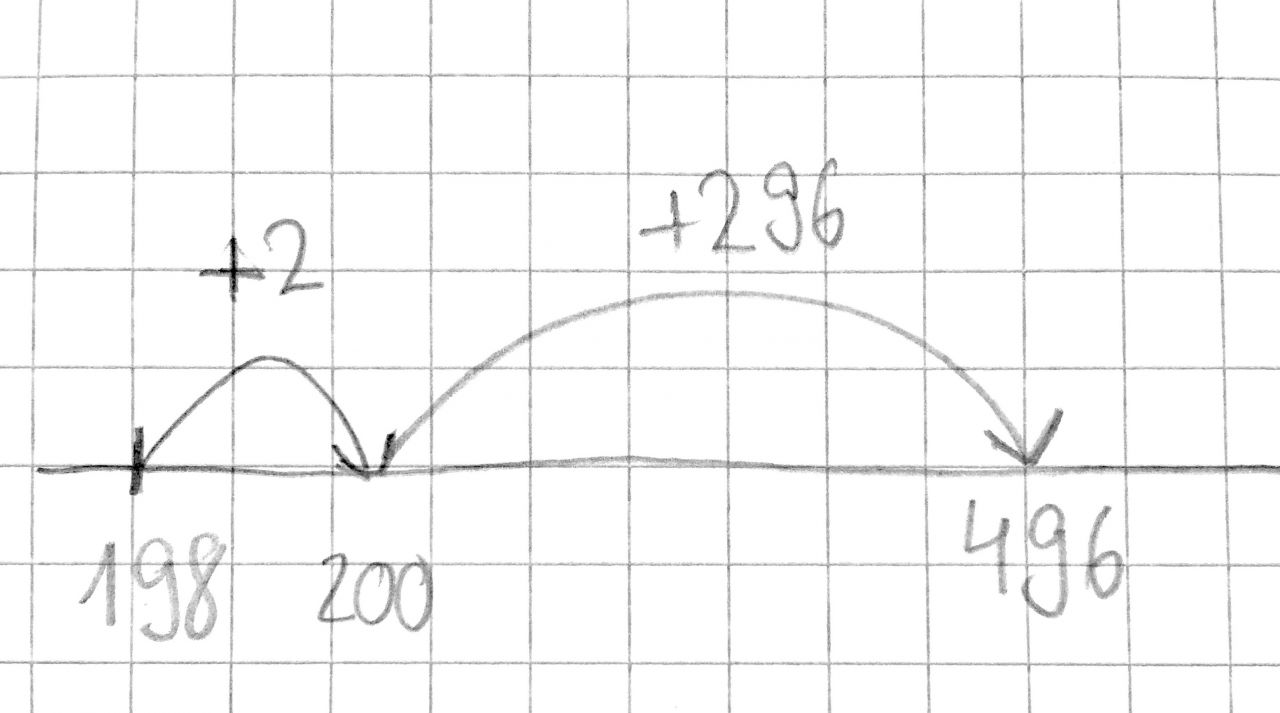 Abb. 5
Abb. 5
Da – unabhängig von der Rechenoperation – beim halbschriftlichen Rechnen keine konkreten Vorgehensweisen festgelegt sind, lassen sich nicht alle Rechenwege, die Kinder im Unterricht zeigen, hier problemlos einordnen – immer wieder gibt es Mischformen oder auch individuelle z. T. sehr komplexe Vorgehensweisen (vgl. hierzu auch KIRA: halbschriftliche Subtraktion).
Mischform (Stellenwerte extra und Schrittweise)
Sibel
Sibel schaut zunächst auf die Hunderter und rechnet 400 minus 100. Anschließend rechnet sie noch 396 minus 98 schrittweise. Als Ergebnis erhält sie 298.
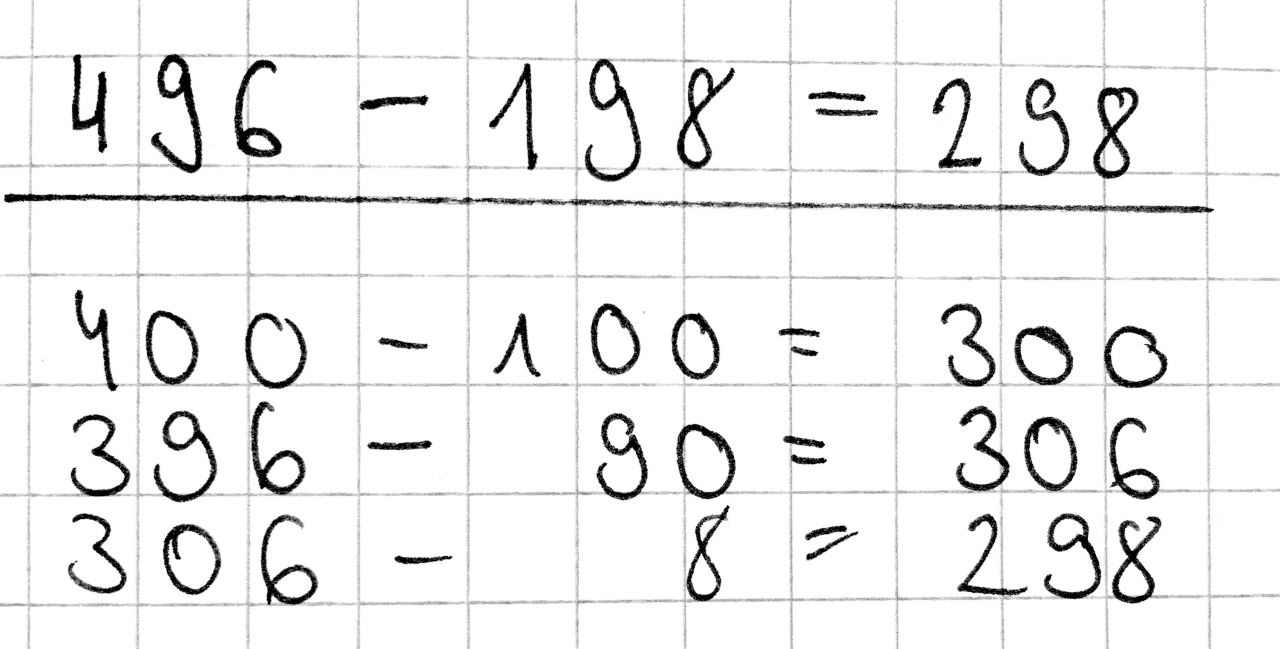 Abb. 6
Abb. 6
Auch die Art der Darstellung eines Rechenweges (am Rechenstrich, als Zeichnung, symbolisch, mit Material, ...) ist beim Zahlenrechnen nicht vorgegeben.
Darüber hinaus sollten die Kinder – beispielsweise bei der symbolischen Notation eines Rechenweges - selbständig bestimmen dürfen, ob überhaupt und welche Teilschritte ihrer Rechnung sie notieren, denn diese stellen lediglich eine Merkhilfe dar.
Eine Strategie – verschiedene Darstellungen
Strategie "Schrittweise" / Aufgabe 64 — 39
 Abb. 7
Abb. 7
Rike
Rike nutzt das Dienes–Material und nimmt zunächst 3 Zehner weg. Um dann noch 9 Einer wegnehmen zu können, muss sie einen Zehner in 10 Einer umtauschen.
 Abb. 8
Abb. 8
Calvin
Calvin zeichnet die Zahl 64. Zuerst deckt er 3 Zehner ab, anschließend 4 Einer. Calvin weiß, dass 1 Zehner aus 10 Einern besteht. Er deckt noch 5 Einer ab (Teil des Zehners).
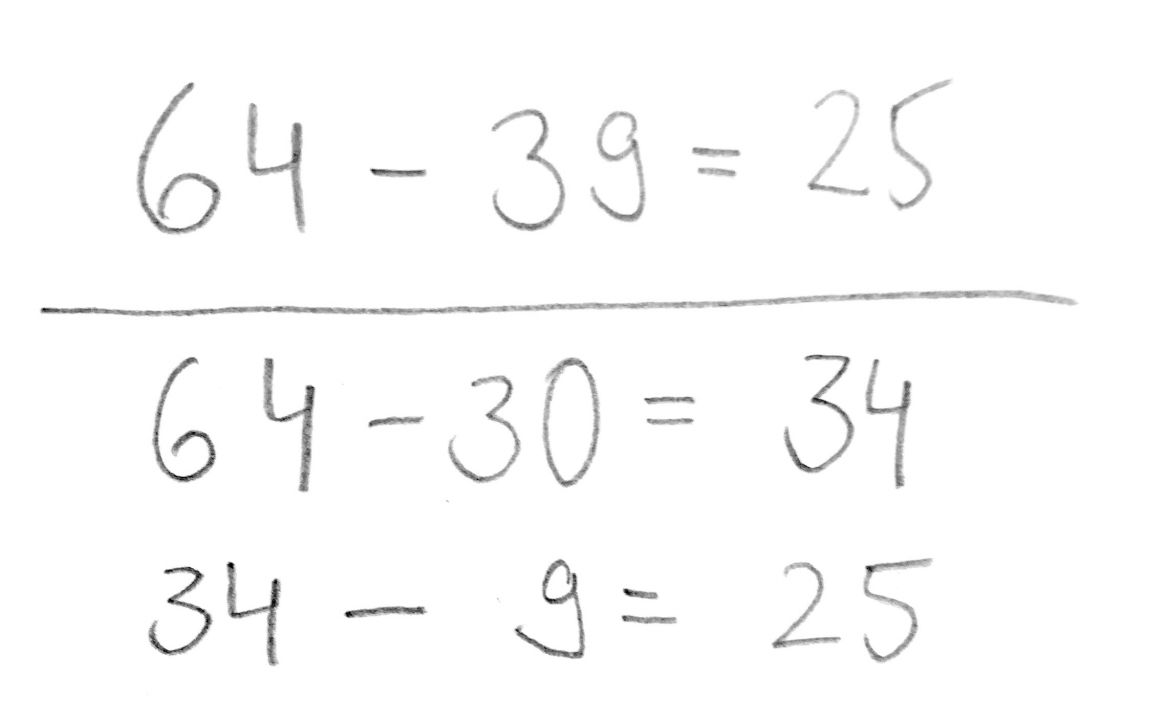 Abb. 9
Abb. 9
Sara
Sara verwendet mathematische Symbole, um ihre Rechnung zu notieren. Sie schreibt ihre Teilrechnungen untereinander.
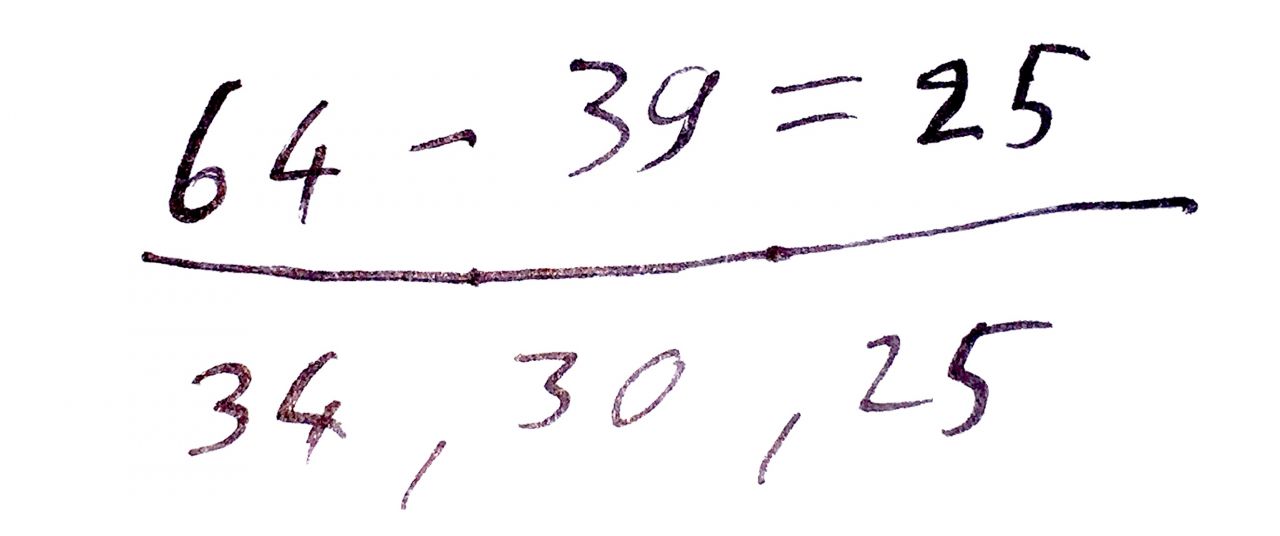 Abb. 10
Abb. 10
Tobias
Tobia nutzt – wie Sara – mathematische Symbole, um seine Rechnung zu notieren. Er notiert allerdings ausschließlich die Ergebnisse seiner Teilrechnungen.
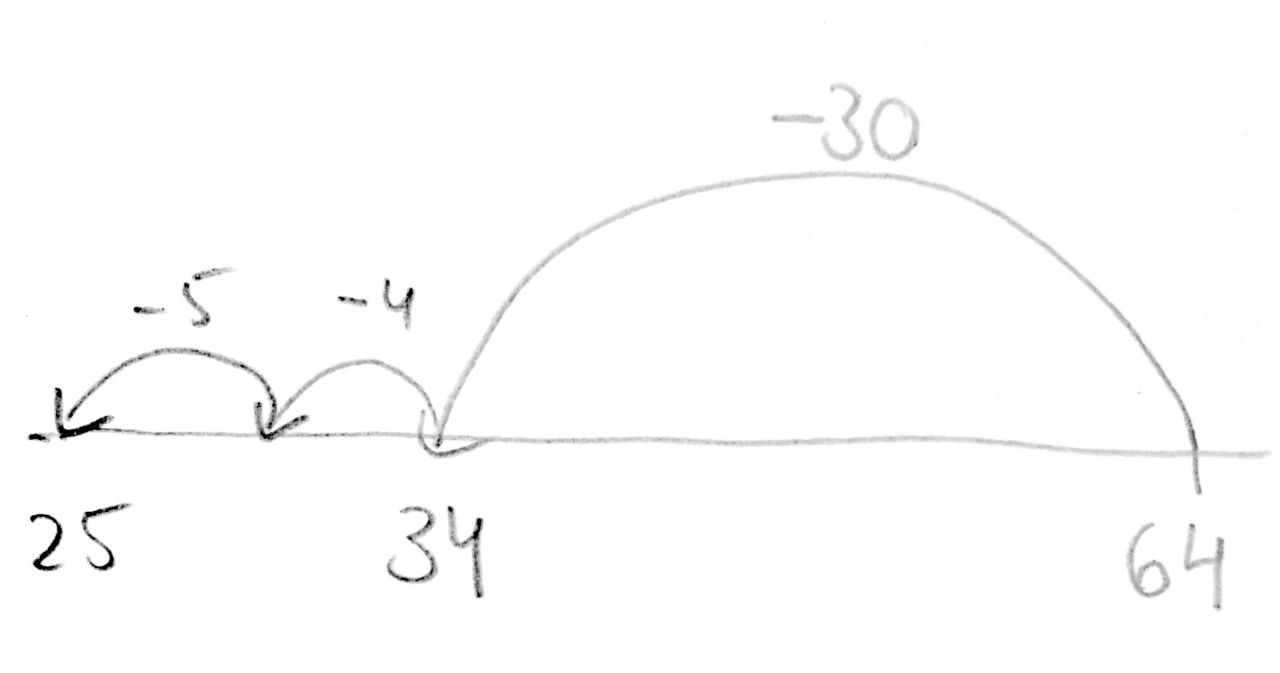 Abb. 11
Abb. 11
Lutz
Lutz nutzt den Rechenstrich, um die Aufgabe in Teilschritte zu zerlegen. Wie Sara verwendet er mathematische Symbole.
 Abb. 12
Abb. 12
Rico
Rico verbalisiert seine Vorgehensweise (sprachliche Symbole).