Auf dieser Seite wird exemplarisch illustriert, wie gemeinsame Unterrichtsphasen umgesetzt werden können, in denen möglichst alle Lernende aktiviert werden. Die genutzten Materialien zur Basisaufgabe, der Reduktion, Erweiterung und Möglichkeiten individueller Unterstützung sind der Aufgabenstellung „Subtraktion am Rechenstrich“ entnommen und leicht angepasst. Somit lautet der Arbeitsauftrag für die Lernenden:
 Abbildung 1: Arbeitsauftrag in der Arbeitsphase
Abbildung 1: Arbeitsauftrag in der Arbeitsphase
Die auf dieser Seite dargestellten Videos und dazu passenden Materialien stellen eine mögliche erste Unterrichtseinheit einer Unterrichtsreihe dar. Das Ziel dieser Unterrichtseinheit besteht darin, dass die Kinder verschiedene Rechenwege der Subtraktion im Zahlraum bis 1000 ordnen, indem sie diese nachvollziehen, beschreiben sowie Gemeinsamkeiten und Unterschiede benennen. Dabei liegt der Fokus auf den halbschriftlichen Strategien „Schrittweise“ und „Hilfsaufgabe“.
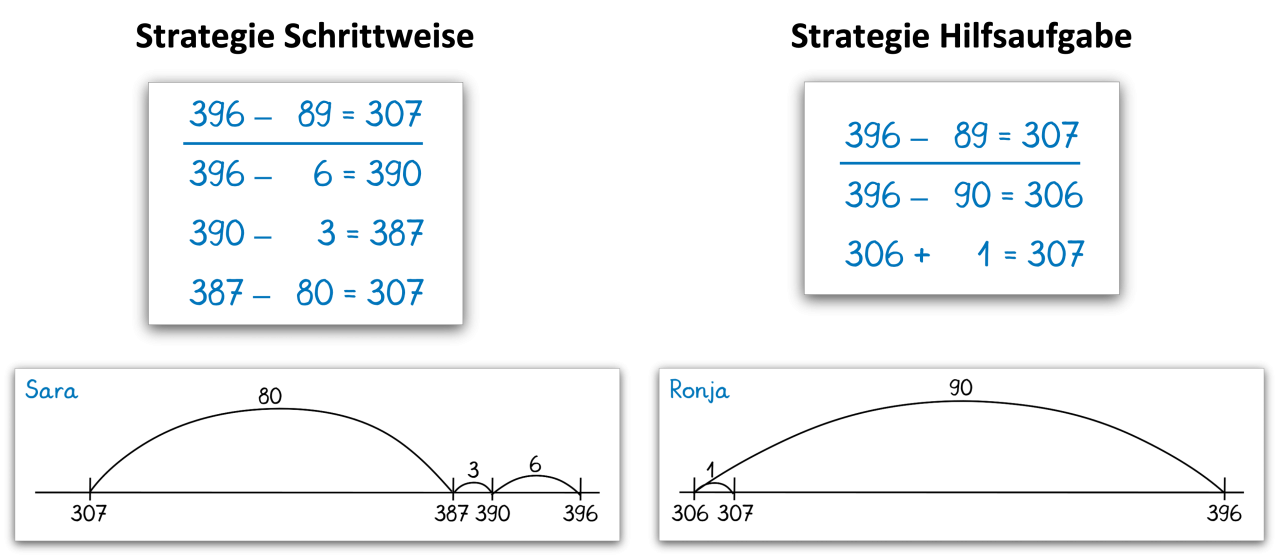 Abbildung 2: Strategien
Abbildung 2: Strategien
Weiterführende Informationen zu den Strategien finden Sie hier:
https://mahiko.dzlm.de/node/70
Im Folgenden finden Sie Videos, in denen eine Lehrkraft exemplarisch berichtet, wie sie die Aufgabenstellung in einer heterogenen, inklusiven Lerngruppe aus einem dritten Schuljahr in den folgenden Unterrichtsphasen umgesetzt hat
Außerdem berichtet sie von Differenzierungsmaßnahmen, die aus Aufgaben der Reduktion und Erweiterung sowie den individuellen Unterstützungsmaßnahmen bestehen.
Zu jedem Video finden Sie jeweils darunter die im Video genutzten und weiterführende Materialien, so dass diese direkt im eigenen Unterricht genutzt werden können. Für die Einstiegs- und Reflexionsphase werden außerdem jeweils mögliche Elemente beschrieben, die sich für die Aktivierung möglichst aller Lernenden eignen können.
Video zur Umsetzung der Einstiegsphase
Die folgende Übersicht zeigt die im Video dargestellten Inhalte. Ein Klick auf das Pluszeichen führt jeweils zu dem dargestellten Material:
Gespeichert von anna.koester_30508 am Mi, 02/12/2025 - 14:47
Abbildung 3: Material Einstiegsphase
Möglichkeiten zur Aktivierung aller Lernenden in der Einstiegsphase
Die Einstiegsphase hat die Funktion zu motivieren, zu aktivieren, sich mit dem Unterrichtsgegenstand auseinanderzusetzen und die Unterrichtseinheit zu strukturieren. Dabei ist es wichtig, möglichst alle Lernenden einzubinden. Hierzu werden die im Video genutzten Elemente für die vorliegende Unterrichtseinheit exemplarisch dargestellt und erläutert (vgl. Richter, 2011; Sander & Pohl, 2022).
Gezielt Aufgaben auswählen, um unterschiedliche Zugänge zu ermöglichen
Es bietet sich an, Aufgaben so auszuwählen, dass alle Lernenden mitdenken und verschiedene Kinder sich an unterschiedlichen Stellen aktiv einbringen können. Möglichkeiten sind dabei (vgl. Häsel-Weide & Nührenbörger, 2021; PIKAS, 2013):
-
Berücksichtigung des Zahlraums (hier: Zahlraum 100, in dem alle Kinder sicher sind)
-
Berücksichtigung von bekannten Strategien (hier: Strategie Schrittweise, die bereits im vorherigen Schuljahr erarbeitet wurde)
-
Auswahl einer Aufgabe aus der Reduktion (hier: Rechenstriche im reduzierten Zahlraum und Fokus auf einen einzelnen Rechenschritt).
Ein zentraler Aspekt ist es also, vorausgehende Unterrichtsstunden bzw. -reihen zu berücksichtigen und auch daran zu erinnern (hier: an das schrittweise Rechnen bei der Addition aus dem vorherigen Schuljahr erinnern).
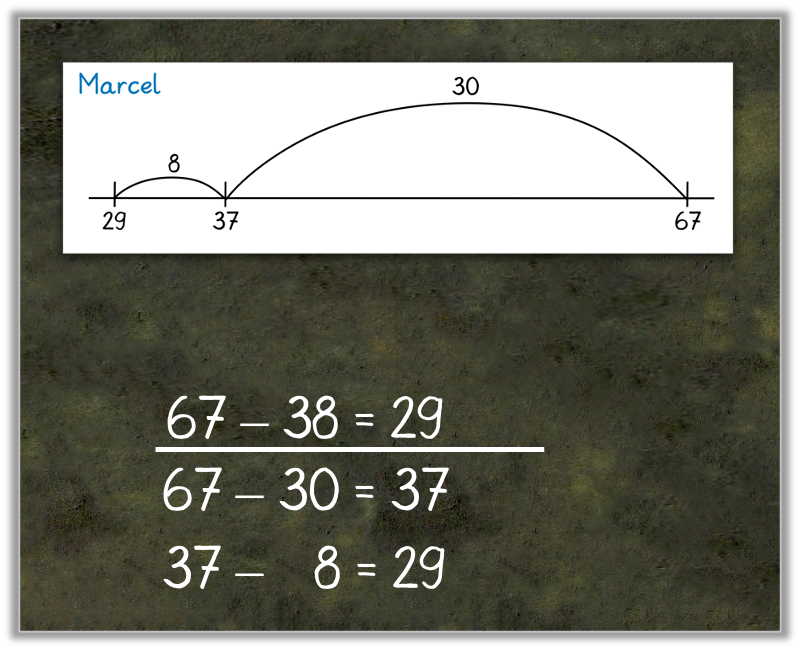 Abbildung 4: Aufgaben im Reduzierten Zahlraum
Abbildung 4: Aufgaben im Reduzierten Zahlraum
Durch Impulse zum Mitdenken, Fokussieren und Hinterfragen aktivieren
Um möglichst viele Lernende zu aktivieren, dem Unterrichtsgespräch zu folgen, bietet es sich an, ein vielfältiges Repertoire an Fragen bereit zu halten und Fragen zu stellen, die die Lernenden zum Mit- und Weiterdenken auffordern, beispielsweise durch die Aufforderung
-
zum Nachvollziehen (z. B. „Was ist der nächste Schritt? Warum müssen wir jetzt noch 8 abziehen?“).
-
zur Darstellungsvernetzung (z. B. „Wo siehst du diesen Rechenschritt am Rechenstrich?“ oder „Wie erkennst du das Ergebnis?“)
-
zum Beschreiben (z. B. „Was hat Anton gemacht?“)
-
zum Begründen (z. B. „Warum ist das der erste Rechenschritt?“)
Geeignete Darstellungsformen lernwirksam nutzen (lassen)
Um die Kinder dabei zu unterstützen, die Inhalte nachzuvollziehen und Verständnis aufzubauen, ist die Nutzung von geeigneten Darstellungsformen zentral:
-
Damit Kinder das Vorgehen nachvollziehen können, sollte man als Lehrkraft selbst bildliche Darstellungen, konkrete Materialien sowie Gesten nutzen.
-
Auch die Kinder sollten aufgefordert werden, mathematische Symbole, Sprache, Handlungen und Bilder zu vernetzen (hier: Rechenstrich, Notation der Aufgabe und Beschreibung der Aufgabe).
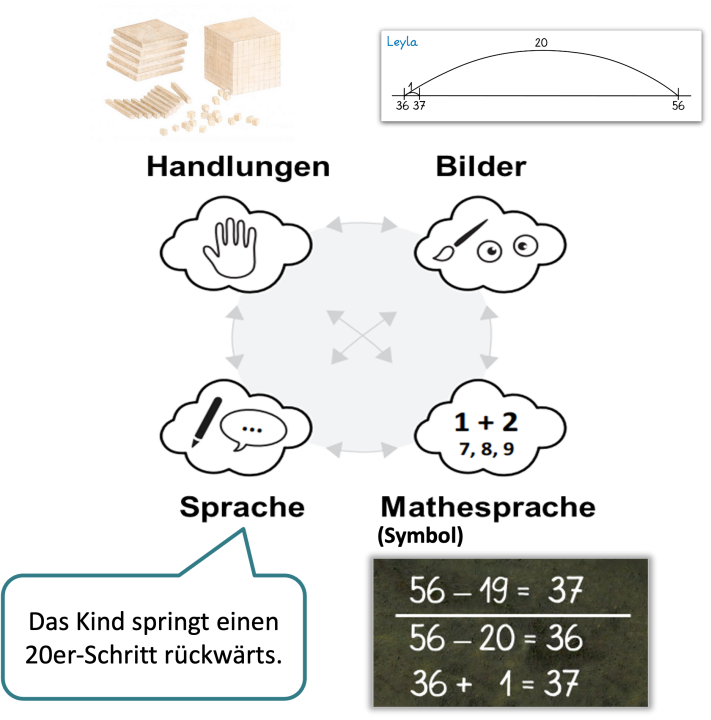 Abbildung 5: Darstellungsvernetzung (Abbildung in Anlehnung an PIKAS, 2020, S. 20)
Abbildung 5: Darstellungsvernetzung (Abbildung in Anlehnung an PIKAS, 2020, S. 20)
Geeignete Partizipationsmöglichkeiten für individuelle Voraussetzungen finden
Kinder bringen viele unterschiedliche Vorerfahrungen, Bedürfnisse und Interessen mit. Diese sind in jeder Klasse sehr individuell. Je besser man diese kennt, desto besser, können sie berücksichtigt werden. Es bietet sich an, bereits in der Planung mögliche Partizipationsmöglichkeiten zu berücksichtigen und dabei zu überlegen, welche Kinder an welchen Stellen wie eingebunden und unterstützt werden können (z. B. beim Notieren einzelner Rechenschritte, das Nutzen einer Fokussierung, das Anbringen von Wortkarten, gezielte Impulsfragen …) (vgl. PIKAS, 2013).
Weiterführende Informationen zu „Diagnosegeleitet fördern“ finden Sie hier:
https://pikas-mi.dzlm.de/node/54
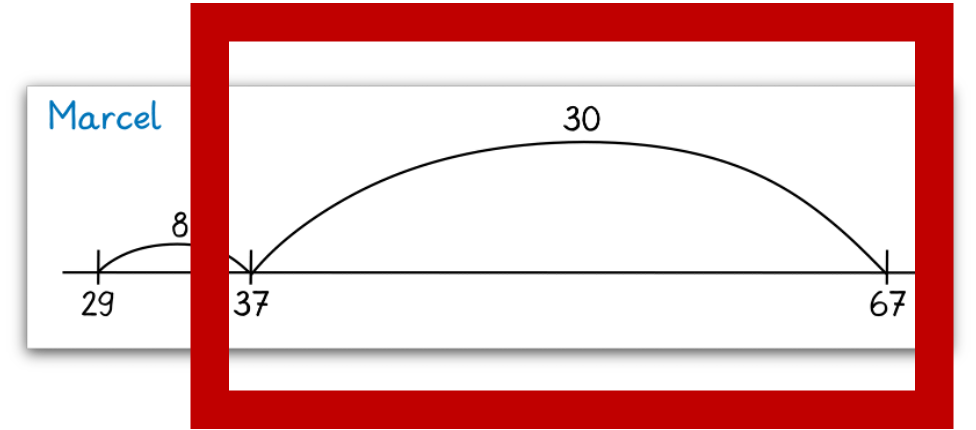 Abbildung 6: Fokussierung auf einzelne Schritte (Rahmen)
Abbildung 6: Fokussierung auf einzelne Schritte (Rahmen)
Zum Probehandeln auffordern
Um sicherzustellen, dass die Lernenden das Vorgehen für die Arbeitsphase verstehen, ist es zentral:
-
das Vorgehen selbst explizit zu machen oder
-
die Kinder das erarbeitete Vorgehen auf ein weiteres Beispiel übertragen zu lassen (z. B. andere Zahlwerte, andere Strategie, anderer Zahlraum, ...).
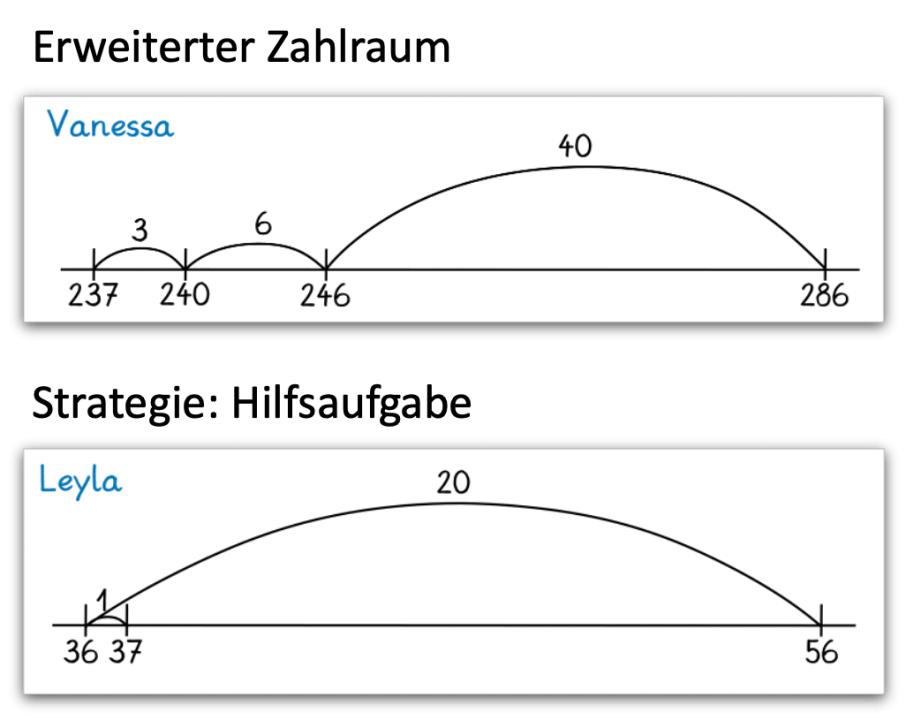 Abbildung 7: Probehandeln
Abbildung 7: Probehandeln
Wie eine mögliche Arbeitsphase zu der Aufgabenstellung gestaltet und organisiert sein kann und was mögliche Arbeitsergebnisse der Kinder sein können, zeigt das folgende Video.
Video zur Umsetzung der Arbeitsphase
Die folgende Übersicht zeigt die im Video dargestellten Inhalte. Ein Klick auf das Pluszeichen führt jeweils zu dem dargestellten Material:
Gespeichert von anna.koester_30508 am Mi, 02/12/2025 - 14:52
Abbildung 8: Material Arbeitsphase
Video zur Umsetzung der Reflexionsphase
Die folgende Übersicht zeigt die im Video dargestellten Inhalte. Ein Klick auf das Pluszeichen führt jeweils zu dem dargestellten Material:
Gespeichert von anna.koester_30508 am Mi, 02/12/2025 - 14:55
Abbildung 9: Material Reflexionsphase
Möglichkeiten zur Aktivierung Aller Lernenden in der Reflexionsphase
In der Reflexionsphase soll der Erkenntnisgewinn der Unterrichtseinheit gesichert, vertieft und transferiert werden. Dies geschieht beispielsweise durch:
-
die Präsentation und Betrachtung der Ergebnisse
-
das Einfordern von Begründungen von Lösungen
-
das Erklären von Mustern
-
die bewusste Auseinandersetzung mit Ergebnissen von anderen.
So sollen Anknüpfungspunkte für weitere Lernprozesse geschaffen werden (vgl. Richter, 2011; Sander & Pohl, 2022).
In der dargestellten, exemplarischen Unterrichtseinheit wurden verschiedene Elemente eingesetzt, um möglichst viele Lernende einzubinden.
Arbeitsergebnisse präsentieren lassen und Beobachtungsauftrag stellen
Kinder sollen durch die Präsentation ihrer eigenen Überlegungen und Einsichten, das eigene Verständnis vertiefen. Dabei gibt es unterschiedliche Umsetzungsmöglichkeiten: Alleine, gemeinsam mit dem Tandemkind aus der Arbeitsphase oder als Gruppe der Mathekonferenz.
Damit möglichst viele Kinder aktiv bleiben, können Aufträge an die zuhörenden Kinder gegeben werden, zum Beispiel:
-
die vorgestellten Ergebnisse mit den eigenen zu vergleichen und ggf. zu ergänzen (Beobachtungsauftrag: „Es stellen gleich verschiedene Tandems vor, wie sie ihre Rechenstriche geordnet haben. Ihr sollt mitdenken: Welche Rechenstriche passen noch dazu? Warum?")
-
Ergebnisse zu antizipieren („Erkennt ihr eine Strategie?“ oder „Was hat sich das Tandem / die Gruppe wohl überlegt?“).
(vgl. Schwier 2010; PIKAS, 2013)
Beziehungen zwischen Arbeitsergebnissen herstellen
Ein zentraler Aspekt der Reflexionsphase ist es, dass Beziehungen zwischen den unterschiedlichen Arbeitsergebnissen hergestellt werden. Eine Tätigkeit, die es der Lerngruppe eine aktive Auseinandersetzung mit den Arbeitsergebnissen ermöglicht, ist das gemeinsame Ordnen. Entscheidend dabei ist es, sich immer wieder Begriffe und Vorstellungen auszuhandeln. Dabei sind zwei Punkte zentral:
-
Sich darüber zu verständigen, wie etwas heißt und was es bedeutet. Beispielsweise wird hier ausgehandelt, dass diese Rechenwege zusammenpassen, weil bei allen der Subtrahend in Schritte aufgeteilt wird und es wird sich auf einen geeigneten Namen („In Schritten zurück") geeinigt (siehe Abbildung 9).
-
Sich auf richtige Lösungen und geschickte Lösungswege verständigen. Damit Lernende, sinnvolle und hilfreiche Verfahren herausfiltern können, geht es auch darum, diese im Laufe des Unterrichts zu erarbeiten und zu benennen.
(vgl. Götze & Meyer, 2010; Häsel-Weide, 2014; Schütte, 2002)
Mehr Informationen zur Moderation von solchen Plenumsphasen lassen sich hier finden:
https://pikas-mi.dzlm.de/node/615
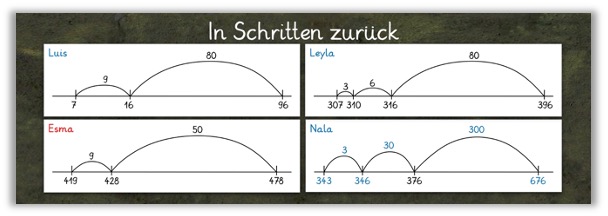 Abbildung 10: Beziehung zwischen Arbeitsergebnissen
Abbildung 10: Beziehung zwischen Arbeitsergebnissen
Durch Impulse zum Mitdenken, Fokussieren und Hinterfragen aktivieren
Auch in der Reflexionsphase sollten möglichst viele Kinder durch Impulse aktiviert werden. Zentral dabei ist es, auf Suggestiv- oder Ja/Nein-Fragen zu verzichten und stattdessen authentische und offene Fragen zu stellen (z. B. „Wie habt ihr sortiert? Welche Rechenwege passen zusammen? Welche Rechenwege passen noch dazu? Warum passt dieser Rechenweg nicht dazu?“).
Mehr zu geeigneten Fragen in Plenumsphasen lässt sich hier finden: https://pikas-mi.dzlm.de/node/616
Geeignete Darstellungsformen lernwirksam nutzen (lassen)
Erkenntnisse und Entdeckungen sollten für möglichst viele Lernende explizit gemacht werden durch
-
die Vernetzung von mathematischen Symbolen, Sprache, Bilder und Handlungen
-
die Nutzung eines Sprachspeichers (siehe Abbildung 10)
-
die Nutzung von Gesten
-
die Nutzung von Forschermitteln.
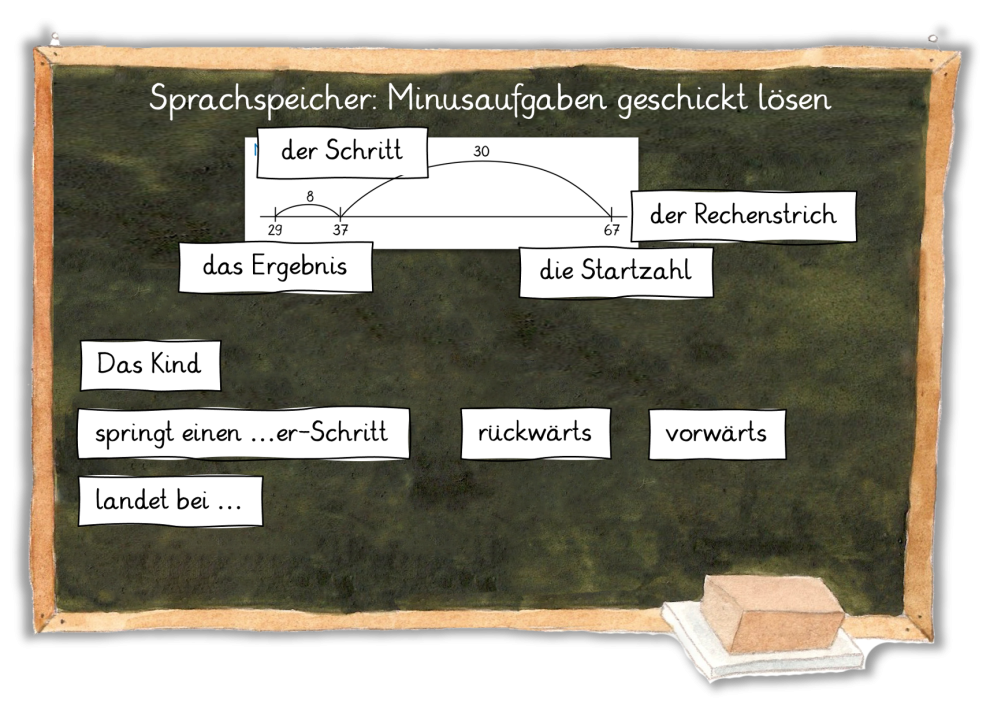 Abbildung 11: Sprachspeicher
Abbildung 11: Sprachspeicher
Geeignete Partizipationsmöglichkeiten für individuelle Voraussetzungen finden
Um möglichst viele Kinder mit einzubinden, ist es zentral, unterschiedliche Arbeitsergebnisse zu verschiedenen Aufgaben vorstellen zu lassen. Es bietet sich hier zum Beispiel an, mit den Ergebnissen aus der Reduktion zu starten.
Auch in der Reflexionsphase können einzelne Kinder gezielt eingebunden werden, z. B. durch Aufforderung
-
zur Wiederholung von bestimmten zentralen Aspekten („Welche Gemeinsamkeiten hat Malik entdeckt?“ oder „Warum gehören die beiden Rechenstriche beide zu der Strategie Hilfsaufgabe?“)
-
zur Nutzung des Sprachspeichers („Beschreibe deine Entdeckung mit den Satzbausteinen.“ oder „Wie haben wir das im Sprachspeicher genannt?“)
-
zum Fortsetzen einer Strategie („Sortiere weiter.“ oder „Wie geht es weiter?“)
-
Denkprozesse bzw. Strukturen mit konkret handelnden Darstellungen zu veranschaulichen („Lege die Aufgabe mit Zehnerstreifen und Plättchen.“).
(vgl. PIKAS, 2013)
 Abbildung 12: Reduktion und Erweiterung
Abbildung 12: Reduktion und Erweiterung
Sicherheit geben
Damit Kinder sich trauen, sich aktiv an der Reflexionsphase zu beteiligen, können verschiedene Aspekte dazu führen, dass sie sich sicherer fühlen, zum Beispiel:
-
Transparenz über Ablauf und Methoden geben (siehe Abbildung 12)
-
bereits vor Präsentation der Ergebnisse Austausch über Lösungen in Tandems / Mathekonferenzen ermöglichen
-
in Tandems oder Gruppen präsentieren lassen
-
Ergebnisse würdigen
-
Fehler sinnvoll aufgreifen
-
nur Inhalte aus der Stunde aufgreifen und keine neuen einbringen
-
Sprachspeicher zur Unterstützung beim Nachvollziehen und bei der Versprachlichung nutzen.
 Abbildung 13: Transparenz
Abbildung 13: Transparenz
Video zu Umsetzung der Differenzierungsmaßnahmen
Die folgende Übersicht zeigt die im Video dargestellten Inhalte. Ein Klick auf das Pluszeichen führt jeweils zu dem dargestellten Material:
Gespeichert von anna.koester_30508 am Mi, 02/12/2025 - 14:57
Abbildung 14: Material Differenzierungsmaßnahmen
Das gesamte Material dieser Seite können Sie hier gebündelt herunterladen
Materialpaket - Subtraktion am Rechenstrich