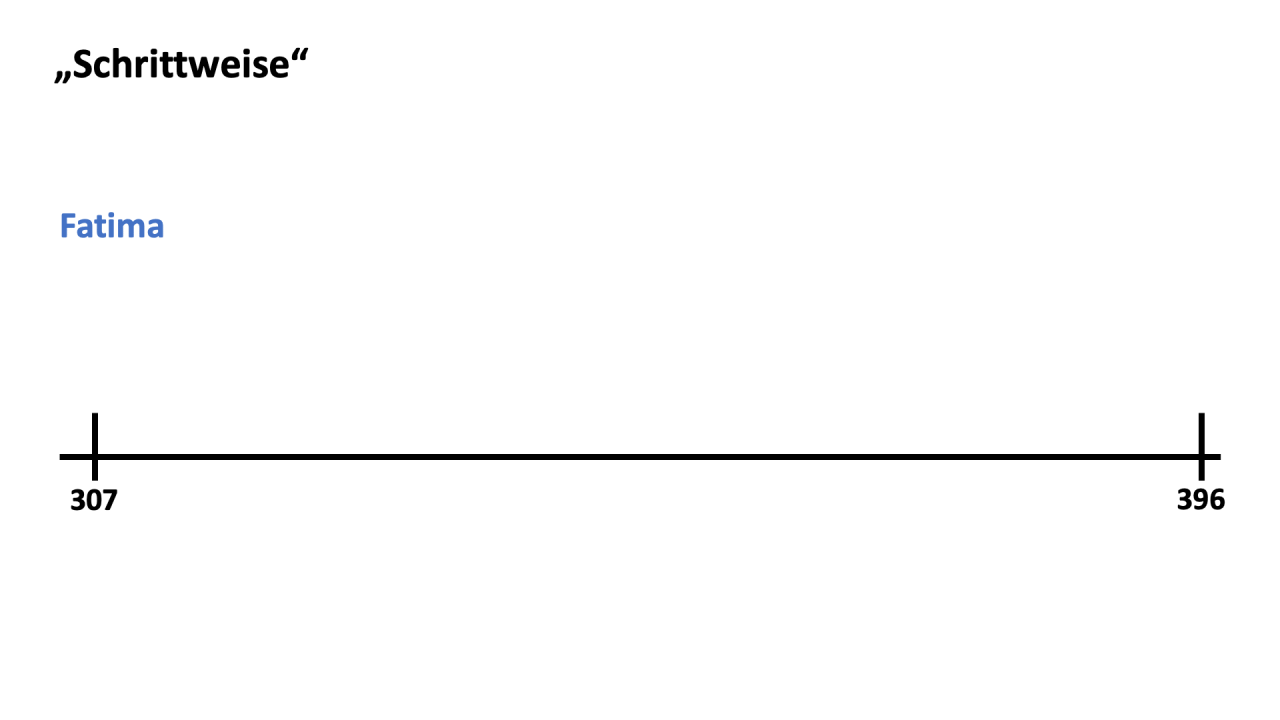Aufgabenstellung kompakt "Subtraktionsaufgaben am Rechenstrich"

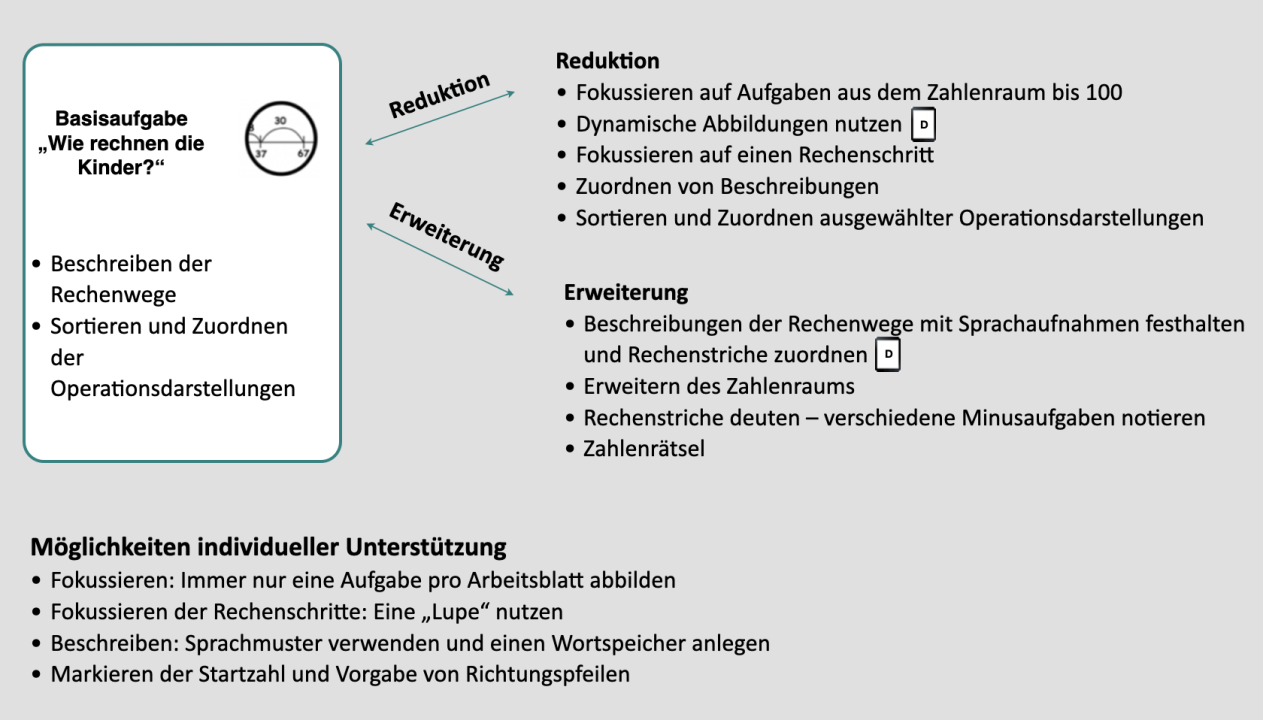
Die Übersicht zeigt die Basisaufgabe und Möglichkeiten der Erweiterung, Reduktion und Möglichkeiten der individuellen Unterstützung. „Basisaufgabe: „Wie rechnen die Kinder?“ Beschreiben der Rechenwege. Sortieren und Zuordnen von Operationsdarstellungen. Reduktion: Fokussieren auf Aufgaben aus dem Zahlenraum bis 100. Fokussieren auf einen Rechenschritt. Zuordnen von Beschreibungen. Sortieren und Zuordnen ausgewählter Operationsdarstellungen. Erweiterung: Erweitern des Zahlenraumes. Rechenstriche deuten – verschiedene Minusaufgaben notieren. Zahlenrätsel. Möglichkeiten individueller Unterstützung: Fokussieren: Immer nur eine Aufgabe pro Arbeitsblatt abbilden. Fokussieren der Rechenschritte: Eine „Lupe“ nutzen. Beschreiben: Sprachmuster verwenden und einen Wortspeicher anlegen. Markieren der Startzahl und Vorgabe von Richtungspfeilen.“
Abbildung 1: Übersicht_Aufgabenstellung kompakt "Subtraktionsaufgaben"

Download Übersicht

Basisaufgabe

"Wie rechnen die Kinder?"

Material: Karten mit verschiedenen Darstellungen einer Subtraktionsaufgabe am Rechenstrich, Heft, Stift

Der Schwerpunkt der Aufgabenstellung liegt auf dem Erkunden und Deuten von Operationsdarstellungen am Rechenstrich sowie auf dem flexiblen Übersetzen zwischen verschiedenen Operationsdarstellungen.

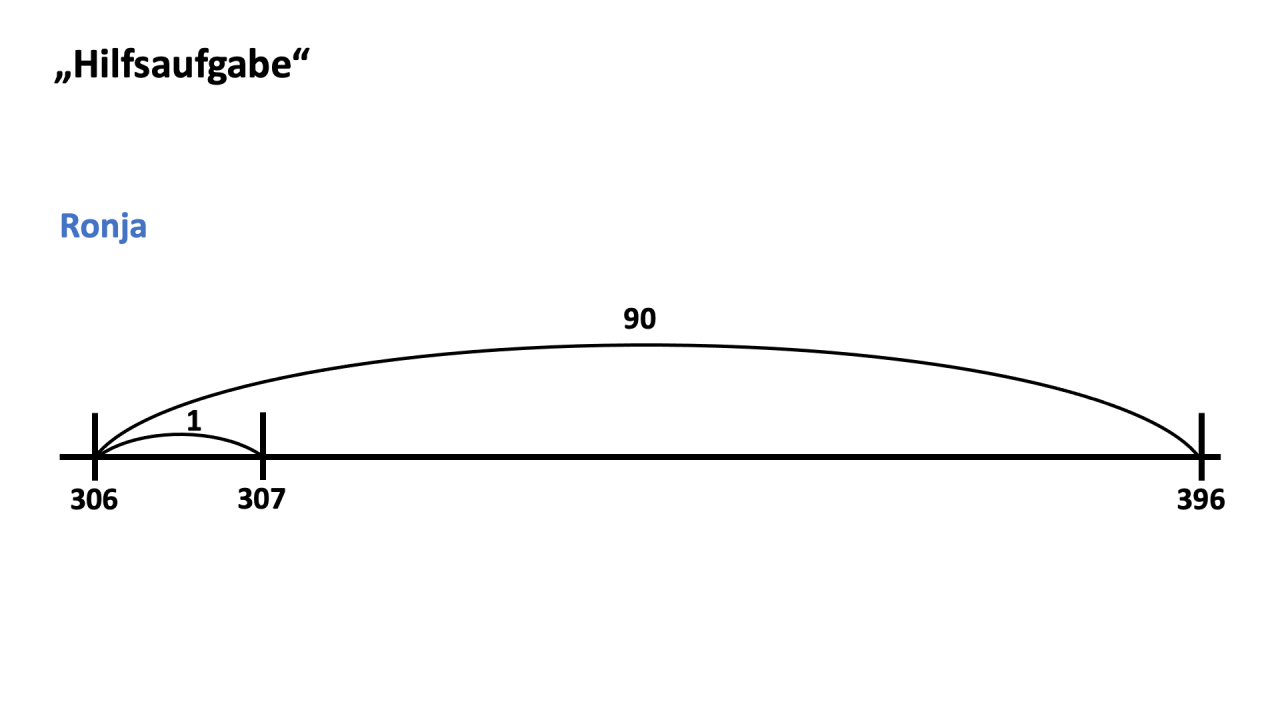
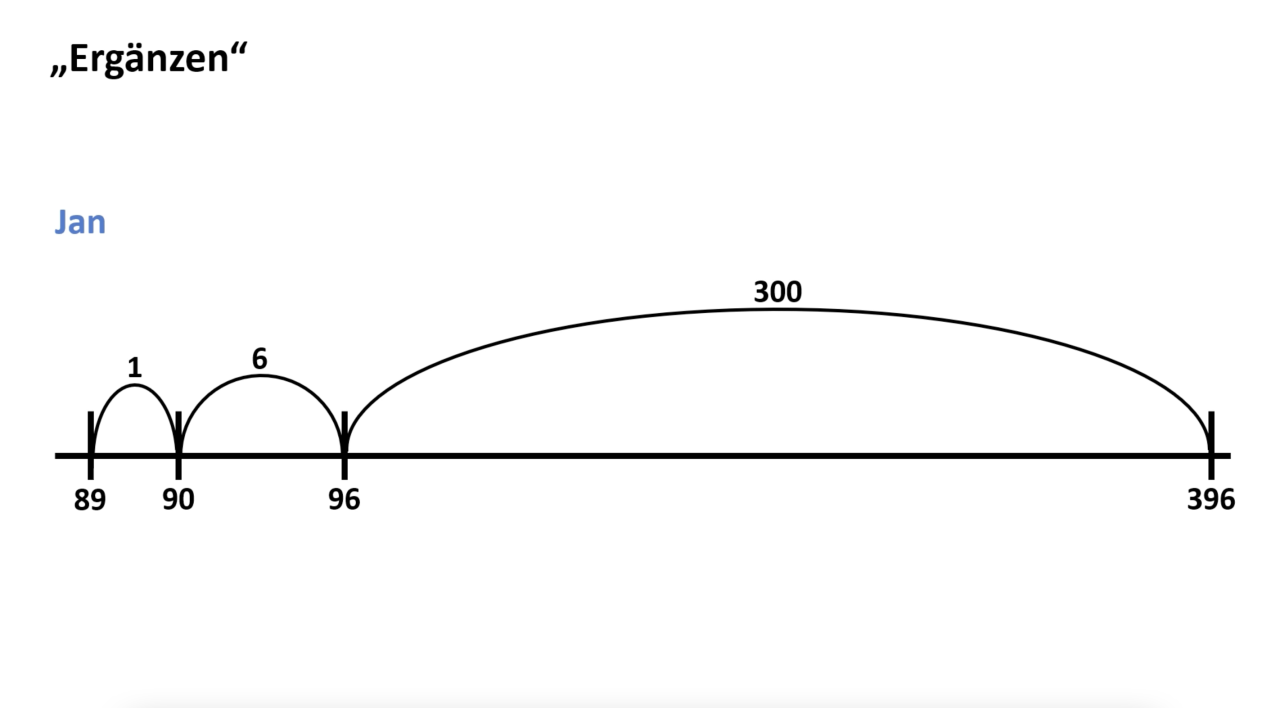
Die Kinder erhalten Aufgabenkarten mit Darstellungen von möglichen Rechenwegen einer Subtraktionsaufgabe am Rechenstrich (beispielsweise 396 - 89).

Beispiele für Aufgabenkarten:

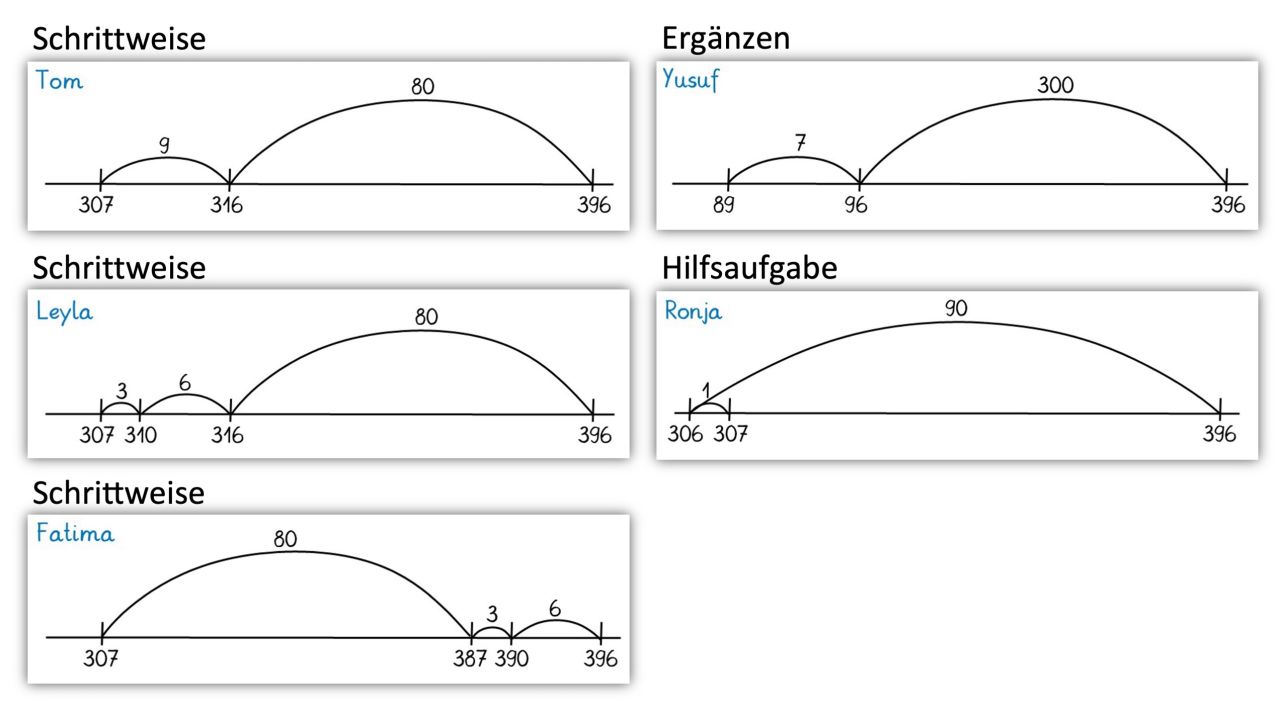
6 Karten mit unterschiedlichen Lösungen der Subtraktionsaufgabe 396 minus 89 am Rechenstrich. 1. Karte Ronja: „Hilfsaufgabe“: Rechenstrich mit den Zahlen 306, 307 und 396. Die Zahlen 306 und 396 sind mit einem Bogen verbunden und mit 90 markiert. Die Zahlen 306 und 307 sind mit einem Bogen verbunden und mit 1 markiert. 2. Karte Fatima: „Schrittweise“: Rechenstrich mit den Zahlen 307, 387, 390 und 396. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 80, 3 und 6. 3. Karte Tom: „Schrittweise“: Rechenstrich mit den Zahlen 307, 316 und 396. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 9 und 80. 4. Karte Leyla: „Schrittweise“: Rechenstrich mit den Zahlen 307, 310, 316 und 396. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 3, 6 und 80. 5. Karte Yusuf: „Ergänzen“: Rechenstrich mit den Zahlen 89, 96 und 396. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 7 und 300. 6. Karte Jan: „Ergänzen“: Rechenstrich mit den Zahlen 89, 90, 96 und 396. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 1, 6 und 300.
Abbildung 2

Die Aufgabenstellung lautet:

"Wie rechnet Tom (Leyla, Yusuf, Jan, …)? Schreibe die Rechenschritte auf."

Die Kinder notieren die zugehörige Subtraktionsaufgabe und dokumentieren ausführlich die verschiedenen Rechenschritte ("Übersetzen" einer anschaulichen Operationsdarstellung am Rechenstrich in eine schriftlich-symbolische Operationsdarstellung).

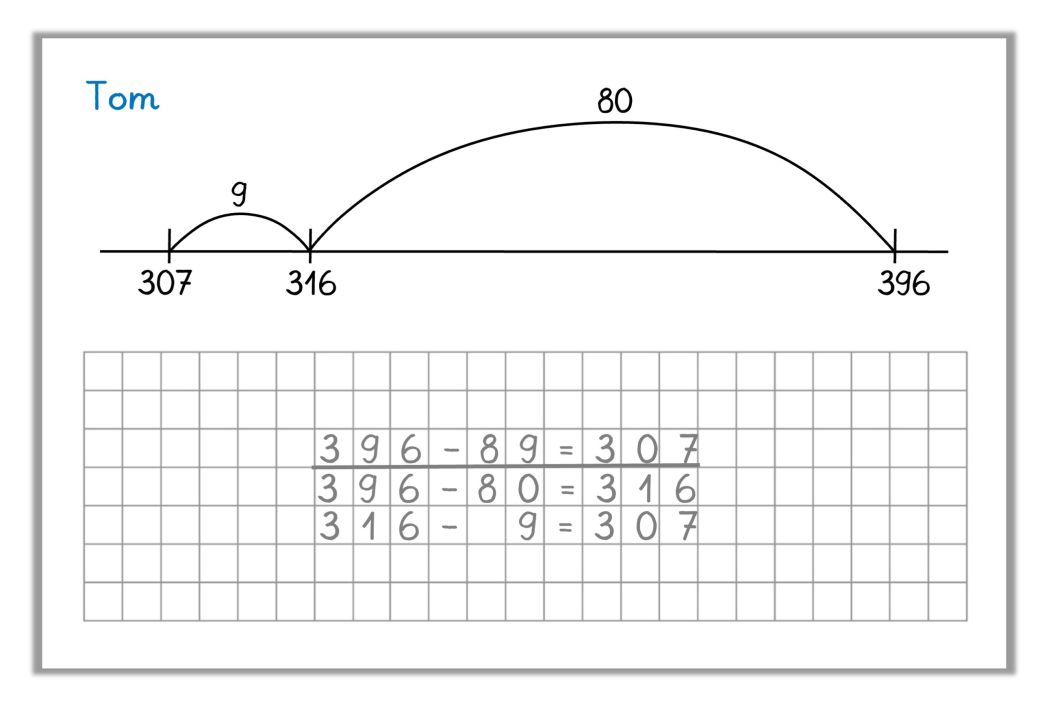
Karte Tom. Rechenstrich mit den Zahlen 307, 316 und 396. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 9 und 80. Darunter Notation: 396 minus 89 = 307, darunter Rechenschritte 396 minus 80 = 316, 316 minus 9 = 307.
Abbildung 3

 

Wichtig: 

Die Strategie „Hunderter, Zehner und Einer extra“ ist am Rechenstrich nicht darstellbar.

Werden auch die Karten mit der Strategie "Ergänzen" eingesetzt, sollten sich die Kinder bereits im Vorfeld mit dieser Strategie auseinandergesetzt haben.

Vertiefung

Beschreiben der Rechenwege

Material: Karten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich, Karten mit in Teilen vorgegebenen Beschreibungen; Stift

Eine Möglichkeit, Rechenwege beschreiben zu lassen, bietet sich nach der Bearbeitung der Basisaufgabe.

Die Kinder notieren eigene Beschreibungen zu den Rechenwegen bzw. ergänzen in Teilen vorgegebene Beschreibungen

("Übersetzen" einer anschaulichen bzw. schriftlich-symbolischen Operationsdarstellung in eine verbal-symbolische).

Wichtig:

Das Beschreiben von Rechenwegen sollte im Vorfeld thematisiert und geübt werden. Eine Hilfe kann hierbei das Anlegen eines Wortspeichers und das Aufgreifen bzw. Aufzeigen von Sprachmustern sein (vgl. "Möglichkeiten individueller Unterstützung").

Aufgabenstellung:

"Wie rechnet Tom? Beschreibe!"

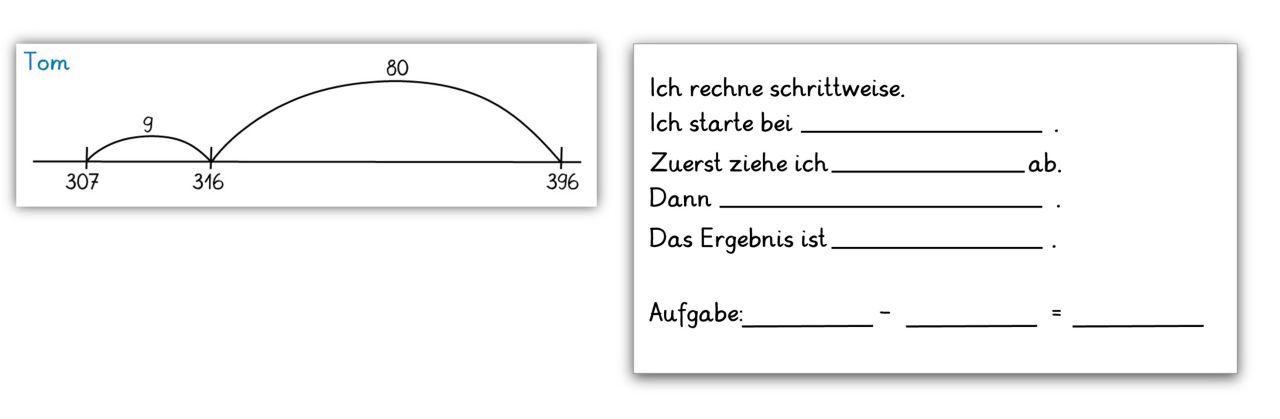
Links: Aufgabenkarte „Tom“ (siehe Abbildung 3). Rechts daneben Karte mit in Teilen vorgegebenen Beschreibung: „Ich rechne schrittweise. Ich starte bei _. Zuerst ziehe ich _ ab. Dann _. Das Ergebnis ist _. Aufgabe: _ minus _= _.“
Abbildung 4

Vertiefung

Sortieren und Zuordnen von Operationsdarstellungen

Material: Sortiertafel / Karten mit verschiedenen Operationsdarstellungen (Subtraktionsaufgaben)

Vertiefend können die Kinder angeregt werden, Operationsdarstellungen zur Subtraktion zu sortieren und einander zuzuordnen. Die Kinder erhalten neben Karten mit Darstellungen von Subtraktionsaufgaben am Rechenstrich noch weitere Darstellungen von Subtraktionsaufgaben (z. B.: schriftlich-symbolische und verbal-symbolische) sowie eine Sortiertafel.

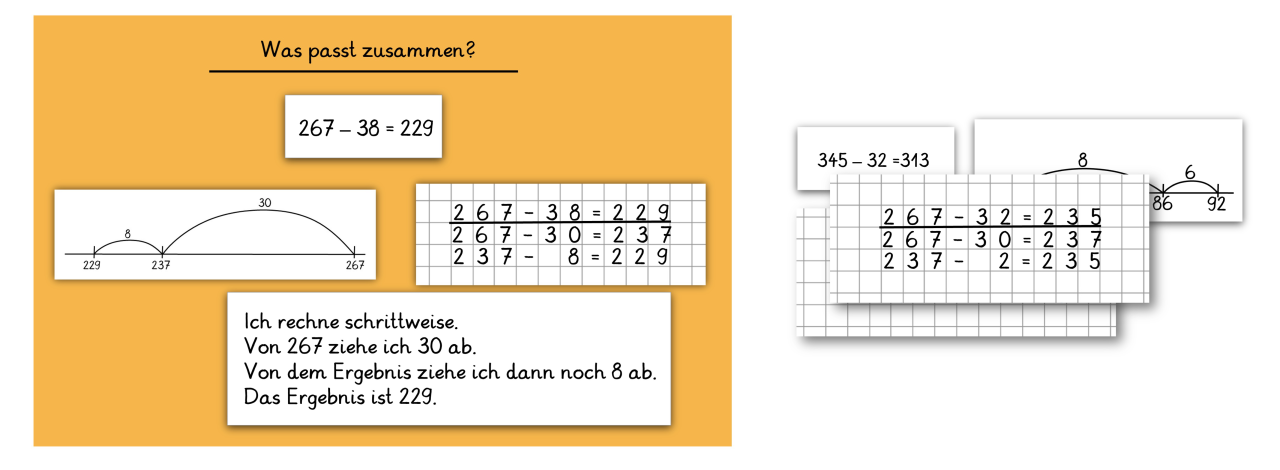
Links Sortiertafel. Überschrift: „Was passt zusammen?“ Darunter 4 Karten mit verschiedenen Darstellungen: 1. „267 minus 38 = 229“. 2. Rechenstrich mit den Zahlen 229, 237 und 267. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. 3. Halbschriftliche Subtraktion zur Aufgabe 267 minus 38 = 229, darunter die Rechenschritte: 267 minus 30 = 237, 237 minus 8 = 229. 4. Sprachliche Beschreibung des Vorgehens: „Ich rechne schrittweise. Von 267 ziehe ich 30 ab. Von dem Ergebnis ziehe ich dann noch 8 ab. Das Ergebnis ist 229.“ Rechts: Stapel mit weiteren Karten in verschiedenen Darstellungen zu anderen Aufgaben.
Abbildung 5

Reduktion

Fokussieren auf Aufgaben aus dem Zahlenraum bis 100

Material: Karten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich, Heft, Stift

Eine Reduktion der Komplexität der Basisaufgabe sowie der vertiefenden Aufgabenstellungen kann (unter anderem) durch die Beschränkung auf Aufgaben aus dem Zahlenraum bis 100 ermöglicht werden.

Beispiel:

Die Kinder erhalten Aufgabenkarten mit verschiedenen Darstellungen einer Subtraktionsaufgabe am Rechenstrich (beispielsweise 96 - 89). Die Aufgabe sollte in einem Zusammenhang mit der für die Basisaufgabe gewählten Subtraktionsaufgabe stehen:

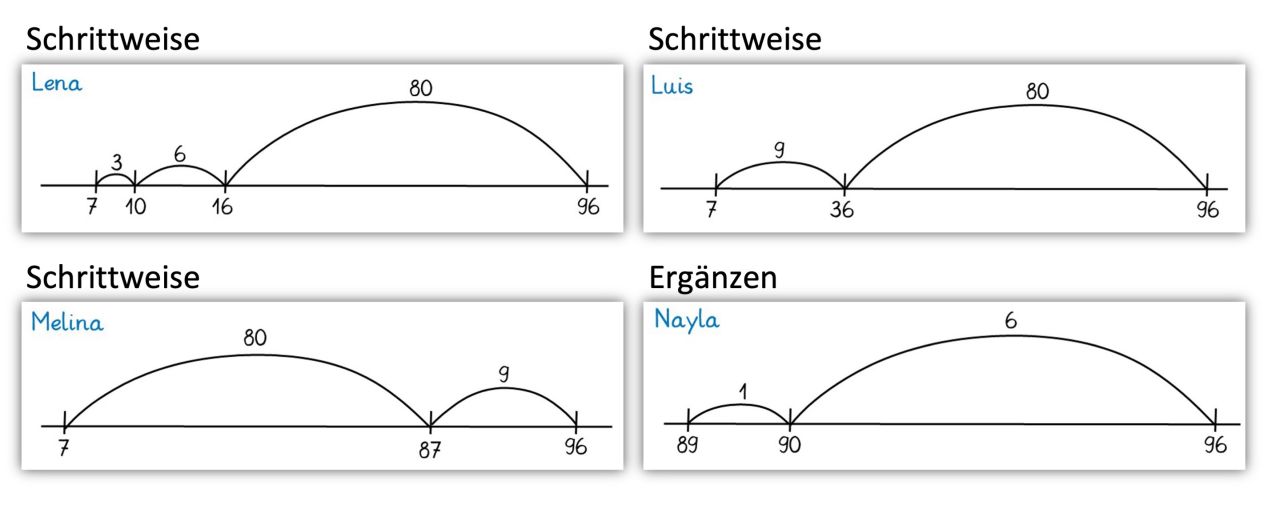
4 Karten mit unterschiedlichen Lösungen der Subtraktionsaufgabe 96 minus 89 am Rechenstrich. Aufgabenkarte Lena: „Schrittweise“: Rechenstrich mit den Zahlen 7, 10, 16 und 96. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 3, 6, 80. Karte Luis: „Schrittweise“: Rechenstrich mit den Zahlen 7, 16, 96. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 9 und 80. Karte Melina: „Schrittweise“: Rechenstrich mit den Zahlen 7, 87 und 96. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 80 und 9. Karte Nayla: „Ergänzen“: Rechenstrich mit den Zahlen 89, 90 und 96. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 1 und 6.
Abbildung 6

Analog zur vertiefenden Aufgabenstellung "Sortieren und Zuordnen von Operationsdarstellungen" sortieren die Kinder Aufgabenkarten mit verschiedenen Operationsdarstellungen aus dem Zahlenraum bis 100:

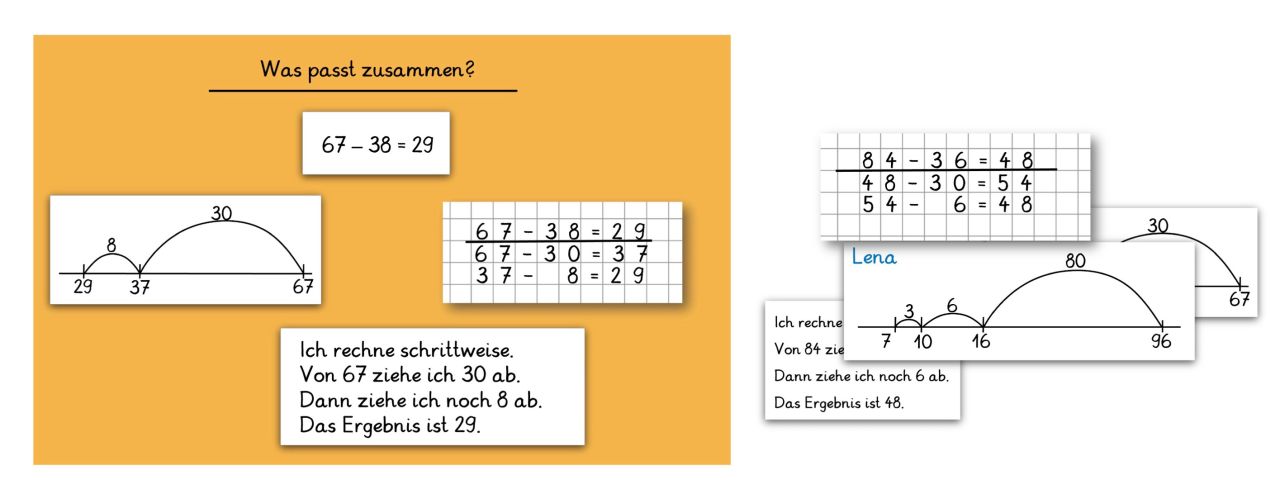
Links: Sortiertafel. Überschrift: „Was passt zusammen?“ Darunter 4 Karten mit verschiedenen Darstellungen: 1. „67 minus 38 = 29“. 2. Rechenstrich mit den Zahlen 29, 37 und 67. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. 3. Halbschriftliche Subtraktion zur Aufgabe 67 minus 38 = 29, darunter Rechenschritte: 67 minus 30 = 37, 37 minus 8 = 29. 4. Karte mit Versprachlichung des Vorgehens: „Ich rechne schrittweise. Von 67 ziehe ich 30 ab. Von dem Ergebnis ziehe ich dann noch 8 ab. Das Ergebnis ist 29.“
Abbildung 7

Reduktion

Dynamische Abbildungen nutzen

Anstelle von Aufgabenkarten können den Kindern auch kurze Videos bzw. dynamische Abbildungen des Rechenstrichs nutzen (s. unten). Die Vorgehensweisen am Rechenstrich werden dynamisch und Schritt für Schritt eingeblendet, sodass die Kinder diese langsam nachvollziehen können. Anschließend können die Kinder die beobachteten Vorgehensweisen beschreiben. („Wie ist das Kind vorgegangen? Beschreibe.“) Die kurzen Videos können vorab mit PowerPoint (Vorlage) erstellt und mit geringem Aufwand für die Lerngruppe adaptiert werden. 

 
Dynamische Abbildung (GIF): Hilfsaufgabe
 
 
Dynamische Abbildung (GIF): Ergänzen
 
 
Dynamische Abbildung (GIF): Schrittweise
 

Vorlage Powerpoint Erstellung von dynamischen Abbildungen (kurzen Videos)

Reduktion

Fokussieren auf einen Rechenschritt

Material: Karten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich, "Lupe", Heft, Stift

Durch Abdecken eines Teiles des Rechenstriches kann der Fokus auf einen Rechenschritt gelenkt werden. Die Kinder notieren nur die "sichtbare" Subtraktionsaufgabe.

Aufgabenstellung:

"Schreibe eine passende Minusaufgabe."

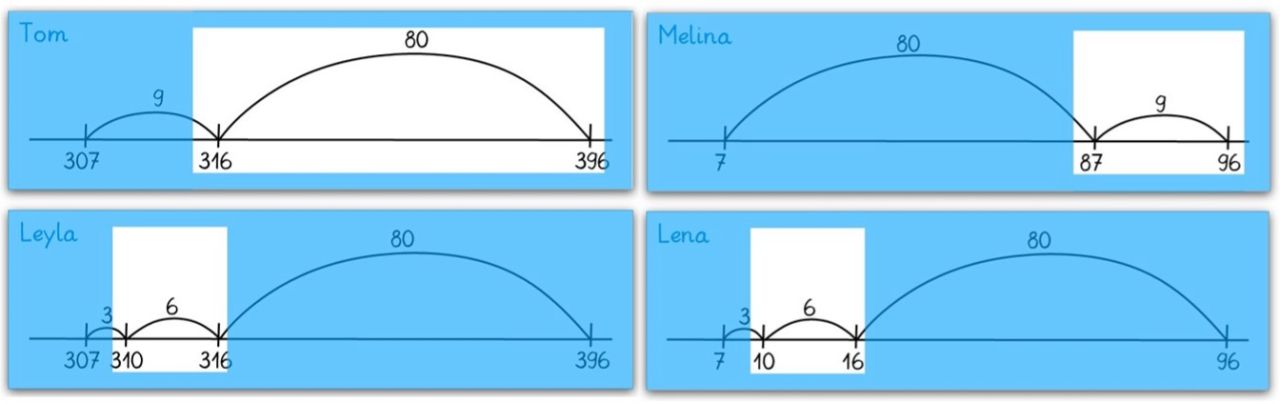
4 Karten mit Darstellungen von möglichen Rechenwegen der Subtraktionsaufgabe 396 minus 89 am Rechenstrich. Mittels eines Sichtfensters ist jeweils nur ein Rechenschritt sichtbar. Im Folgenden wird nur das Sichtfenster beschrieben. 1. Die Zahlen 316 und 396 sind auf dem Rechenstrich eingetragen, mit einem Bogen verbunden und mit 80 markiert. 2. Die Zahlen 87 und 96 sind auf dem Rechenstrich eingetragen, mit einem Bogen verbunden und mit 9 markiert. 3. Die Zahlen 310 und 316 sind auf dem Rechenstrich eingetragen, mit einem Bogen verbunden und mit 6 markiert. 4. Die Zahlen 10 und 16 sind auf dem Rechenstrich eingetragen, mit einem Bogen verbunden und mit 6 markiert.
Abbildung 8

Reduktion

Zuordnen von Beschreibungen

Material: Karten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich, Karten mit vorgegebenen Beschreibungen

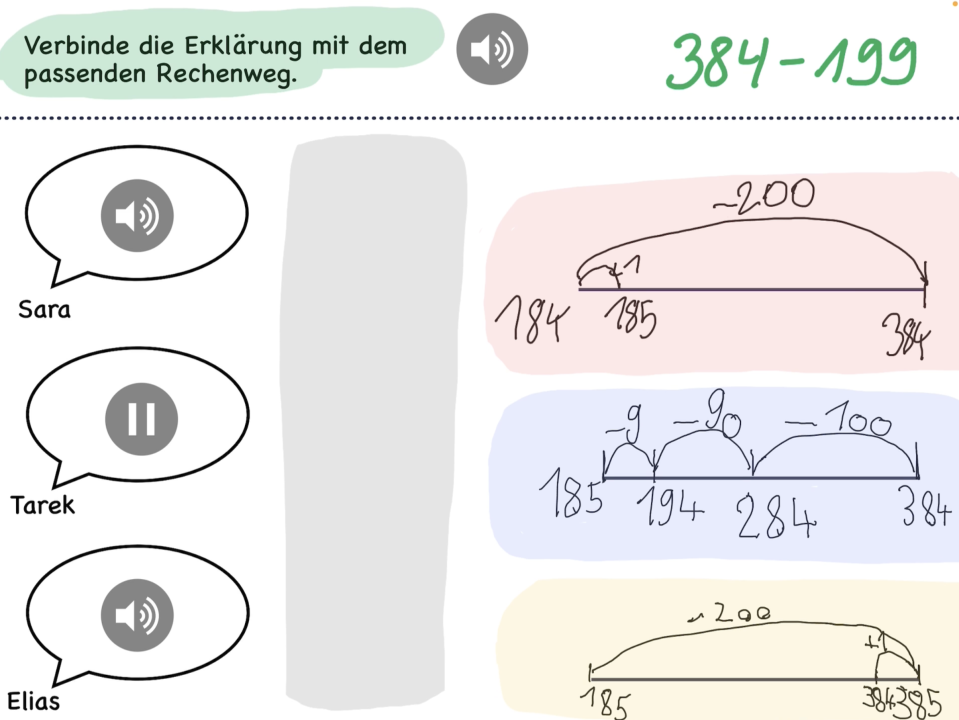
Alternativ zur Bearbeitung der vertiefenden Aufgabenstellung "Beschreiben und Dokumentieren der Rechenwege" ordnen die Kinder vorgegebene Aufgabenbeschreibungen den Darstellungen auf dem AB zu.

("Übersetzen" einer anschaulichen bzw. schriftlich-symbolischen Operationsdarstellung in eine verbal-symbolische).

Auch hierbei ist wichtig, dass die Kinder sich bereits im Vorfeld mit Möglichkeiten der Beschreibung auseinandergesetzt haben (vgl. hierzu "Möglichkeiten individueller Unterstützung" - Sprachmuster verwenden und einen Wortspeicher anlegen).

Aufgabenstellung:

"Welche Beschreibung passt?"

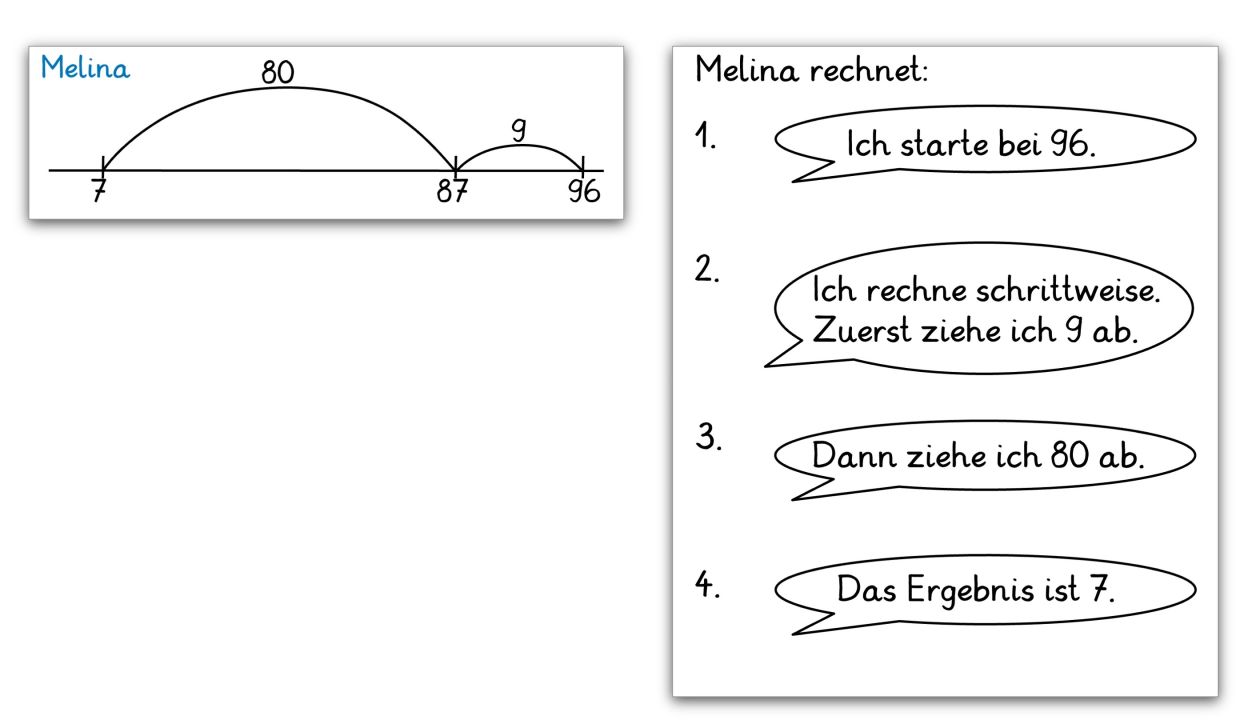
Links Karte mit Darstellung der Aufgabe 96 minus 89 am Rechenstrich (Melina). Die Zahlen 7, 87 und 96 sind eingetragen, mit einem Bogen verbunden und mit der jeweiligen Differenz gekennzeichnet: 80 und 9. Rechts daneben Karte mit Beschreibungen. Oben: „Melina rechnet:“, darunter Sprechblasen: „1. Ich starte bei 96. 2. Ich rechne schrittweise. Zuerst ziehe ich 9 ab. 3. Dann ziehe ich 80 ab. 4. Das Ergebnis ist 7.“
Abbildung 9

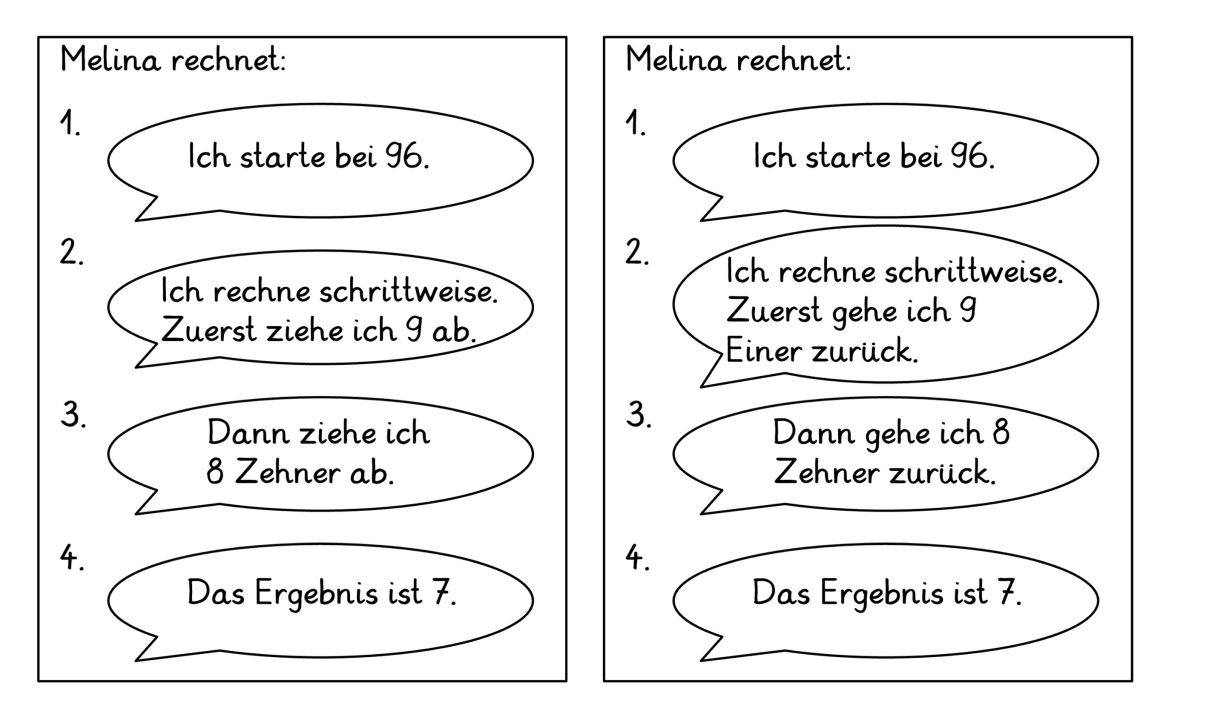
Alternative Beschreibungen:

2 Karten mit Beschreibungen von Rechenwegen nebeneinander, oben jeweils: „Melina rechnet:“, darunter Beschreibung der 4 Rechenschritte. Links: „1. Ich starte bei 96. 2. Ich rechne schrittweise. Zuerst ziehe ich 9 Einer ab. 3. Dann ziehe ich 8 Zehner ab. 4. Das Ergebnis ist 7.“ Rechts: „Ich rechne schrittweise. Zuerst gehe ich 9 Einer zurück. 3. Dann gehe ich 8 Zehner zurück. 4. Das Ergebnis ist 7.“
Abbildung 10

Reduktion

Sortieren und Zuordnen ausgewählter Operationsdarstellungen

Material: Sortiertafel, Karten mit verschiedenen Operationsdarstellungen (Subtraktionsaufgaben)

Während bei der vertiefenden Aufgabenstellung "Sortieren und Zuordnen von Operationsdarstellungen" zugleich mehrere verschiedene Operationsdarstellungen einander zugeordnet werden, liegt der Schwerpunkt im Bereich der Reduktion auf der Zuordnung von jeweils zwei (ausgewählten) Operationsdarstellungen.

Die Auswahl der vorgegebenen Darstellungen ist abhängig von den individuellen Zielsetzungen sowie den jeweiligen Lernvoraussetzungen der einzelnen Kinder.

Beispiel 1:

Zuordnung von Darstellungen am Rechenstrich und schriftlich-symbolischen Notationen von Rechenwegen.

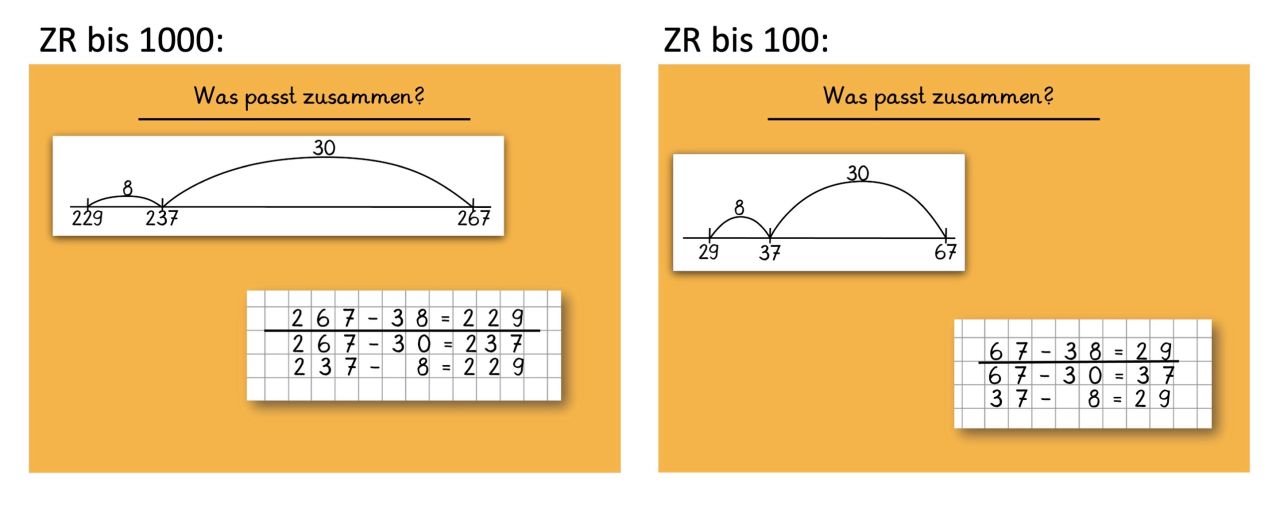
Zwei Sortiertafeln nebeneinander. Oben links: „ZR bis 1000“, rechts: „ZR bis 100“. Überschrift jeweils: „Was passt zusammen?“ Darunter jeweils zwei Aufgabenkarten. Links: 1. Rechenstrich mit den Zahlen 229, 237 und 267. Die Zahlen wurden mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. 2. Halbschriftliche Subtraktion: „267 minus 38 = 229“, darunter „267 minus 30 = 237 und 237 minus 8 = 229“. Rechts: 1. Rechenstrich mit den Zahlen 29, 37 und 67. Die Zahlen wurden mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. 2. Halbschriftliche Subtraktion: „67 minus 38 = 29“, darunter 67 minus 30 = 37 und 37 minus 8 = 29“.
Abbildung 11

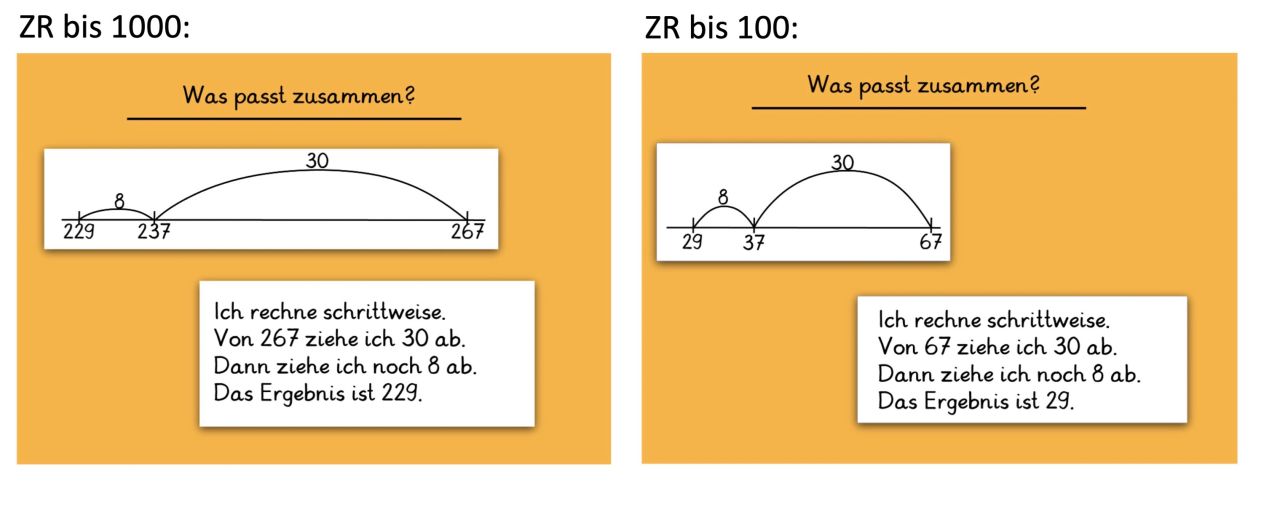
Beispiel 2:

Zuordnung von Darstellungen am Rechenstrich und Beschreibungen von Rechenwegen (verbal-symbolisch).

Zwei Sortiertafeln nebeneinander. Oben links: „ZR bis 1000“, rechts: „ZR bis 100“. Überschrift jeweils: „Was passt zusammen?“ Darunter jeweils zwei Aufgabenkarten. Links: 1. Rechenstrich mit den Zahlen 229, 237 und 267. Die Zahlen wurden mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. 2. Beschreibung: „Ich rechne schrittweise. Von 267 ziehe ich 30 ab. Dann ziehe ich noch 8 ab. Das Ergebnis ist 229.“ Rechts: 1. Rechenstrich mit den Zahlen 29, 37 und 67. Die Zahlen wurden mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. 2. Beschreibung: „Ich rechne schrittweise. Von 67 ziehe ich 30 ab. Dann ziehe ich noch 8 ab. Das Ergebnis ist 29.“
Abbildung 12
 

Erweiterung

Beschreibungen der Rechenwege mit Sprachaufnahmen festhalten und Rechenstriche zuordnen

Die Beschreibungen der Rechenwege können von den Schüler:innen mittels Sprachaufnahmen (z. B. mit der App Book Creator, verfügbar auf iOS-Geräten, Stand Januar 2023) festgehalten und dokumentiert werden. Dabei sollten die Kinder versuchen, die Rechenwege möglichst genau und mit Fachsprache zu beschreiben. In Partner:innenarbeit können die Kinder anschließend die Sprachaufnahmen gegenseitig anhören und Darstellungen am Rechenstrich zuordnen oder das Gehörte direkt als Rechenweg auf einem leeren Rechenstrich umsetzen. Auch in der Klasse können die Sprachaufnahmen in einer Reflexionsphase angehört und dabei Kriterien gelungener Beschreibungen von Rechenwegen reflektiert werden.

Im Video sehen und hören Sie in einer  beispielhafte Schülerlösung, wie Kinder Ihre Rechenwege im Book Creator beschreiben und darstellen. 

 
Video: Schülerlösungen zu Rechenwege im Book Creator darstellen

Erweiterung

Erweitern des Zahlenraumes

Material: Karten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich, Heft, Stift

Die vorgegebenen Subtraktionsaufgaben beschränken sich nicht nur auf den Zahlenraum bis 1000, sondern gehen auch darüber hinaus:

Dabei stehen die Aufgaben in einem Zusammenhang mit den gegebenen Subtraktionsaufgaben aus dem Zahlraum bis 1000.

4 verschiedene Karten mit Darstellungen von möglichen Rechenwegen von Subtraktionsaufgaben am Rechenstrich. 2 Karten zu 5496 minus 3289: 1. Karte Till: „Schrittweise“: Rechenstrich mit den Zahlen 2207, 2216, 2296, 2496 und 5496. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz markiert: 9, 80, 200 und 3000. 2. Karte Leandro: „Schrittweise“: Rechenstrich mit den Zahlen 2207, 5207, 5407, 5487 und 5496. Die Zahlen sind mit Bögen miteinander verbunden und mit der jeweiligen Differenz gekennzeichnet: 3000, 200, 80, 9. 1 Karte zu 5496 minus 2207: 3. Karte Maren: „Ergänzen“: Rechenstrich mit den Zahlen 3289, 3296, 3496 und 5496. Die Zahlen sind mit Bögen miteinander verbunden und mit der jeweiligen Differenz gekennzeichnet: 7, 200 und 2000. 1 Karte zu 5496 minus 3289: 4. Karte Jasemin: „Hilfsaufgabe“: Rechenstrich mit den Zahlen 2196, 2207 und 5496. Die Zahlen 2196 und 5496 sind mit einem Bogen verbunden und mit 3300 markiert. Die Zahlen 2196 und 2207 sind mit einem Bogen verbunden und mit 11 markiert.
Abbildung 14

Analog zur Basisaufgabe notieren die Kinder die Rechenschritte.

Aufgabenstellung:

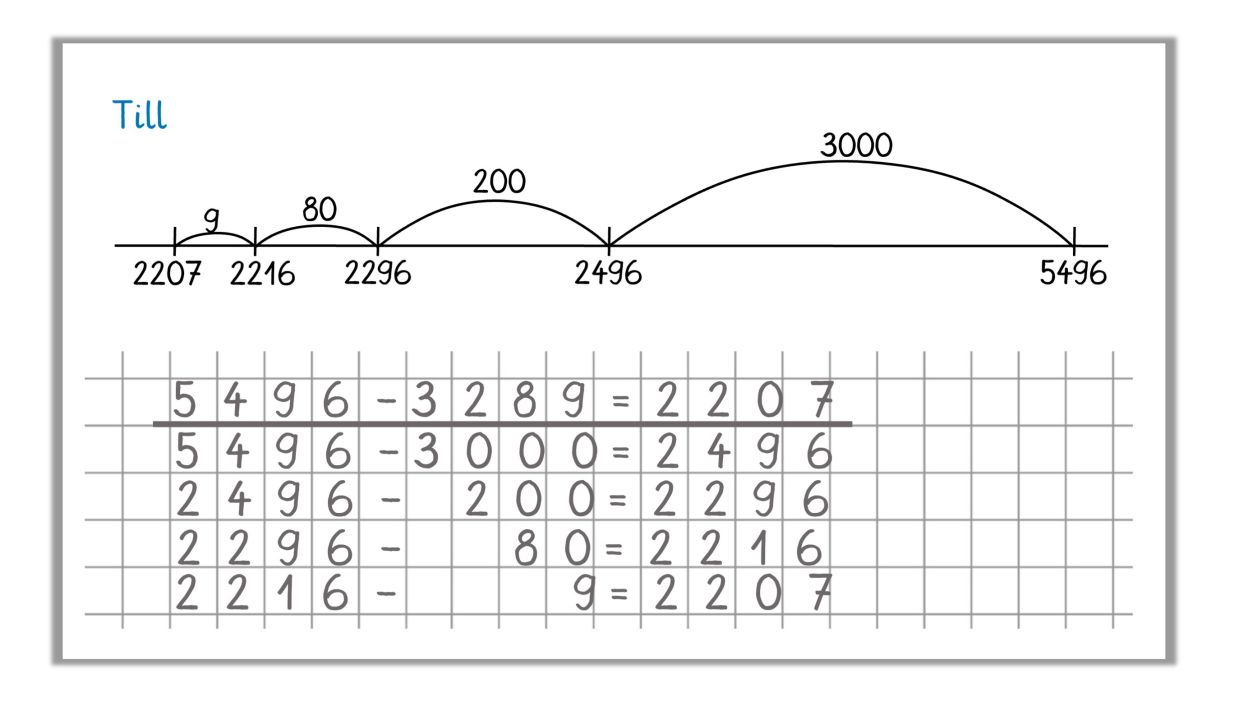
"Wie rechnet Till (Leandro, Maren, ...)? Schreibe die Rechenschritte auf."

Mögliche Notation:

Karte Till. Darstellung der Aufgabe 5496 minus 3289 am Rechenstrich mit den Zahlen 2207, 2216, 2296, 2496 und 5496. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz markiert: 9, 80, 200 und 3000. Darunter halbschriftliche Subtraktion: „5496 minus 3289 = 2207“, darunter Rechenschritte: „5496 minus 3000 = 2496, 2496 minus 200 = 2296, 2296 minus 80 = 2216, 2216 minus 9 = 2207“.
Abbildung 15

Erweiterung

Rechenstriche deuten - verschiedene Minusaufgaben notieren

Material: Karten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich, Heft, Stift

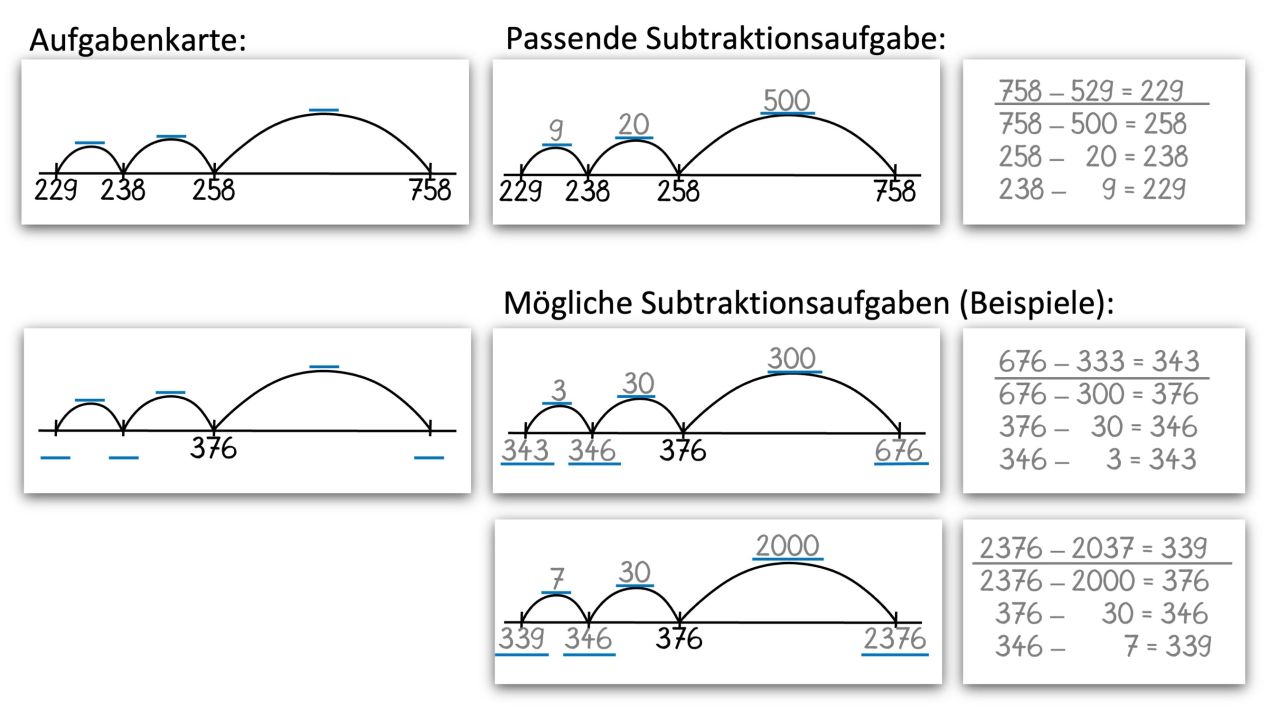
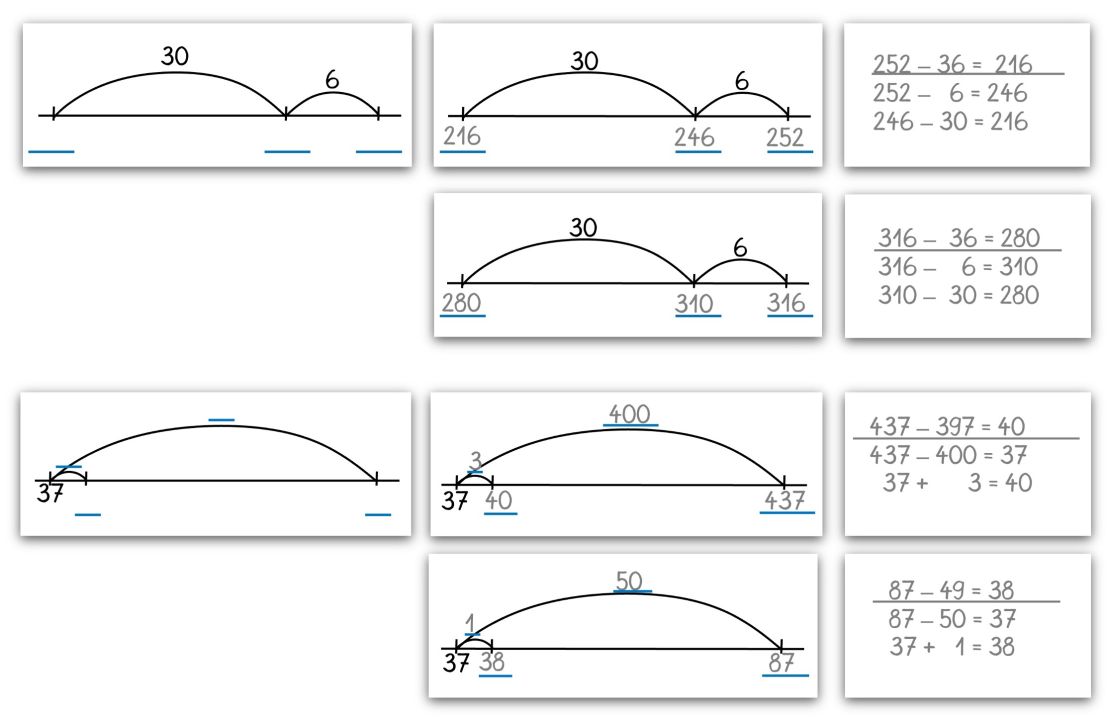
Die Kinder erhalten verschiedene Darstellungen von Aufgaben am Rechenstrich. Fehlende Zahlen am Rechenstrich (bzw. an den Bögen) sollen ergänzt, die zugehörigen Subtraktionsaufgaben und die einzelnen Rechenschritte notiert werden.

Einige der Rechenstriche sind mehrdeutig interpretierbar und passen zu verschiedenen Aufgaben. Der Zahlraum, in dem sich die Kinder bewegen, ist freigestellt. D. h., unterschiedliche Lösungen sind möglich und erwünscht.

Links: Aufgabenkarten mit verschiedenen Darstellungen von Subtraktionsaufgaben am Rechenstrich mit fehlenden Zahlen. Rechts daneben Karten mit möglichen Lösungen für die Aufgabenkarte und der jeweiligen Notation der Rechenschritte. 1. Aufgabenkarte: Rechenstrich mit den Zahlen 229, 238, 258 und 758. Die Zahlen sind mit Bögen verbunden. Über den Bögen steht jeweils ein Fragezeichen. Rechts daneben Karte „passende Subtraktionsaufgabe“: Ergänzte Zahlen über den Bögen: 9, 20, und 500. Rechts daneben schriftliche Notation: „758 minus 529 = 238“, darunter „758 minus 500 = 258, 258 minus 20 = 238, 238 minus 9 = 238“. 2. Aufgabenkarte: Rechenstrich mit 4 eingezeichneten Strichen und 3 Bögen. Unter dem dritten Strich steht die Zahl 376. Unter den übrigen Strichen sowie über den Bögen sind jeweils Fragezeichen. Rechts daneben 2 Beispiele möglicher Subtraktionsaufgaben: 1. Ausgefüllte Aufgabenkarte: Die Zahlen 343, 346 und 676 wurden ergänzt. Über den Bögen stehen die Zahlen 3, 30 und 300. Rechts daneben schriftliche Notation: „676 minus 333 = 343“, darunter „676 minus 300 = 376, 376 minus 30 = 346, 346 minus 3 = 343“. 2. Ausgefüllte Aufgabenkarte: Die Zahlen 339, 346 und 2376. Über den Bögen stehen die Zahlen 3, 30 und 300. Rechts daneben schriftliche Notation „2376 minus 2037 = 339“, darunter „2376 minus 2000 = 376, 376 minus 30 = 346, 346 minus 7 = 339“.
Abbildung 16
3. Aufgabenkarte: Rechenstrich mit 3 eingezeichneten Strichen und 2 Bögen. Unter den Strichen sind Fragezeichen, über den Bögen die Zahlen 30 und 6. Rechts daneben 2 Beispiele möglicher Subtraktionsaufgaben: 1. Ausgefüllte Aufgabenkarte: Die Zahlen 216, 246 und 252 wurden eingetragen. Rechts daneben schriftliche Notation: „252 minus 36 = 216“, darunter „252 minus 6 = 246, 246 minus 30 = 216“. 2. Ausgefüllte Aufgabenkarte: Die Zahlen 280, 310 und 316 wurden eingetragen. Rechts daneben schriftliche Notation: „316 minus 36 = 280“, darunter „316 minus 6 = 310, 310 minus 30 = 280“. 4. Aufgabenkarte: Rechenstrich beginnend mit der Zahl 37. Von dort aus ein kleiner Bogen zu einem Fragezeichen und ein großer Bogen zu einem Fragezeichen. Über den Bögen stehen Fragezeichen. Rechts daneben 2 Beispiele möglicher Subtraktionsaufgaben: 1. Ausgefüllte Aufgabenkarte: Die Zahlen 40 und 87 wurden eingetragen. Über den Bögen die Zahlen 3 und 400. Rechts daneben schriftliche Notation: „437 minus 397 = 40“, darunter „437 minus 400 = 37, 37 + 3 = 40“. 2. Ausgefüllte Aufgabenkarte: Die Zahlen 38 und 87 wurden eingetragen. Über den Bögen die Zahlen 1 und 50. Rechts daneben schriftliche Notation: „87 minus 49 = 38“, darunter „87 minus 50 = 37, 37 + 1 = 38“.
Abbildung 17

Erweiterung

Zahlenrätsel

Material: Karten mit verschiedenen Zahlenrätseln, Heft, Stift

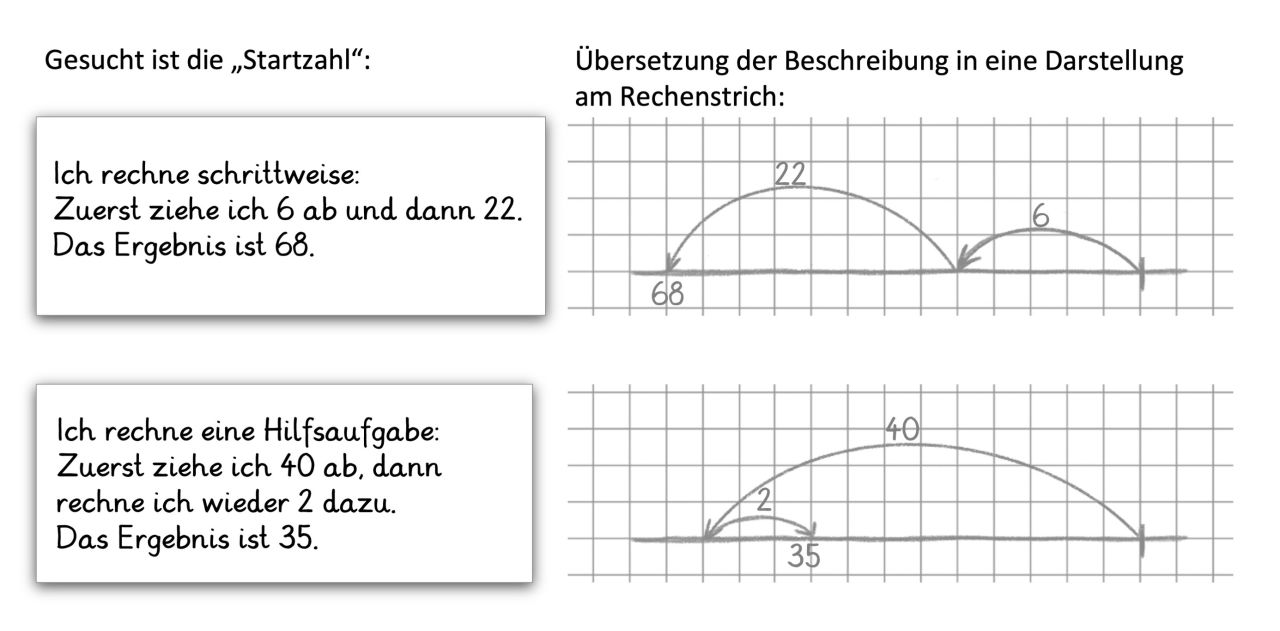
Ausgehend von einem "Zahlenrätsel" (Beschreibung eines Rechenweges), bei dem die Startzahl ermittelt werden soll, zeichnen die Kinder einen Rechenstrich, beschriften diesen und  notieren die zugehörige Subtraktionsaufgabe.

Gerechnet wird die Umkehraufgabe - ausgehend vom Ergebnis der Aufgabe muss addiert werden.

Mögliche Zahlenrätsel:

Links: „Gesucht ist die „Startzahl“:“, darunter zwei Aufgabenkarten mit Beschreibungen. Rechts: „Übersetzung der Beschreibung in eine Darstellung am Rechenstrich:“, darunter zwei Aufgabenkarten mit Rechenstrichen. 1. Beschreibung: „Ich rechne schrittweise. Zuerst ziehe ich 6 ab und dann 22. Das Ergebnis ist 68.“ Rechts daneben zugehöriger Rechenstrich: Rechts unbeschrifteter Strich, von dort ausgehend zwei Pfeile mit den Zahlen 6 und 22 nach links. Darunter steht die Zahl 68. 2. Beschreibung: „Ich rechne eine Hilfsaufgabe: Zuerst ziehe ich 40 ab, dann rechne ich wieder 2 dazu. Das Ergebnis ist 35.“ Rechts daneben zugehöriger Rechenstrich: Rechts unbeschrifteter Strich, von dort ausgehend ein langer Pfeil mit der Zahl 40 nach links zum Beginn des Rechenstrichs. Von dort ausgehend ein kleiner Pfeil mit der Zahl 2 nach rechts zur Zahl 35.
Abbildung 18

Im Anschluss können die Kinder zusätzlich angeregt werden, eigene Zahlenrätsel zu erfinden.

Möglichkeiten individueller Unterstützung

Fokussieren: Immer nur eine Aufgabe

Um die Fokussierung und Konzentration auf eine Aufgabe zu erleichtern, erhalten die Kinder Arbeitsblätter oder Arbeitskarten, auf denen jeweils nur eine Aufgabe abgebildet ist. Zusätzlich kann diese auch noch vergrößert dargestellt werden.

Möglichkeiten individueller Unterstützung

Fokussieren der einzelnen Rechenschritte: eine "Lupe" nutzen

Die Kinder arbeiten mit einer Folie ("Lupe") , durch die immer ein Rechenschritt in den Blick genommen wird.

Nach der Notation des ersten Rechenschrittes wird die Folie verschoben und der zweite Rechenschritt fokussiert und notiert.

Fokussieren des ersten Rechenschrittes.

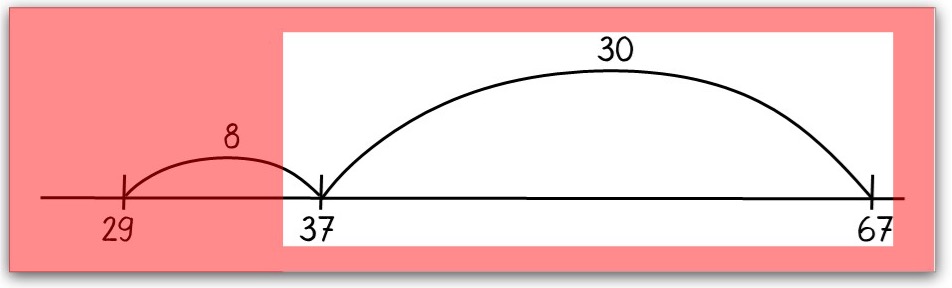
Karte mit Rechenstrich und Sichtfenster: Rechenstrich mit den Zahlen 29, 37 und 67. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. Fokussierter Bereich Karte 1: Rechenstrich mit den Zahlen 37 und 67. Über dem Bogen die Zahl 30.
Abbildung 19

Fokussieren des zweiten Rechenschrittes.

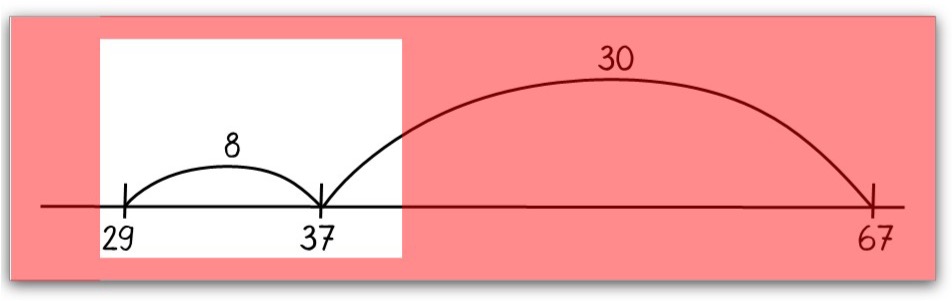
Karte mit Rechenstrich und Sichtfenster: Rechenstrich mit den Zahlen 29, 37 und 67. Die Zahlen sind mit Bögen verbunden und mit der jeweiligen Differenz gekennzeichnet: 8 und 30. Fokussierter Bereich Karte 2: Rechenstrich mit den Zahlen 29 und 37. Über dem Bogen die Zahl 8.
Abbildung 20

Möglichkeiten individueller Unterstützung

Beschreiben: Sprachmuster verwenden und einen Wortspeicher anlegen

Das Beschreiben der Rechenwege kann durch die das Anlegen eines Wortspeichers und  die Vorgabe von Sprachmustern und Satzbausteinen unterstützt werden (vgl. hierzu auch Förderschwerpunkt Sprache: Unterricht).

Zentrale Fachwörter / Möglicher Wortspeicher:

  • Rechenweg
  • Rechenschritt
  • Schrittweise
  • Hunderter, Zehner, Einer extra
  • Hilfsaufgabe
  • Addition
  • Subtraktion
  • Summe
  • Differenz
  • 1. Zahl
  • 2. Zahl
  • 1. Summand
  • 2. Summand
  • Minuend
  • Subtrahend
  • Hunderter
  • Zehner
  • Einer
  • Rechenstrich
  • Bogen
  • Startzahl
  • Ergebnis
  • addieren
  • subtrahieren
  • abziehen
  • zurückgehen
  • ergänzen
  • vorgehen
  • links (zurück)
  • rechts (vor)
  • zerlegen
     

Mögliche Sprachmuster / Satzbausteine:

  • Ich rechne schrittweise ...
  • Ich rechne eine Hilfsaufgabe ...
  • Ich ergänze ...
  • Ich starte bei / mit ...
  • Ich ziehe ... ab.
  • Ich addiere ... 

Möglichkeiten individueller Unterstützung

Markieren der Startzahl und Vorgabe von Richtungspfeilen

Eine Möglichkeit, insbesondere Kindern mit Wahrnehmungsschwierigkeiten die Orientierung am Rechenstrich zu erleichtern, besteht in der Markierung der Startzahl sowie im Einfügen von Richtungspfeilen.

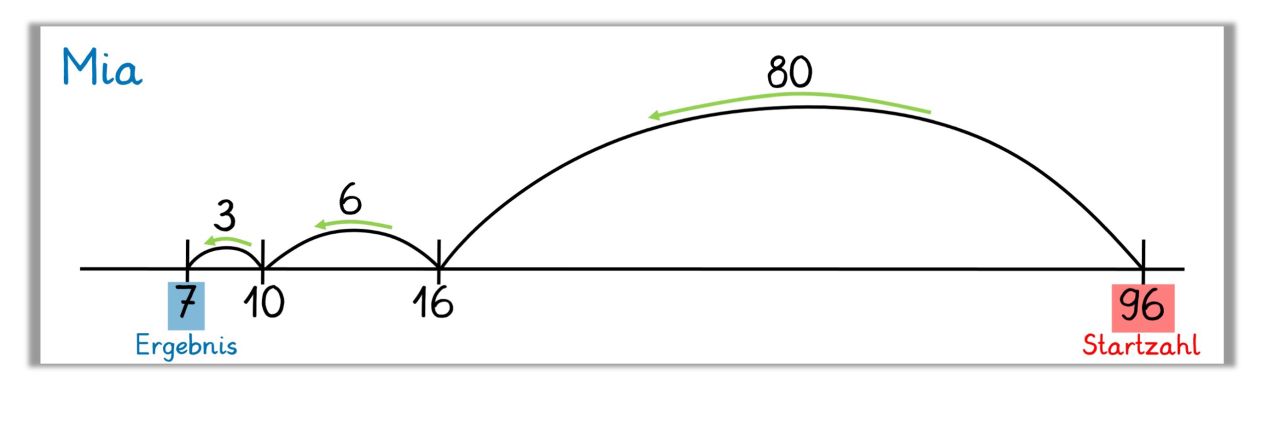
Karte: Rechenstrich mit den Zahlen 29, 37 und 67. Unter der Zahl 29 steht „Ergebnis“, unter der Zahl 67 „Startzahl“. Von rechts nach links 2 Bögen mit den Zahlen 30 und 4. Darüber kleine rote Pfeile.
Abbildung 21

Analog zur Basisaufgabe und zu den vertiefenden Aufgabenstellungen erhalten die Kinder Arbeitsblätter bzw. Karten mit Operationsdarstellungen am Rechenstrich, bei denen die Startzahl markiert ist und die "Leserichtung" der Bögen durch eingezeichnete Pfeile vorgegeben ist.

Wichtig ist auch in diesem Zusammenhang, dass im Vorfeld die Bedeutung der markierten Zahlen und der Richtungspfeile geklärt wird.

Kurz-URL: https://pikas-mi.dzlm.de/node/618

QR-Code downloaden