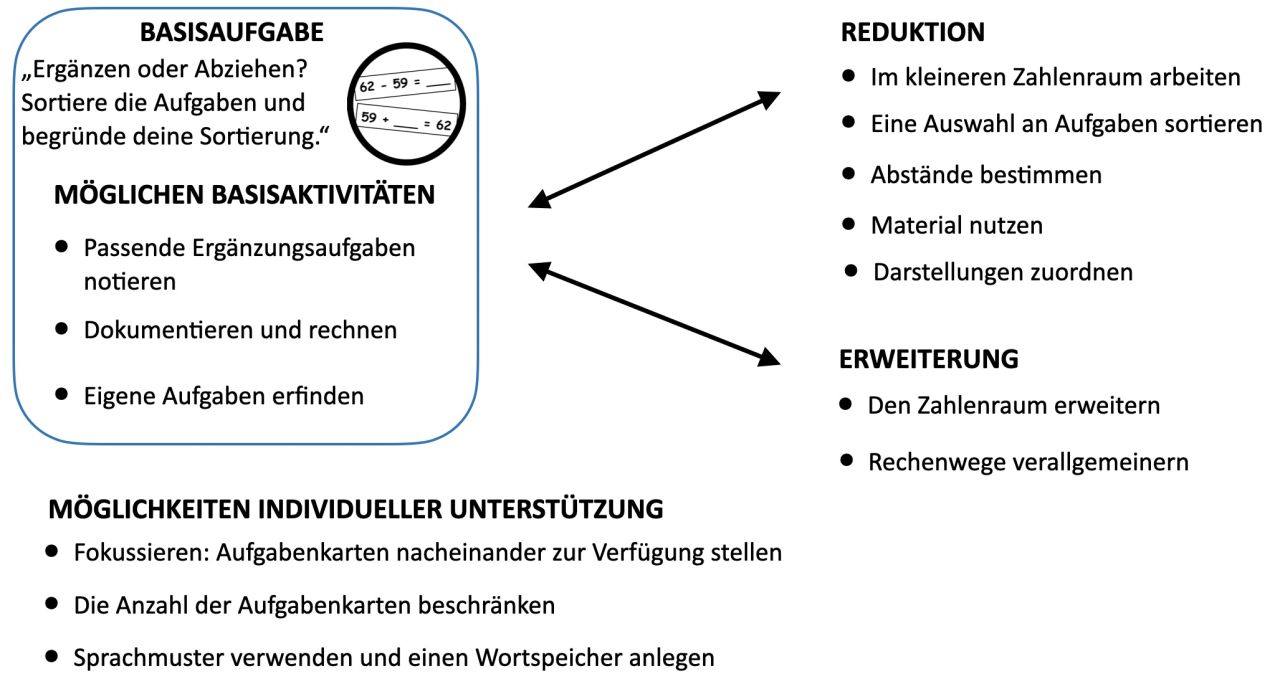
 Abb. 1: Übersicht_Aufgabenstellung kompakt "Ergänzen oder Abziehen"
Abb. 1: Übersicht_Aufgabenstellung kompakt "Ergänzen oder Abziehen"
Download Übersicht
Grundlegendes
Eine wichtige Zielsetzung im Inhaltsbereich Zahlenrechnen besteht darin, dass die Kinder Zahlbeziehungen und Rechengesetze für vorteilhaftes Rechnen nutzen und sich darüber bewusst werden, bei welchen Aufgaben der Einsatz bestimmter Strategien und Vorgehensweisen besonders effektiv und geschickt ist (vgl. Lehrplan NRW, S. 62).
Dieses fällt jedoch nicht nur Kindern mit Lernschwierigkeiten oft schwer. Bei der Wahl der Rechenstrategie zeigen Schülerinnen und Schüler im Unterricht oft ein recht stabiles Vorgehen und neigen dazu, eher vertraute „Rechen-Wege“ zu gehen.
In einer Untersuchung von Selter (2000), in der Schülerinnen und Schüler des 3. Schuljahres Additions- und Subtraktionsaufgaben rechnen sollten, zeigte sich beispielsweise, dass die Kinder, die die Aufgaben mit einer halbschriftlichen Strategie lösten, "in der Regel sämtliche Aufgaben gemäß einer der Hauptstrategien, also zum Beispiel jede Aufgabe (und dann auch 701 - 698) nach der Strategie ’Stellen extra’" (Selter 2000, S. 250) rechneten.
Von grundlegender Bedeutung ist deshalb, im Unterricht immer wieder Zusammenhänge und Beziehungen zwischen Zahlen und Aufgaben aufzugreifen, den "Zahlenblick" zu schulen und die Frage nach einer sinnvollen Rechenstrategie in den Mittelpunkt des Unterrichts zu stellen. Denn auch für Kinder mit Lernschwierigkeiten gilt:
„Je mehr aber Zahlbeziehungen und Muster generell im Unterricht thematisiert werden, desto wahrscheinlicher kann sich Verständnis dafür einstellen und für den flexiblen Einsatz von verschiedenen Strategien genutzt werden“ (Scherer & Moser Opitz 2010, S. 154).
Subtraktionsaufgaben durch Ergänzen lösen
Im Fokus der folgenden Aufgabenstellung kompakt steht das Ergänzen als Möglichkeit, Subtraktionsaufgaben vorteilhaft zu lösen.
Während die Mehrzahl der Hauptstrategien der halbschriftlichen Subtraktion (wie beispielsweise Stellenwerte extra oder Schrittweise) auf der Grundvorstellung des Abziehens basiert, betont die Strategie des Ergänzens stärker den Zusammenhang sowie die enge Beziehung zwischen Addition und Subtraktion und zeigt auf, dass Differenzen auch additiv ermittelt werden können. Ausführliche Hintergrundinformationen hierzu finden sie in der Rubrik Inhalte unter Zahlenrechnen: Hintergrund sowie unter Operationsvorstellungen: Hintergrund.
Die Fähigkeit, eine Subtraktionsaufgabe additiv zu deuten bzw. zu interpretieren ist eine der Grundlagen eines umfassenden Operationsverständnisses (vgl.: Inhalte: Operationsvorstellungen) und bietet die Möglichkeit, insbesondere Subtraktionsaufgaben, bei denen Minuend und Subtrahend nahe beieinander liegen, einfacher und vorteilhafter zu lösen.
Vorteilhaft rechnen
Wie nun gemeinsam mit allen Kindern die Frage nach vorteilhaften und geschickten Rechenwegen in den Blick genommen werden kann, möchten wir im Folgenden am Beispiel einer Aufgabenstellung aufzeigen, bei der es um das Sortieren von Aufgaben und die Entscheidung für einen Rechenweg geht.
Das Ergänzen sollte bereits im Vorfeld hinreichend thematisiert worden sein.
Dabei sind wichtige Aspekte:
-
Aufbau von Grundvorstellungen: Abziehen und Ergänzen im Sachkontext. Kennenlernen des „Ergänzens“ als eine Möglichkeit, Subtraktionsaufgaben zu lösen.
-
Ergänzungsaufgaben bilden („Wie heißt die zugehörige Ergänzungsaufgabe?“ / „Löse durch Ergänzen.“) und Darstellungsoptionen erkunden (am Punktefeld, Rechenstrich, …).
-
Handlungen und Darstellungen verbalisieren: „Ich ergänze …“.
-
Aufgaben und Umkehraufgaben (sog. Aufgabenfamilien) kennen (z. B. 23 + 14 = 37,
14 + 23 = 37, 37 - 14 = 23, 37 - 23 = 14).
-
Elementares Ergänzen bereits in den Jahrgangsstufen 1 und 2: 7 + _ = 10, 93 + _ = 100.
In der Jahrgangsstufe 3: Ergänzen bis 1000 am Tausenderfeld (Zahl legen, nennen und bis 1000 ergänzen).
-
Ergänzen zum Zehner und Abziehen zum Zehner als Kernaufgaben kennen.
Basisaufgabe
„Ergänzen oder Abziehen? Sortiere die Aufgaben und begründe deine Sortierung.“
Material: Sortiertafel, Aufgabenkarten
Die Schülerinnen und Schüler erhalten verschiedene Karten mit Subtraktionsaufgaben und eine Sortiertafel:
„Ergänzen oder Abziehen? Sortiere die Aufgaben und begründe deine Sortierung.“
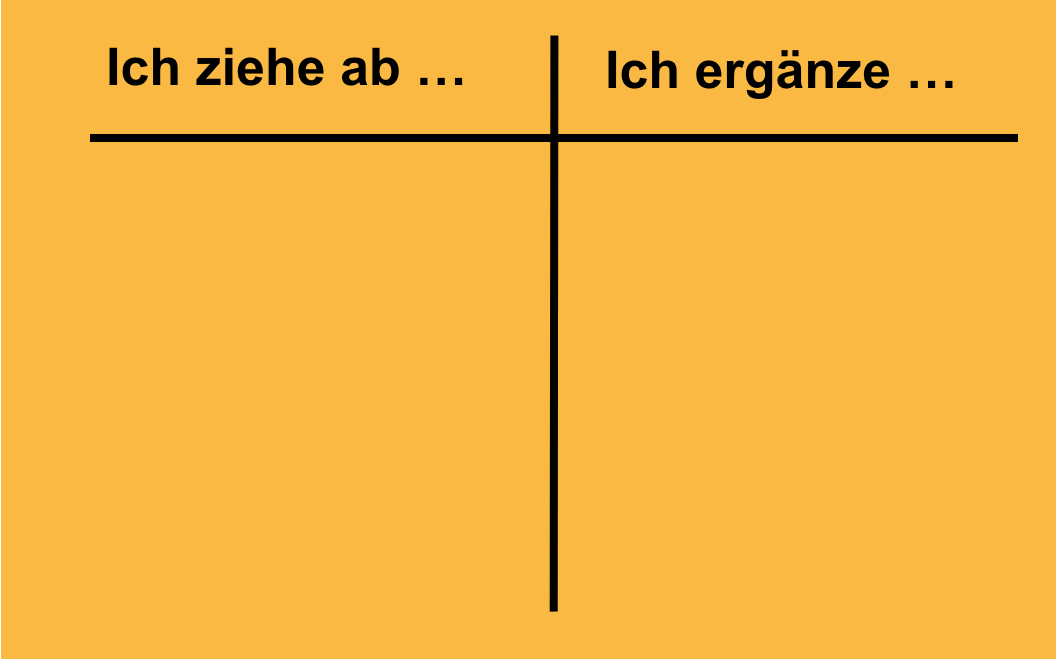 Abb. 2
Abb. 2
Die Aufgabe kann in Einzel- oder Partnerarbeit durchgeführt werden.
Arbeiten immer zwei Kinder gemeinsam, müssen sie sich in Bezug auf die Einsortierung der einzelnen Aufgaben einigen. Hierdurch werden sie ggfs. bereits während der Sortierphase angeregt, ihre Ideen bzgl. einer möglichen Einsortierung zu verbalisieren und gegenüber dem jeweiligen Partnerkind zu begründen.
In Bezug auf die Frage, welche Aufgaben den Kindern zur Verfügung gestellt werden sollten, gibt es verschiedene Kriterien.
Wichtig ist zum einen, dass bei einem Teil der Aufgaben die Strategie des Ergänzens naheliegt. Zum anderen sollte die Auswahl der Aufgaben allen Kindern die Gelegenheit eröffnen, sich in einer anschließenden gemeinsamen Reflexionsphase zu beteiligen.
Damit die Kinder die Übersicht behalten, kann es sinnvoll sein, zunächst nur eine begrenzte Anzahl an Karten zur Verfügung zu stellen.
Durchführung im 2. Schuljahr:
Die Schülerinnen und Schüler erhalten Aufgaben aus dem Zahlenraum bis 100 (darunter sind auch Aufgaben aus dem Zahlenraum bis 20).
Beispielhafte Aufgabenauswahl:
 Abb. 3
Abb. 3
Durchführung im 3. Schuljahr:
Die Schülerinnen und Schüler erhalten Aufgaben aus dem Zahlenraum bis 1000 (darunter sind auch Aufgaben aus dem Zahlenraum bis 100).
Beispielhafte Aufgabenauswahl:
 Abb. 4
Abb. 4
Zuordnungen begründen
Nach der Sortierung der Aufgaben werden die Kinder angeregt, ausgewählte Zuordnungen zu begründen. Die Notation der Begründungen kann sowohl in Einzelarbeit, aber auch in Partnerarbeit durchgeführt werden.
Einzelarbeit:
Die Schülerin bzw. der Schüler wählt aus jeder der beiden Kategorien eine der Aufgaben aus und notiert eine Begründung.
Partnerarbeit:
Wurde die Sortierung der Aufgaben noch in Einzelarbeit durchgeführt, können die Kinder jetzt ihre Sortierung mit der Sortierung ihres Partnerkindes vergleichen. Anschließend wählen sie gemeinsam eine Aufgabe aus, die gleich einsortiert wurde, und notieren eine Begründung. Haben die Kinder bereits bei der Sortierung der Aufgaben gemeinsam gearbeitet, wählen sie nun aus jeder der beiden Kategorien eine der von ihnen gelegten Aufgaben und notieren ihre Begründung.
 Abb. 5
Abb. 5
Die Anforderung, einzelne ausgesuchte Sortierungen zu begründen, kann die Kinder herausfordern, sich mit der Frage auseinanderzusetzen, wann Ergänzen eine sinnvolle Strategie darstellt.
Wichtig:
Grundsätzlich gilt, dass jede der Aufgaben sowohl durch Ergänzen als auch durch Abziehen gelöst werden kann und dass es nicht zwangsläufig zu einer Aufgabe nur eine vorteilhafte Strategie gibt.
Oft gibt es mehrere sinnvolle Wege, so dass es in Bezug auf die Sortierung der Aufgaben auf keinen Fall von einer "richtigen" bzw. "falschen" Sortierung gesprochen werden kann bzw. darf.
Gleichwohl liegt es bei einigen der vorgegebenen Aufgaben nahe, das Ergebnis über Ergänzen zu bestimmen. Beispielsweise dann, wenn Minuend und Subtrahend nah beieinander liegen.
Eine mögliche Begründung in Bezug auf die Aufgabe 801 - 799 wäre deshalb beispielsweise:
"Ergänzen geht schneller / ist einfacher, weil die beiden Zahlen nah beieinander liegen."
Aber auch das "Vereinfachen" stellt in Bezug auf diese Aufgabe eine sinnvolle Strategie dar. Vorstellbar ist, dass die Kinder die Aufgabe unter "Ich ziehe ab …" einsortieren bzw. notieren:
"Statt 801 - 799 rechne ich einfach 802 - 800. Das Ergebnis bleibt gleich."
Neben möglichen (wünschenswerten) Argumentationen auf der Grundlage der jeweiligen Zahlbeziehungen, sind auch Begründungen denkbar, die auf der Einschätzung / Grundlage der eigenen Fähigkeiten und Vorlieben getroffen werden wie beispielsweise:
-
Ich finde Ergänzen einfacher, das kann ich im Kopf …
-
Ich rechne lieber plus als minus deshalb ergänze ich …
-
Wenn ich plus rechne, mache ich weniger Fehler …
-
Abziehen geht schneller, das kann ich im Kopf rechnen ...
-
Ich ziehe lieber ab, dann muss ich die Aufgabe nicht umstellen …
Gemeinsam reflektieren
Wichtig ist, dass die Kinder im Anschluss an die Bearbeitung der Aufgabe noch einmal in einen Austausch gehen und die Gelegenheit erhalten, in einer Reflexionsphase
-
ihre Sortierungen vorzustellen,
-
die Sortierungen der anderen Kinder mit der eigenen Sortierung zu vergleichen,
-
Gemeinsamkeiten und Unterschiede festzustellen,
-
die Zahlbeziehungen zu beschreiben,
-
ihre Sortierung und die Entscheidung für eine der Kategorien zu verbalisieren und zu begründen,
-
die Begründungen der anderen Kinder nachzuvollziehen.
Hierdurch kann den Blick auf die eigenen Sortierungen erweitert und verändert werden:
"Wo würdest du die Aufgabe jetzt einsortieren? Erkläre!"
Basisaktivität
Passende Ergänzungsaufgaben notieren
Material: Sortiertafel, leere Aufgabenkarten, AB
Die Aufgaben, die in der Kategorie „Ich ergänze …“ eingeordnet wurden, werden von den Kindern als Ergänzungsaufgabe (Plusaufgabe / Platzhalteraufgabe) notiert.
"Schreibe als Ergänzungsaufgabe."
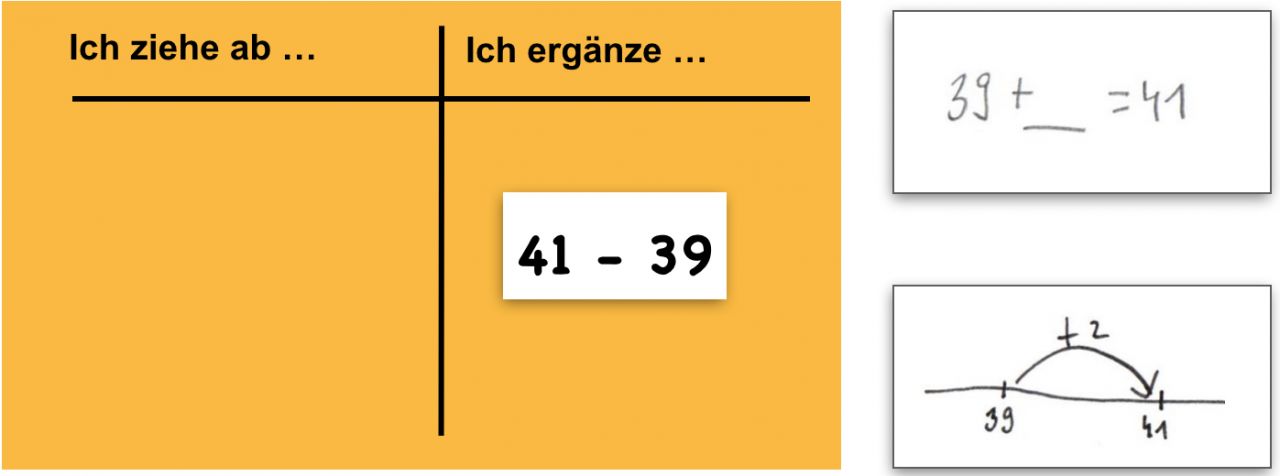 Abb. 6
Abb. 6
Basisaktivität
Dokumentieren und rechnen
Material: Aufgabenkarten, AB
Die Kinder rechnen die Aufgaben, bei denen sie die Sortierung begründet haben, auf ihrem Weg und entsprechend der jeweiligen Sortierung (Abziehen oder Ergänzen). Dabei dokumentieren sie ihre Vorgehensweise.
Die Kinder können wählen, ob sie ihre Rechnung symbolisch notieren, am Rechenstrich darstellen, zeichnen oder mit Worten beschreiben möchten. In Abhängigkeit von den jeweiligen Lernvoraussetzungen kann es sinnvoll sein, einzelne Kinder durch den Einsatz von Material bei der Lösung der Aufgabe zu unterstützen (vgl. hierzu Reduktion: Rechnen und dokumentieren: Material nutzen).
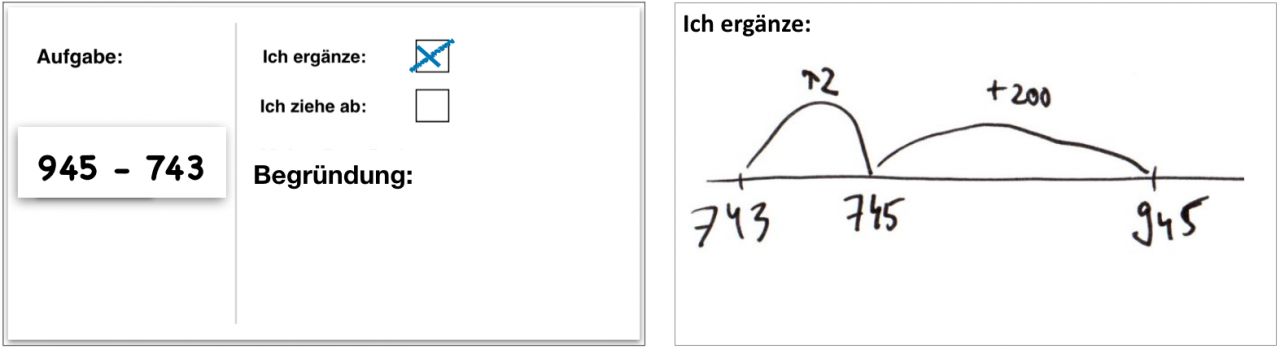 Abb. 7
Abb. 7
 Abb. 8
Abb. 8
Basisaktivität
Eigene Aufgaben erfinden
Material: Sortiertafel, leere Aufgabenkarten
Vertiefend können die Kinder eigene Aufgaben notieren, die sie entweder durch Ergänzen oder Abziehen berechnen würden:
„Erfinde Aufgaben und sortiere sie ein.“
Analog zur Basisaufgabe können auch hier die Kinder angeregt werden, ihre Sortierung zu begründen.
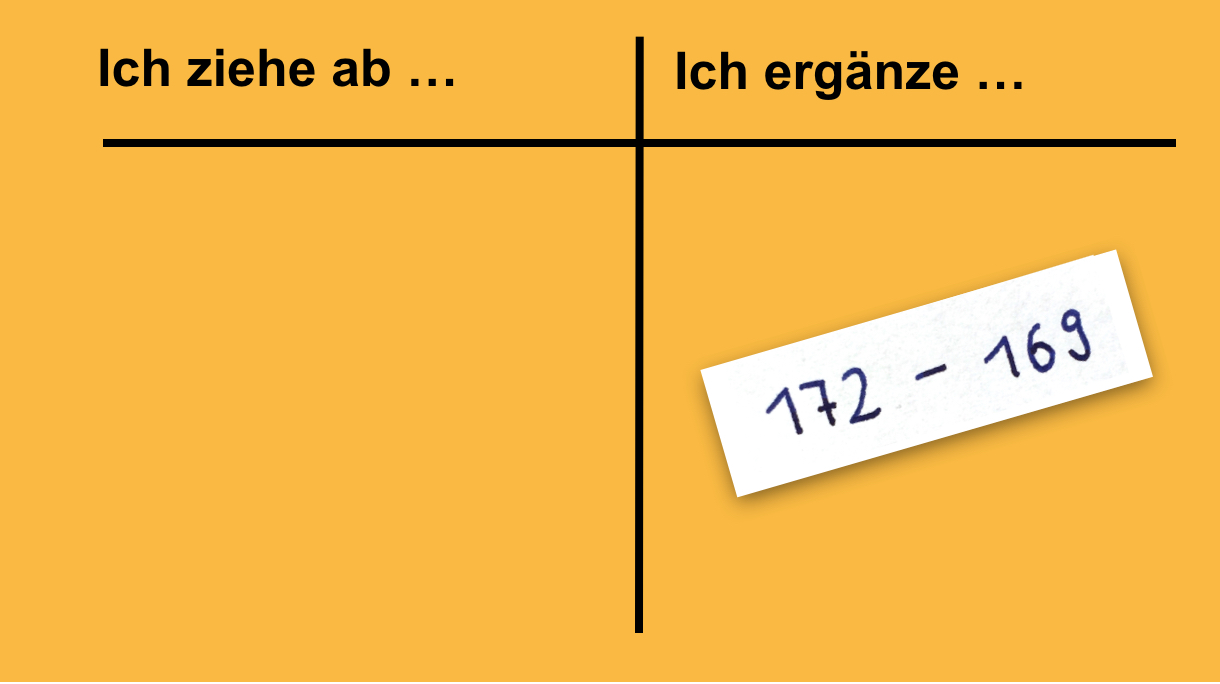 Abb. 9
Abb. 9
Reduktion
Im kleineren Zahlenraum arbeiten
Material: Sortiertafel, Aufgabenkarten, AB
In Abhängigkeit von den individuellen Lernvoraussetzungen kann für einzelne Schülerinnen und Schüler eine Reduktion der inhaltlichen Anforderungen erreicht werden, indem der Fokus auf Aufgaben aus einem Zahlraum gelegt wird, in dem sich die Kinder sicher bewegen (beispielsweise auf Aufgaben aus dem Zahlenraum bis 20 oder 100).
Dabei muss bei der Wahl der Aufgaben darauf geachtet werden, dass zumindest ein Teil der Aufgaben in Analogie zu Aufgaben der Basisaufgabe steht.
Mögliche Aufgaben aus dem Zahlenraum bis 20 (Vergleiche hierzu die Aufgaben der Basisaufgabe aus dem Zahlenraum bis 100):
 Abb. 10
Abb. 10
Werden für die Basisaufgabe Aufgaben aus dem Zahlrenraum bis 1000 gewählt, können für Kinder mit Lernschwierigkeiten analoge Aufgaben aus dem Zahlenraum bis 100 (oder aus dem Zahlenraum bis 20) ausgewählt werden. Eine Auswahl von möglichen Aufgaben für den Zahlenraum bis 100 finden Sie bei der Darstellung der Basisaufgabe.
Reduktion
Eine Auswahl an Aufgaben sortieren
Material: Sortiertafel, Aufgabenkarten
Eine weitere Möglichkeit einer inhaltlichen Reduktion:
Aus den für die Bearbeitung der Basisaufgabe vorgegebenen Aufgaben werden im Vorfeld von der Lehrkraft spezifische Aufgaben ausgewählt, die dann von dem Kinder sortiert werden.
So kann beispielsweise der Fokus auf Aufgaben gelegt werden, bei denen der Zehner nicht unterschritten wird (vgl. zur Aufgabenauswahl die Basisaufgabe):
 Abb. 11
Abb. 11
Reduktion
Abstände bestimmen
Material: Aufgabenkarten, AB
Das Begründen der Einordnung bzw. Sortierung der Aufgaben ist ein wesentlicher Bestandteil der Basisaufgabe („Sortiere die Aufgaben und begründe deine Sortierung“). Wünschenswert ist hierbei, dass die Kinder auf der Grundlage der Zahlbeziehungen argumentieren und beispielsweise erkennen, dass sich das Ergänzen als Möglichkeit, Subtraktionsaufgaben zu lösen, insbesondere dann anbietet, wenn Minuend und Subtrahend nah beieinander liegen.
Um den Fokus auf auf diese Zahlbeziehungen (auf die Beziehung zwischen Minuend und Subtrahend) zu legen und Kinder gezielt anzuregen, die Abstände zwischen Zahlen in den Blick zu nehmen, erhalten die Kinder Zahlenpaare, die jeweils aus Minuend und Subtrahend der vorgegebenen Aufgaben (vgl. hierzu die Basisaufgabe) bestehen:
"Lege die Zahlen an den Rechenstrich. Bei welchen Zahlenpaaren kannst du sofort (schnell?) erkennen, wie groß der Abstand ist?"
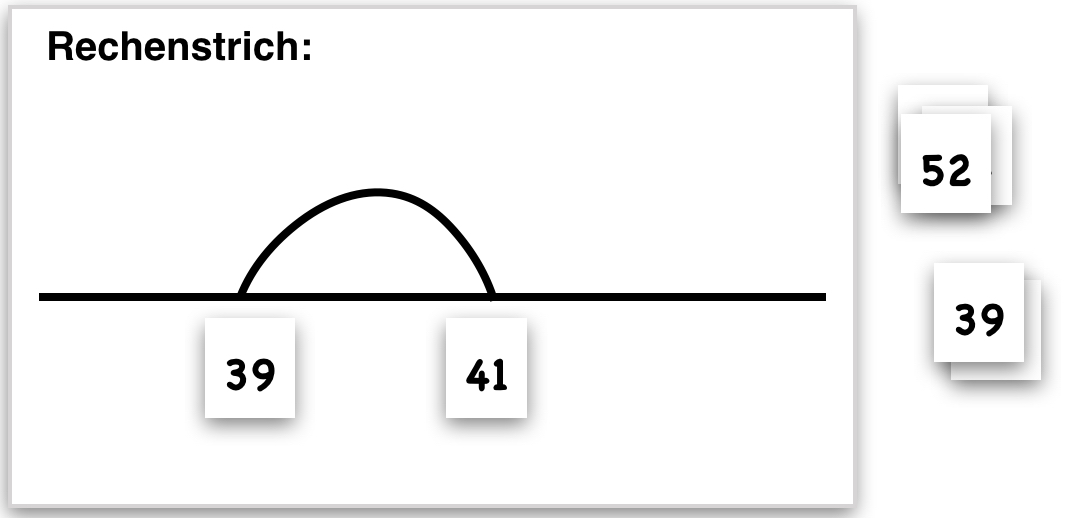 Abb. 12
Abb. 12
Abschließend kann gemeinsam überlegt werden, was die Zahlenpaare auf der Sortiertafel von den anderen, aussortierten Zahlenpaaren unterscheidet:
"Warum kannst du das bei diesen Zahlenpaaren sofort (schnell) erkennen?"
Reduktion
Material nutzen
Material: Aufgabenkarten / Dienes-Material (Mehrystemblöcke) / Tablet / evtl. Eingabestift
In Abhängigkeit von den jeweiligen Lernvoraussetzungen kann es sinnvoll sein, einzelne Kinder durch den Einsatz von Material bei der Lösung der Aufgabe zu unterstützen. Das eingesetzte Material sollte den Kindern vertraut sein.
Die Dokumentation kann beispielsweise über eine Abfolge von Fotos erfolgen. Hier bietet es sich an, dass die Kinder das Material legen, jeden Schritt mit dem tablet fotografieren, anschließend auf den Fotos die einzelnen Schritte markieren und notieren, wie viele Hunderter, Zehner und Einer sie ergänzt bzw. abgezogen haben (mit dem Eingabestift). Diese Form der Dokumentation fordert die Kinder heraus, jeden einzelnen Schritt bewusst in den Blick zu nehmen. Sie kann dabei helfen, die Übersicht zu behalten, da die Kinder auch während des Prozesses immer wieder „zurückschauen“ können. (Wie viele Hunderter, Zehner, Einer lagen zu Beginn auf dem Tisch? Was habe ich hinzugelegt bzw. weggenommen? …)
Beispiel
Schritt 1: Mit Material (Mehrsystemblöcke) wird die Zahl 743 gelegt:
Schritt 2: Anschließend wird ergänzt: „Wie viele fehlen noch bis 945?“
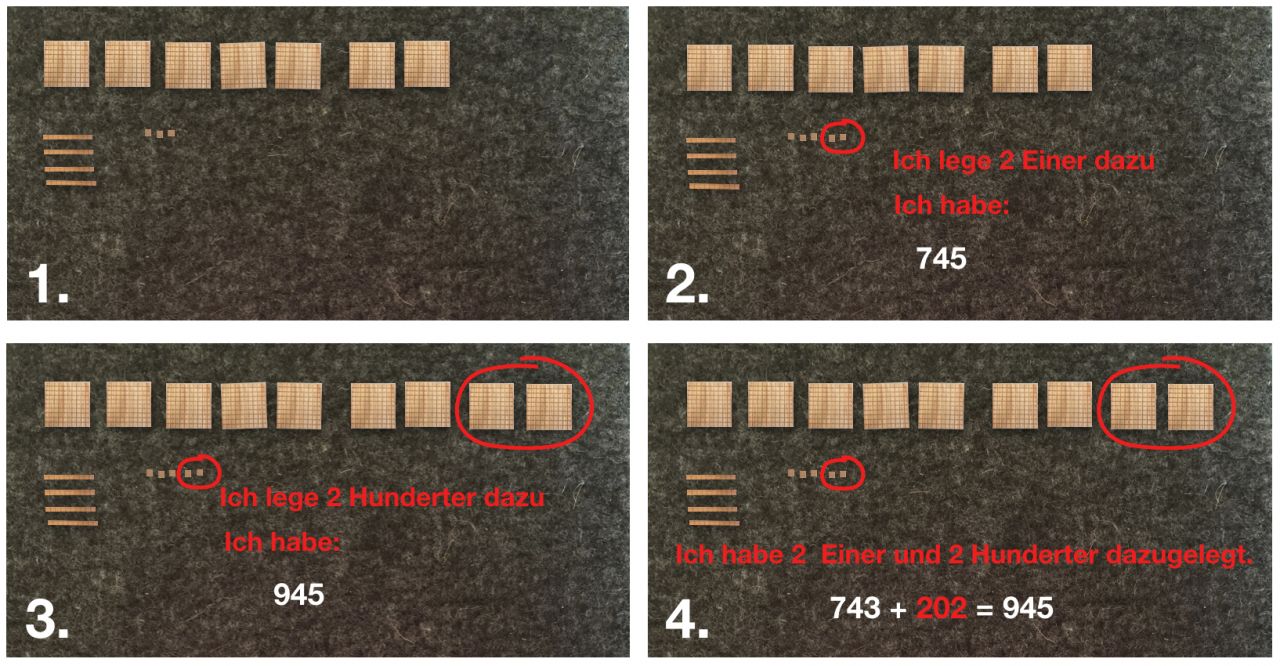 Abb. 13
Abb. 13
Reduktion
Darstellungen zuordnen
Material: Sortiertafel, Aufgabenkarten
Eine Schwierigkeit in Bezug auf das Ergänzen als Möglichkeit, Subtraktionsaufgaben zu lösen, besteht in der Umdeutung und Notation der Aufgabe als Ergänzungsaufgabe. Dieses ist aber eine Voraussetzung, um begründet entscheiden zu können, ob Ergänzen (bezogen auf eine konkrete Aufgabe) eine vorteilhafte Strategie darstellt.
Alternativ zur möglichen Basisaktivität „Passende Ergänzungsaufgaben notieren“ können passende Ergänzungsdarstellungen angeboten werden, die dann von den Kindern zugeordnet werden. Hierdurch wird die Komplexität der Basisaktivität verringert, gleichwohl werden die Kinder herausgefordert, sich mit den Ergänzungsdarstellungen auseinanderzusetzen, Aufgaben zu vergleichen und zu überlegen, welche Aufgaben zueinander passen.
Mögliche Aufgabenkarten und passende Ergänzungsdarstellungen:
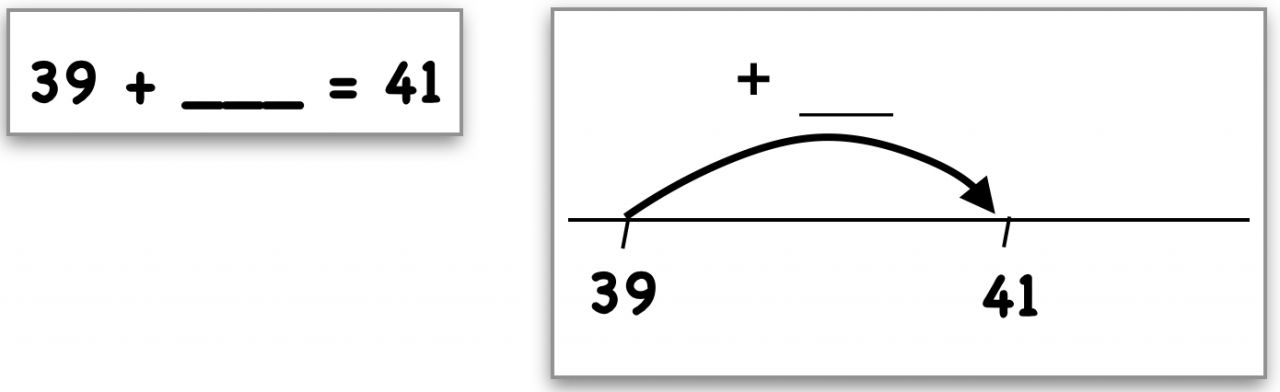 Abb. 14
Abb. 14
Bei der Wahl der Ergänzungsdarstellungen sollten die Lernvoraussetzungen der Kinder berücksichtigt werden. Wichtig ist, eine den Kindern vertrautet Darstellung anzubieten:
"Finde die passende Ergänzungsdarstellung."
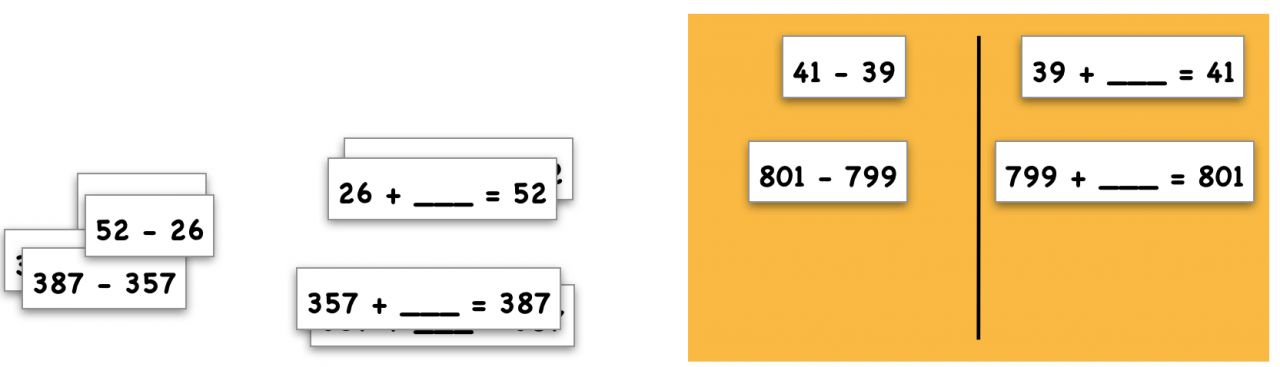 Abb. 15
Abb. 15
Erweiterung
Den Zahlenraum erweitern
Material: Sortiertafel, Aufgabenkarten
Um die Anforderunge zu erhöhen, können die Kinder auch Aufgaben erhalten, die über den Tausenderraum hinausgehen.
Auch hier muss bei der Auswahl der Aufgaben darauf geachtet werden, dass zumindest ein Teil der Aufgaben in Analogie zu den Aufgaben steht, die von den anderen Kindern in der Klasse sortiert werden (vgl. hierzu die Aufgaben der Basisaufgabe).
Mögliche Aufgaben (Beispiele):
 Abb. 16
Abb. 16
Erweiterung
Rechenwege verallgemeinern
Material: Sortiertafel, Aufgabenkarten
Leistungsstarke Kinder können zudem herausgefordert werden, auf einem Plakat, bzw. mittels einer am Computer / Tablet erstellten Präsentation etc. noch einmal das Ergänzen darzustellen und dabei nach Verallgemeinerungen zu suchen:
Sinnvoll kann es hier auch sein, ein weiteres Verfahren in die Überlegungen mit einzubeziehen (wie z. B. das Vereinfachen).
-
Geht Ergänzen immer? Geht Vereinfachen immer?
-
Bei welchen Aufgaben stellt das Ergänzen einen vorteilhaften Rechenweg dar? Bei welchen das Vereinfachen?
-
Vergleiche: Bei welchen Aufgaben sind beide Wege vorteilhaft? Wo gibt es Unterschiede?
Möglichkeiten individueller Unterstützung
Fokussieren: Aufgabenkarten nacheinander zur Verfügung stellen
Für einzelne Kinder kann es entlastend sein, wenn sie nicht alle Aufgabenkarten gleichzeitig erhalten. Denkbar ist beispielsweise, dass die Kinder zunächst 5 Karten erhalten und erst nach deren Sortierung die nächsten 5 oder dass sie aus einer Box immer erst dann eine neue Karte nehmen, wenn sie die vorhergehende einsortiert haben.
Möglichkeiten individueller Unterstützung
Die Anzahl der Aufgabenkarten beschränken
Überlegt werden kann auch, die Anzahl der Aufgabenkarten insgesamt zu reduzieren. D.h. das Kind erhält beispielsweise statt 10 Aufgabenkarten nur 5.
Möglichkeiten individueller Unterstützung
Sprachmuster verwenden und einen Wortspeicher anlegen
Das Beschreiben der Rechenwege kann durch das Anlegen eines Wortspeichers und die Vorgabe von Sprachmustern und Satzbausteinen unterstützt werden (vgl. hierzu auch Förderschwerpunkte: Sprache: Unterricht).
Zentrale Fachwörter / Möglicher Wortspeicher:
-
Rechenweg
-
Rechenschritt
-
Ergänzen
-
Addition
-
Subtraktion
-
Ergebnis
-
Summe
-
Unterschied
-
Differenz
-
1. Zahl
-
2. Zahl
-
1. Summand
-
2. Summand
-
Minuend
-
Subtrahend
-
Hunderter
-
Zehner
-
Einer
-
Rechenstrich
-
Bogen
-
Startzahl
-
addieren
-
subtrahieren
-
abziehen
-
zurückgehen
-
ergänzen
-
vorgehen
-
links (zurück)
-
rechts (vor)
Mögliche Sprachmuster / Satzbausteine:
-
Ich ziehe ... ab
-
Ich ergänze ...
-
Ich starte bei / mit ...
-
Ich addiere ...