Das "Zahlenrechnen" gehört zu den Schwerpunkten des Bereiches "Zahlen und Operationen" im Lehrplan für den Mathematikunterricht an Grundschulen (vgl. MSW NRW, 2008). Gekennzeichnet ist es durch das Operieren mit Zahlganzheiten: Schwierigere und komplexere Aufgaben werden durch leichtere Teilaufgaben - unter Verwendung von Zahlbeziehungen, Rechengesetzen und Rechenvorteilen - gelöst.
Dabei können zwei grundlegende Varianten unterschieden werden:
1. Kopfrechnen
Kinder rechnen mit Zahlen ausschließlich mündlich, d.h. Aufgaben werden ohne zusätzliche Notationen gelöst, Rechnungen und Rechenschritte werden "im Kopf" durchgeführt.
Abgegrenzt und unterschieden werden muss diese Variante des Zahlenrechnens vom "schnellen Kopfrechnen" (vgl. MSW NRW, 2008, S. 62), bei dem es um die gedächtnismäßige und automatisierte Wiedergabe von Aufgaben und Ergebnissen geht.
Abb. 1
Beispiel 1 (ZR bis 100):
51– 16
Leni: "Ich rechne zuerst einundfünfig minus zehn gleich einundvierzig. Von einundvierzig ziehe ich jetzt noch sechs ab. Das Ergebnis der Aufgabe ist fünfunddreißig."
Sibel: "einundfünfzig, einundvierzig, vierzig, fünfunddreißig. Das Ergebnis ist fünfunddreißig."
Beispiel 2 (ZR bis 1000):
568 – 262
Tobi: "Ich ziehe von fünfhundertachtundsechzig zuerst zweihundert ab. Das ergibt dreihundertachtundsechzig. Dann ziehe ich noch zweiundsechzig ab. Das Ergebnis der Aufgabe ist dreihundertsechs."
Hamza: "fünfhundertachtundsechzig minus zweihundert ... dreihundertachtundsechzig, dreihundertacht, das Ergebnis ist dann dreihundertsechs."
Abb. 2
2. Halbschriftliches Rechnen
Notieren Kinder beim Rechnen einzelne Rechenschritte oder Zwischenlösungen, spricht man von "halbschriftlichem" Rechnen oder auch von einem "gestützten" Kopfrechnen (vgl. Radatz et al. 1999).
Dabei gilt für alle Rechenoperationen, dass weder die Vorgehensweise noch die Notation und Darstellung der Rechenschritte bzw. des Rechenweges festgelegt oder vorgeschrieben ist.
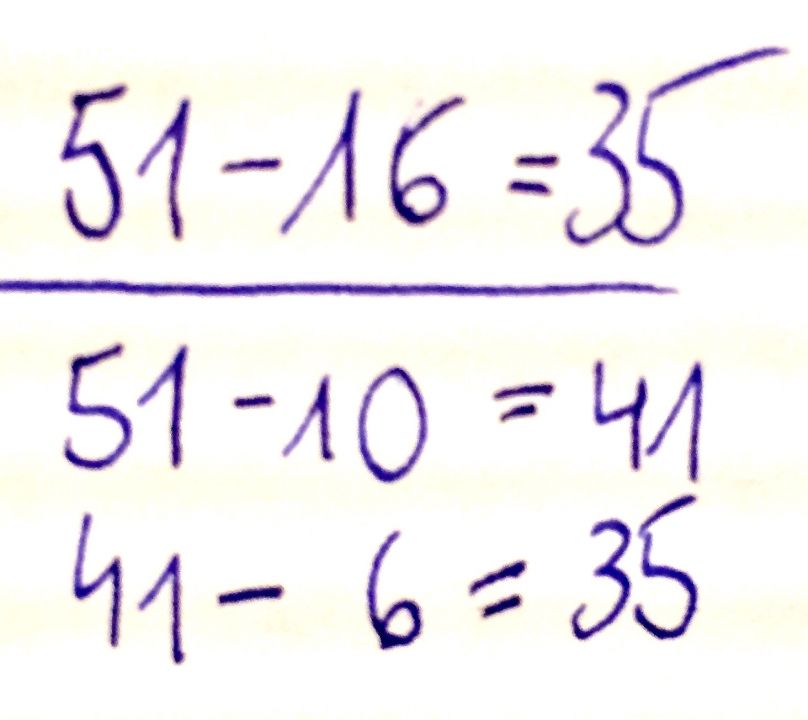Abb. 3
Beispiel 2 (ZR bis 1000):
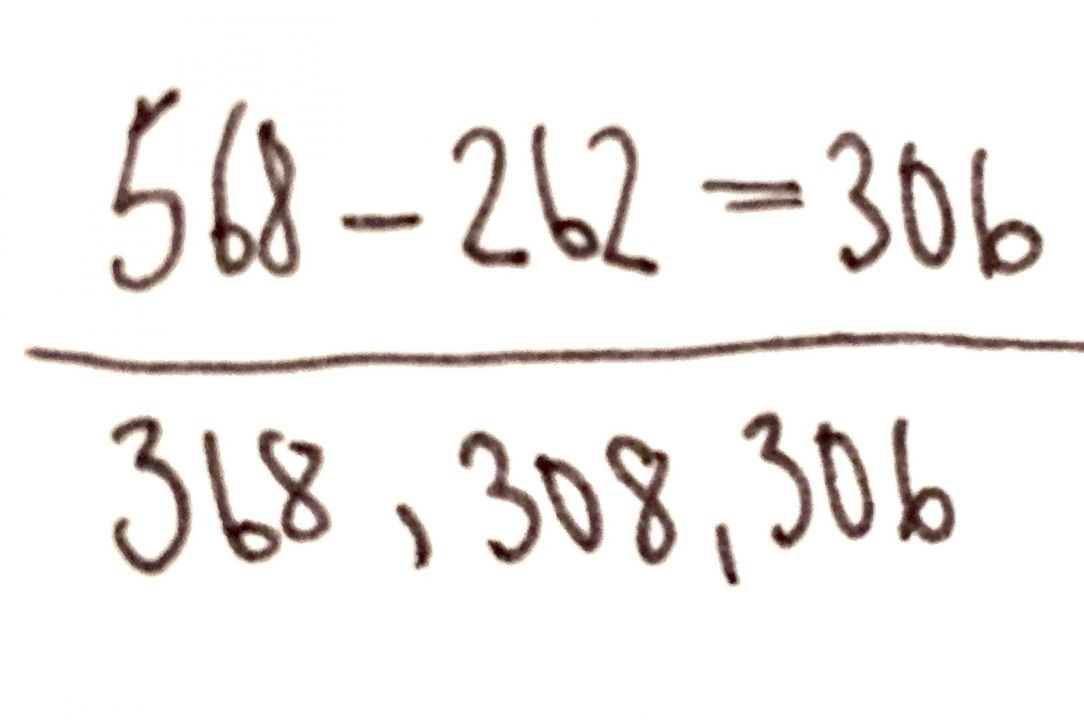Abb. 4
Das Rechnen mit Zahlen bzw. Zahlganzheiten fördert und fordert individuelle Zugänge sowie die Entwicklung eigener Vorgehensweisen bei der Bearbeitung von Aufgaben in allen vier Grundrechenarten.
Doch wie können Kinder hierbei unterstützt werden? Und was muss insbesondere bei der Arbeit mit Kindern beachtet werden, die Lernschwierigkeiten haben?
Am Beispiel der Subtraktion wird diesen Fragen im Folgenden ausführlich nachgegangen.
In einem ersten Teilmodul wird zunächst die Bedeutung, die das Zahlenrechnen im und für den Mathematikunterricht der Grundschule hat, in den Blick genommen. Erörtert werden zudem die Besonderheiten des Zahlenrechnens und die für die Subtraktion (ideal-)typischen Rechenstrategien. Einen Schwerpunkt stellt hier die Frage nach den Möglichkeiten der Darstellung und Veranschaulichung dar.
Im Mittelpunkt des zweiten Teilmoduls steht dann die Frage, wie alle Kinder – unabhängig von ihren jeweiligen Lernvoraussetzungen – sowohl in der Schuleingangsphase als auch später im 3. und 4. Schuljahr bei der Entwicklung tragfähiger Rechenwege unterstützt werden können.
