Aufgabenstellungen Kompakt "Teilen in gleich große Teile"
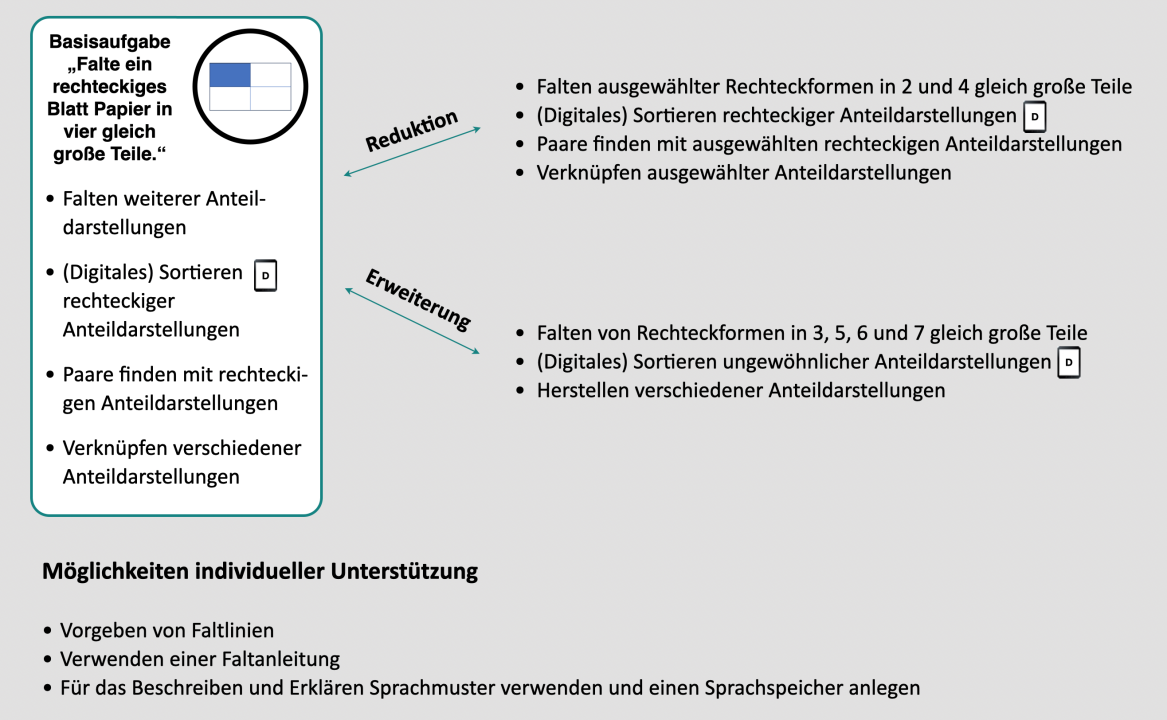
Basisaufgabe
„Falte ein rechteckiges Papier immer in vier gleich große Teile. Finde unterschiedliche Möglichkeiten und färbe immer einen Teil. Wie kannst du überprüfen, ob die Teile gleich groß sind?“
Material: Papierrechtecke gleicher Größe, Stifte
Im Rahmen dieser Basisaufgabe setzen sich die Lernenden einführend mit der Grundvorstellung Bruch als Anteil auseinander. Im Fokus steht dabei die Erkenntnis, dass ein Ganzes immer in gleich große Teile unterteilt werden muss. Die Aktivitäten sind auf die Auseinandersetzung mit den Stammbrüchen (Zähler = 1) reduziert. Eine Erweiterung und Vertiefung erfolgen in der Aufgabenstellung kompakt Teil-Ganzes-Anteil.
Zuerst erhalten die Lernenden mehrere Seiten rechteckiges Papier und finden in Zweiergruppen verschiedene Möglichkeiten, die Blätter in vier gleich große Teile zu falten. Jeweils einen der vier Teile färben die Lernenden immer ein.
Anschließend kommen sie in Gruppen zusammen, vergleichen ihre Faltungen miteinander und sortieren doppelte aus.
Mögliche Impulse für die Gruppenarbeit:
- Auf diesem Blatt sehen die Dreiecke unterschiedlich aus. Wie kannst du überprüfen, ob sie trotzdem gleich groß sind?
- Jedes Blatt wurde in vier gleich große Teile geteilt. Es sind unterschiedliche Rechtecke und Dreiecke entstanden. Was kannst du über die Größe der unterschiedlichen Teile sagen? Begründe deine Antwort.
Abschließend werden die Ergebnisse zusammengetragen und diskutiert, welche Faltungen unterschieden werden können und woran der gleiche Flächeninhalt der einzelnen Teile erkannt werden kann.

Mögliche Reflexionsfragen für die Abschlussphase:
- Warum muss das blaue Rechteck gleich groß wie die drei anderen Rechtecke des Blattes sein?
- Aynur vergleicht das blaue und grüne Rechteck und sagt: „Das blaue und das grüne Rechteck sind gleich groß.“ Hat sie Recht? Begründe.
- Orkan sagt: „Das orangefarbene und das hellblaue Dreieck sind gleich groß.“ Emily widerspricht: „Die beiden Dreiecke können nicht gleich groß sein, denn sie sehen unterschiedlich aus.“ Wer hat Recht? Begründe.
- Das blaue Rechteck und das hellblaue Dreieck sind gleich groß. Überlege und begründe, warum das so ist.
Die Lernenden können ihre Aussagen ...
- verbal begründen: „Das blaue und das grüne Rechteck müssen gleich groß sein, weil das gleich große Ausgangsrechteck zweimal halbiert wird.“
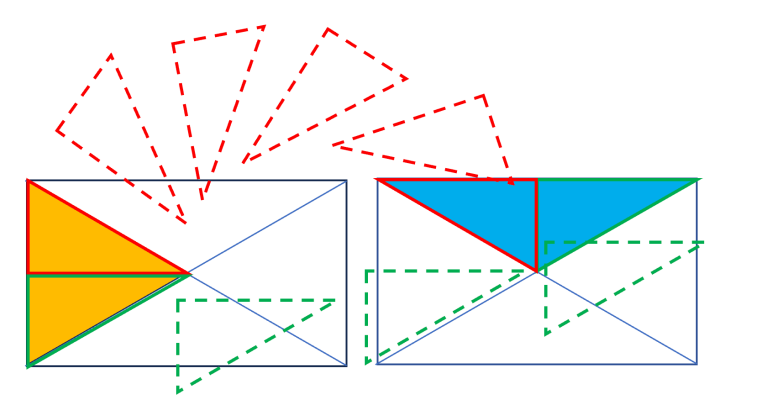
- materialgestützt begründen, indem sie Faltungen und Teile zerschneiden (s. o. und Abb. 3), Teile aufeinander- bzw. umlegen und diese Handlungen beschreiben: „Das orangefarbene Dreieck wird entlang seiner Höhe zerschnitten und dann zu dem hellblauen Dreieck umgelegt.“ (s. Abb. 4).
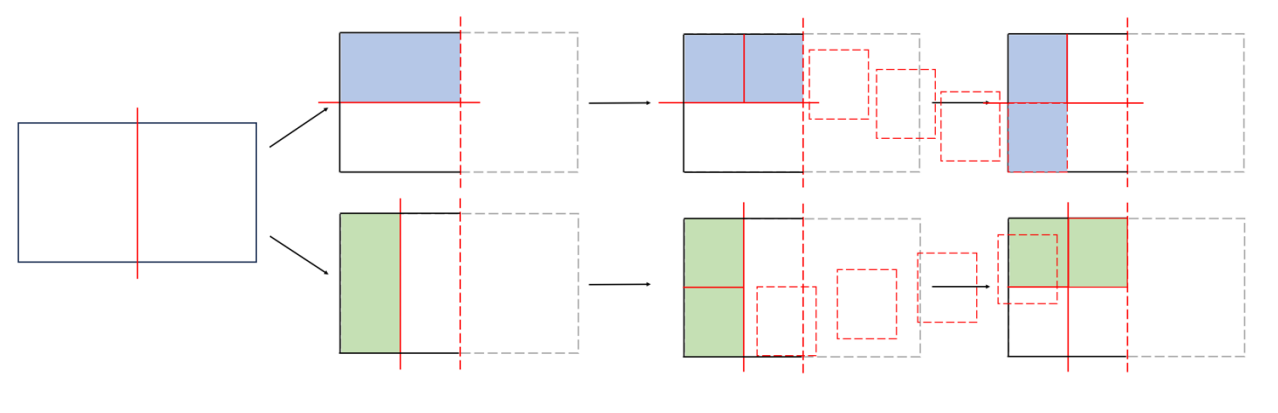
Abbildung 3: Beispiel für die Darstellung einer Begründung durch Falten, Zerschneiden und Umlegen
Hinweise zur sprachlichen Unterstützung
An dieser Stelle kann die Lehrkraft die Einführung erster Fachbegriffe durch gezielte Gesprächsimpulse unterstützen:
-
Beobachtungen anregen: „Was stellt der jeweils gefärbte Teil dar?“
Es handelt sich um einen Teil eines Ganzen, genau gesagt, um ein Viertel. - Fachbegriffe einführen: „In der Mathematik gibt es für diesen Teil einen bestimmten Begriff – wisst ihr, wie man diesen Teil nennt?“ Der Begriff ein Viertel wird eingeführt.
- Bedeutung klären: Die Lernenden äußern Vermutungen zur Wortbedeutung („eins von vier Teilen“). Die Lehrkraft ergänzt bei Bedarf: „Ein Viertel ist einer von vier gleich großen Teilen eines Ganzen.“
- Weitere Beispiele finden: „Welche anderen Begriffe kennt ihr, die auch einen Teil eines Ganzen bezeichnen?“ (ein Drittel, drei Viertel, ein Fünftel,…)
- Fachbegriff „ein Anteil“: Die Lehrkraft erläutert den Begriff „ein Anteil“: Ein Anteil beschreibt, in welchem Verhältnis ein Teil zum Ganzen steht.
Hinweis:
Anders als in den anderen Aufgabenstellungen kompakt, die auf den Seiten von Mathe inklusiv mit PIKAS zu finden sind, bauen die folgenden Basisaktivitäten aufeinander auf. So sollte das Falten weiterer Anteildarstellungen vor den anderen Basisaktivitäten durchgeführt werden und das Verknüpfen verschiedener Anteildarstellungen erst dann erfolgen, wenn die Lernenden bereits eine oder mehrere Basisaktivitäten bearbeitet haben.
Basisaktivität
Falten weiterer Anteildarstellungen
„Faltet Rechtecke in gleich große Teile. Findet unterschiedliche Möglichkeiten. Färbt jeweils einen Teil. Erstellt Plakate für unterschiedliche Anteile.“
Material: Papierrechtecke in verschiedenen Größen, Stifte, Plakate, Kleber
Mit dieser Aufgabe vertiefen die Lernenden die Grundvorstellung Bruch als Anteil. Sie erkennen, dass Anteile sich immer auf ein Ganzes beziehen, Anteile eines Ganzen immer gleich groß sind und gleiche Anteile unterschiedlich aussehen können.
Die Lernenden erhalten rechteckiges Papier in verschiedenen Größen und finden möglichst viele Lösungen, Darstellungen zu den ausgewählten Anteilen zu falten und zu färben. Für einzelne Lernende können ausgewählte Hinweise hilfreich sein (z.B. Teile müssen nach dem Falten nicht exakt aufeinanderliegen, Rechteck nach dem Falten aufklappen und Teilflächen weiter falten, Blatt vor dem Falten ausmessen). Werden Blätter mehrfach gefaltet, können die Faltungen ungenau und auch unmöglich werden. In diesem Fall können Faltungen durch das Abmessen und Zeichnen von Linien mit einem Lineal ersetzt werden. Dies setzt voraus, dass die Lernenden Faltvorgänge in ihrer Vorstellung durchführen und genau zeichnen können.
Die Lernenden erstellen mit den gefalteten Papieren im Rahmen einer Gruppenarbeit ein Plakat zu dem ausgewählten Anteil. Hierzu diskutieren sie, welche Anteildarstellungen gleich sind und deshalb nur einmal auf das Plakat geklebt werden können und ob es noch weitere Möglichkeiten der Faltung gibt.
In der Reflexion präsentieren die Gruppen ihre erstellten Plakate und erklären und begründen ihre Faltungen und Färbungen.
Plakat "Ein Achtel"

Mögliche Fragen für die Reflexion:
- Welche Gemeinsamkeiten und Unterschiede haben die Anteile / Rechtecke auf dem Plakat?
- Welche weiteren Möglichkeiten gibt es, Rechtecke zu falten?
- Welche Faltungen passen gut auf dieses Plakat? Welche Faltungen passen nicht so gut? Begründe.
- Zwei Rechtecke wurden gleich gefaltet und unterschiedlich gefärbt. Warum sind die Anteile gleich und nicht unterschiedlich?
Unterschiedlich aussehende Teile
- Bei manchen Faltungen sehen nicht alle Teile gleich aus. Warum ist trotzdem immer der gleiche Anteil dargestellt?
Umgang mit doppelten Faltungen

Abbildung 7: Beispiel für ein Plakat mit doppelten Faltungen
- Joshua sagt: „Diese drei Faltungen sind gleich und damit doppelt.“ Welche Faltungen könnte er meinen? Begründe.
- Würdet ihr zwei der Faltungen, die Joshua meint, aussortieren? Begründet.
- Überlegt euch für diese Gruppe Tipps, wie sie doppelte Faltungen vermeiden könnte.
- Bei der Faltung rechts unten wurde zuerst zu viel gefärbt und dann ein Teil weiß gefärbt. Welcher Anteil wurde weiß gefärbt? Welcher Anteil wäre gefärbt, wenn nichts weißgefärbt worden wäre?
Basisaktivität
(Digitales) Sortieren rechteckiger Anteildarstellungen
„Findet Rechtecke, die in gleich große Teile geteilt sind.“
Material: Tablet und Sortierdateien (PPT Dateien) oder Materialausdruck Rechteckige Anteildarstellungen (DOCX/ PDF Datei)
In dieser möglichen Basisaktivität unterscheiden die Lernenden zwischen Ganzen, die in gleich große Teile geteilt sind und Ganzen, die in unterschiedlich große Teile geteilt sind. Sie erfahren, dass es sich nur dann um die gesuchten Anteile handelt, wenn alle Teile gleich groß sind, und vertiefen so ihr Verständnis von Anteilen.
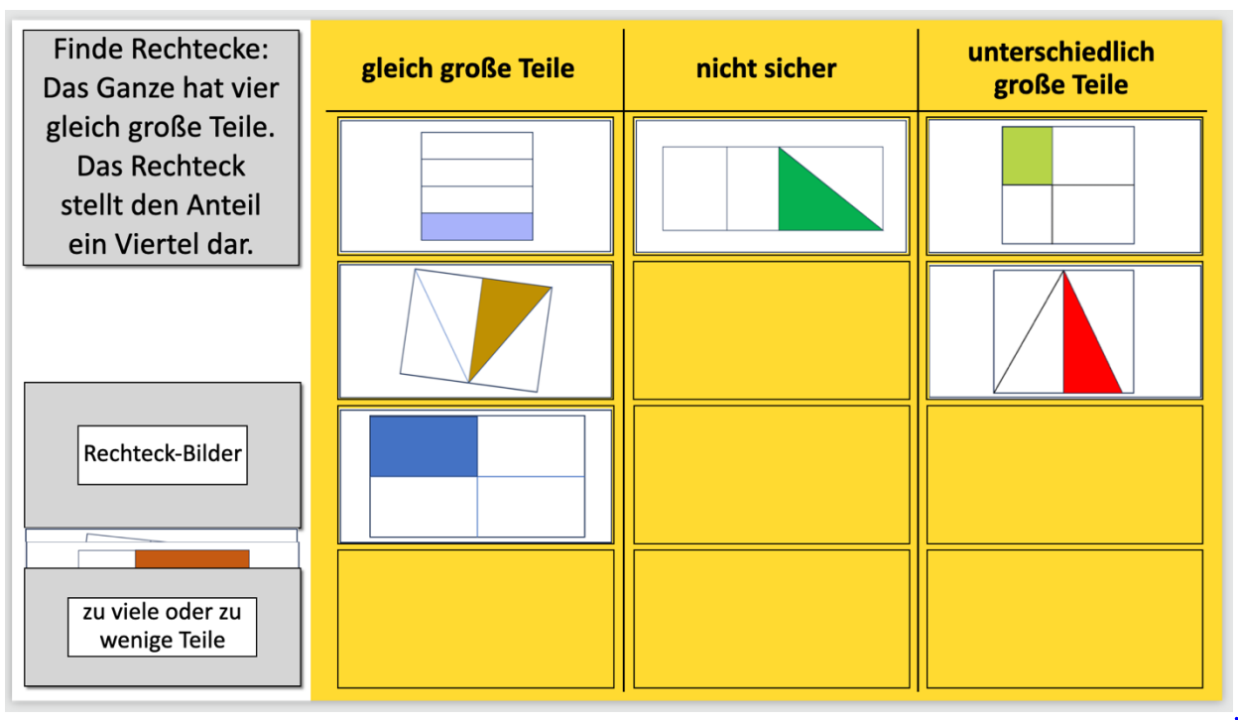
Die Lernenden sortieren entweder digital (zum Beispiel an einem Tablet) oder mit vorbereitetem Material unterschiedliche Rechteckabbildungen zu jeweils einem vorgegebenen Anteil in die Felder einer Sortiertafel: Hier gibt es die Kategorien „gleich große Teile“, „nicht sicher“, „unterschiedlich große Teile“ und „zu viele oder zu wenige Teile“ (für die digitale Umsetzung vgl. Abb. 8).
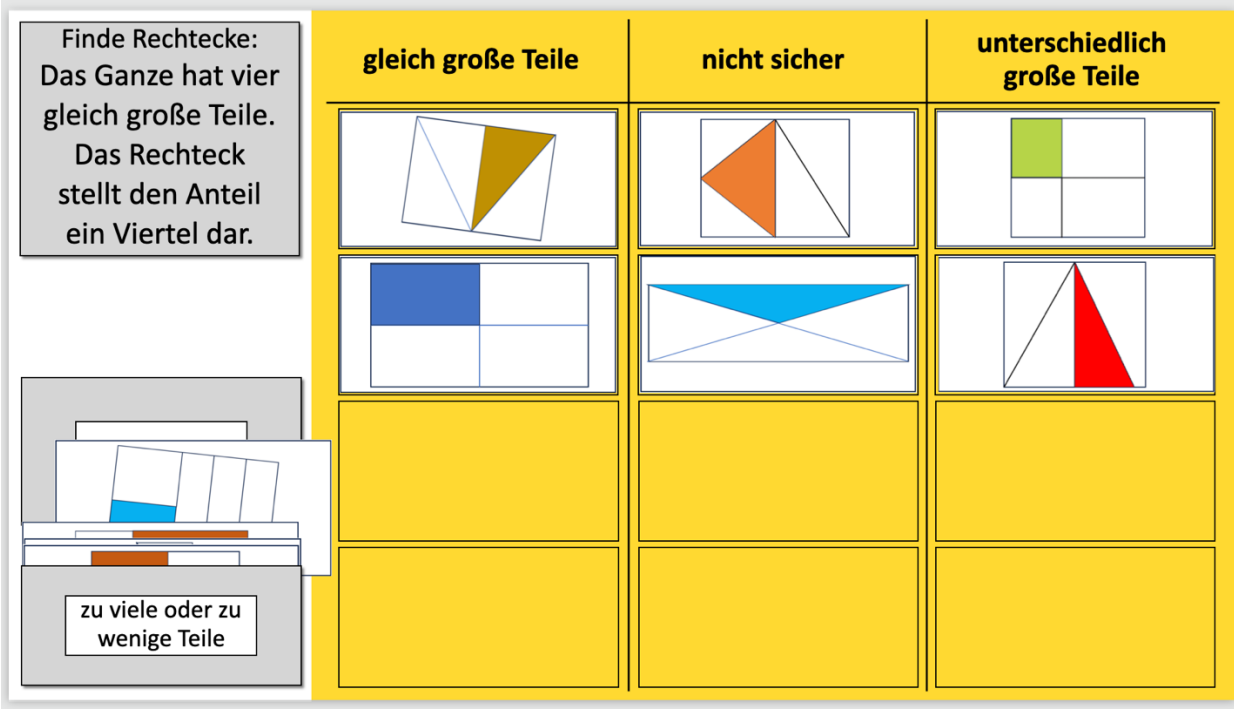
Einige der vorbereiteten Rechtecke weisen dabei Besonderheiten auf, die als Gesprächsanlässe genutzt werden können.
- Rechtecke, deren Teile teilweise unterschiedlich aussehen und alle groß sind. Diese Teile können im Kopf zerlegt und neu zusammengesetzt oder ausgemessen werden (s. o.).

- Rechtecke, die in unterschiedlich große und zu wenige bzw. zu viele Teile geteilt sind. Diese Rechtecke können zwei Feldern zugeordnet werden.
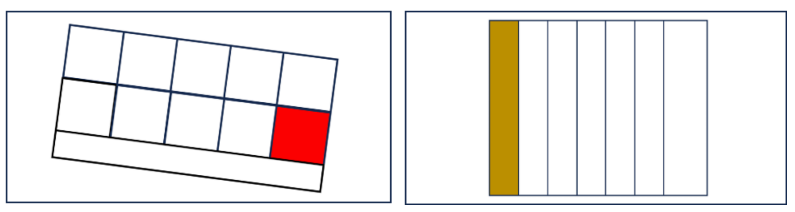
- Rechtecke, die in gleich große Teile geteilt sind, deren Anzahl aber größer oder kleiner ist als im Arbeitsauftrag genannt. Für diese Abbildungen schlagen wir das „zu wenige oder zu viele Teile“-Feld vor, da der mathematische Fokus auf der Darstellung des richtigen Anteils und nicht auf den gleich großen Teilen liegen sollte.
Fehlerhafte Abbildungen mit fünf bzw. drei gleich großen Teilen auf der Sortiertafel für den Anteil ein Viertel
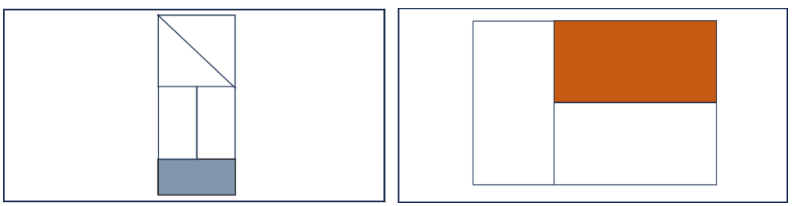
- Rechtecke, die in unterschiedlich große Teile geteilt wurden, bei denen das Ganze und der gefärbte Teil aber „trotzdem“ den gesuchten Anteil darstellt. Bei diesen Abbildungen entscheidet die Lehrkraft gemeinsam mit den Lernenden, ob die Karten in die Spalte „gleich große Teile“, „unterschiedlich große Teile“ oder bei der Nutzung des ausgedruckten Materials vielleicht sogar auf ein neues Feld gelegt werden. Diese Besonderheit kann als Gesprächsanlass genutzt und dann mit der Erweiterung „Sortieren ungewöhnlicher Anteildarstellungen“ vertiefend oder im Rahmen der Erweiterung behandelt werden. Im Mittelpunkt der Gespräche über diese Besonderheit sollte immer die Frage stehen, ob und warum die gefärbten Teile im Verhältnis zum Ganzen die gesuchten Anteile darstellen oder nicht.
Beispiele für Abbildungen mit unterschiedlich großen Teilen
Arbeit mit der Sortiertafel
Die Lernenden arbeiten mindestens zu zweit an einem Kartensatz mit der Sortiertafel bzw. an einem Tablet, wählen abwechselnd eine Karte aus, sortieren diese in die entsprechende Spalte ein und begründen ihre Wahl.
Im nächsten Schritt werden die Sortierungen in Kleingruppen (oder gemeinsam) überprüft und Karten aus der Spalte „nicht sicher“ zugeordnet. Dabei sollen die Lernenden ihre Sortierung auch weiterhin immer begründen.
Abschließend werden die Sortierungen dokumentiert (digital durch die Speicherung der Dateien mit den sortierten Abbildungen, beim Materialsatz durch ein Foto) und exemplarisch präsentiert.
Mögliche Begründungen:
- „Dieses Rechteck ist in sechs gleich große Teile geteilt, denn ich kann das Papier so falten, dass alle sechs Teile genau aufeinander liegen.“
- „In diesem Rechteck sind die Teile unterschiedlich groß. Wir haben das mit einem Lineal gemessen.“
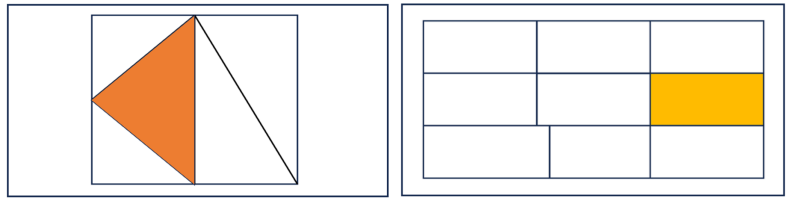
- „In diesem Rechteck (s. Abb. 13) sind alle Teile gleich groß. Ich kann das gefärbte Dreieck in zwei Teile zerlegen und beide Teile dann zu einem Rechteck zusammenlegen. Dieses Rechteck sieht genauso aus wie das andere Rechteck.“
Basisaktivität
Paare finden mit rechteckigen Anteildarstellungen
„Findet Rechtecke, die gleiche Anteile darstellen.“
Material: Materialausdruck Rechteckige Anteildarstellungen (DOCX/ PDF Datei)
Ziel dieser Basisaktivität ist es zu erkennen, welche Rechtecke den gleichen Anteil zeigen, obwohl sie verschieden groß, unterschiedlich aufgeteilt oder anders ausgerichtet sind. Außerdem sollen die Rechtecke erkannt werden, die nicht in gleich große Teile aufgeteilt sind.
Handlungsleitend sind die folgenden Fragen:
- „In wie viele Teile wurde das Rechteck geteilt?“
- „Sind alle Teile dieses Rechtecks gleich groß?“
- „Wie begründest du deine Zuordnung?“
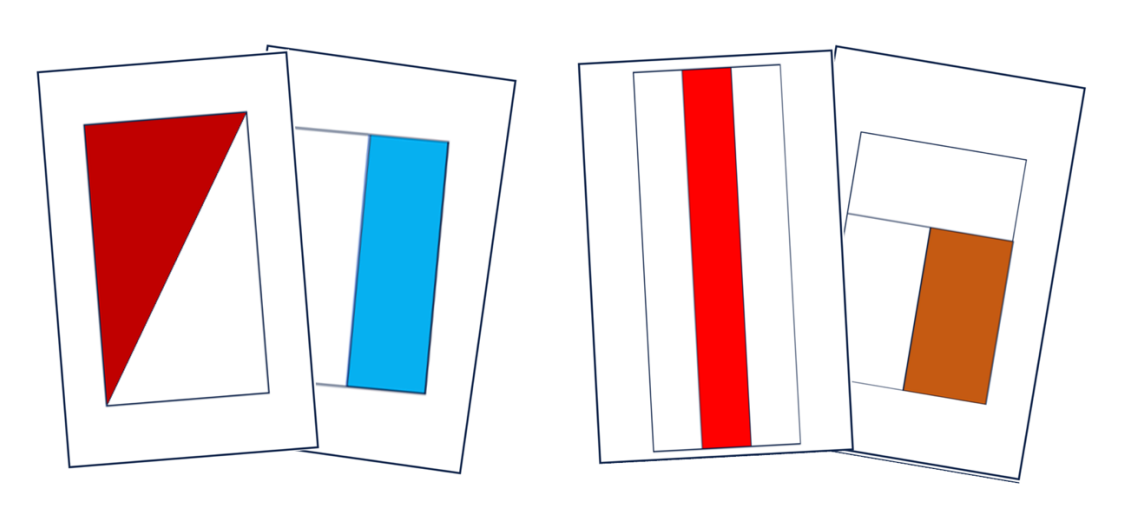
Die Lernenden arbeiten in Kleingruppen und erhalten mehrere Kartensets. Jeweils sechs Karten bilden ein Set. Vier von den sechs Karten eines Sets stellen einen Anteil korrekt dar, die zwei übrigen Karten sind Distraktoren: Sie stellen den Anteil nicht korrekt dar.
Durch eine bewusste Auswahl der Karten bzw. ihrer Anzahl ist eine Anpassung an das Kompetenzniveau der Lerngruppe möglich.
Die Kleingruppe legt die Karten offen auf den Tisch und ordnet immer zwei Karten begründet einander zu. Am Ende gibt es Kartenpaare mit falschen Anteildarstellungen und die Kartenpaare mit korrekten Anteildarstellungen können zu Quartetten zusammengelegt werden.
Spielideen
Mit den Karten können auch verschiedene Spiele gespielt werden, z. B. Memory, Quartett oder Paare finden. Auch hier kann durch eine bewusste Auswahl der Karten das Anforderungsniveau eines Spiels angepasst werden.
Beispiel: Paare finden
Die Karten werden gemischt und verteilt. Wer ein zusammengehöriges Paar Karten auf der Hand hat, darf dieses ablegen. Anschließend ziehen die Spielenden im Uhrzeigersinn reihum jeweils eine Karte bei ihren Mitspielenden und legen die Paare ab, die sie dadurch bilden können. Die Passung der abgelegten Paare muss begründet werden. Paare mit unterschiedlich großen Teilen werden ebenfalls abgelegt, zählen aber nicht als Anteilpaare.
Gewonnen hat, wer am meisten Anteilpaare ablegen konnte.
Basisaktivität
Verknüpfen verschiedener Anteildarstellungen
„Findet Abbildungen und Beschreibungen, die gleiche Anteile darstellen.“
Material: Verknüpfen verschiedener Anteildarstellungen (DOCX/ PDF Datei)
Ziel der Basisaktivität ist es, das an Rechtecken entwickelte Verständnis von Anteilen auf weitere Darstellungen wie Quadrat, Bruchstreifen und Kreis zu übertragen.
Die Lernenden arbeiten in Kleingruppen. Sie erhalten Beschreibungen, Kreis-, Rechteck-, Bruchstreifen- und/oder Quadratabbildungen von Anteilen. Ihre Aufgabe ist es nun, auf einer Sortiertafel die Karten mit gleichen Anteilsdarstellungen einander zu zuordnen.

Das Material enthält Karten zu neun verschiedenen Teilanzahlen. Bei Bedarf kann die Kartenauswahl um Distraktoren erweitert werden (siehe Datei). Die Karten umfassen Darstellungen in Form eines Rechtecks, eines Kreises, eines Bruchstreifens und eines Quadrats sowie Beschreibungen.
Die Startkarte auf der Sortiertafel kann sowohl eine der Bruchdarstellungen sein als auch eine Karte mit der Beschreibung (s. Abb. 15).
Auch hier gibt es die Möglichkeit, die Aufgabenstellung durch die bewusste Auswahl von Karten zu differenzieren:
Bewusste Auswahl hinsichtlich der …
-
Darstellungsformen (alle oder ausgewählte Formen)
-
Anzahl der Karten insgesamt
-
Anzahl der Karten für eine Reihe (Trio; Reduktion: Duo)
-
Anzahl der Distraktoren
Anregungen zur Arbeit mit der Sortiertafel:
- Sortieren aller Karten mit der gesamten Lerngruppe: „Wie viele verschiedene Anteil-Trios finden wir?“
- Sortieren ausgewählter Karten oder Kartenreihen in einer Kleingruppe: „Findet Anteil-Trios“
- Die Karten liegen offen auf dem Tisch oder werden reihum einzeln aufgedeckt oder von den Lernenden auf der Hand gehalten
-
Die Zuordnungen müssen immer begründet werden:
- Warum passen die Abbildungen zusammen?
- Erklärt, wie diese Abbildungen zueinander passen.
- Warum habt ihr diese Karte aussortiert?
- Wie habt ihr erkannt, dass dieses Ganze unterschiedlich große Teile enthält?
Reduktion
Falten ausgewählter Rechteckformen in 2 und 4 gleich große Teile
Material: Rechtecke unterschiedlicher Größe und Seitenverhältnissen, Stifte, Plakate, Kleber
Es gibt Lernende, denen es noch schwerfällt, eigene Ideen für Faltungen zu entwickeln oder die schnell aufgeben. Hier kann es eine Unterstützung sein, ihnen zunächst die Aufgabe zu geben, ein Papier in zwei gleich große Teile zu falten. Daran anschließend können die beiden Teile erneut gefaltet werden, so dass vier gleich große Teile entstehen. Die Lehrperson kann als weitere Hilfestellung Faltlinien einzeichnen oder den Anfang der Faltlinien andeuten.
- Finde verschiedene Möglichkeiten, das Blatt in zwei (vier) gleich große Teile zu falten.
- Welche Möglichkeiten gibt es, in einem Rechteck senkrecht, waagerecht oder diagonal zu falten und gleich große Teile zu erhalten?
Die gefalteten Rechtecke werden auf ein Plakat geklebt und in der Kleingruppe/ Gesamtgruppe reflektiert.
Reduktion
(Digitales) Sortieren rechteckiger Anteildarstellungen
„Findet Rechtecke, die in gleich große Teile geteilt sind.“
Material: Tablet und Sortierdateien (PPT Dateien) oder Materialausdruck Rechteckige Anteildarstellungen (DOCX/ PDF Datei)
Die Lernenden sortieren (ausgewählte) Karten aus dem Materialausdruck in die Sortiertafel. Dieser Kartensatz kann bei Bedarf um Distraktoren ergänzt werden (siehe Datei). Eine weitere Unterstützung kann es sein, die Lernenden zunächst zu den Anteilen ein Halbes und ein Viertel arbeiten zu lassen.
Reduktion
Paare finden mit ausgewählten rechteckigen Anteildarstellungen
„Findet Rechtecke, die gleiche Anteile darstellen.“
Material: Materialausdruck Rechteckige Anteildarstellungen (DOCX/ PDF Datei)
Die Karten für die Reduktion werden von der Lehrkraft aus dem Kartensatz der Basisaktivität ausgewählt. Die oben aufgeführte Basisaktivität kann wie folgt differenziert werden:
- Anzahl der Karten wird verringert (zwei oder vier Karten zeigen den gleichen Anteil)
- Der Distraktor pro Set wird herausgenommen vor dem ersten Spiel werden alle Karten offen auf den Tisch gelegt und gemeinsam einander zugeordnet (mit Begründung für die jeweilige Zuordnung)
- die Karten bleiben während des Spiels offenen liegen
Reduktion
Verknüpfen ausgewählter Anteildarstellungen
„Findet Abbildungen, die gleiche Anteile darstellen.“
Material: Verknüpfen verschiedener Anteildarstellungen (Aus diesem Materialsatz wählt die Lehrkraft – abhängig vom Vorwissen der Lernenden - Anteildarstellungen aus.)
Analog zur Basisaktivität „Verknüpfen verschiedener Anteildarstellungen“ erhalten die Lernenden unterschiedliche Darstellungen von Anteilen, aber eine von der Lehrperson bewusst gewählte und reduzierte Auswahl. Wie auch in der Basisaktivität kann die Startkarte wechseln und sowohl eine Anteilbeschreibung oder auch eine Abbildung sein.
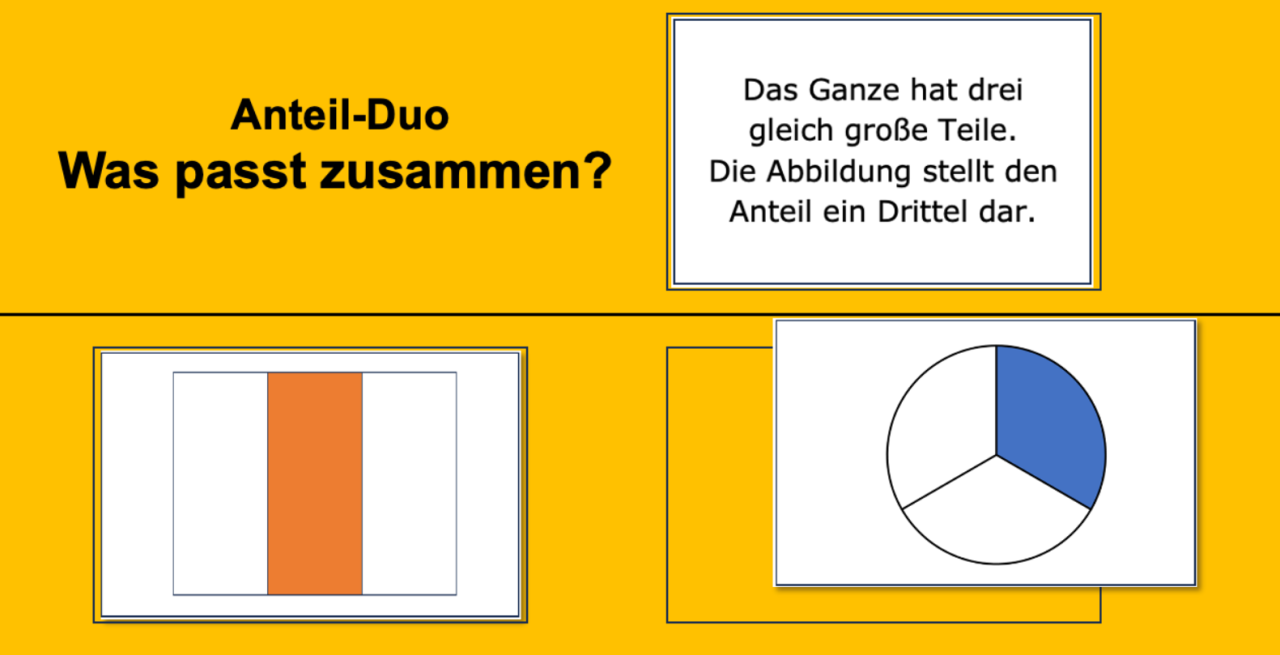
Analog zur Basisaktivität werden die Lernenden auch in dieser Aufgabe sowohl beim Zuordnen der Anteildarstellungen als auch beim Aussortieren von Ganzen mit unterschiedlich großen Teilen immer wieder aufgefordert, ihre Verknüpfungen sprachlich zu begleiten und sich untereinander auszutauschen.
Erweiterung
Falten weiterer Anteildarstellungen
Erkunden von Rechtecken, die in 3, 5, 6 und 7 gleich große Teile geteilt werden
Material: Papierrechtecke, Stifte, Plakate, Kleber
Die Erweiterung der Basisaktivität „Falten weiterer Anteildarstellungen“ besteht im Falten von rechteckigen Ganzen in 3, 5, 6 und 7 gleich große Teile. Die Lernenden arbeiten auch hier in einer Kleingruppe zusammen und finden zu einem Anteil möglichst viele Lösungen, die sie auf einem Plakat präsentieren. Es wird immer ein Teil des Ganzen farblich markiert.
Bei einer ungeraden Anzahl von Teilen führt das wiederholte Halbieren nicht zu einer Lösung. Die Lernenden sollen im Austausch in einer Kleingruppe Strategien diskutieren, erproben und überprüfen. Mögliche Strategien sind z. B.: Messen, ausprobierendes Falten, einzeichnen der Faltlinien, Berechnung des Verlaufs der Faltlinien oder die Nutzung von Hilfsmitteln.
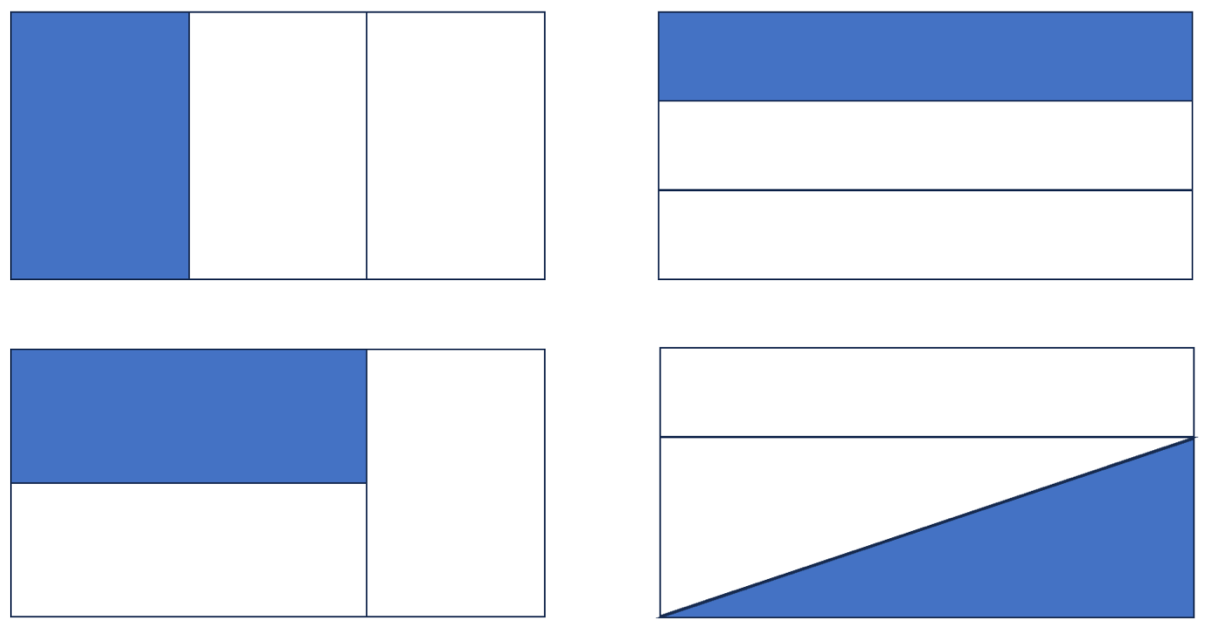
Durch das gemeinsame Nachdenken über weitere Darstellungsmöglichkeiten werden die Lernenden herausgefordert, eigene Ideen zu verbalisieren, mögliche Lösungswege zu beschreiben und ihre Vorgehensweisen und Anteildarstellungen zu begründen.
Mögliche Impulse:
- Finde verschiedene Lösungen, bei denen alle Teile genau gleich aussehen.
- Welche Lösungen findest du, bei denen Teile die gleiche Form haben und unterschiedlich aussehen?
- Wie könnte eine Lösung aussehen, bei der drei (vier, fünf, …, alle) gleich großen Teile unterschiedlich aussehen?
- Gibt es mehr Lösungen mit drei oder mit fünf gleich großen Teilen? Begründe deine Vermutung. Finde Beispiele für deine Vermutung.
- Warum sind die Teile deiner Faltung genau gleich groß?
- Wie bist du beim Einzeichnen der Faltlinien vorgegangen?
- Welche Tipps kannst du Lernenden geben, die keine Lösungen mehr finden?
- Wie kannst du berechnen, an welchen Stellen du die Faltlinien anzeichnen musst? Wie kannst du überprüfen, ob deine Berechnungen richtig sind?
Erweiterung
(Digitales) Sortieren ungewöhnlicher Anteildarstellungen
„Findet Rechtecke, die einen gesuchten Anteil darstellen.“
Material: Tablet und Sortierdateien (PPT Dateien) oder Materialausdruck Sortieren ungewöhnlicher Anteildarstellungen (DOCX/ PDF Datei)
Die Lernenden sortieren in dieser Erweiterung digital pro Präsentationsfolie oder mit vorbereitetem Material Anteildarstellungen in zwei Spalten mit Überschriften für verschiedene Anteile sowie in eine Spalte mit der Überschrift „nicht sicher“ und (digital) in ein Feld „ein anderer Anteil“. Die Benennung des Feldes kann zum Anlass genommen werden zu besprechen, dass jeder Teil eines Ganzen ein Anteil ist, auch wenn dieser auf den Abbildungen nicht genau zu bestimmen ist.
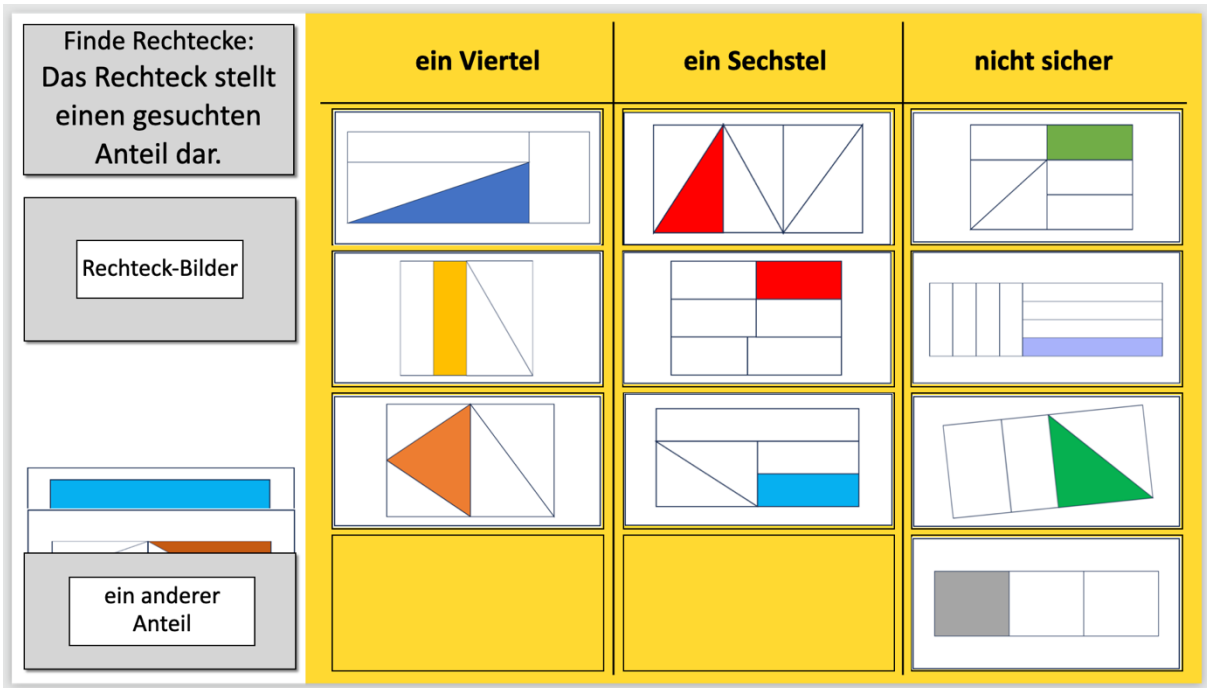
Die Herausforderung besteht darin, Abbildungen auch dann als gesuchte Anteildarstellungen zu erkennen, wenn das Ganze in verschieden große Teile oder in mehr oder weniger Teile geteilt wurde, als der gesuchte Anteil nahelegt. Die Lernenden müssen dazu Beziehungen zwischen dem gefärbten Teil und dem Ganzen herstellen, mit denen sie begründen können, warum das Rechteck einen gesuchten Anteil darstellt oder nicht.
Ebenso wie in der Basisaktivität ist es auch hier wichtig, dass die Lernenden Sortierentscheidungen den anderen Gruppenmitgliedern/ anderen Gruppen gegenüber begründen, Begründungen kritisch hinterfragen und gegebenenfalls widerlegen. Erste Ideen für Begründungen können gemeinsam beschrieben und durch Messen der entsprechenden Seiten „bewiesen“ oder verworfen werden.
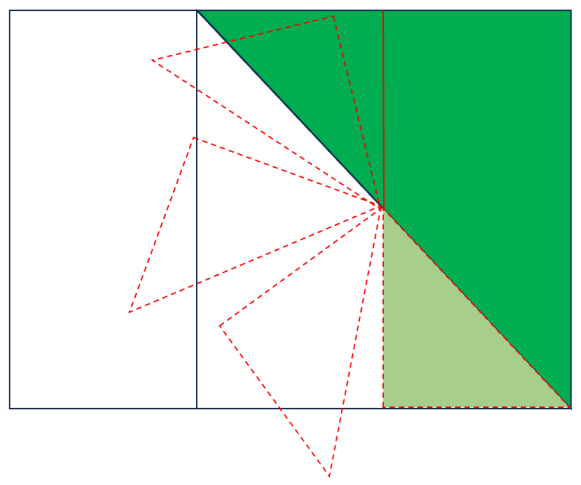
Mögliche Begründungen für die Sortierentscheidungen:
- „Das rote Dreieck ist ein Sechstel, denn die kurze Seite ist halb so lang wie die beiden rechts davon liegenden kurzen Seiten zusammen.“
- „Das braune Dreieck stellt ein Viertel des Ganzen dar. Wenn ich die beiden kleineren Dreiecke zusammenlege, sind sie genauso groß wie das braune Dreieck. Und die drei Dreiecke zusammen sind so groß, wie die Hälfte des ganzen Rechtecks.“
- „Das große hellblaue Rechteck stellt ein Drittel des Ganzen dar und damit einen anderen Anteil. Wenn ich drei von den hellblauen Rechtecken übereinanderlege, sind die zusammen so groß wie das ganze Rechteck. Das habe ich am Bildschirm gemessen und ausgerechnet.“
Erweiterung
Herstellen verschiedener Anteildarstellungen
„Wählt gemeinsam einen neuen Anteil aus. Stellt diesen Anteil mit einem Kreis, einem Rechteck, einem Streifen und einem Quadrat dar.“
Material: Karopapier, Stifte, Lineal, evtl. Zirkel
Die Lernenden erstellen in dieser Erweiterung für Anteile ihrer Wahl eigene Kreis-, Rechteck-, Streifen- und Quadratdarstellungen.
Sie einigen sich in ihrer Gruppe auf einen Anteil und erstellen arbeitsteilig die entsprechenden Darstellungen. Dabei erklären und begründen sie gegenüber den anderen Gruppenmitgliedern ihre Überlegungen und Darstellungen, erhalten Rückmeldungen und überarbeiten bei Bedarf ihre Darstellungen.
Karopapier kann bei der Erstellung der Rechteck-, Streifen- und Quadratdarstellungen helfen. In der Regel sollten die Lernenden vor dem Zeichnen überlegen, welche Maße ihre Darstellung bekommen soll, damit die Kästchen eine Unterstützung darstellen und keine Hürde.

Die Darstellung in einem Kreismodell kann mit den Mitteln, die ihnen zur Verfügung stehen, nur ungefähr die exakten Anteile zeigen. Für das Ziel der Einheit ist das genaue Zeichnen von untergeordneter Bedeutung, sollte aber mit den Lernenden besprochen werden.
Möglichkeiten individueller Unterstützung
Vorgeben von Faltlinien
Das Falten kann für die Lernenden durch Markierungen erleichtert werden. Dabei können entweder kleine Markierungen an den Seiten des Papiers vorgegeben werden oder aber durchgängige Faltlinien.

Weiterführend können Markierungen bzw. Linien für diagonale Faltungen eingezeichnet werden. Die Lernenden sollen die Markierungen und Faltlinien zunehmend selbständig einzeichnen.
Möglichkeiten individueller Unterstützung
Verwenden einer Faltanleitung
Eine weitere Möglichkeit zur individuellen Unterstützung ist eine Faltanleitung. Hier wird das genaue Falten Schritt für Schritt erklärt. Es besteht auch die Möglichkeit, dass die Lernenden selbst eine Faltanleitung erarbeiten.
Das könnte zum Beispiel folgendermaßen aussehen:
-
Überlege dir, welche beiden Seiten des Papiers aufeinanderliegen sollen. Lege eine Seite des Papiers an eine gerade, aufrechte Fläche (z. B. einer Wand, eines Schranks oder eines Fensterrahmens), die nicht verrutschen kann.

Abbildung 22: Faltanleitung Schritt 1 -
Lege nun die gegenüberliegende Seite des Papiers auf die Seite an der Wand, sodass beide Seiten die Wand berühren.

Abbildung 23: Faltanleitung Schritt 2 -
Halte beide Seiten mit den Fingern einer Hand so fest, dass sie an der Fläche liegen und sich nicht verschieben lassen. Drücke dann mit einem Finger der anderen Hand auf die Faltlinie und falte das Papier.

Abbildung 24: Faltanleitung Schritt 3 -
Du kannst so auch die Hälfte von einer Hälfte falten. Lege dazu die mittlere Faltlinie an die Wand und führe die gleichen Schritte durch.

Abbildung 25: Faltanleitung Schritt 4
Möglichkeiten individueller Unterstützung
Für das Beschreiben und Erklären Sprachmuster verwenden und einen Sprachspeicher anlegen
Das Beschreiben der Entdeckungen und Vorgehensweisen kann durch das Anlegen eines Sprachspeichers und die Vorgabe von Sprachmustern und Satzbausteinen unterstützt werden (vgl. hierzu auch Förderschwerpunkt Sprache: Unterricht).
Zentrale Mathewörter
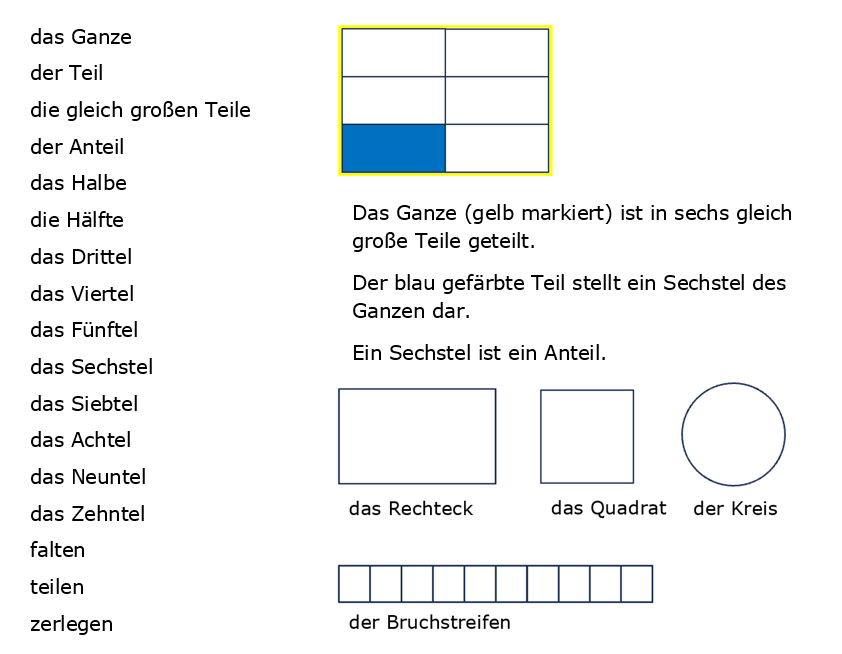
Mögliche Sprachmuster/Satzbausteine
- Das Ganze hat (z. B. drei, vier) Teile. Ein Teil stellt deshalb ein (z. B. Drittel, Viertel) dar.
- Dieser Teil ist größer/kleiner als die anderen Teile. Deshalb ist das Ganze nicht in (z. B. drei, vier) gleich große Teile geteilt.
- Ich habe das Rechteck an dieser Stelle gefaltet, weil …
- In dieser Darstellung ist auch ein (z. B. Drittel, Viertel) gefärbt, weil …


