Frühe mathematische Kompetenzen im Bereich Raum und Form
Vor dem Schuleintritt sollten Kinder idealerweise erstes grundlegendes Wissen und erste Fähigkeiten im Bereich Raum und Form erworben haben, auf welches dann ab der Schuleingangsphase und bis in die Sekundarstufe I hin im Sinne des Spiralprinzips kontinuierlich aufgebaut werden kann (s. auch Leitideen: Kontinuität herstellen). Zu den frühen mathematischen Fähigkeiten (im Lehrplan NRW benannt als „Vorläuferfähigkeiten“) im Bereich Raum und Form werden im Lehrplan Mathematik für die Primarstufe in Nordrhein-Westfalen u. a. das Erkennen geometrischer Formen (Kreis, Dreieck, Viereck) und das Wahrnehmen, Sortieren, Klassifizieren von Unterschieden und Ähnlichkeiten gezählt (MSB NRW, 2021, S. 81). Das Sortieren von Gegenständen nach Merkmalen ist eine Tätigkeit, die Kinder aus Kindertagesstätten häufig schon kennen und wird in den Bildungsgrundsätzen des Landes Nordrhein-Westfalen als eine Bildungsmöglichkeit für das Mathematiklernen von Kindern im Übergang zur Schuleingangsphase formuliert (MSB NRW, 2018, S. 119).
In diesem Text zum theoretischen Hintergrund wird an dieser Stelle zunächst ein Überblick über die Potentiale der Tätigkeit des Sortierens geometrischer Formen gegeben, da die Förderung der Sortierkompetenzen und die damit einhergehende geometrische Begriffsbildung im Mittelpunkt der im Bereich Unterricht zur Verfügung gestellten Materialien stehen. Es wird vorgestellt, wie geometrische Formen kontinuierlich im Lernprozess der Kinder von der Kita bis zur Sekundarstufe I thematisiert werden und welche Begriffsgrundlagen – auch als Hintergrundwissen von Lehrkräften – zu geometrischen Formen wichtig sind.
Potentiale beim Sortieren geometrischer Formen
Das Erkennen geometrischer Formen kann durch das Sortieren von ebenen Figuren gefördert werden, da dafür von Kindern Gemeinsamkeiten und Unterschiede der Formen erfasst und herausgestellt werden müssen. Was genau unter Sortieren zu verstehen ist und welche Potentiale diese Tätigkeiten für den Mathematikunterricht besitzen, soll im Folgenden kurz dargestellt werden.
Das im Lehrplan beschriebene Sortieren und Klassifizieren (s. oben, MSB NRW, 2021, S. 81) wird von Franke und Reinhold als „Kategoriesuchendes Sortieren und Ordnen“ und „Kategoriegeleitetes Sortieren und Ordnen“ charakterisiert. Beim „Kategoriesuchenden Sortieren und Ordnen“ erhalten Kinder Objekte, die frei sortiert bzw. geordnet werden sollen. Beim „Kategoriegeleiteten Sortieren und Ordnen“ erfahren die Kinder vor dem Sortieren, wie sie sortieren bzw. ordnen sollen. Vorgaben können dabei sein: ein Prototyp des Objekts, eine Abbildung oder ein Begriffswort des Gegenstandes oder auch das Nennen klassenbildender Merkmale (Franke & Reinhold, 2016, S. 162f.). Es ist also jeweils das Ziel, dass Kinder Kategorien bilden. Entweder entstehen diese Kategorien im Prozess oder die Kategorien werden vorab bewusst vorgegeben. Dafür bedarf es gezielter Sortieraktivitäten.
Ein beispielhafter Arbeitsauftrag für das „Kategoriesuchende Sortieren und Ordnen“ ist: „Sortiere Formen. Erkläre und benenne deine Sortierung.“ Ein beispielhaftes Vorgehen dafür ist in dem Video „Kategoriebildendes Sortieren zu Eigenschaften von Formen“ zu sehen.
Video: Kategoriebildendes Sortieren zu Eigenschaften von Formen
Im Video ist zu sehen, dass beim Sortieren der Formen zunächst Ähnlichkeiten gesucht und die sortierten Formen anschließend nach ihrer Eigenschaft benannt und in Gruppen sortiert werden (die Größe der Formen: klein, mittel, groß, riesig). Ein beispielhafter Arbeitsauftrag für das “Kategoriegeleitete Sortieren und Ordnen“ ist „Sortiere alle Formen in die passenden Felder: vier Ecken, drei Ecken, keine Ecken“. Ein beispielhaftes Vorgehen dafür ist in dem Video „Kategoriegeleitetes Sortieren zu Eigenschaften von Formen“ zu sehen.
Video: Kategoriegeleitetes Sortieren zu Eigenschaften von Formen
Im Video ist zu sehen, dass die Eigenschaften der Kategorien, nach denen sortiert werden soll, schon im Vorhinein bekannt sind (die Eckenanzahl der Formen) und die Formen entsprechend der Eigenschaften identifiziert und sortiert werden.
Viele Kinder sortieren schon früh nebenbei und automatisch im Alltag. So sortieren sie bspw. beim Aufräumen nach Kategorien (z. B. alle Holzbausteine kommen in die große Kiste, alle Kunststoffbausteine in die bunte Kiste) oder sie sortieren Gegenstände frei (z. B. Muscheln, Aufkleber oder Spielzeugfiguren). Voraussetzung für das Sortieren der Gegenstände ist die analytische Auseinandersetzung mit Gemeinsamkeiten und Unterschieden von Objekten (Reuter, 2022). An diese spielerischen Tätigkeiten der Kinder des Sortierens im Alltag kann und soll im Mathematikunterricht angeknüpft werden, da dadurch grundlegende inhaltsbezogene und prozessbezogene Kompetenzen (insbesondere das Problemlösen, Kommunizieren und Argumentieren) gefördert werden können – diese werden im Folgenden für die Grundschule vorgestellt.
Kompetenzerwartungen beim Sortieren geometrischer Formen
Inhaltsbezogene Kompetenzen
Das Sortieren fördert bei Kindern die Fähigkeit, eine Gesamtmenge von Objekten in logisch sinnvolle Teilmengen zu unterteilen. Dabei erfordert es „die Analyse der Eigenschaften gegebener Formen“ (Ruwisch, 2011, S. 40). Die Teilmengen werden auf Grundlage spezifischer Merkmale gebildet. Einfache Unterscheidungen können z. B. durch die Teilmengen „groß und klein“ erfolgen. Bei einer umfassenderen Sortierung werden mehr als zwei Kriterien berücksichtigt, wie etwa die Anzahl der Ecken und die Größe von Formen oder Farbe und Größe der Formen (Jegodtka, 2017). Dabei gibt es abhängig von den jeweiligen Formen und Kategorien Sortierungen, die eindeutig sind (z. B. die Anzahl der Ecken) und solche, die nicht eindeutig sind (z. B. die Größe der Formen).
Zur Förderung früher mathematischer Kompetenzen im Bereich Geometrie können durch das Sortieren geometrischer Formen geometrische Begriffsbildungsprozesse angeregt werden. Die Lernenden sollen also beim Sortieren der Formen dazu angeregt werden zu lernen, wie bspw. der Name einer Form lautet, wie diese aussieht und wie diese beschrieben werden kann. „Ziel ist ein gelungenes Zusammenspiel von Definition, Darstellung und Begriffserklärung“ (Reuter, 2022).
Die Begriffsbildung durch das Sortieren von Formen entspricht dabei einem Begriffserwerb durch Abstrahieren (Franke & Reinhold, 2016, S. 132): Es werden Kategorien nach bestimmten Merkmalen gebildet, die von den Kindern beim Sortieren selbst entdeckt oder von der Lehrkraft vorgegeben werden. Daran anknüpfend kann eine Begriffsbildung durch das Bilden von Kategorien nach einer verbalen Beschreibung der Kinder durch die Nennung des Fachbegriffs erfolgen. Durch das Erfassen visueller Merkmale und das Beschreiben derselben begreifen die Kinder die Form. Besonders bei einem Zusammenspiel von Beispielen, verbaler Erläuterung und Gegenbeispielen kann die Begriffsbildung gelingen (ebd., S. 132; vgl. Zech, 2002, S. 260ff.).
Schauen wir uns als Beispiel das Quadrat an und wie Kinder dieses von anderen Formen abgrenzen könnten. Das Quadrat hat vier Ecken und vier genau gleich lange Seiten im rechten Winkel. Andere Formen können aufgrund ihrer unterschiedlichen Eigenschaften wie bspw. der Seitenlänge oder der Winkelgröße vom Quadrat abgegrenzt werden (Abb. 2). In der Abbildung 2 stellt sich die Frage, ob die oben abgebildeten Formen Quadrate sind. Die Begründungen für das Quadrat werden über die Abgrenzung zu den Eigenschaften der anderen Formen ermittelt. So wird beispielsweise festgestellt, dass eine Form kein Quadrat sein kann, wenn sie unterschiedlich lange oder schiefe Seiten hat.
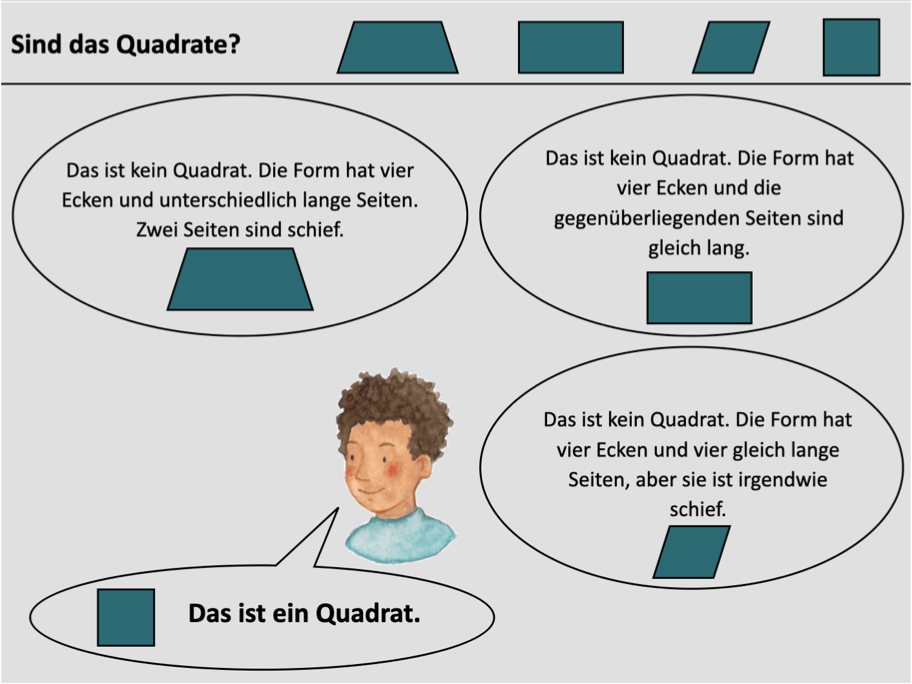
Abb. 2: Begründungen für das Quadrat über die Eigenschaften anderer Formen finden
Auch Unterhauser (2019) hebt beim Sortieren von Formen insbesondere die Bedeutung des Begründens von Sortierungen für die Begriffsbildung hervor. Dabei fällt es Kindergartenkindern leichter zu begründen, warum eine Form z. B. kein Quadrat ist, als Eigenschaften des Quadrats zu beschreiben. Definieren Kinder konkrete Formen, dann beziehen sie sich vor allem auf die Anzahl der Ecken und Seiten, aber auch Winkeleigenschaften und Seitenverhältnisse bzw. -längen werden zur Beschreibung von Formen genutzt (Unterhauser, 2019, S. 246).
Des Weiteren schult das Sortieren im Bereich der visuellen Wahrnehmung das genaue Beobachten und die Wahrnehmungsfähigkeit der Kinder. Insbesondere wird die Wahrnehmung der Formkonstanz gefördert, also die Fähigkeit, eine Form unabhängig von ihrer Größe oder Ausrichtung zu erkennen (Franke & Reinhold, 2016, S. 58). Beispielsweise können Kongruenzen oder Ähnlichkeiten identifiziert werden, wenn eine in der Hand gehaltene Form aus einer Menge verschiedener Formen anhand ihrer Eigenschaften untersucht wird (Franke & Reinhold, 2016, S. 59). Besonders beim Quadrat spielt die Ausrichtung der Form eine entscheidende Rolle. „Kann ein Quadrat in typischer Orientierung von bis zu ca. 90 % der Kinder korrekt identifiziert werden, so fällt die Identifikationsrate auf 60 % bis 70 %, wenn der Repräsentant um 45° auf die Ecke gedreht präsentiert wird.“ (Unterhauser, 2019, S. 215). Wenn den Kindern die Raute als Repräsentant ebenfalls bekannt ist, dann fällt es ihnen leichter, auch um 45° gedrehte Quadrate als Quadrate zu identifizieren (Maier, 2019, S. 243f.).
Prozessbezogene Kompetenzen
Auf Ebene der prozessbezogenen Kompetenzen können durch das Sortieren das Problemlösen, Kommunizieren, Darstellen und Argumentieren angesprochen werden.
Das Problemlösen (MSB NRW, 2021, S. 82) wird durch das Sortieren von Formen insofern angeregt, als dass die Kinder zunächst probierend und dann zunehmend systematisch vorgehen, dabei unterschiedliche Vorgehensweisen erkunden und Zusammenhänge zwischen den Formen erkennen. Beim Sortieren der Formen in Kategorien können die Lernenden Ideen für mögliche Vorgehensweisen entwickeln und dabei sukzessiv strukturiert und strategiegeleitet vorgehen. Die Aufgaben zum Sortieren und Erkunden von Formen können sowohl eigenständig, als auch im Austausch mit anderen bearbeitet werden.
Im Austausch mit anderen werden die Kinder dazu angeregt, u. a. die Sortierungen nachvollziehbar zu beschreiben, erläutern, begründen und für andere zu präsentieren (Kommunizieren) (MSB NRW, 2021, S. 83). Zum Kommunizieren über die Formen benötigen die Kinder Wissen über geometrische Begriffe: die geometrischen Objekte, Eigenschaften und Relationen (Franke & Reinhold, 2016, S. 21f.), die in der Klasse gemeinsam erarbeitet werden sollen. Insbesondere durch das Vorstellen der Lösungswege für andere, das Beschreiben der Sortierungen und Benennen dieser wird die prozessbezogene Kompetenz des Kommunizierens durch die Aufgabenstellung gefördert.
Im Bereich des Argumentierens können unterschiedliche Kompetenzen gefördert werden. Die Lernenden vergleichen die geometrischen Formen im Hinblick auf Zusammenhänge, Gemeinsamkeiten und Unterschiede und erklären „allgemeine Überlegungen in Bezug auf Beziehungen und Gesetzmäßigkeiten anhand von Beispielen“ (MSB NRW, 2021, S. 84). Vorgehensweisen beim Sortieren und Kategorienbilden sollten nachvollziehbar begründet werden (MSB NRW, 2021, S. 84).
Auch „verbale[n] Fähigkeiten werden gefordert, denn entsprechend der Auswahlkriterien (Eigenschaften finden oder Eigenschaften nutzen) sind Gruppierungen zu begründen. Hierzu können auch Steckbriefe für die verschiedenen Figuren angefertigt werden“ (Primakom, o. J.). Um das Begründen weiter zu fördern, können Fragestellungen unterstützen, wie „Welche Formen gehören zusammen und warum?“. Dabei ist es wichtig, dass zuvor nicht festgelegt ist, welche Lösung als falsch oder richtig anerkannt wird. Es ist zentral, dass rahmend eine angstfreie Fehlerkultur herrscht, in der es „richtige Lösungen“ und „nachvollziehbare und weniger nachvollziehbare Begründungen“ gibt (Reuter, 2022). Zur sprachlichen Unterstützung können die Lernenden auf einen Sprachspeicher zurückgreifen, der auf Grundlage der im Unterricht stattfindenden Gespräche über die Eigenschaften der Formen gemeinsam entwickelt werden kann.
Die prozessbezogene Kompetenz des Darstellens wird insbesondere dadurch gefördert, dass Kinder analoge Darstellungen (Formen) für das Bearbeiten der Aufgabenstellungen einsetzen und diese zur Präsentation der mathematischen Eigenschaften der Formen nutzen (MSB NRW, 2021, S. 85)
Kontinuität der Kompetenzerwartungen beim Sortieren geometrischer Formen
Neben den oben genannten Möglichkeiten des Sortierens nach Kriterien wie Eckenanzahl, Farbe, Art und Größe der Form gibt es natürlich auch noch eine Vielzahl weiterer Möglichkeiten, Formen zu sortieren, z. B. über die Anzahl der Seiten, Symmetrieeigenschaften, Regelmäßigkeiten, Kongruenzeigenschaften, Parallelität, Lagebeziehungen, Maße, Flächeninhalte oder Winkel. Aber wann sollen Kinder lernen, die unterschiedlichen Sortierkategorien in den unterschiedlichen Bildungseinrichtungen auch fachlich zu unterscheiden?
Welche Kompetenzen im Bereich Raum und Form in der Kindheit und Jugend erworben werden sollen, ist in den Bildungsgrundsätzen der Kindertageseinrichtungen und den Lehrplänen Mathematik Grundschule und Sekundarstufe I formuliert. „Die Kernideen des Geometrieunterrichts und die dazugehörigen Inhalte sind im Unterricht nach dem Spiralprinzip immer wieder aufzugreifen und zunehmend umfassender zu behandeln“ (Franke & Reinhold, 2016, S. 32, Hervorh. i.O.).
Die Bildungsgrundsätze für die Kindertagesbetreuung NRW formulieren im Bereich Raum und Form u. a., dass Kinder geometrische Grundformen und ihre Eigenschaften unterscheiden und in ihrer Umwelt wiedererkennen und „Gegenstände nach Merkmalen sortieren“ (MSB NRW, 2018, S. 116). (Hinweis: Die Bildungsgrundsätze stellen fachliche Handlungsgrundlagen und ein gemeinsames Bildungsverständnis für Kindertagesstätten in NRW dar und formulieren keine konkreten Kompetenzerwartungen.).
Darauf wird dann in der Grundschule aufgebaut. Wie auch schon zuvor beschrieben, werden in den Kernlehrplänen der Grundschule als frühe mathematische Fähigkeiten im Bereich Raum und Form u. a. das Erkennen geometrischer Formen (Kreis, Dreieck, Viereck) und das Wahrnehmen, Sortieren und Klassifizieren von Unterschieden und Ähnlichkeiten zur Anbahnung des Erkennens von Mustern genannt. Am Ende der Schuleingangsphase zählen zu den Kompetenzerwartungen weiterfühend die Identifikation der Grundformen (Rechteck, Quadrat, Dreieck, Kreis) und deren fachsprachliche Beschreibung (Seite, Ecke, Fläche). Bis zum Ende der vierten Klasse sollen Lernende weitere ebene Figuren wie u. a. das Sechseck, das Achteck und das Parallelogramm identifizieren und fachsprachlich (u. a. mit den Begriffen senkrecht, waagerecht, parallel, rechter Winkel) beschreiben können (MSB NRW, 2021, S. 90). In den Kernlehrplänen der Gesamtschule – Sekundarschule werden die bereits bekannten ebenen Figuren aufgegriffen (Rechteck, Quadrat, Parallelogramm, Dreieck, Kreis), die u. a. benannt, charakterisiert und in der Umwelt identifiziert werden sollen. Neu hingegen sind einige der verwendeten Grundbegriffe z. B. Punkt, Gerade, Strecke, Winkel, Abstand, Radius, parallel, senkrecht, achsensymmetrisch, punktsymmetrisch mit denen die Formen beschrieben werden (MSB NRW, 2019, S. 26).
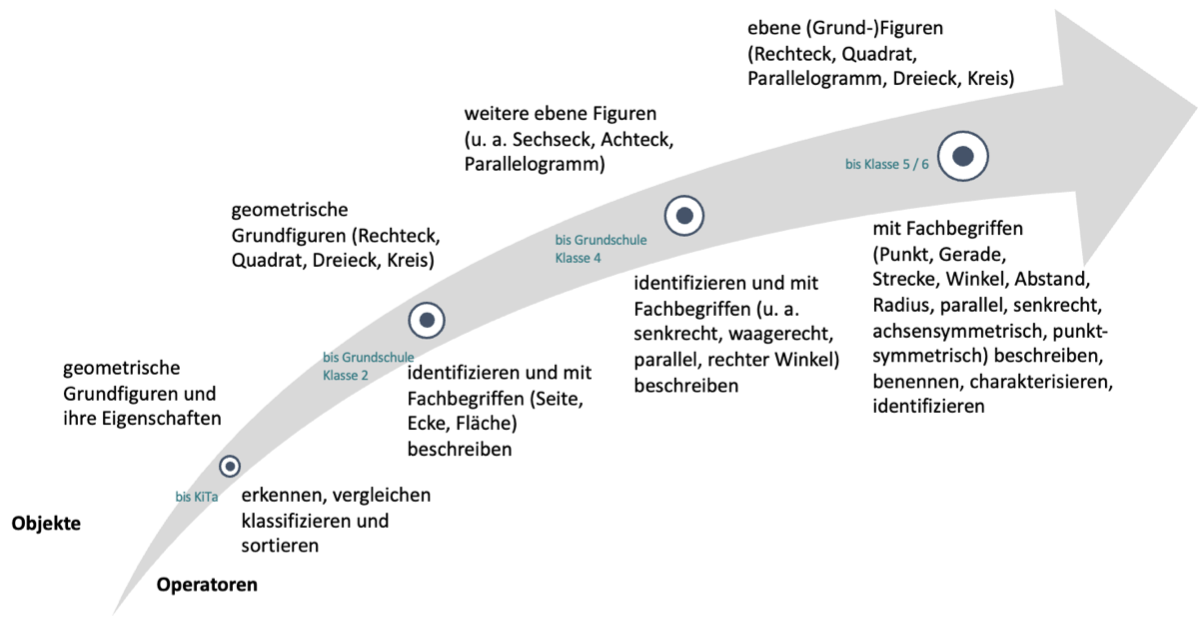
Abb. 3: Objekte und Operatoren zum Sortieren geometrischer Formen von KiTa bis Klasse 5/6 laut den Kernlehrplänen
Die Abbildung 3 zeigt im Überblick, wie sich die Objekte und Operatoren zum Sortieren geometrischer Formen im Bereich Raum und Form von der Zeit in der Kindertagesstätte über die Grundschule bis in die Sekundarstufe kontinuierlich weiterentwickeln und ausbilden.
Begriffsgrundlagen zu geometrischen Formen
Die folgenden Ausführungen geben einen Überblick über geometrische Begriffe, die für die Arbeit mit der nachfolgenden Aufgabenstellung Kompakt: Formen sortieren relevant sind. Es werden die Eigenschaften von Kreisen, Dreiecken, Vierecken und weiteren Vielecken vorgestellt, auf deren Grundlage schließlich sortiert werden kann. Ergänzend finden Sie auch auf Primakom ausführliche Hintergrundinformationen zu den Eigenschaften der ebenen Figuren Dreiecke, Vierecke, Vielecke und Kreise zur Entwicklung der Vorstellungen von Kindern zu ebenen Figuren und zu Aktivitäten, mit denen Sie an die Vorkenntnisse zu ebenen Figuren von Grundschulkindern anknüpfen können.
Eigenschaften von Formen
Um die Eigenschaften von geometrischen Formen zu erkunden, können in erster Annäherung die Anzahl der Ecken, Anzahl und Länge der Seiten und die Größe der Flächen betrachtet werden.
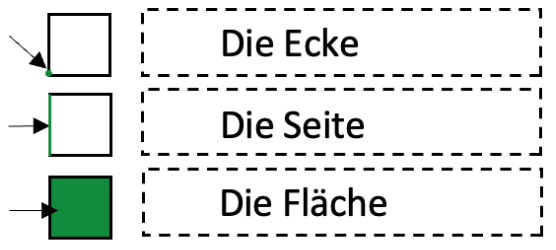
Abb. 4: Fachbegriffe: Ecke, Seite, Fläche
-
Die Ecke ist der Punkt, an dem zwei Seiten einer Fläche zusammentreffen.
-
Die Fläche wird von allen vier Seiten umschlossen.
-
Die Seite ist die Grenze einer Fläche und eine Linie, die zwei Ecken miteinander verbindet.
Darüber hinaus können weiterer Eigenschaften gelten wie z.B.:
-
Seiten können im 90 Grad Winkel zueinanderstehen oder bei anderen Winkelgrößen ganz unterschiedlich zueinanderstehen.
-
Seiten verlaufen parallel, wenn sie immer den gleichen Abstand voneinander haben.
Eigenschaften von Formen untersuchen
Beim Untersuchen der Eigenschaften der Formen können die Kinder z. B. Seitenlängen oder Flächen relational vergleichen und beschreiben und dabei auf die Beziehungen kurz/kürzer bzw. lang/länger bzw. gleich/unterschiedlich eingehen.
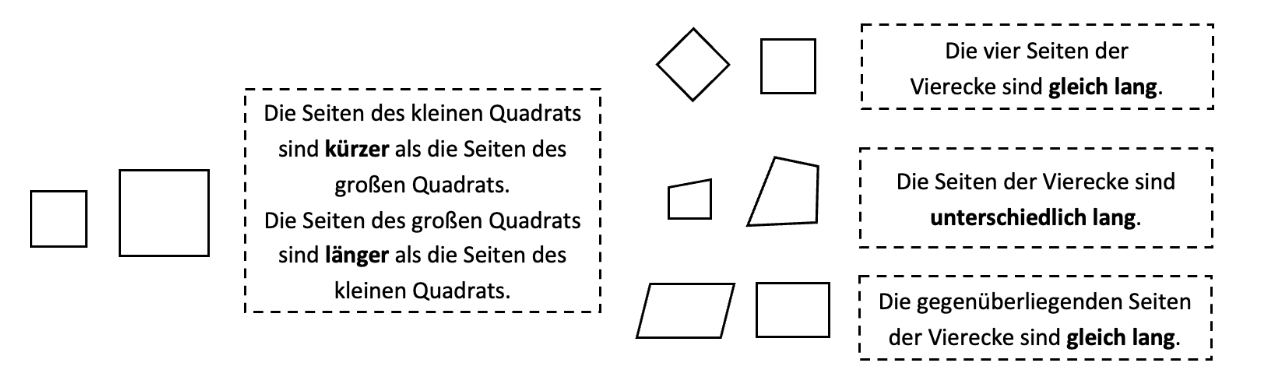
Abb. 5: Sprachspeicher: Vergleichen und Beschreiben von Relationen
Des Weiteren können Kinder beim Sortieren prüfen, ob sich Formen ähneln oder ob sie gleich sind. Sie können zwei oder mehrere Formen auf ihre Deckungsgleichheit, also ihre Kongruenz prüfen. Formen werden in der Geometrie als „deckungsgleich“ oder „kongruent“ beschrieben, wenn sie durch eine Bewegung (wie Verschieben, Drehen oder Spiegeln) exakt aufeinander abgebildet werden können. Das bedeutet, dass sie in Form und Größe identisch sind und alle Längen, Winkel und anderen geometrischen Eigenschaften bei dieser Abbildung unverändert bleiben.
Im Folgenden wollen wir einen kurzen Überblick über die geometrischen Formen Kreis, Dreieck, Viereck (und Vieleck) geben und bei der Beschreibung der Formeneigenschaften beispielhaft auf Lernanlässe beim Sortieren der jeweiligen Formen eingehen.
Der Kreis
Ein Kreis ist eine geometrische Form, die keine Ecken hat. Der Kreis ist rund und hat einen Mittelpunkt, der sich genau im Zentrum des Kreises befindet. Kreise können von Kindern aufgrund der runden Form ohne Ecken gut von anderen Formen unterschieden (Maier, 2019) und anschließend vor allem auf ihre unterschiedlichen Größen hin untersucht werden. Ziel bei Sortieraktivitäten in der Elementarstufe kann also zunächst das Identifizieren der Kreise und Unterscheiden der Kreise von Vielecken wie Dreiecken oder Vierecken sein. Schließlich können Kreise beim Sortieren insbesondere nach ihrer Größe sortiert werden (s. Abbildung 6).

Abb. 6: Kinder sortieren Kreise nach ihrer Größe
In der Abbildung sieht man zwei verschiedene Sortierungen von Kindern der Schuleingangsphase, die in Partnerarbeit Formen sortiert haben. Beide Kinderpaare haben alle Kreise identifiziert. Auf der linken Seite hat Lina nach kleinen, mittleren und großen Kreisen sortiert. Auf der rechten Seite geschieht die Sortierung der Kreise von Stephan bis auf eine Ausnahme rechts oben in der Reihenfolge der Größe. Die unterschiedliche Größenausprägung ist bei diesen Formen noch so deutlich, dass ein Vergleichen der unterschiedlich großen Formen für Kinder durch Beobachtung und das Übereinanderlegen der Formen möglich ist.
Das Dreieck
Ein Dreieck ist eine geometrische Form, die genau drei Ecken und drei Seiten hat. Die Identifikation eines Dreiecks über die Anzahl der Ecken und Seiten ist Kindern schon früh möglich. Nachfolgend finden Sie eine Übersicht über besondere Dreiecke und ihre Eigenschaften, nach denen Kinder sortieren können. Das hier an das „Haus der Vierecke“ (s. u.) angelehnte und skizzierte „Haus der Dreiecke“ stellt einen Überblick über die verschiedenen Dreiecke dar und zeigt, wie diese miteinander in Beziehung stehen.
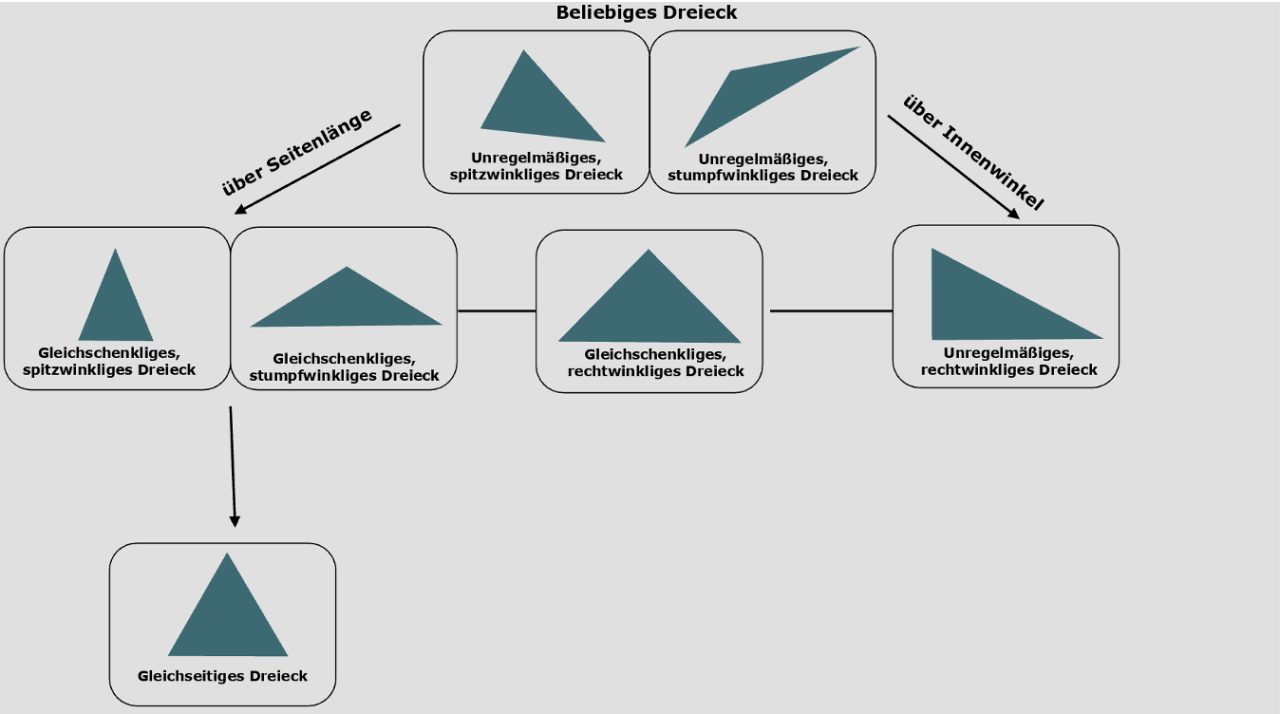 Abb. 7: „Das Haus der Dreiecke“
Abb. 7: „Das Haus der Dreiecke“
Die unterschiedlichen Dreiecke können insbesondere durch die Betrachtung der Innenwinkel und Seitenlängen unterschieden und somit kategorisiert werden.
-
Das „bekannteste“ Dreieck ist für die Kinder das gleichseitige Dreieck (Unterhauser, 2019, S. 238). Dort sind alle Seiten gleich lang und alle Innenwinkel sind gleich groß (60 Grad). Bei jedem spitzwinkligen Dreieck sind alle Innenwinkel kleiner als 90 Grad.
-
Beim gleichschenkligen Dreieck sind immer zwei Seiten gleich lang. Die beiden Winkel, die den gleich langen Seiten gegenüberliegen, sind gleich groß. Das gleichschenklige, stumpfwinklige Dreieck hat einen stumpfen Winkel, der größer als 90 Grad ist. Die anderen beiden Winkel müssen in Summe kleiner als 90 Grad sein.
-
Ein besonderes gleichschenkliges Dreieck ist das gleichschenklige, rechtwinklige Dreieck welches zu den oben beschriebenen Eigenschaften des gleichschenkligen, spitzwinkligen Dreiecks die Besonderheit aufweist, dass ein Winkel rechtwinklig ist.
-
Unregelmäßige Dreiecke haben unterschiedlich große Winkel und unterschiedlich lange Seitenlängen, sodass keine gleichen Schenkel vorliegen.
Dass es neben dem gleichseitigen Dreieck, welches für Kinder im Anfangsunterricht häufig als prototypisches Dreieck (Unterhauser, 2019, S. 453) wahrgenommen wird, auch viele weitere unterschiedliche Dreiecke gibt, können die Kinder beim Sortieren verschiedener Dreiecke erkunden. Auch wenn die fachsprachliche Beschreibung (z. B. gleichseitig, gleichschenklig, rechtwinklig, beliebig) der unterschiedlichen Dreiecke laut Lehrplänen erst in der Sekundarstufe I vorgesehen ist, können Kinder schon früh visuelle Unterschiede wahrnehmen und Flächeninhalte, Winkel und Kongruenzen durch Übereinander- und Nebeneinanderlegen der Formen erkunden - und nicht selten auch schon umschreiben und versprachlichen. Das Identifizieren von Dreiecken fällt Kindergartenkindern schwerer als das Identifizieren von Kreisen oder Quadraten (Maier, 2019, S. 107).
Zum Ende der Schuleingangsphase wird als Kompetenzerwartung das Identifizieren und fachsprachliche Beschreiben von Dreiecken unter der Nutzung der Begriffe Seite, Ecke und Fläche formuliert. Zudem sollen bei einfachen, ebenen Figuren Eigenschaften der Achsensymmetrie untersucht werden. Am Ende der vierten Klasse sollen ebenfalls rechte Winkel zur Beschreibung von Dreiecken genutzt, sowie Flächen und Umfänge bestimmt werden (MSW NRW, 2021). Die konkreten Bezeichnungen der verschiedenen Dreiecksarten nutzen Schülerinnen und Schüler dann in der Sekundarstufe I. (MSW NRW, 2019). Auch das explizite Berechnen der Flächeninhalte und Umfänge folgt gegen Ende der Sekundarstufe I beim rechtwinkligen Dreieck (MSW NRW, 2019), nachdem die Kinder in der Primarstufe zunächst „durch handelnden Umgang Grunderfahrungen zu Eigenschaften und Maßen von ebenen Figuren [...] (z. B. Umfang und Flächeninhalt)“ sammeln, z. B. durch das Auslegen mit Einheitsquadraten oder das Zerlegen von Formen in Teilstücke (MSW NRW, 2021). So muss es das Ziel sein, von Sortieraktivitäten hin zum Messen zu gelangen, mit dem dann eine Größenbestimmung über den Flächeninhalt möglich wird: „Für das Bestimmen von Flächen- und Rauminhalten muss gemessen werden. Denn oft genügt es nicht, Figuren oder Körper nach bestimmten Kriterien bzw. Eigenschaften zu vergleichen oder zu sortieren, sondern bestimmte ihrer Eigenschaften sollen durch Maße beschrieben werden“ (Kuntze, 2018, S. 150).
Die untenstehenden Beispiele (Abb. 8) zeigen, wie vielfältig die Kinder der Schuleingangsphase Dreiecke sortieren können, und dass sie dazu unterschiedliche Sortierkriterien zugrunde legen.

Abb. 8: Kinder sortieren unterschiedlich Dreiecke
Die Sortierungen umfassen unterschiedliche Vorgehensweisen: Anna sortiert gleichseitige Dreiecke in der Mitte, gleichschenklige und unregelmäßige Dreiecke auf der linken Seite und die größten Dreiecke auf der rechten Seite (1). Louis erstellt mit ausschließlich Dreiecken fantasievolle Figuren und nutzt spitzwinklige Dreiecke für die Flügel seiner Figuren (2). Pema identifiziert die zu sortierenden Dreiecke und separiert die gleichseitigen Dreiecke auf der rechten Seite (3) Dazu legt sie auch ein konkaves Viereck. Bente ordnet Dreiecke mit Blick auf ihre Größenverhältnisse und legt immer die längste Grundseite des Dreiecks nach unten (4). Paul legt alle nicht-gleichseitigen Dreiecke (und ein nicht als unterschiedlich identifizierte Raute) in seine Sortierung (5).
Das Viereck
Ein Viereck ist eine geometrische Form, die genau vier Ecken und vier Seiten hat. Die Identifikation eines Vierecks über die Anzahl der Ecken und Seiten ist für Kinder schon früh möglich. Die Veränderungen der Winkelgröße und Seitenlänge lassen vielfältige Vierecke entstehen. Auf Primakom finden Sie eine Übersicht zu Eigenschaften von Vierecken in Anlehnung an Breidenbachs (1964) Haus der Vierecke. In dem Haus der Vierecke werden verschiedene (besondere) Vierecke so angeordnet, dass die Beziehungen zwischen unterschiedlichen Vierecken visualisiert werden. Ausgehend von einem beliebigen Viereck werden weitere Eigenschaften wie z. B. die Veränderung der Innenwinkel oder der Parallelität des Vierecks so aufgeführt, dass eine Reihe besonderer Vierecke entstehen: das Quadrat, das Rechteck, die Raute, das Parallelogramm, das gleichschenklige Trapez, das Drachenviereck und das unregelmäßige Viereck.
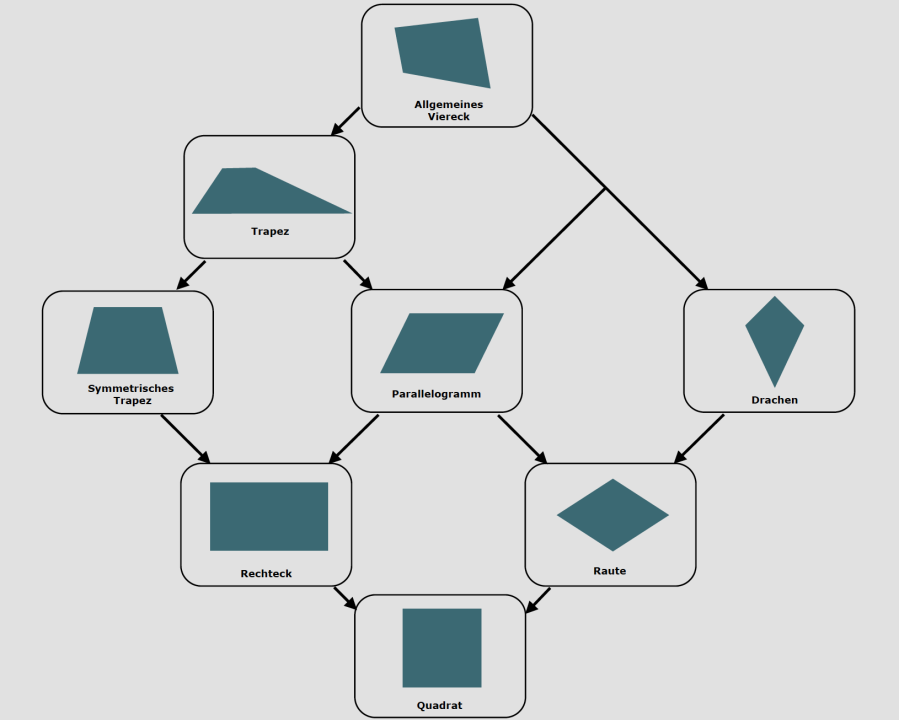 Abb. 9: Das Haus der Vierecke (in Anlehnung an Benz et al. 2015, S.186)
Abb. 9: Das Haus der Vierecke (in Anlehnung an Benz et al. 2015, S.186)
Ein weiteres besonderes Viereck, welches in der Aufgabenstellung kompakt seinen Einsatz findet und nicht im Haus der Vierecke abgebildet ist, ist das konkave Viereck. Bei einem konkaven Viereck weist ein Innenwinkel einen Wert größer als 180 Grad auf, während bei einem konvexen Viereck alle Innenwinkel kleiner als 180 Grad sind. Durch die Unterscheidung zwischen konvexen und konkaven Vierecken können die Eigenschaften und Beziehungen zwischen den Ecken bzw. Winkeln und Seiten eines Vierecks untersucht werden.
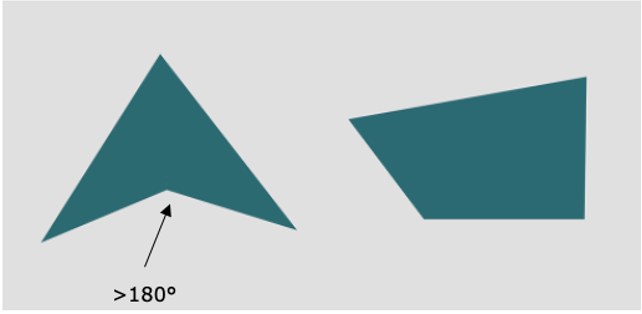
Abb. 10: konvexes Viereck (rechts): mind. ein Innenwinkel ist >180° und konkaves Viereck (links): alle Innenwinkel sind <180°
Die hier dargestellten Eigenschaften und Besonderheiten lassen sich durch gezielte Untersuchungen wie z. B. auch beim Sortieren erkunden. So können Kinder bspw. bei der Erkundung der Eigenschaften von Quadrat und Rechteck erkennen, dass auch ein Quadrat ein Rechteck (und ein Viereck) ist, mit den Besonderheiten, dass alle Seiten (und damit auch die sich gegenüberliegenden) und Diagonalen gleichlang sind, sich die Diagonalen gegenseitig halbieren und im Spezialfall des Quadrats im Gegensatz zum Rechteck auch senkrecht aufeinanderstehen.
Kinder können Vierecke auf vielfältige Art und Weise sortieren und identifizieren) (Abb. 11). zum Beispiel indem sie wie Caroline Rechtecke und Quadrate in zwei Kategorien aufteilen (1), wie Ann-Sophie Fantasiefiguren erschaffen, die nur aus Vierecken (aus fast ausschließlich Rechtecken, einem Trapez und einem Parallelogramm) bestehen (2), wie Stephan Quadrate nach ihrer Größe sortieren (3), wie Bente lange und schmale Rechtecke in eine Gruppe einteilen (4) oder wie Paul global alle Vierecke zusammenlegen und ähnliche Vierecke nebeneinander platzieren (z.B. oben links schmale Rechtecke, unten rechts Quadrate usw.) (5).

Abb. 11: Kinder sortieren verschiedene Vierecke
Beim Sortieren und Definieren von Vierecken verwenden Kindergartenkindern insbesondere den Begriff Viereck und weniger die Begriffe Rechteck oder Quadrat. Die Formen der Quadrate (ca. 80 %) und Rechtecke (ca. 75 %) können Kindergartenkinder schon häufig korrekt identifizieren. Das Identifizieren und Benennen weiterer Vierecke fällt hingegen schwer (Unterhauser, 2019, S. 244). Auch die Lage des Vierecks hat einen Einfluss auf die Identifikation durch die Kinder. So werden beispielsweise Quadrate, wenn diese um 45° gedreht werden, nicht mehr als Quadrate identifiziert (Unterhauser, 2019, S. 246).
Laut den Lehrplänen des Landes Nordrhein-Westfalen sollen Kinder in der Schuleingangsphase Quadrat und Rechteck identifizieren und mit Fachbegriffen (Seite, Ecke, Fläche) beschreiben lernen. Zudem sollen bei einfachen, ebenen Figuren Eigenschaften der Achsensymmetrie untersucht werden. Am Ende der vierten Klasse sollen weitere Vierecke wie u. a. das Parallelogramm identifiziert und fachsprachlich beschrieben werden (u. a. senkrecht, waagerecht, parallel, rechter Winkel) (MSW NRW, 2021). Weiterhin sollen Flächeninhalte der Vierecke und deren Umfang ermittelt und miteinander verglichen werden. Zu diesem Zweck werden Methoden wie das Auslegen mit Einheitsquadraten oder das Zerlegen in Teilstücke empfohlen.
In der Sekundarstufe I beschäftigen sich die Schülerinnen und Schüler in inhaltlichen Schwerpunkten schließlich mit „besondere[n] Vierecke[n]“ (MSW NRW, 2019). Die besonderen Vierecke sollen charakterisiert und klassifiziert werden (MSW NRW, 2019). Weitere Aspekte der Auseinandersetzung mit Vierecken sind: Winkel, Parallelität, Punktsymmetrie und Achsensymmetrie sowie die Berechnung von Umfang und Flächeninhalt von Rechtecken und die Bestimmung des Flächeninhalts weiterer ebener Figuren durch Zerlegungs- und Ergänzungsstrategien. Außerdem setzen sich die Lernenden mit Verschiebungen, Drehungen sowie Punkt- und Achsenspiegelungen von Abbildungen auseinander (MSW NRW, 2019).
Vielecke
Als weitere ebene Figuren können Vielecke ergänzend sortiert und auf ihre Eigenschaften hin untersucht werden. Vielecke haben wie auch Dreiecke und Vierecke immer die gleiche Anzahl an Ecken und Seiten. Aber auch die Symmetrieachsen können von den Kindern in den Blick genommen werden. Am Ende der Schuleingangsphase sollten die Schülerinnen und Schüler Sechsecke und Achtecke identifizieren und mit Fachbegriffen beschreiben (u. a. senkrecht, waagerecht, parallel, rechter Winkel) (MSW NRW, 2021).
Wenn Kinder Vielecke sortieren, können sie diese mit Blick auf die Anzahl der Ecken und Seiten kategorisieren, die Größe und ihre Regelmäßigkeit hin untersuchen.

Abb. 12: Fünfeck, Sechseck, Achteck