Digitale Zufallsgeneratoren, die auf Knopfdruck die Anzahl der Schritte ermitteln
Eine Möglichkeit ist ein digitaler Zufallsgenerator z.B. eine App, die mit einem einfachen Anklicken des Buttons betätigt werden kann.
Plus-Minus-Spiel
Abb. 1: Übersichtskarte Aufgabenstellung kompakt „Plus-Minus-Spiel“
Basisaufgabe
"Spielt das Plus-Minus-Spiel."
Material pro Kinderteam (2-3 Kinder)
- 1 Spielplan, 1 Spielfigur
- Würfel W12 für die Zahlen -5 bis + 5 (2x Null)
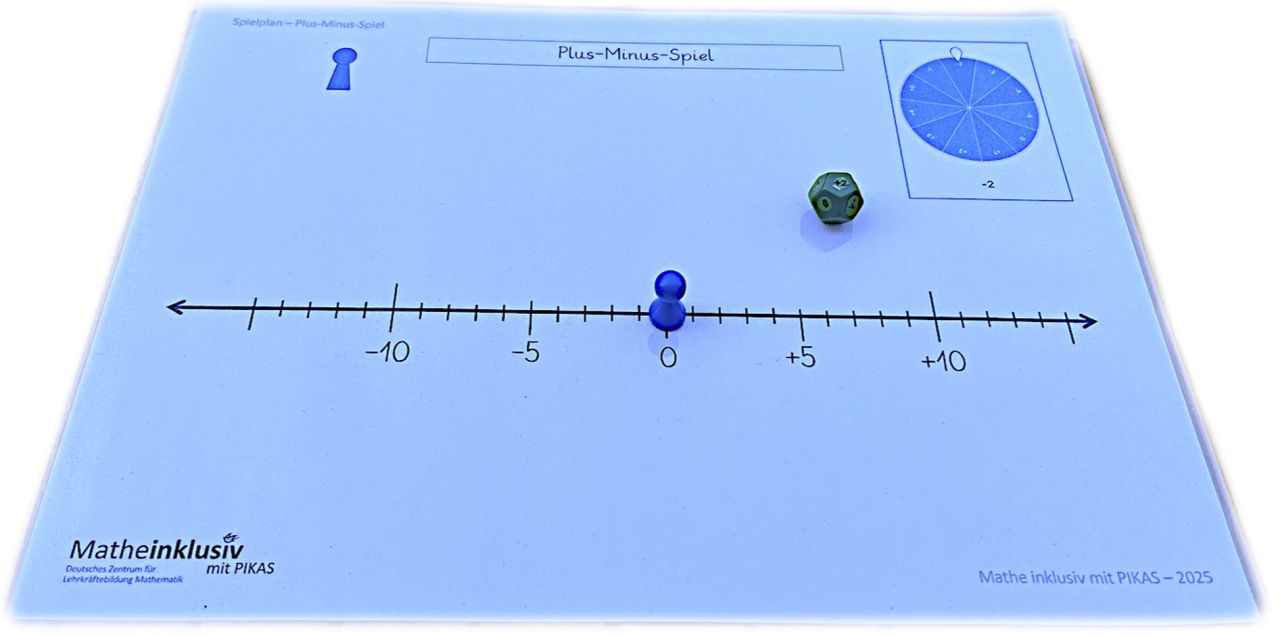
Ziel der Basisaufgabe
Ein Ziel dieser Basisaufgabe ist die Wiederholung und Verinnerlichung der Zahlengeraden (als Erweiterung des Zahlenstrahls) und somit der ordinale Zahlaspekt, hier speziell im Zahlenraum der ganzen Zahlen (anknüpfend an die Aufgabenstellung kompakt „Zahlen ordnen mit ganzen Zahlen“). Ein weiteres Ziel ist die Verdeutlichung von negativen Zahlen als Schritte in eine bestimmte Richtung (immer weiter nach links). Durch die Bewegung auf der Zahlengeraden wird dieser Aspekt handelnd erfahren und ermöglicht so eine intensive Auseinandersetzung mit dem Zahlenraum.
Spielregeln
- Ziel: Kommt gemeinsam zur kleinsten (-10) oder größten Zahl (+10) auf der Zahlengeraden.
- Die Spielfigur beginnt bei Null. Es wird abwechselnd gewürfelt.
- Bei einer negativen Schrittzahl wird die Spielfigur in Richtung -10 bewegt, bei einer positiven Schrittzahl in Richtung +10.
- Wird die Spielfigur auf die -10 oder die +10 (oder darüber hinaus) gezogen, habt ihr gewonnen und das Spiel endet.
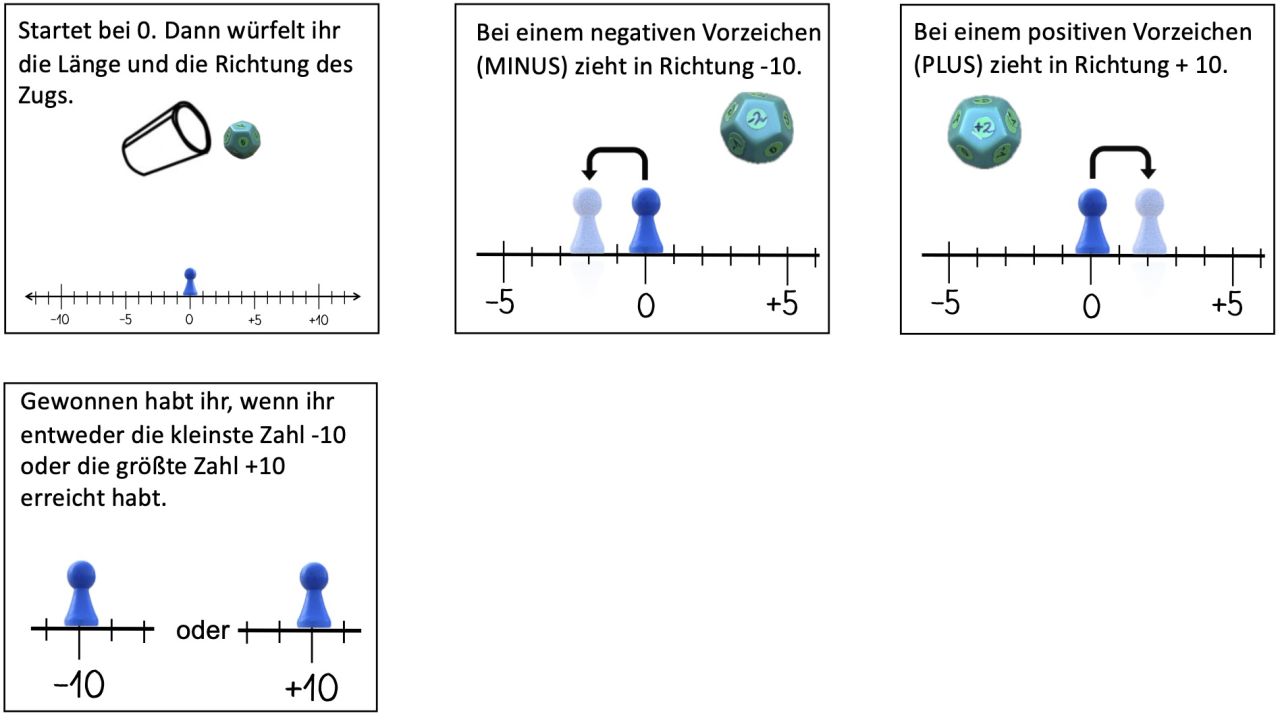
Abb.3: Basisregeln „Plus-Minus-Spiel“ (können durch weitere Regelkarten bei Bedarf ergänzt oder variiert werden)
Die Spielregeln können je nach Einsatz im Unterricht individuell angepasst und zusammengesetzt werden. Dafür gibt es eine Auswahl an unterschiedlichen Varianten von Regelkarten, die bei Bedarf auch selbst noch ergänzt werden kann (hier finden sie diese Varianten als Kartensatz der Regelkarten zum Ausdrucken und/oder Selbstzusammenstellen).
Weiter hinten befinden sich Ausführungen zu möglichen unterrichtlichen Einstiegen des Plus-Minus-Spiels sowie Ideen zur Reflexion und Weiterarbeit.
Bei der Durchführung des Basisspiels ist zu beachten, dass folgende Aufgabenformate erarbeitet und thematisiert werden können:
(+X) + (+Y)
(-X) + (+Y)
(+X) + (-Y)
(-X) + (-Y)
Es können demnach alle Additionsaufgaben mit ganzen Zahlen, jedoch keine Subtraktionsaufgaben mit negativen Zahlen abgebildet werden (z.B. – (-4)).
Um den Unterschied zwischen positiven und negativen Zahlen hervorzuheben, setzen wir bewusst Pluszeichen vor die positiven Zahlen. Grundsätzlich können diese im Unterricht auch weggelassen werden, sofern der Unterschied zwischen positiven und negativen Zahlen von den Schülerinnen und Schülern verstanden ist.
Mögliche Basisaktivität und Umsetzung – „Notiert euren Zug.“
„Spielt das Plus-Minus-Spiel und notiert nach jedem Wurf euren Zug in der Tabelle.“
Material pro Kinderteam (2-3 Kinder)
- 1 Spielplan, 1 Spielfigur
- Würfel W12 für die Zahlen -5 bis + 5 (2x Null)
- Notationstabellen „Notiert euren Zug.“
Abb.4: Notationstabelle und Spielplan mit Material für das Basisspiel
Die Schülerinnen und Schüler spielen das Basisspiel und tragen alle durchgeführten Züge in eine Notationstabelle ein. Sollte eine Tabelle komplett ausgefüllt sein, kann das Spiel in einer zweiten Notationstabelle fortgesetzt werden.
Die Notation der Züge hat im Kontext des Spiels drei Funktionen. Zum einen dient sie dazu, am Ende die Anzahl der benötigten Züge zu ermitteln und so „Bestspiele“ herauszustellen. Mathematisch gesehen, ist sie zudem die Vorbereitung auf das Rechnen mit ganzen Zahlen. Zusätzlich werden durch die Notation der Spielzüge zwei Darstellungsebenen miteinander verknüpft: die Ebene der Handlungen am Material mit der Ebene der mathematischen Symbole.
Didaktische Variation
„Spielt das Plus-Minus-Spiel. Wenn ihr mit 10 oder weniger Zügen zum Ziel (-10 oder +10) kommt, habt ihr gewonnen. Notiert dafür eure Spielzüge in der Tabelle.“
Je nachdem, welche Zahlen gewürfelt werden, kann das Spiel „unendlich“ lang dauern. Um eine zeitliche Kalkulation der Spielzeit besser zu ermöglichen, kann das Spiel nach 10 Zügen (eine volle Notationskarte) beendet werden. Zu beachten ist, dass durch diese Variante die Erfahrung unterbunden wird, dass es sehr lange (bis „unendliche“) Spiele geben kann.
Mögliche Basisaktivität und Umsetzung – „Zeichnet euren Schritt als Pfeil.“
„Spielt das Plus-Minus-Spiel und zeichnet nach jedem Wurf euren Schritt als Pfeil an der Zahlengeraden ein.“
Material pro Kinderpaar
- Ggf. 1 Spielplan + 1 Spielfigur
- Würfel W12 für die Zahlen -5 bis + 5 (2x Null)
- Notationskarten „Zeichnet euren Schritt als Pfeil.“
Abb. 5: Ausschnitt Notationstabelle“ Notiert euren Zug.“ und ausgefüllte Notationskarte „Zeichnet euren Schritt als Pfeil.“ – Basis
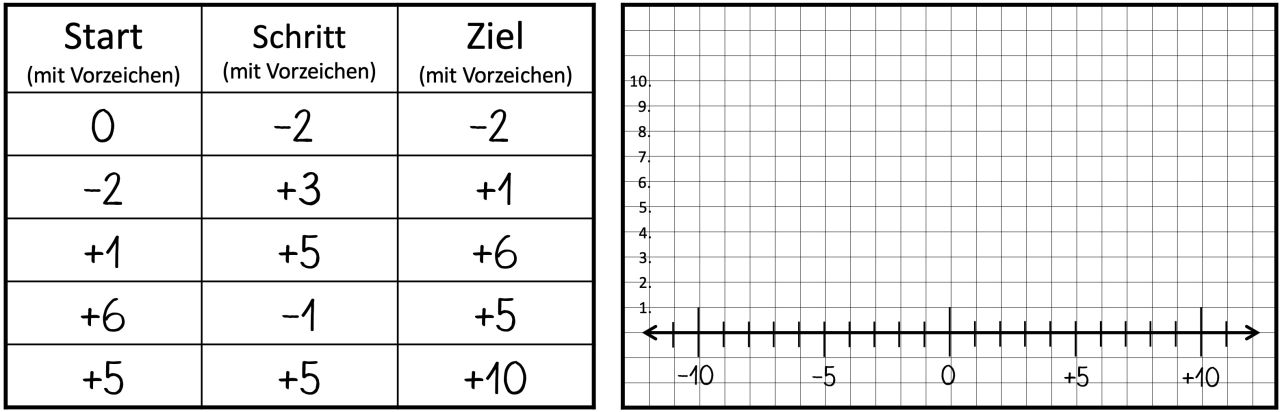
Abb. 6: Notationstabelle „Notiert euren Zug.“ und leere Pfeilkarte „Zeichnet euren Schritt als Pfeil.“ – mögliche Erweiterung
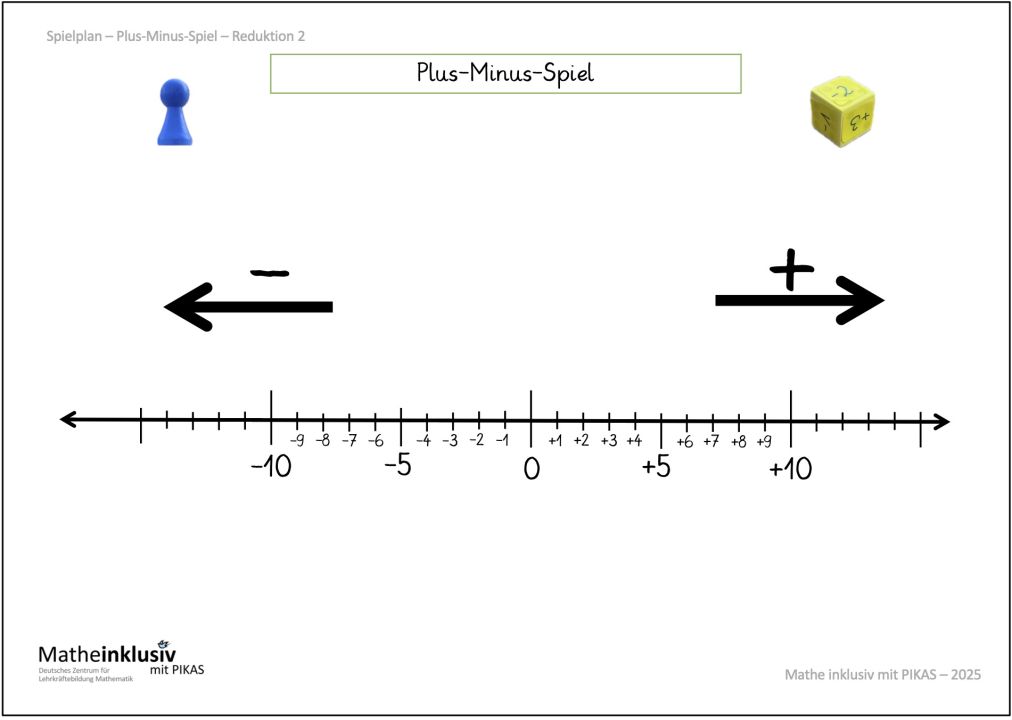
Mit dieser Basisaktivität wird durch den geforderten Darstellungswechsel die Vorstellung von ganzen Zahlen als Schritt mit unterschiedlicher Länge (je nach Vorzeichen in Richtung Minus oder Plus) auf der Zahlengeraden hervorgehoben und durch die Pfeile visuell verdeutlicht.
Beim Einsatz der erweiterten Pfeilkarte der Basisaktivität ist wichtig mit den Schülerinnen und Schülern zu thematisieren, dass die Notationstabelle von oben nach unten eingetragen wird, während die Pfeile auf der Pfeilkarte andersherum von unten nach oben eingetragen werden.
Diese Basisaktivität erfordert und übt neben dem mathematischen Darstellungswechsel die Fähigkeit, sauber und präzise zu zeichnen und ist mit allen Reduktionen und Erweiterungen einsetzbar.
Mögliche Reduktion - Beschriftung Zahlengerade
Wenn Kinder noch unsicher bei der Orientierung auf der Zahlengeraden sind, ist eine gute Möglichkeit der Reduktion, die mit allen Vertiefungen verbunden werden kann, die Zahlengerade nicht nur in 5er-Schritten, sondern in Einerschritten zu beschriften. So gelingt eine schnellere Orientierung während des Spiels.
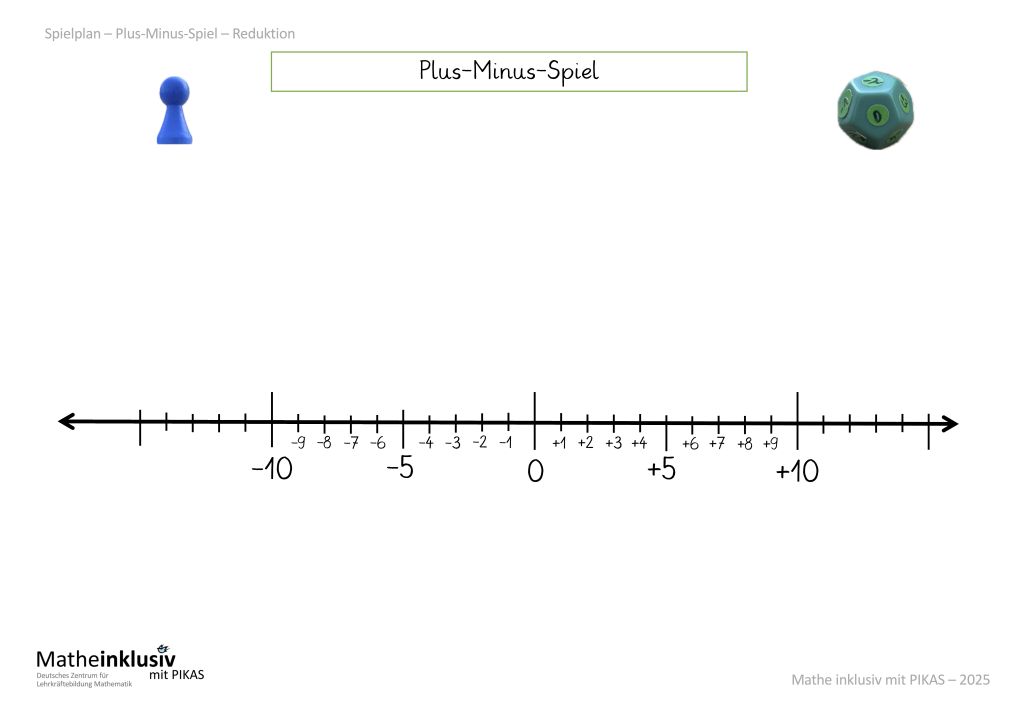
Abb. 7: Spielplan: mögliche Reduktion - Beschriftung Zahlengerade
Mögliche Reduktion - Verkleinerung des Zahlenraums
Zahlenraum Zahlengerade/Zufallsgenerator
Eine wirksame Reduktion, die mit allen Basisaktivitäten verbunden werden kann, ist die Verkleinerung des genutzten Zahlenraums der Zahlengeraden. Damit das Spiel dann nicht zu schnell beendet ist, sollte auch der Zufallsgenerator entsprechend angepasst werden:
- Zahlengerade nur von -5 bis + 5; Zufallsgenerator mit minimiertem Zahlenraum (z.B. -2 bis +2)
-
Zufallsgenerator nur mit -1, 0 und +1;
- -1 bedeutet einen Schritt in Richtung MINUS, +1 bedeutet einen Schritt in Richtung PLUS und Null bedeutet „Keinen Schritt gehen.“
Mögliche Erweiterung - Vergrößerung des Zahlenraums
Zahlenraum Zahlengerade/Zufallsgenerator
Der Zahlenraum des Spielfelds kann für leistungsstarke Kinder erweitert werden. Damit das Spiel dann nicht allzu lang dauert, ist es wichtig, auch den Zufallsgenerator entsprechend anzupassen. Interessant kann dabei auch eine Anpassung in 2er-Schritten sein. Alle diese Veränderungen sind mit den Basisaktivitäten nutzbar.
- Spielfeld von -40 bis +40
-
zusätzlich veränderterer Zufallsgenerator z.B.
- Würfel W20 von -10 bis +10 (ohne Null)
- digitaler Zufallsgenerator von -10 bis +10 (mit Null)
- Würfel W12 mit geraden Zahlen von -2 bis +10 (-2, -4, -6….) (2x Null)
Mögliche Erweiterung - Zahlenraum
Zehnerzahlen
Eine weitere Möglichkeit der Erweiterung ist die Nutzung von Zehnerzahlen. Wichtig ist dabei zu beachten, dass die Kinder, die mit dieser Erweiterung spielen, das Prinzip der Zehnerzahlen sicher beherrschen. So können die Erkenntnisse zu den Zehnerzahlen parallel vertieft werden. Auch diese Erweiterung kann mit allen Basisaktivitäten verbunden werden.
Nach einem ersten Kennenlernen des Spiels, Spielfeld von -150 bis +150 und in Zehnerschritten spielen: 1 = 10, 2 = 20 etc.
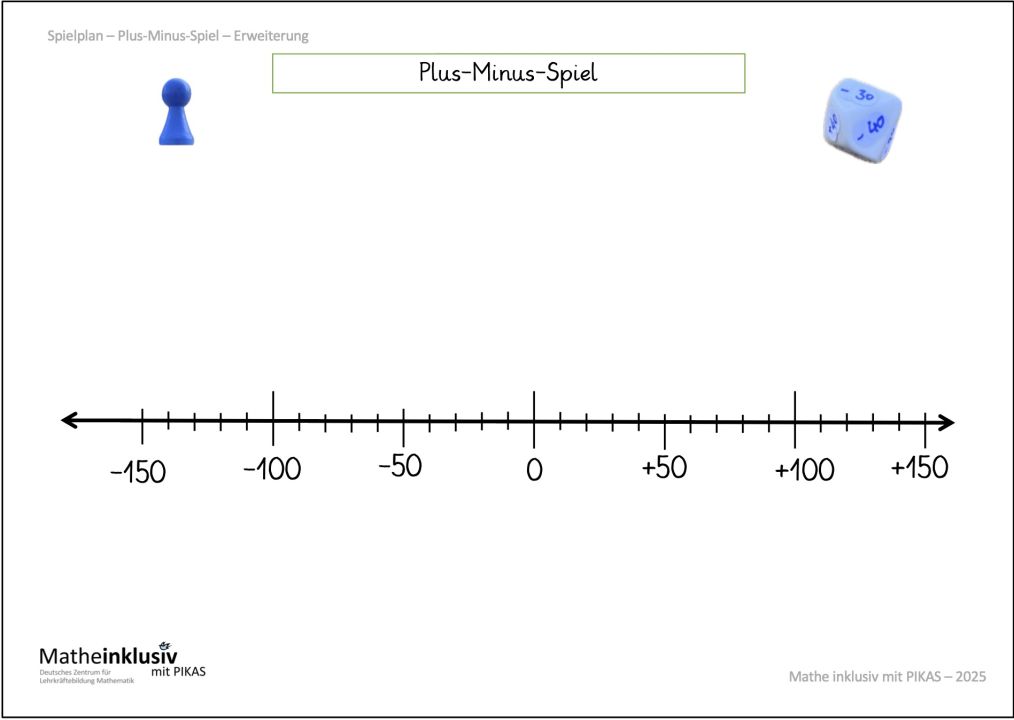
Abb. 8: Spielplan: mögliche Erweiterung – Zahlenraum Zehnerzahlen
Möglichkeiten individueller Unterstützung - Zufallsgenerator
Je nach motorischen Fähigkeiten der Kinder können bei starken Einschränkungen Zufallsgeneratoren genutzt werden, die mit einem einfachen Knopfdruck betätigt werden:
All-Turn-It-Spinner als Zufallsgenerator (UK)
Auch ein All-Turn-it-Spinner aus dem Bereich der Unterstützten Kommunikation kann mit einem individuellen Deckblatt (z.B. mit den Zahlen -3 bis +3) für das Ermitteln der Schrittanzahl genutzt werden.
Mit Flüsterwürfeln in einen Spieledeckel würfeln
Um den Geräuschpegel beim Würfeln zu minimieren, kann der Einsatz von angepassten Flüsterwürfeln (Zahlenraum -3 bis +3) aus weichem Schaumstoff sinnvoll sein.
Möglichkeiten individueller Unterstützung - Anpassung Spielfeld
Um Kinder mit feinmotorischen Einschränkungen am Spiel zu beteiligen kann das Spielfeld variiert werden.
Spielfeld auf dem Boden und selbst die Spielfigur sein oder mit einer großen Spielfigur ziehen
Die Kinder können auf dem mit Kreppband aufgeklebten Spielfeld entweder selbst die Spielfigur sein und die ermittelten Schritte direkt nachvollziehen oder mit einer großen Spielfigur (hier Plastikflasche) ziehen. Diese Variante kann auch für den Einstieg mit der gesamten Lerngruppe genutzt werden.
Spielfeld mit Krepp auf dem Tisch aufkleben und eine stabile bzw. standfeste Figur nutzen
Je nach motorischen Fähigkeiten kann ein Spielfeld auf dem Tisch mit Krepp aufgeklebt werden und ein Gegenstand als Spielfigur ausgewählt werden, der für die jeweiligen Kinder gut zu greifen und zu halten ist. Durch das aufgeklebte Spielfeld wird verhindert, dass bei unwillkürlichen Bewegungen das Spielfeld verrutschen oder herunterfallen kann. Besonders für Kinder im Förderschwerpunkt Körperliche und motorische Entwicklung kann so eine mathematisch gleichwertige Teilhabe ermöglicht werden.
Spielfeld mit deutlich visuell hervorgehobener „Plus- und Minusrichtung“
Mögliche Anschlusssequenz – „Was sind die wenigsten Züge?“
„Findet Wege, mit möglichst wenigen Zügen zu gewinnen. Schreibt diese auf.“
„Was ist die Möglichkeit mit den wenigsten Zügen? Findet alle Möglichkeiten.“
Ziel der Anschlusssequenz
Ziel ist es, das Spielprinzip ein Stück von dem konkreten Spiel zu lösen und die Mathematik dahinter zu untersuchen. Zudem können die angeregten Überlegungen auf unterschiedliche Zahlenräume von Zufallsgeneratoren und Spielfeldern übertragen werden bzw. die eingesetzten Zufallsgeneratoren und Spielfeldern mit ihren jeweiligen Zahlenräumen miteinander verbunden werden. Somit wird diese Anschlusssequenz für alle Reduktionen und Erweiterungen wertvoll.
Die Anschlusssequenz bildet die Grundlage für die Reflexion „Was sind die wenigsten Züge?“, die auch direkt als Reflexionsphase für die Basisaufgabe eingesetzt werden kann. Ist dieses Vorgehen geplant, ist es sinnvoll die Basisaktivität „Notiert euren Zug.“ parallel zur Basisaufgabe durchzuführen.
Mögliche Anschlusssequenz – „Auf welcher Zahl landet die Spielfigur?“
„Spielt das Plus-Minus-Spiel. Überlegt, bevor ihr zieht, wo die Spielfigur landet. Schreibt das Ergebnis auf und überprüft dann eure Überlegung durch Ziehen.“
Material
- 1 Spielplan, 1 Spielfigur
- Würfel W12 für die Zahlen -5 bis + 5 (2x Null)
- ggf. Notationstabellen aus der Basisaktivität "Notiert euren Zug."
- ggf. Arbeitsblatt "Auf welcher Zahl landet die Spielfigur?"
Anmerkung
Für die Anschlusssequenz ist es sinnvoll, die Basisaufgabe mit der Basisaktivität „Notiert euren Zug.“ zu kombinieren.
Ziel der Anschlusssequenz
Bei dieser Anschlusssequenz geht es um die Anbahnung der mathematischen Operation, die durch das Ziehen der Spielfigur repräsentiert wird. Die Schülerinnen und Schüler sollen das Zielfeld anhand der Startzahl sowie anhand Länge und Richtung des Schritts direkt ermitteln, ohne dies auf dem Spielfeld abzulaufen. Das Spielfeld kann als Lösungskontrolle genutzt werden. Die mathematische Veränderung um den Schritt (entweder in den positiven oder den negativen Bereich) wird so direkt mit der Zahlengeraden als inneres Bild verknüpft. Gelingt diese Verknüpfung, stellt sie eine tragfähige mathematische Vorstellung für das Addieren von ganzen Zahlen dar.
Die grundsätzlichen Fragenstellungen dieser Anschlusssequenz können auf alle Reduktionen und Erweiterungen angewendet werden. Es sollten dann die Aufgabenblätter hinsichtlich des eingesetzten Zahlraums entsprechend angepasst werden.
Impulse für eine mögliche Reflexion
- „Mit welchen Schritten konntet ihr die Zielzahl besonders schnell finden?“
- „Bei welchen Schritten habt ihr lange nachgedacht?“
- „Bei welchen Schritten habt ihr das Spielfeld gebraucht, um die richtige Zielzahl zu finden?“
- „Was war der einfachste/schwierigste Schritt?“
- „Gab es Unterschiede zwischen positiven und negativen Zahlen?“
Abb. 9: Mögliche Anschlusssequenz – „Auf welcher Zahl landet die Spielfigur?“ Arbeitsblatt Basisaufgabe
Reduktion
Zu Beginn können die Schülerinnen und Schüler zur Unterstützung einen Spielplan nutzen, damit sie die Schritte am Zahlenstrahl noch einmal konkret nachvollziehen können.
Zudem kann für leistungsschwache Kinder der Zahlenraum des Arbeitsblatts entsprechend der Reduktion (Zufallsgenerator von -2 bis +2) verringert werden (vgl. Arbeitsblatt „Auf welcher Zahl landet die Spielfigur?“ – Reduktion). Dadurch, dass die Schritte eine kurze Länge haben, wird die Vorstellung der Schritte an einem imaginären Zahlenstrahl vereinfacht.
Erweiterung
Für leistungsstarke Kinder kann diese Aufgabe erweitert werden, in dem diese die Zielzahl nach zwei Schritten lösen. Hier sind die unterschiedlichen Herangehensweisen (z.B. jeden Schritt nacheinander ermitteln oder erst die beiden Schritte miteinander verrechnen und dann die Zielzahl ermitteln) interessant und die Kinder sollen diese zusätzlich notieren.
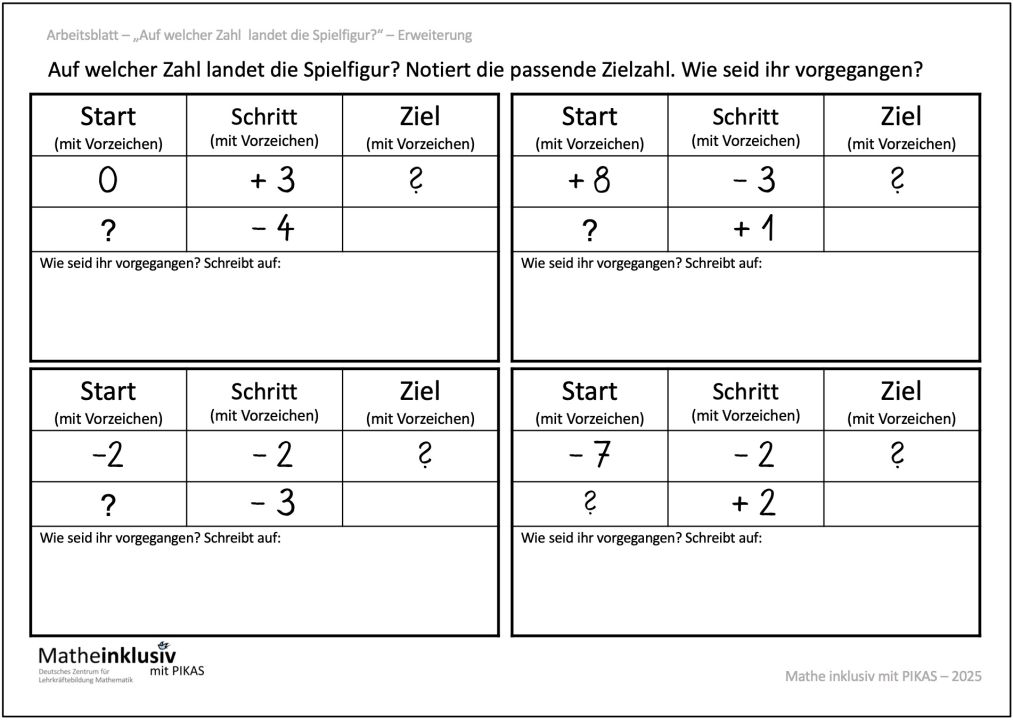
Abb. 10: Mögliche Anschlusssequenz – „Auf welcher Zahl landet die Spielfigur?“ Arbeitsblatt Erweiterung
Variante
Die Kinder decken bei der Ermittlung der Schritte das Spielfeld ab, um wirklich ohne Blick auf die Zahlengerade die Zielzahl zu ermitteln und somit die Ansprache, der inneren Repräsentation der Zahlengeraden zu verstärken.
Mögliche Einstiege
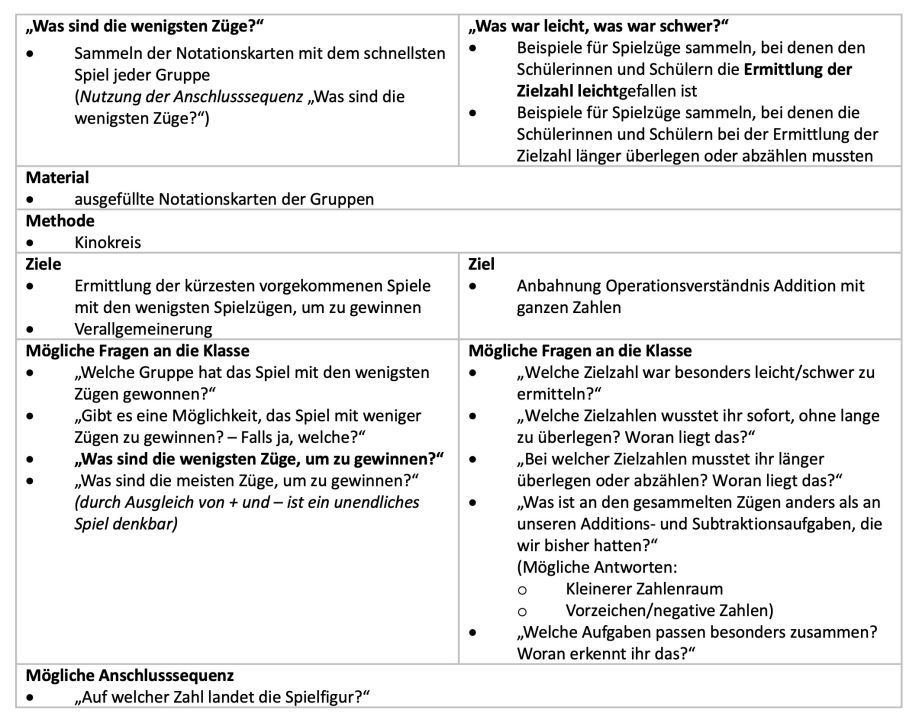
Hier finden sie Möglichkeiten der Einführung des Plus-Minus-Spiel in seiner Basisaufgabe "Spielt das Plus-Minus-Spiel." Neben den möglichen Präsentationen (Zahlengerade auf dem Boden oder an der (digitalen) Tafel) und dem Material, finden Sie auch Zielformulierungen sowie mögliche Fragen an die Klasse, um diese zum Mitdenken und Verstehen anzuregen.
Mögliche Reflexionen
Die hier dargestellten exemplarischen Reflexionen bauen auf eine Unterrichtseinheit auf, die sowohl die Einführung und Durchführung der Basisaufgabe zum Plus-Minus-Spiel sowie die Basisaktivität "Notiert euren Zug." beinhaltet. Es werden zwei Schwerpunktsetzungen vorgeschlagen, mit denen die durchgeführten Aktivitäten jeweils reflektiert werden können. In der Tabelle werden die möglichen Ziele, exemplarische Fragen an die Klasse sowie mögliche Weiterführungen zu den beiden exemplarischen Schwerpunktsetzungen vorgestellt.
