Vorgegebene Zahl 6:
"Finde Aufgabenfamilien: Immer zwei Mal- und zwei Geteiltaufgaben!"
Aufgabenstellung kompakt "Aufgabenfamilien"
Basisaufgabe
"Immer vier Aufgaben"
Material: AB, Stift
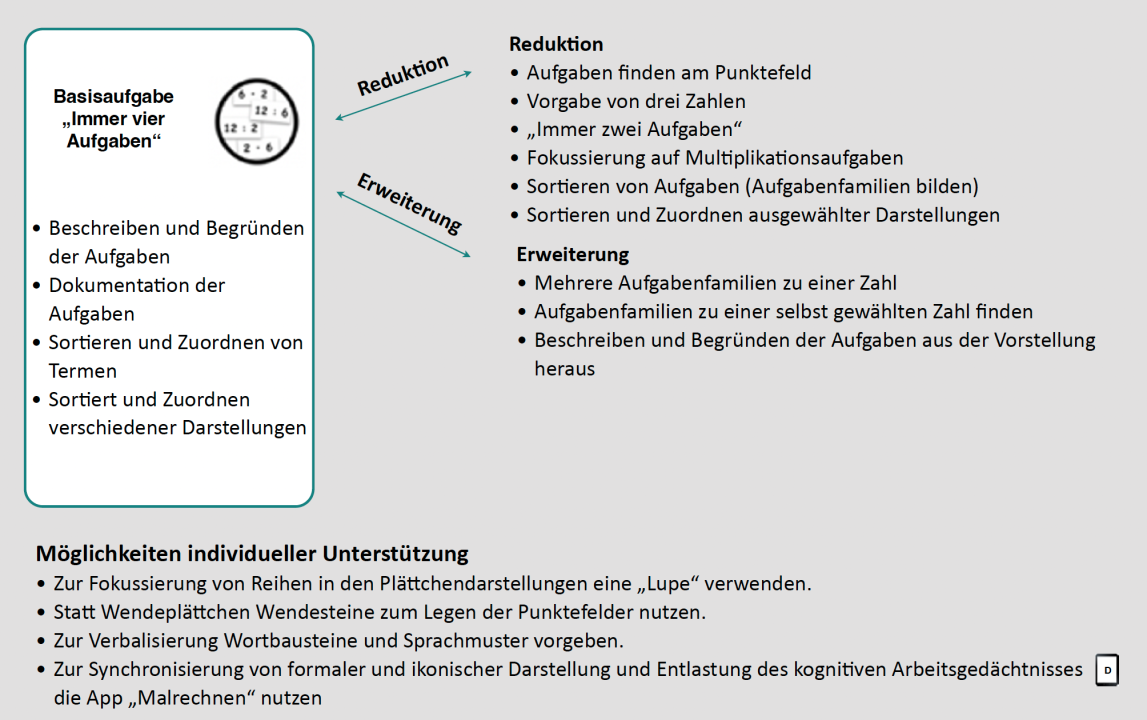
Grundlegend geht es bei dieser Aufgabenstellung um das Erkennen und Nutzen von Beziehungen zwischen Aufgabe, Tauschaufgabe und den zugehörigen Umkehraufgaben.
Zu einer vorgegebenen Zahl sollen immer vier Aufgaben notiert werden: zwei Malaufgaben und zwei Geteiltaufgaben.
Geklärt werden muss vor der Bearbeitung der Aufgabenstellung, dass es um die Notation von "Aufgabenfamilien" geht, d.h. gesucht ist immer eine Aufgabe, die zugehörige Tauschaufgabe und die jeweiligen Umkehraufgaben.
Nicht vorgegeben wird die "Position" der Zahl in der Aufgabe, d.h. so kann die Zahl in einer Multiplikationsaufgabe beispielsweise als Ergebniszahl, Multiplikand oder Multiplikator auftreten. Hierdurch ergibt sich die Möglichkeit, dass zu einer vorgegebenen Zahl unterschiedliche "Aufgabenfamilien" notiert werden (vgl. hierzu auch Erweiterung "Verschiedene Aufgabenfamilien zu einer Zahl").
Wichtig:
Im Vorfeld
- Mal- und Geteiltaufgaben zu Rechteckdarstellungen finden lassen
- Beziehungen zwischen Multiplikation und Division über Aufgaben und Umkehraufgaben herausstellen
- Sichern der Begriffe Aufgabe, Umkehraufgabe, Tauschaufgabe
- Klären, dass immer eine Aufgabe, die zugehörige Tauschaufgabe und die jeweiligen Umkehraufgaben gesucht sind ("Aufgabenfamilie")
Beispiele für mögliche Aufgabenfamilien zu der Zahl 6:
Basisaktivität
Beschreiben und Begründen der Aufgaben
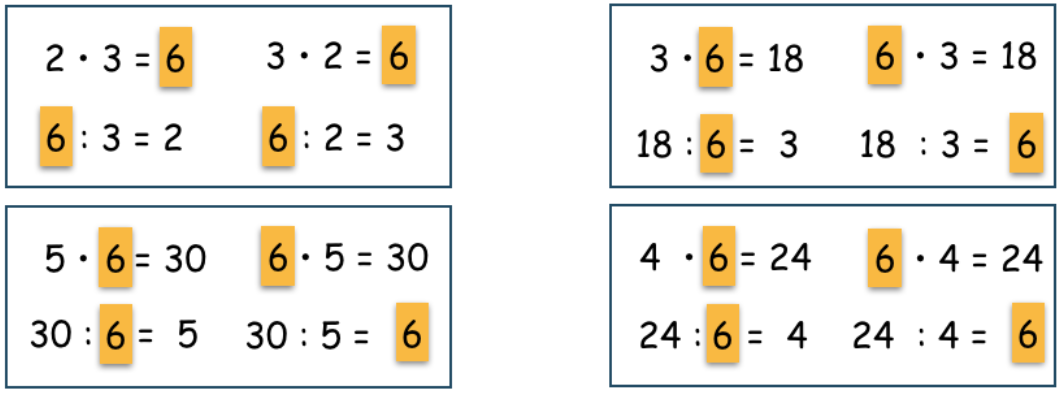
Material: AB, Stift
Da die Aufgabe in Einzelarbeit bearbeitet wird, erfolgt das Beschreiben und Begründen der Aufgaben ausschließlich schriftlich. Möglichkeiten der Versprachlichung werden unter: "Basisaktivität - Dokumentation der Aufgaben" ausführlich dargestellt.
Basisaktivität
Dokumentation der Aufgaben
Material: AB, Stift
Neben der Notation der Aufgaben in symbolischer Form kann zusätzlich eine ausführlichere Form der Dokumentation angeregt werden. Hierdurch wird von den Kindern zusätzlich ein Darstellungswechsel eingefordert.
Beispiele für eine ausführlichere Dokumentation am Beispiel einer Aufgabenfamilie zur Zahl 6:
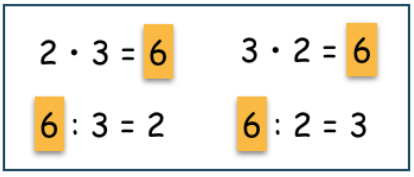
Legen oder Zeichnen eines passenden Punktefeldes.
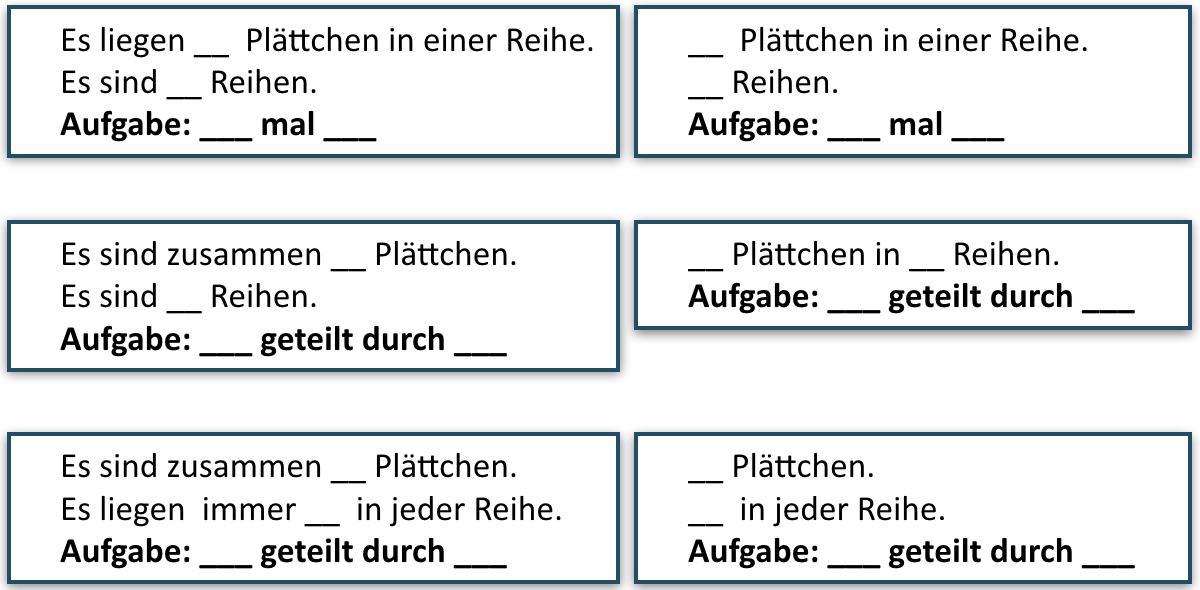
Beschreiben und Begründen (mögliche Versprachlichung):
Die Kinder formulieren nach dem Legen bzw. Zeichnen eines passenden Punktefeldes selbständig oder ergänzen vorgegebene Sätze.
Basisaktivität
Sortieren und Zuordnen von Termen
Material: Sortiertafel, vorgegebene Aufgaben
Die Kinder erhalten Karten mit verschiedenen Mal- und Geteiltaufgaben. Auf einer Sortiertafel werden die vier Aufgaben, die zu einer Aufgabenfamilie gehören, einander zugeordnet. Um eine passende Zuordnung treffen zu können, müssen die Ergebnisse von den Kindern ermittelt werden.
Basisaktivität
Sortieren und Zuordnen verschiedener Darstellungen
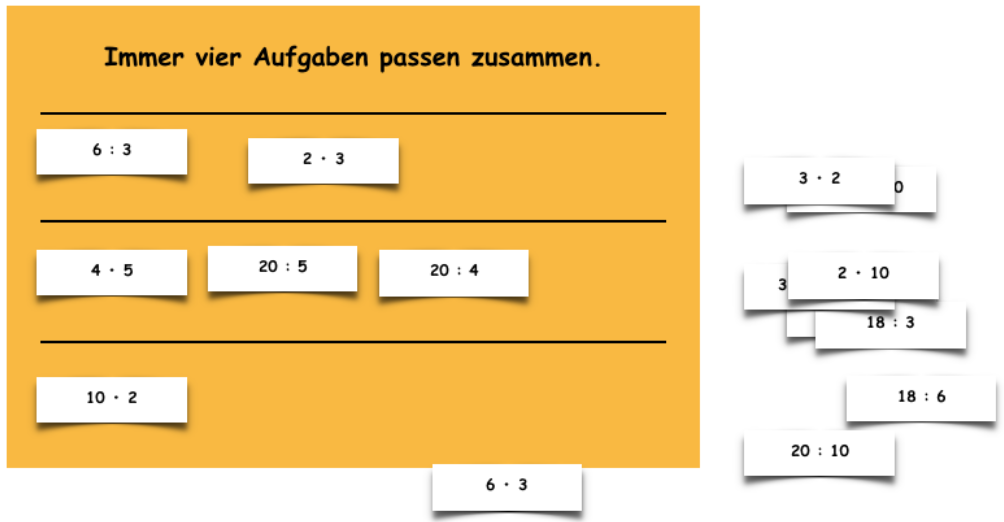
Material: Sortiertafel, Karten mit verschiedenen Darstellungen
Die Kinder erhalten Karten mit verschiedenen Darstellungen von Mal- und Geteiltaufgaben und ordnen auf einer Sortiertafel passende Darstellungen einander zu. Der Fokus liegt hier auf der Verknüpfung bzw. Zuordnung von Darstellungen einer Darstellungsform bzw. zwischen verschiedenen Darstellungsformen.
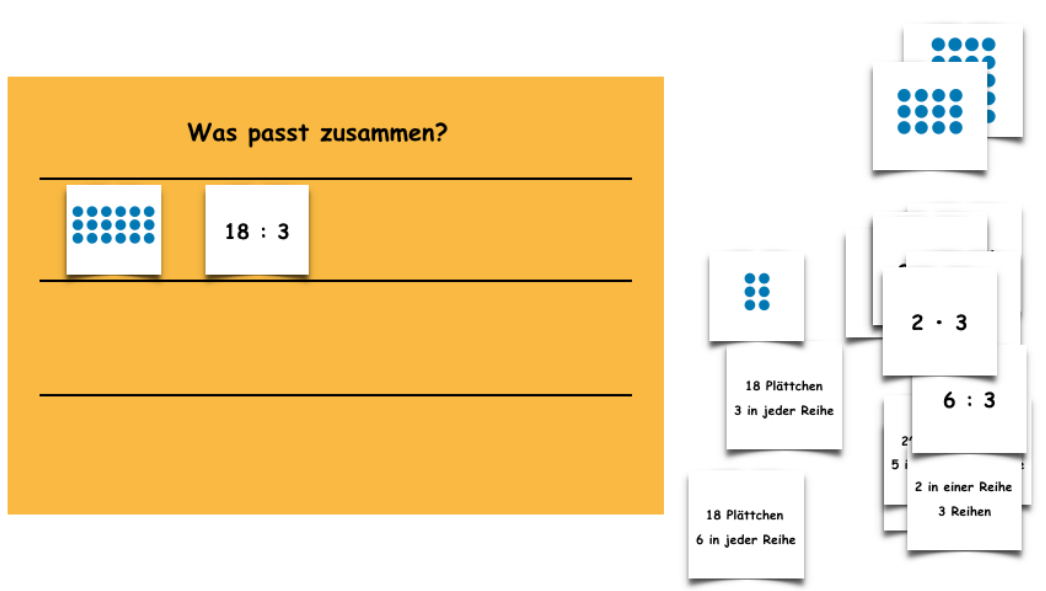
Wichtig: Aufgrund der Mehrdeutigkeit von einzelnen Darstellungen kann es zu unterschiedlichen Sortierungen kommen.
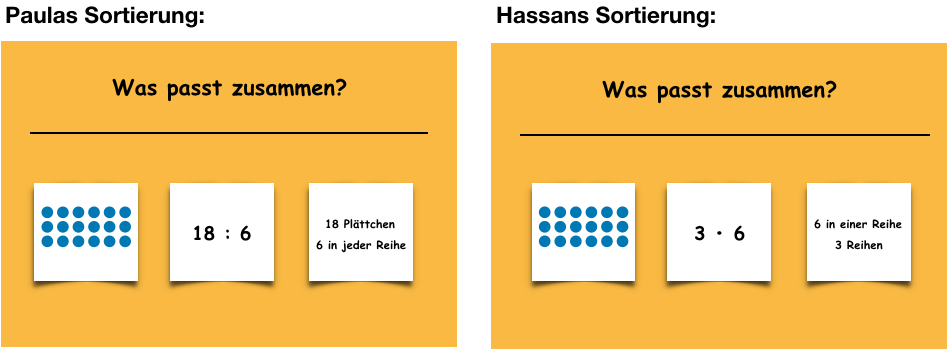
Ein Vergleich solch unterschiedlicher Sortierungen bietet in einer sich anschließenden Reflexionsphase eine gute Gesprächs- und Diskussionsgrundlage.
Reduktion
Aufgaben finden am Punktefeld
Material: Wendeplättchen, Darstellungen von Punktefeldern, AB, Stift
Das Arbeiten auf der rein symbolischen Ebene (vgl. Basisaufgabe "Immer vier Aufgaben") wird zurückgestellt. Die Kinder erhalten neben der vorgegebenen Zahl ein Punktefeld, das zu dieser Zahl passt (Die Zahl stellt entweder die Gesamtzahl der Punkte oder die Anzahl der Punkte in einer Spalte oder Reihe dar). Das Finden von Aufgaben kann durch das Einbeziehen des Punktefeldes unterstützt werden.
Beispiel "Zahl und Punktefeld":
Beispiel für eine mögliche Notation:
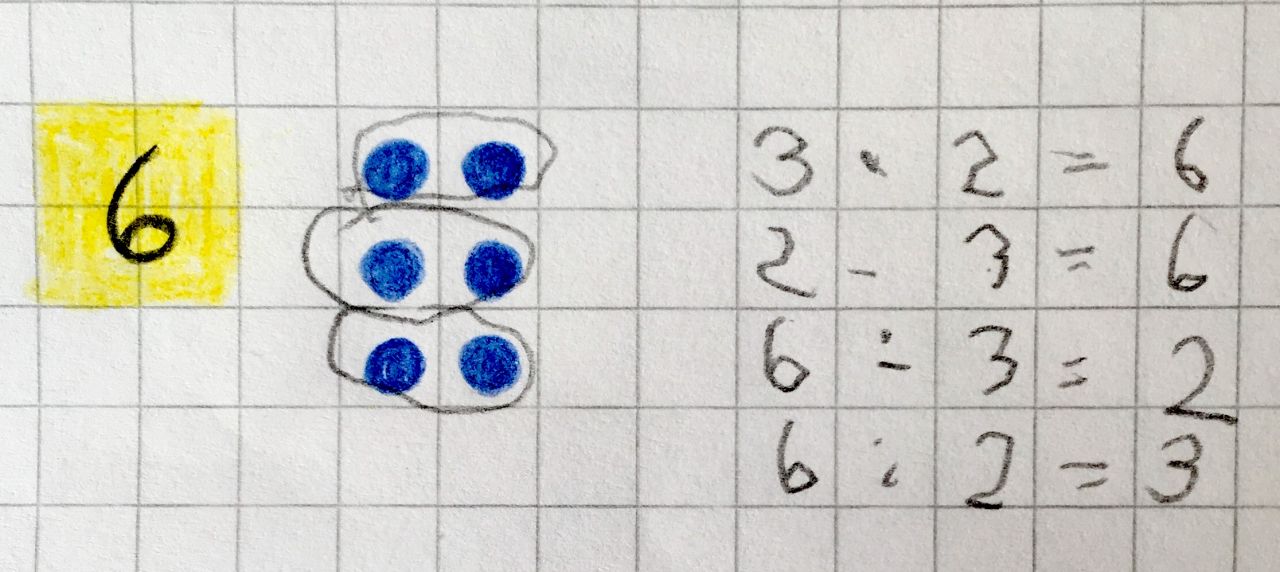
Alternativ können die Kinder auch angeregt werden, zu der gegebenen Zahl zunächst selber ein Punktefeld zu legen oder zu zeichnen, die entsprechenden Mal- und Geteiltaufgaben zu notieren und in das Punktefeld einzuzeichnen.
Reduktion
Vorgabe von drei Zahlen
Material: AB, Stift
Es werden drei Zahlen vorgegeben, zu denen vier Aufgaben notiert werden sollen.
Wichtig: Hier gilt es zu erkennen / zu klären, dass die größte Zahl immer die Gesamtmenge an Plättchen darstellt, d.h. sie ist das Ergebnis der Malaufgaben bzw. stellt die zu teilende Menge (Dividend) dar.
Beispiel "Drei Zahlen und vier Aufgaben":
Eine weitere Möglichkeit der Reduktion:
Je nach Lernvoraussetzungen der Kinder kann es sinnvoll sein, nur jeweils eine Mal- und eine Geteiltaufgabe notieren zu lassen.
Beispiel "Aufgabe und Umkehraufgabe":
Reduktion
"Immer zwei Aufgaben"
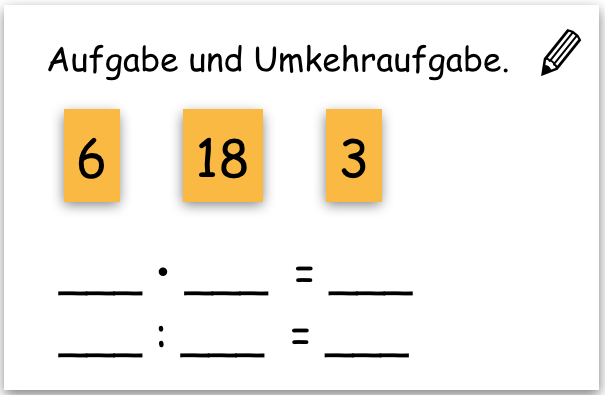
FOKUSSIERUNG AUF DAS FINDEN EINER AUFGABE UND DER ZUGEHÖRIGEN UMKEHRAUFGABE
Material: Wendeplättchen, Darstellungen von Punktefeldern, AB, Stift
Die Kinder werden angeregt, zu einem gegebenen Punktefeld eine Divisionsaufgabe und die zugehörige Multiplikationsaufgabe (Umkehraufgabe) zu finden und zu notieren. In Bezug auf das Punktefeld ist zunächst eine Konzentration auf die Grundsituation des Aufteilens sinnvoll (vgl. hierzu Hintergrund "Operationen verstehen").
Beispiel "Punktefeld":
Beispiel für eine mögliche Notation:
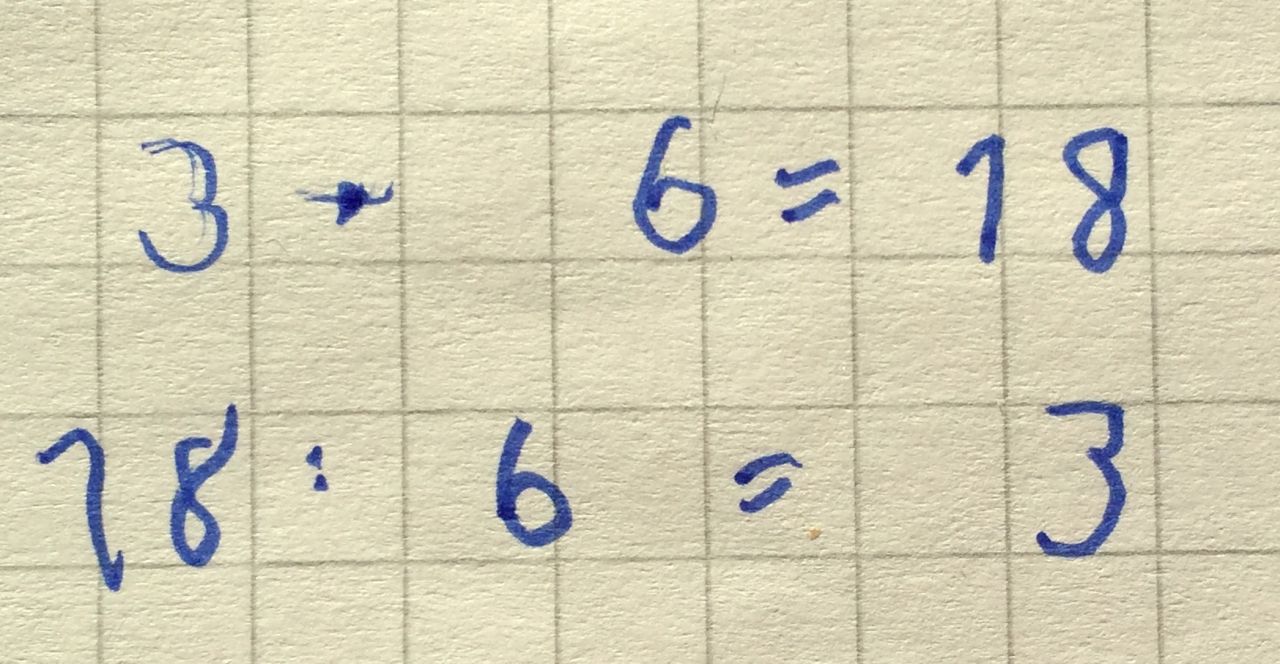
Variation: Neben dem Punktefeld wird die Multiplikationsaufgabe (alternativ die Divisionsaufgabe) vorgegeben und die zugehörige Umkehraufgabe muss notiert werden.
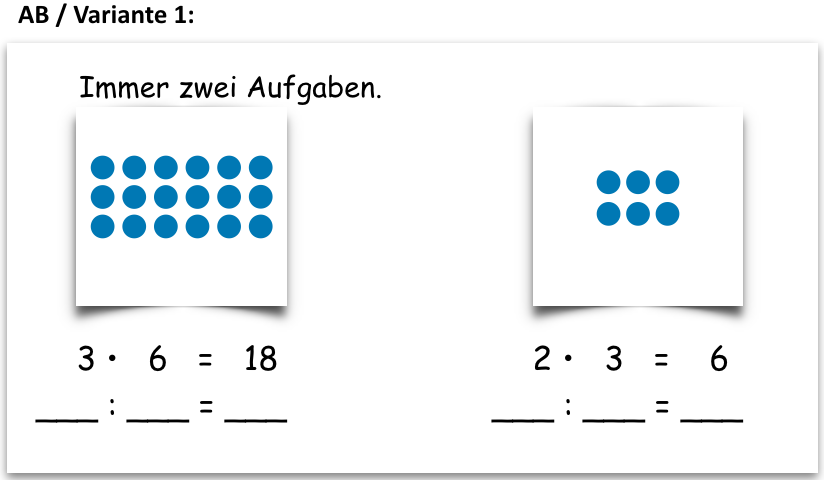
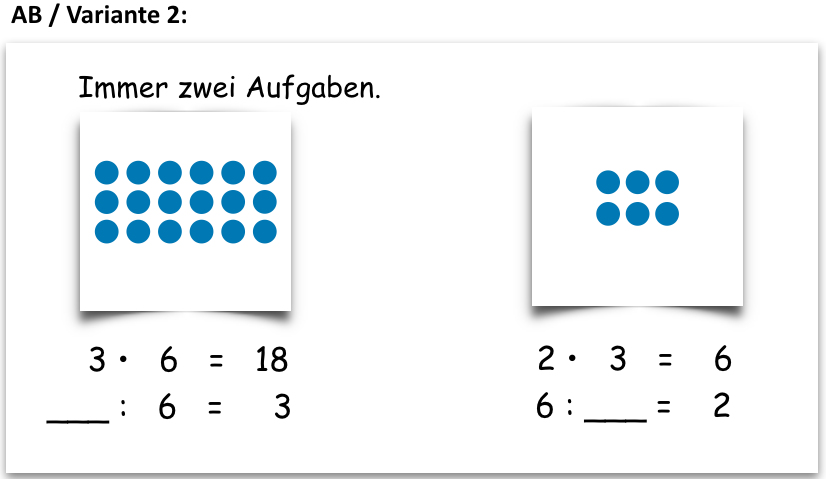
Eine zusätzliche Unterstützung kann das Einzeichnen der Divisionsaufgabe in das Punktefeld bieten.
Reduktion
Fokussierung auf Multiplikationsaufgaben
Material: Wendeplättchen, Darstellungen von Punktefeldern, AB, Stift
Je nach Lernvoraussetzungen des einzelnen Kindes kann es sinnvoll sein, den Fokus auf die Notation von Multiplikationsaufgaben zu legen und das Finden von Divisionsaufgaben noch zurückzustellen.
Hier gibt es zum einen die Möglichkeit, die Kinder auf der symbolischen Ebene arbeiten zu lassen:
Beispiel "Finde Malaufgaben zu der Zahl 6":
Zusätzlich können die Kinder angeregt werden, zu den Aufgaben passende Punktefelder zu zeichnen oder mit Plättchen zu legen. Hierdurch wird die Aufmerksamkeit der Kinder zum einen auf eine der notierten Multiplikationsaufgaben gerichtet. Zugleich stellt das Zeichnen eines Punktefeldes auch eine "Übersetzungsleistung" dar (vgl. hierzu Modul Hintergrund „Operationen verstehen“): symbolische Darstellung → Bild.
Ein mögliches Punktefeld kann auch durch die Lehrkraft vorgegeben werden. Allerdings wird hierdurch die Anzahl der möglichen Aufgaben eingeschränkt, da die Aufgaben durch das Punktefeld bereits festgelegt sind (6 als Ergebnis oder 6 als Faktor).
Reduktion
Sortieren von Aufgaben (Aufgabenfamilien bilden)
Material: Sortiertafel, vorgegebene Aufgaben
Die Kinder erhalten Karten mit verschiedenen Mal- und Geteiltaufgaben. Auf einer Sortiertafel werden die vier Aufgaben, die zu einer Aufgabenfamilie gehören, einander zugeordnet (vgl. hierzu auch die Basisaktivität "Sortieren und Zuordnen von Termen").
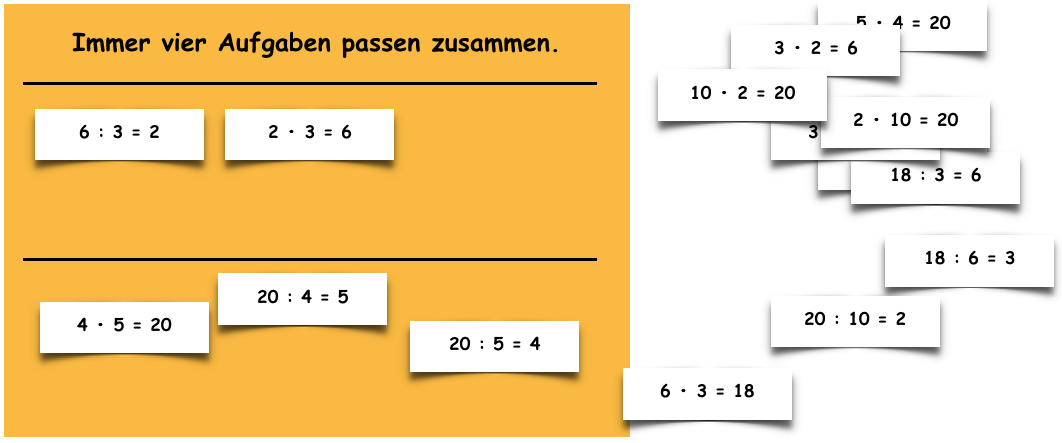
Variation (Aufgabe und Umkehraufgabe):
Analog zur obigen Aufgabe erhalten die Kinder Karten mit verschiedenen Mal- und Geteiltaufgaben. Die Aufgabe besteht nun allerdings darin, immer nur zwei Aufgaben (d.h. Aufgabe und zugehörige Umkehraufgabe) oder - alternativ - immer nur zwei Terme einander zuzuordnen.
Reduktion
Sortieren und Zuordnen ausgewählter Darstellungen
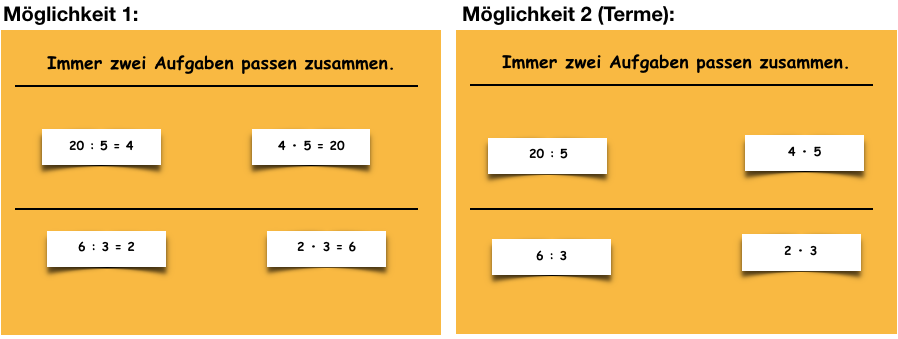
Material: Sortiertafel, Karten mit verschiedenen Darstellungen
Den Kindern wird eine reduzierte Anzahl an Darstellungen angeboten, die einander zugeordnet werden sollen. Hierbei kann der Fokus - je nach Lernvoraussetzungen der Kinder und mit Blick auf die individuellen Kompetenzerwartungen – auf die Übersetzung bestimmter Darstellungen gelegt werden (vgl. auch die Praxisbeispiele der Basisaktivität "Sortieren und Zuordnen verschiedener Darstellungen").
Erweiterung
Mehrere Aufgabenfamilien zu einer Zahl
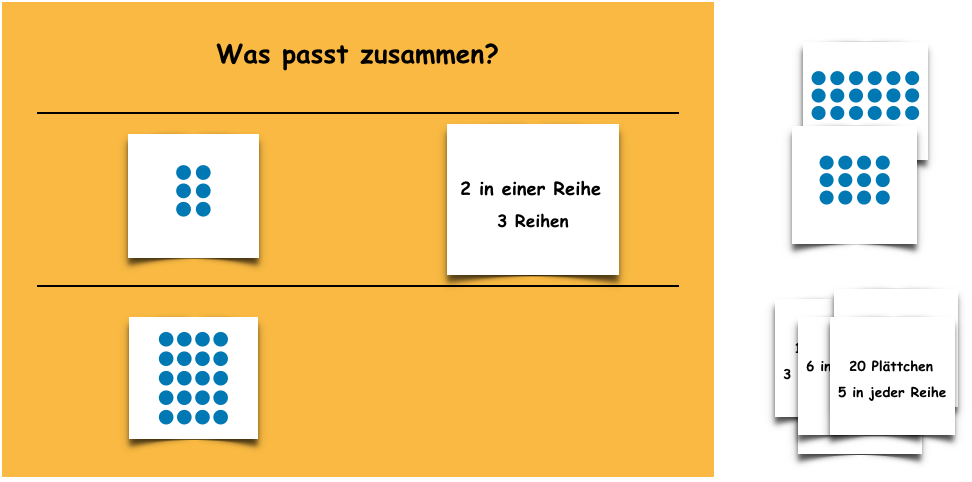
Material: AB, Stift
Zu einer vorgegebenen Zahl sollen mehrere verschiedene Aufgabenfamilien notiert werden. Da die jeweilige Position der Zahl in einer Aufgabe nicht vorgegeben ist, kann die Zahl in einer Multiplikationsaufgabe als Ergebniszahl oder Faktor auftreten und in einer Divisionsaufgabe als Dividend, Divisor oder Ergebnis.
Soll die Anzahl der möglichen Aufgabenfamilien eingegrenzt werden, kann als Bedingung vorgegeben werden, dass die vorgegebene Zahl die Ergebniszahl einer Multiplikationsaufgabe (bzw. Dividend einer Geteiltaufgabe) ist.
Beispiel:
"12 als Ergebnis einer Malaufgabe - Finde alle Aufgabenfamilien. Wie gehst du vor?"
Mögliche Aufgabenfamilien:
Erweiterung
Aufgabenfamilien zu einer selbst gewählten Zahl finden
Material: AB, Stift
Die Kinder haben die Möglichkeit, selber eine Zahl zu bestimmen, zu der sie dann jeweils zwei Mal- und zwei Geteiltaufgaben finden. Auch Zahlen aus dem erweiterten Zahlenraum können ausgewählt werden.
Beispiel für eine Aufgabenfamilie zu der selbst gewählten Zahl 444:
Erweiterung
Vier Zahlen - Wie viele Aufgaben?
Material: AB, Stift
Die Kinder erhalten vier Zahlen wie z.B. 2, 3, 6, 18.
Die Aufgabenstellung lautet: Schreibe alle Mal- und Geteiltaufgaben auf. Wie gehst du vor?
Mögliche Aufgaben: 2·3=6; 3·2=6; 6:2=3; 6:3=2; 3·6=18; 6·3=18; 18:3=6; 18:6=3
Erweiterung
Beschreiben und Begründen aus der Vorstellung heraus
Material: AB, Stift
Im Gegensatz zur Basisaktivität (vgl. Beschreiben und Begründen sowie Dokumentation der Aufgaben) wird bei der Erweiterung das Beschreiben und Begründen ohne ein sichtbares Punktefeld eingefordert. D. h., die Kinder beschreiben ein mögliches zu der Aufgabenstellung passendes Punktefeld aus der Vorstellung heraus.
Auch hier ist möglich, dass die Kinder selbständig formulieren oder vorgegebene Sätze ergänzen:
Möglichkeiten individueller Unterstützung
- Zur Fokussierung von Reihen in den Plättchendarstellungen eine "Lupe" verwenden:
- Statt Wendeplättchen Wendesteine zum Legen der Punktefelder nutzen.
-
Zur Verbalisierung Wortbausteine und Sprachmuster vorgeben (vgl. hierzu auch Basisaktivität „Beschreiben und Begründen“ sowie „Dokumentation der Aufgaben").
Möglichkeiten zur individuellen Unterstützung
Zur Synchronisierung von formaler und ikonischer Darstellung und Entlastung des kognitiven Arbeitsgedächtnisses die App Malrechnen nutzen
Mit der App Malrechnen (verfügbar auf iOS-Geräten, Stand Januar 2023; nähere Informationen zu der App finden Sie unter Lernsoftware Mathematik) können Lernende Beziehungen zwischen Tauschaufgaben in verschiedenen Darstellungsformen der Multiplikation synchron erkunden.
Einblicke in die App Malrechnen
Am Hunderterfeld können mittels Touch-Funktion beliebige Aufgaben erstellt und verändert werden. In der symbolischen Darstellungsform werden dazu synchron Multiplikationsaufgaben und (optional) Divisionsaufgaben angezeigt. Die Aufgaben lassen sich mit Abdeckstreifen verblenden und die Schüler:innen können dann die am Hunderterfeld dargestellte Malaufgabe und das Ergebnis eintippen. Dieses wird automatisch auf Korrektheit kontrolliert. Zur Entlastung des Arbeitsgedächtnisses können die Aufgaben ohne den Abdeckstreifen automatisiert berechnet werden, sodass sich die Kinder auf die Erkundung von Multiplikator, Multiplikand und Produkt (sowie optional Dividend, Divisor und Quotient) im Zusammenhang mit der Veränderung der Darstellung konzentrieren können. Ergänzend kann auch eine synchrone Beschriftung des Punktefelds erfolgen (Anzahl der Spalten und Anzahl der Plättchen in den Spalten bzw. Anzahl der Zeilen und Anzahl der Plättchen in den Zeilen). Eine Einblendung der passenden Additionsaufgabe ist ebenfalls möglich.
Zur sprachlichen Unterstützung können die Multiplikationsaufgaben (z. B. „sieben mal fünf“) sowie die Darstellung am Hunderterfeld (z. B. „sieben Spalten mit 5 Plättchen“) vorgelesen werden. Ergänzend ist es möglich, einen Zahlenstrahl einzublenden, der sich ebenfalls synchron zur Punktdarstellung oder der Multiplikations- bzw. Divisionsaufgabe verändert. Damit die Ansicht für Kinder mit Unterstützungsbedarf nicht zu überladen ist, bietet es sich an, je nach Zielstellung der Förderung, über die App-Einstellungen einzelne Funktionen zu fokussieren.
Mit Blick auf die Basisaufgabe „Immer vier Aufgaben“ bieten sich verschiedene Arbeitsaufträge mit der App Malrechen an, die ihren Einsatz als individuelle Unterstützungsmöglichkeit im inklusiven Mathematikunterricht finden können.
Analog zu der Reduktionsaufgabe „Aufgaben finden am Punktefeld“ können die Kinder diese Aufgabe mit der App Malrechnen lösen und mit dem digitalen Hunderterfeld Tauschaufgaben erkunden. Falls die anschließende schriftliche Notation schwerfällt, können die Kinder auch Screenshots erstellen und diese anschließend nebeneinander vergleichen.
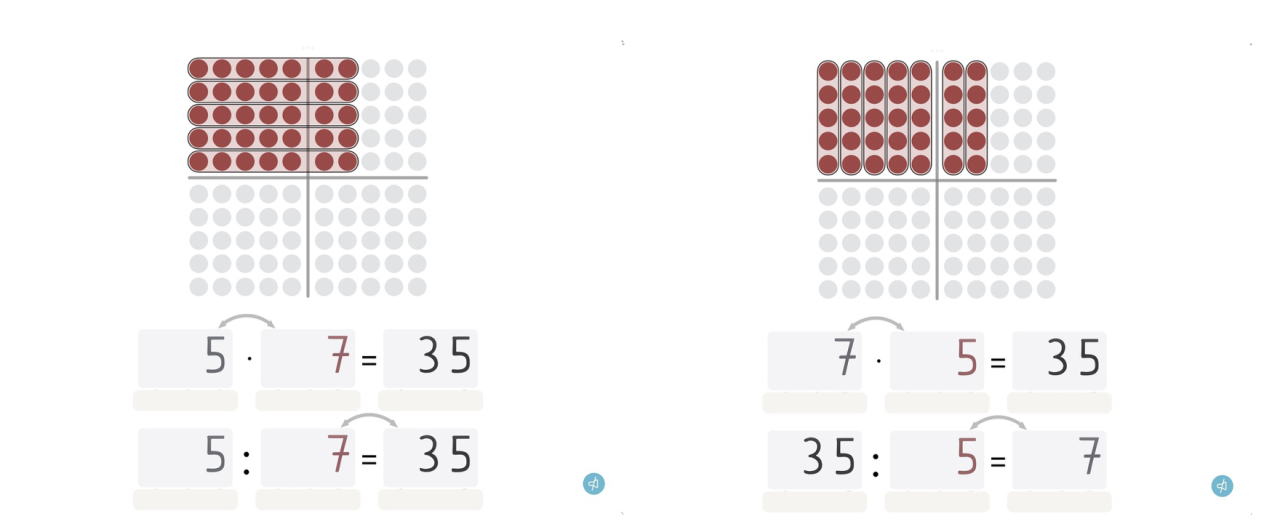
Ergänzend können die Kinder Leitfragen wie „Wie hängt die Multiplikationsaufgabe und die Divisionsaufgabe miteinander zusammen? Beobachte, wie sich die Zahlen verändern. Kannst du erklären, warum dies so ist?“ bearbeiten und so die synchronen Veränderungen der symbolischen und ikonischen Darstellungen untersuchen.
Für die Reduktionsaufgabe „Fokussierung auf Multiplikationsaufgaben“ kann die Lehrkraft in den Einstellungen der App die Ansicht der Divisionsaufgaben ausschalten, sodass die Schüler*innen zunächst die Multiplikationsaufgaben am digitalen Punktefeld erkunden können.
Neben der Sicherung der Entdeckungen der Kinder mittels Screenshots, können auch kurze Screencasts (also Bildschirmaufnahmen als Video-Aufzeichnungen) erstellt werden, die anschließend beschrieben und präsentiert werden können. In den folgenden Screencasts wurde die Sechserreihe (Video 1) und die Quadratzahlen (Video 2) systematisch mit Blick auf die Umkehraufgaben untersucht.
Erkundungen zu der Sechserreihe mit der App Malrechnen
Erkundungen zu Quadratzahlen mit der App Malrechnen
