Differenzsensible Unterrichtsplanung
Ebenso wie die Lerninhalte im inklusiven Mathematikunterricht sich nicht grundsätzlich von einem Mathematikunterricht unterscheiden, der nicht inklusiv ausgerichtet ist, entspricht auch die Unterrichtsvorbereitung in den Grundzügen der üblichen Praxis. Allerdings müssen bei der Planung nicht nur die individuellen mathematischen Lernstände der Schülerinnen und Schüler bedacht werden, sondern auch die verschiedenen sensorischen, kognitiven, emotionalen, sprachlichen oder körperlichen Lernvoraussetzungen (s. Abbildung 1).
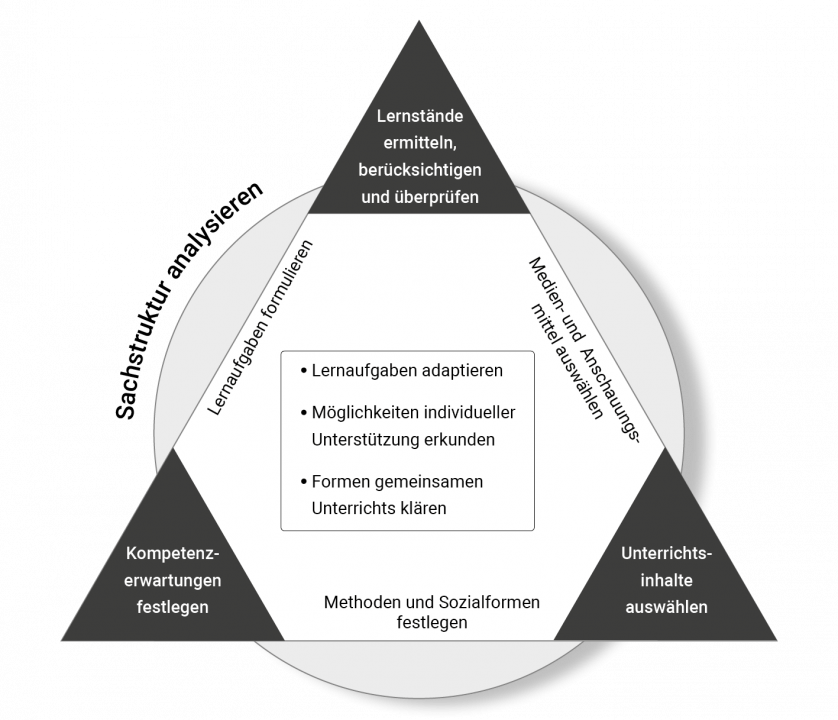 Abbildung 1: Übersicht differenzsensible Unterrichtsplanung
Abbildung 1: Übersicht differenzsensible Unterrichtsplanung
Um allen Kindern einen gleichberechtigten Zugang zu den Lernangeboten im Mathematikunterricht zu ermöglichen, gilt es, durch gezielte methodische oder mediale Unterstützungsmaßnahmen Barrierefreiheit zu gewährleisten (vgl. KMK, 2011).
Aus fachdidaktischer Sicht stellt sich vor allem die Frage, wie es gelingen kann, über die Arbeit an einem Lerngegenstand gemeinsame Zielsetzungen zu verfolgen und zugleich auch zieldifferentes Arbeiten zu ermöglichen – ohne den fachlichen Anspruch aufzugeben.
Hierfür gilt es, die fachlichen Möglichkeiten der Mathematik als Wissenschaft erforschbarer Muster und Strukturen auszunutzen und zugleich zu erkunden, auf welche Weise der fachliche Inhalt Raum für Vielfalt, Kreativität und individuelle Entwicklungs- und Lernverläufe lässt.
Raum für Vielfalt vom Fach aus wird geschaffen, indem die Begegnung mit dem mathematischen Lerninhalt auf unterschiedlichen Wegen möglich ist bzw. ermöglicht wird, z.B. durch verschiedene denkbare ...
-
... Lösungswege und Lösungen,
-
... Entdeckungen,
-
... Vorgehensweisen,
-
... Handlungen mit Materialien,
-
... Beschreibungen und Erläuterungen,
-
... Zeichnungen und Skizzen,
-
... Anschauungs- und Hilfsmittel,
-
... Darbietungen des Lehrgegenstandes,
-
...
Differenzsensible Unterrichtsplanung meint demnach, dass Unterrichtsinhalte unter Berücksichtigung individueller Lernstände und unterschiedlichster Lernvoraussetzungen so aufbereitet werden, dass vielfältige mögliche, fachliche Zugänge genutzt werden können.
Inklusiver Mathematikunterricht schöpft so die Möglichkeiten des Spiralprinzips aus: „Jedem Kind kann auf jeder Entwicklungsstufe jeder Lehrgegenstand in einer intellektuell ehrlichen Form erfolgreich gelehrt werden“ (Bruner, 1973, S. 44).
Im Folgenden soll erläutert werden, wie und an welchen Stellen der Unterrichtsplanung ein solch differenzsensibler Blick zu einem barrierefreien Mathematikunterricht mit Raum für Vielfalt führen kann.
Die formulierten Leitfragen und Beispiele sollen die theoretischen Ausführungen unterstützen und als konkrete Umsetzungsideen dienen.
Sachstruktur analysieren
-
Welche fachwissenschaftliche Struktur besitzt der Lerninhalt?
-
Wie gestaltet sich die Kompetenz-/ Lernentwicklung im Sinne des Spiralprinzips?
Die Analyse der Sachstruktur des Lerninhaltes korrespondiert mit den anderen Planungsschritten und bildet den Hintergrund, auf der die anderen Planungsschritte erst möglich sind.
Erst mit dem Wissen um die Sachstruktur kann ein passender Unterrichtsinhalt ausgewählt, können Kompetenzerwartungen formuliert und die themenbezogenen Lernstände bestimmt werden.
Gleichzeitig beeinflusst die Auswahl des Lerninhaltes aber auch, welcher Bereich des mathematikdidaktischen und fachwissenschaftlichen Hintergrundwissens in den Fokus rückt und genau analysiert werden muss.
"Ziel der Sachanalyse ist es (...), sich der Strukturen und Beziehungen des Unterrichtsgegenstandes bewusst zu werden und diese auf den didaktischen Planungsprozess beziehen zu können“ (Heckmann & Padberg, 2008, S. 71).
In einer Sachanalyse wird der mathematische Inhalt vorab in der Tiefe erkundet und der fachliche sowie didaktische Hintergrund erarbeitet. Bei der Planung von inklusivem Mathematikunterricht ist diese inhaltliche Erarbeitung in Hinblick auf die weitere Planung besonders relevant, da so der Facettenreichtum des mathematischen Gegenstands und unterschiedliche Lern- und Förderchancen leichter erkannt werden können. Bei der Analyse ist dabei der differenzsensible Blick auf den Lernprozess beim Kompetenzerwerb und die Auffächerung des Unterrichtsinhalts im Sinne des Spiralprinzips besonders wertvoll.
Eine Sachanalyse öffnet so den Blick auf mögliche Förder- und Differenzierungsmaßnahmen und hilft bereits bei der Auswahl geeigneter Lernaufgaben, Medien und Anschauungsmittel sowie Methoden und Sozialformen. Sie bildet die Grundlage, um eine Differenzierung vom Fach aus vornehmen zu können.
Lernstände ermitteln, berücksichtigen und überprüfen
-
Wie kann überprüft werden, an welcher Stelle sich die Schülerinnen und Schüler im Lernprozess befinden oder ob die angestrebten Kompetenzen tatsächlich erworben wurden?
„Eine inklusive Unterrichtsgestaltung beruht auf einer den Lernprozess begleitenden pädagogischen Diagnostik und einer kontinuierlichen Dokumentation der Lernentwicklung“ (KMK, 2011, S.10).
Um die Schülerinnen und Schüler optimal in ihrem Lernprozess begleiten und unterstützen zu können, ist es deshalb notwendig, vor der Durchführung einer Unterrichtseinheit zu überprüfen, an welcher Stelle des Lernprozesses die Kinder sich gerade befinden.
Während und nach der Durchführung gilt es dann zu beobachten und festzustellen, ob die angestrebten Kompetenzen tatsächlich erworben werden konnten.
Kompetenzerwartungen festlegen
-
Welche inhalts- und prozessbezogenen Kompetenzen soll die Lerngruppe erwerben?
Im Sinne einer kompetenzorientierten Unterrichtsplanung sollte jedes Unterrichtsvorhaben den Schülerinnen und Schülern ermöglichen, die im Lehrplan vorgegebenen Kompetenzerwartungen zu erwerben.
Ausgangspunkt und Grundlage der Unterrichtsplanung ist somit der Lehrplan mit den Kompetenzerwartungen aus einem Bereich des Faches. Die Auswahl orientiert sich an den aktuellen Lernausgangslagen bzw. Kompetenzständen der Schülerinnen und Schüler (vgl. hierzu auch den Planungsschritt: Lernstände ermitteln, berücksichtigen und überprüfen).
... dabei individuelle Lernziele berücksichtigen
-
Welche fachlichen Inhalte sind für das Kind gegenwärtig von zentraler Bedeutung?
-
Wo besteht die Zone der nächsten Entwicklung?
In inklusiven Settings müssen einerseits die Standards und Zielsetzungen für allgemeine schulische Abschlüsse und andererseits die individuellen Kompetenzen der Lernenden berücksichtigt werden (vgl. KMK, 2011).
Das ist notwendig, da ungefähr die Hälfte aller Schülerinnen und Schüler mit sonderpädagogischem Unterstützungsbedarf zieldifferent unterrichtet werden. Es werden in diesem Fall für jedes Kind individuell fachliche Entwicklungsziele festgelegt (vgl. Förderschwerpunkte: AO-SF).
Diese werden in Zusammenarbeit mit der sonderpädagogischen Lehrkraft erarbeitet und in Lern- und Entwicklungsplänen verschriftlicht. Dabei werden "z. B. individuell weniger relevante Inhalte gestrichen oder verkürzt, besonders wichtige Inhalte vertieft, zu anspruchsvolle Inhalte vereinfacht behandelt“ (Wember, 2013, S. 386).
Die individuelle Förderung einzelner Kinder erfolgt idealerweise an einem ausgewählten, fachlichen Inhalt, um somit fachliche und entwicklungsbezogene Aspekte miteinander zu verzahnen.
Unterrichtsinhalte auswählen
-
Welcher Lerninhalt eignet sich dazu, die angestrebten Kompetenzen zu erwerben?
-
Welche fachlichen Inhalte sind grundlegend für den Aufbau und die (Weiter-) Entwicklung dieses mathematischen Wissens und Könnens?
Nach der Festlegung der allgemeinen und individuellen Kompetenzerwartungen steht man demnach vor der Herausforderung, den Unterrichtsinhalt so passend auszuwählen, dass trotz (möglicherweise) unterschiedlicher Ziele gemeinsames Lernen entstehen kann.
Es muss also ein Unterrichtsinhalt ausgewählt werden, der sich dazu eignet, einen Bogen zwischen den Vorerfahrungen und unterschiedlichen Lernvoraussetzungen der Schüler „und den intendierten fachinhaltlichen und prozessbezogenen Kompetenzen zu schlagen“ (Barzel & Holzäpfel, 2010, S. 4).
"Das gemeinsame Ziel bezieht sich letztlich auf den gemeinsamen Gegenstand, weist aber zieldifferente Ausprägungen auf. In diesem Sinne arbeiten die Lernenden an einer gemeinsamen Sache, ohne dass dabei jeder dasselbe zu leisten hat“ (Häsel-Weide & Nührenbörger, 2015, S. 61 in Anlehnung an Feuser 1995).
Die Lehrkraft kann hier auf verschiedene fachliche Themen zugreifen, da die durch den Lehrplan vorgegebenen Inhalte einige Spielräume und Entscheidungsfelder offenlassen.
Besonders geeignet für den Unterricht in heterogenen Lerngruppen erweisen sich Unterrichtsinhalte, die den fundamentalen Ideen für den Mathematikunterricht entsprechen und bei denen der Kompetenzaufbau im Sinne des Spiralprinzips durch eine wiederkehrende Beschäftigung mit mathematischen Zusammenhängen auf immer höherem Niveau mit steigendem Abstraktionsgrad erfolgt.
So kann ein zentraler Lerninhalt für alle ausgewählt werden, um anschließend eine adaptive Lernumgebung und dafür notwendige Lehrstrategien zu entwickeln.
Differenzsensible Leitfrage zur Auswahl eines Unterrichtsinhaltes:
-
Gibt es einen Unterrichtsinhalt, der für alle Kinder eine auf ihre Lernziele ausgerichtete „fachliche Gemeinsamkeit“ beinhaltet?
Lernaufgaben bestimmen
-
Welche Aufgaben sind geeignet den Ansprüchen an inklusives Lernen nach Gemeinsamkeit und Individualisierung nachzukommen?
Aufgabenstellungen sollten so weitreichend und umfassend sein, dass jedes Kind auf seinem Niveau „einsteigen“ und seinen Teil zum gemeinsamen Vorhaben beitragen kann (vgl. Rehle, 2009, S. 184).
Ergiebige Aufgaben im Sinne der Bildungsstandards Mathematik eignen sich in besonderem Maße für stark heterogene Lerngruppen.
Sie bieten reichhaltige Möglichkeiten für mathematische Aktivitäten, können zum Erkunden, Darstellen und Erörtern mathematischer Zusammenhänge genutzt werden, bieten Raum für die sozial-interaktive Auseinandersetzung der Kinder untereinander und können an individuelle Gegebenheiten angepasst werden, sodass individuelle Entwicklungs- und Lernverläufe realisiert werden können (vgl. Häsel-Weide & Nührenbörger, 2015, S. 64).
Gemein ist all diesen Aufgaben das Merkmal der „Offenheit“. Wahlmöglichkeiten z.B. bezüglich der Arbeitsmittel sowie der Darstellung erweitern das Differenzierungspotential des Formats.
Meist können auch traditionelle Schulbuchaufgaben durch Adaptionen oder Variationen so verändert werden, dass sie die notwendigen Bedingungen für ein inklusives Setting erfüllen (vgl. Sie hierzu auch den folgenden Planungsschritt "Lernaufgaben adaptieren").
Differenzsensible Leitfragen zur Auswahl einer Lernaufgabe:
-
Bietet die Aufgabe Raum für Vielfalt, d.h. die Möglichkeit verschiedener Zugänge, Lösungswege und Lösungen, Hilfsmittel, Vorgehensweisen, Darstellungen und Dokumentationen?
-
Gibt es Möglichkeiten der Reduktion und Erweiterung ohne Aufgabe des fachlichen Anspruchs?
Lernaufgaben adaptieren
-
Welches natürliche Differenzierungspotential bietet die Aufgabe und wie können den Lernenden in ihrer Verschiedenheit weitere Zugänge geboten werden, sodass sie eigenständig Ideen entwickeln und sich mit anderen austauschen können?
Im differenzsensiblen Unterricht werden grundlegende Aufgabenstellungen (Basisaufgaben) für alle Kinder so aufgefächert, dass auch reduzierte oder erweiterte Anforderungen gesetzt werden können, die einerseits inhaltlich an das gemeinsame Thema gebunden sind, andererseits themenfokussiert unterschiedliche Lern- und Entwicklungsverläufe ermöglichen.
Bei der Adaption der Aufgabe werden der Facettenreichtum und die inhaltliche Bandbreite der mathematischen Aufgabenstellung erkundet. Es entsteht so ein Aufgabenfeld, das sich um eine Basisaufgabe rankt: mit möglichen Basisaktivitäten sowie Möglichkeiten zur Reduzierung oder Erweiterung der Anforderungen.
Erst jetzt wird die inhaltliche Bandbreite der Aufgabenstellung und das ganze Differenzierungspotential deutlich. Es wird sichtbar, wie die individuellen Lernziele mit Hilfe von geeigneten Aufgabenstellungen erreicht werden können und wo Schnittstellen zwischen den allgemeinen und individuellen Lernzielen bestehen.
Auf diese Weise entstehen "große Aufgaben“ wie sie in den Bildungsstandards angedacht sind: Aufgaben, "die der Leistungsheterogenität von Grundschülern dadurch Rechnung tragen, dass sie im gleichen inhaltlichen Kontext ein breites Spektrum an unterschiedlichen Anforderungen und Schwierigkeiten abdecken. Dadurch können die Aufgabenbeispiele zugleich als Muster für einen differenzierenden Unterricht fungieren, in dem alle Kinder am gleichen Inhalt arbeiten, aber nicht unbedingt dieselben Aufgaben lösen" (KMK, 2004, S. 16).
Medien und Anschauungsmittel auswählen
-
Welche Medien und Anschauungsmittel können in Zusammenhang mit dem jeweiligen Lerngegenstand eingesetzt werden? Welche Unterschiede in Bezug auf die verschiedenen Anschauungsmittel gibt es?
Bei der Auswahl der Anschauungsmittel ist darauf zu achten, dass immer eine Verbindung zwischen der symbolischen Notationsweise und der Darstellung hergestellt werden kann und verschiedene Darstellungsmöglichkeiten verknüpft werden können. Es gilt, Abstraktionsprozesse anzuregen. Um solche Verknüpfungen zu unterstützen und herzustellen, „kommt der sprachlichen Begleitung und der gemeinsamen Reflexion eine wichtige Bedeutung zu“ (Krähenmann et al., 2015, S. 50).
Differenzsensible Leitfragen zur Auswahl geeigneter Anschauungsmittel:
-
Erlaubt das Material den Kindern die Entwicklung unterschiedlicher, individueller Lösungswege?
-
Kann das Material als Lösungshilfe, Lernhilfe und/ oder Argumentations- und Kommunikationshilfe dienen?
Methoden und Sozialformen festlegen
-
Wie können trotz Differenzierung und unterschiedlichen Aneignungsniveaus gemeinsame Lernmöglichkeiten geschaffen und die aktive Auseinandersetzung mit dem Lerngegenstand angeregt werden?
Insbesondere der Austausch über verschiedene Verständnisstufen bei der gemeinsamen Arbeit kann mathematische Lernprozesse auslösen: "Die leistungsschwächeren Schülerinnen und Schüler können sich an den anderen Kindern orientieren, während die leistungsstärkeren durch den reflexiven Blick auf die ‚niedrigere’ Stufe neue Einsichten erhalten“ (Häsel-Weide & Nührenbörger, 2015; Scherer, 2015).
Jede individualisierende Lernaufgabe ist deshalb grundsätzlich auf Austausch, Ergänzung und Gemeinsamkeit zu beziehen (vgl. Rehle, 2009). "Gemeinsamkeit stellt sich in einer heterogenen Lerngruppe nicht von selber her, sondern muss auch in integrativen bzw. inklusiven Settings immer wieder neu erarbeitet werden“ (Lütje-Klose & Miller, 2015, S. 19).
Sowohl gemeinsame Erarbeitungs- und Reflexionsphasen, die das Lernen am Gemeinsamen Gegenstand stärken, als auch Arbeitssequenzen in Einzelarbeit oder individuelles, produktives Üben bilden so gleichberechtigte Bausteine für einen differenzsensiblen Unterricht (vgl. Moser Opitz, 2009).
In Partner- bzw. Gruppenaktivitäten oder gemeinsamen Klassensequenzen (insbesondere in Einstiegs- und Reflexionssequenzen) sollen die Kinder sich immer wieder über den Lerngegenstand und ihre individuellen Lernergebnisse austauschen. Auch die Präsentation von (Teil-) Ergebnissen und Mathekonferenzen sollte angeregt werden.
Bei der differenzsensiblen Unterrichtsplanung geht es demnach darum, die Methoden und Sozialformen so auszuwählen, dass gemeinsame Lerngelegenheiten geschaffen werden und eine aktive Auseinandersetzung mit dem Lerngegenstand angeregt wird.
Differenzsensible Leitfragen zur Auswahl von Methoden und Sozialform:
-
Wie kann einerseits die Arbeit an individuellen Lernzielen und andererseits die Interaktion und Reflexion über den Lerngegenstand im Klassenverband gefördert werden?
-
Inwiefern können die geplanten Differenzierungsmaßnahmen methodisch gestützt werden?
Möglichkeiten individueller Unterstützung erkunden
-
Welche weiteren individuellen Unterstützungsmaßnahmen sind notwendig, um jedem Kind einen barrierefreien Zugang zum Lernangebot und der Lernumgebung zu ermöglichen?
Ergänzend zu den Überlegungen zu inhaltlichen Differenzierungsmaßnahmen müssen im inklusiven Mathematikunterricht weitreichendere Überlegungen zu eventuell zusätzlich notwendigen individuellen Unterstützungsmaßnahmen angestellt werden. Einerseits ist es wichtig, dass die Schülerinnen und Schüler die Aufgaben möglichst selbstständig bearbeiten und eigene Zugänge und Vorgehensweisen wählen können.
"Wenn dies jedoch nicht oder nur fehlerhaft gelingt, ist eine geeignete Unterstützung notwendig“ (Krähenmann et al., 2015, S. 54).
Einzelne Kinder benötigen gezielte Unterstützung "bei der Arbeitsorganisation, beim Lesen der Aufgabenstellung oder beim Darstellen von Ideen [...], sodass sie überhaupt in die Lage versetzt werden, die mathematische Entdeckung zu machen oder festzuhalten“ (Häsel-Weide & Nührenbörger, 2015, S. 60).
Die Lehrerin oder der Lehrer kann in diesen Momenten steuernd eingreifen oder weitere individuelle Unterstützungsmaßnahmen bereitstellen. "Die ‚Kunst‘ liegt darin, solche konkreten Hinweise und Anregungen zu geben, die es den Lernenden ermöglichen, den nächsten Lernschritt selber zu tun“ (Krähenmann et al., 2015, S. 54).
Bei Sinnesschädigungen sind z.B. darüber hinaus alternative sensorische Zugänge zu wählen, bei mangelhaften Leseleistungen werden "Hilfen bei der Textbearbeitung gewährt oder bildliche Medien angeboten, bei schwierigen Sozialverhalten Alternativen zur Kleingruppen eröffnet (...), Inhalte und Arbeitsweisen des Klassenunterrichts werden in Kleingruppenarbeit vor- oder nachbereitet oder in ausgewählten Lernbereichen durch begleitenden intensiven Unterricht gesichert“ (Wember, 2013, S. 386).
Das heißt zusätzlich zu der inhaltlichen Differenzierung müssen weitere Anpassungen in Form von optischen, akustischen oder anderen sensorische Gestaltungsprinzipien, dem Einsatz technischer Hilfsmittel oder der Modifikation sprachlicher Inhalte (z.B. die Zugänglichkeit der Unterrichtsinhalte in leichter Sprache) vorgenommen werden.
Diese individuellen Unterstützungsmaßnahmen sollten in Zusammenarbeit mit der sonderpädagogischen Lehrkraft individuell auf das Kind abgestimmt werden, um letztlich gemeinsames und individuelles Lernen zu ermöglichen (vgl. Häsel-Weide & Nührenbörger, 2015, S. 68).
Differenzsensible Leitfragen zur Planung individueller Unterstützungsmaßnahmen
-
Welches Kind hat bestimmte sensorische Beeinträchtigungen, die eine Adaption oder Variation der Medien oder bestimmte methodische Unterstützungsmaßnahmen notwendig machen?
-
Welche Lernenden benötigen besondere sprachliche Unterstützungsmaßnahmen entweder beim Sprachverstehen oder bei der Sprachproduktion?
-
Gibt es weitere besondere individuelle Lernvoraussetzungen, die bei der Unterrichtsplanung zu berücksichtigen sind?
Formen gemeinsamen Unterrichtens klären
-
Welche konkreten Aufgaben sollen die verschiedenen Beteiligten in dem geplanten Unterrichtsgeschehen übernehmen?
Viele Lehrkräfte unterrichteten lange Zeit relativ autonom in ihrem Klassenzimmer und innerhalb ihrer Schule. Im inklusiven Mathematikunterricht gilt es nun, sich mit vielfältigen anderen Personen und Institutionen auszutauschen und die Unterrichtsplanung entsprechend abzustimmen – z.B. mit Sonderpädagogen, Sozialpädagogen, Integrationskräften und außerschulischen Spezialisten wie Logopäden, Psychologen oder Ergotherapeuten.
Für das gemeinsame Handeln von zwei (oder mehreren) Lehrkräften im Unterricht können insbesondere sechs Formate unterschieden werden (vgl. Friend & Bursuck 2009, Serke et al. 2014).
Bei allen Formen des gemeinsamen Unterrichts ist es wichtig, die Aufgabenfelder und auch -verteilungen klar miteinander abzusprechen und den steten Austausch zwischen allen Mitgliedern des multiprofessionellen Teams über den gemeinsam verantworteten bzw. zu gestaltenden Mathematikunterricht zu pflegen.