Für den mathematischen Anfangsunterricht und insbesondere auch für Kinder mit Lernschwierigkeiten bedeutet dies, dass eine Beschäftigung mit und das Erkunden von Strukturen und Zusammenhängen zwischen Zahlen (und Operationen) von Beginn an zwingend notwendig ist (vgl. Gaidoschik, 2007).
Von direkten zu beziehungshaltigen Zahlvorstellungen
Bei Kindern im Vorschulalter bzw. bei Schulanfängern dominieren zunächst noch direkte Vorstellungen zu den einzelnen Zahlen, d.h. dass eine Zahl mit einem oder – je nach Kontext – mit mehreren konkreten Bildern bzw. Repräsentanten verbunden wird. Diese Kompetenz ist sehr wichtig für den Aufbau von Stützpunktvorstellungen im kardinalen Bereich, die letztlich auch zum Schätzen genutzt werden können.
Mit Blick auf das Nutzen von Basisaufgaben gehören hier auch direktive Vorstellungen zum Verdoppeln zu wie auch Vorstellungen über Zerlegungen der 10, die einen ersten Eckpfeiler dekadischer Vorstellungen darstellen.
Problematisch wird es allerdings, wenn die Kinder zu einer Zahl nur ein Bild isoliert verknüpfen können. Eine direkte, isoliert ausgeprägte Zahlvorstellung kann auch dann vorhanden sein, wenn Kinder bereits früh sehr kompetent die Zahlwortreihe aufzählen können.
Es ist möglich, dass dann ausschließlich der ordinale Zahlaspekt im Vordergrund steht und Zahlen nur in der Reihenfolge der Zahlwortreihe notiert oder genannt werden können.
Obwohl die Zahlen in einer Folge neben anderen Zahlen stehen und das Kind in der Lage ist, die Zahlen in ihrer richtigen Reihenfolge zu nennen oder aufzuschreiben, bedeutet dies nicht zwangsläufig, dass bereits Zahlbeziehungen und Zusammenhänge der Zahlen untereinander gesehen werden.
Weitere Informationen zur Bedeutung des ordinalen Zahlaspektes für die Entwicklung tragfähiger Zahlvorstellungen finden Sie in Hintergrund: Zahlaspekte beachten.
Beispiele für mögliche direkte Vorstellungen zu der Zahl 6:
Abbildung 1
Die Zahl 6 als konkrete, geschriebene Zahl an einem festen Platz in der Zahlwortreihe (Beispiele in Anlehnung an Ruwisch, 2015).
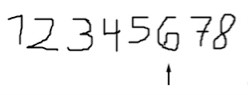Abbildung 2
Insbesondere kleinere Anzahlen bis 20 – aber auch bestimmte größere Anzahlen wie beispielsweise 100 oder 1000 – können wir in der Regel mit direkten Zahlvorstellungen verbinden.
Beispiel: Ein Buch mit ungefähr 1000 Seiten.
Abbildung 3
Beispiel: Der Tausenderwürfel
Abbildung 4
Im Allgemeinen stellen wir uns große Zahlen (also Zahlen über 100) eher "indirekt" vor; d. h. wir setzen sie aus vorstellbaren Zahlen und Größen zusammen. Anders gesagt, wir portionieren sie uns quasi.
Ein Beispiel: Wie viel sind eigentlich 1000 Kinder? Denken wir an 25 Kinder in einer Klasse und 100 Kinder in einem Jahrgang. Dann sind es ca. 400 Kinder an einer Grundschule. 1000 Kinder wären also ungefähr die Kinder von zwei bis drei Grundschulen.
Der Aufbau von Zahlvorstellungen zu größeren Zahlen gründet somit auf dem Erkennen und Nutzen von Zahlbeziehungen und Rechenstrategien (vgl. Ruwisch, 2015).
Zahlbeziehungen in kleinen Zahlenräumen
Jede Zahl ist in ein vielschichtiges und komplexes Beziehungsgeflecht eingebettet.
So ist die Zahl 6 beispielsweise das Doppelte der Zahl 3, das Dreifache der Zahl 2 und die Hälfte von 12 sowie ein Zehntel von 60 (hingegen ist 10 ein Sechstel von 60). Sie liegt zwischen den Zahlen 5 und 7, ist um eins mehr als 5 und eins weniger als 7, sie liegt zwischen 0 und 10, aber näher an der 10 als an der 0, sie lässt sich zerlegen in 1 und 5 oder 2 und 4 oder 3 und 3 usw..
Bereits in kleinen Zahlenräumen können und sollten diese vielfältigen kardinalen und ordinalen Beziehungen und Zusammenhänge zwischen Zahlen in den Mittelpunkt des Unterrichts gestellt und vertieft werden. Es ist ein Trugschluss zu glauben, dass für das Denken in Beziehungen bestimmte mathematische Kenntnisse und Fähigkeiten vorauszusetzen wären und dies eher etwas für leistungsstärkere Kinder sei.
Vielmehr gilt: „Zahlen in Beziehung zu einander zu denken lernt man, indem man Zahlen zu einander in Beziehung setzt“ (Gaidoschik, 2010a, S. 116).
Kardinale und ordinale Beziehungen zwischen Zahlen
Geht es im Anfangsunterricht um kardinale Beziehungen zwischen Zahlen, dann spielt zum einen der direkte Mengenvergleich (mehr, weniger oder gleich viele Elemente) und das Bestimmen der jeweiligen Differenzmenge (wie viel Elemente mehr?) eine zentrale Rolle.
Ein weiterer wichtiger Aspekt des Denkens in kardinalen Beziehungen umfasst das Zerlegen von Mengen in Teilmengen – anders gesagt, das Teil-Ganzes-Konzept.
Stehen ordinale Beziehungen zwischen Zahlen im Mittelpunkt, dann geht es um die Position der Zahlen in der Zahlwortreihe, d.h. es geht um das Bestimmen der Nachbarzahlen (Vorgänger und Nachfolger), das Vergleichen von Zahlen (größer, kleiner, gleich) sowie das Ordnen nach Größe und – bezogen auf die Zahlwortreihe – um die Abstände von Zahlen.
Diese verschiedenen Aspekte kardinaler und ordinaler Beziehungen zwischen Zahlen werden im Folgenden ausführlich dargestellt und näher erläutert (vgl. Schuler, 2013).
Gesetzt werden drei thematische Schwerpunkte:
-
Teil-Ganzes-Konzept
-
(An-)zahlen vergleichen
-
Zahlen positionieren
1. Teil-Ganzes-Konzept
Unter dem Begriff "Teil-Ganzes-Konzept“ wird die wichtige Erkenntnis verstanden, dass Zahlen zerlegbar und aus anderen Zahlen zusammengesetzt sind.
Zahlen repräsentieren nicht einfach eine bestimmte Menge, sondern diese ist wiederum aus Teilmengen zusammengesetzt.
„Das Verständnis, dass eine Menge in verschiedene Anzahlen zerlegt und wieder zusammengesetzt werden kann, stellt die Grundlage dar zur Erkenntnis, dass Zahlen auch Beziehungen zwischen Mengen modellieren“ (Scherer & Moser Opitz, 2010, S. 99).
Bereits im Alter von etwa 4 Jahren entwickeln Kinder in der Regel eine erste Vorstellung von Beziehungen zwischen Mengen. Resnick (1983) spricht hier von einem protoquantitativen Verständnis. "Beim protoquantitativen Verständnis handelt es sich um nicht-quantifizierte Zusammenhänge zwischen Zahlen (Mengen), wie z. B. die Einsicht, dass ein Ganzes, welches in zwei Teile geteilt wurde, nicht mehr oder weniger geworden ist [...]“ (Häsel-Weide, 2016, S. 8). Zudem können die Teile in Relation zueinander variieren ohne dass sich die Gesamtmenge verändert.
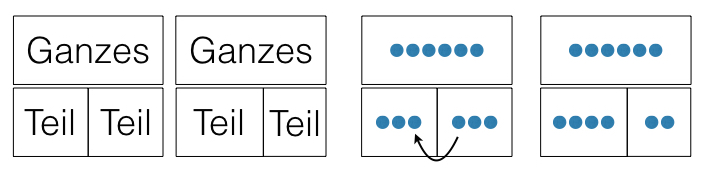Abbildung 5
Verfügen die Kinder dann zusätzlich über Zählkompetenzen, „erwächst ein Verständnis für die exakten numerischen Beziehungen zwischen den Teilen und dem Ganzen“ (Dornheim, 2008, S. 60).
Ein quantitatives Verständnis des Teile-Ganzes-Konzepts entwickelt sich im Kindergartenalter zunächst im kleinen Zahlenraum. Insbesondere kontextgebundene Aufgabenstellungen unterstützen die Einsicht in die numerische Erfassbarkeit der Beziehung zwischen einer Zahl und ihren Teilen sowie die Erkenntnis, dass sich Anzahlen in unterschiedliche Teilmengen zerlegen lassen.
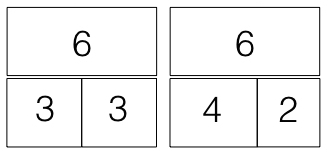Abbildung 6
Zahlen zerlegen (Aufbau und Entwicklung des Teil-Ganzes-Konzeptes):
Einsichten in die Beziehung zwischen einzelnen Teilen und dem Ganzen der Teile werden insbesondere durch die Ausbildung der Fähigkeit entwickelt, Zahlen zu zerlegen und die Beziehungen zwischen Zahlen und ihren Teilen numerisch zu erfassen.
In Bezug auf den Aufbau und die Entwicklung des Teil-Ganzes-Konzeptes geht es zunächst um das grundlegende Verständnis der Beziehungen, die sich in Zahlentripeln wie beispielsweise 7 – 5 – 2 oder 8 – 5 – 3 ausdrücken.
Allerdings ist es wichtig, dass sich dieses Verständnis langfristig auch auf weitere Zerlegungen ausweitet wie beispielsweise 7 – 3 – 3 – 1.
Beispielhafte Übungen: Eine elementare Möglichkeit, Teil-Ganzes-Beziehungen im Unterricht zu thematisieren, stellen beispielsweise Zerlegungsübungen mit Wendeplättchen oder Kugelketten dar.
Wichtig ist hierbei, dass die Kinder die Zerlegungen strukturiert erkennen können, da sie ansonsten zum Zählen der Teile angeregt werden. Sogenannte „Schüttelboxen“ bieten daher nur eingeschränkte Möglichkeiten der Förderung von Vorstellungen in Teil-Ganzes-Beziehungen.
Zahlzerlegungen finden ...
mit Kugelketten: Bei der Kugelkette können durch das Verschieben der Kugeln verschiedene Zahlzerlegungen gefunden werden, die dann anschließend dokumentiert werden. Durch den Einsatz eines Stiftes wird die Zerlegung hervorgehoben
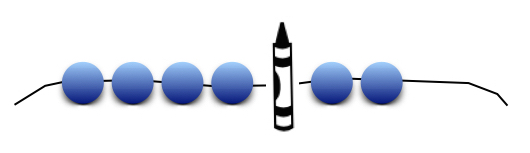Abbildung 7
Zahlzerlegungen finden ...
mit Wendeplättchen: Analog kann auch mit Wendeplättchen gearbeitet werden, wenn diese als einfarbige Plättchen eingesetzt werden.
Abbildung 8
Wichtig ist die anschließende Dokumentation der gefundenen Zerlegungen:
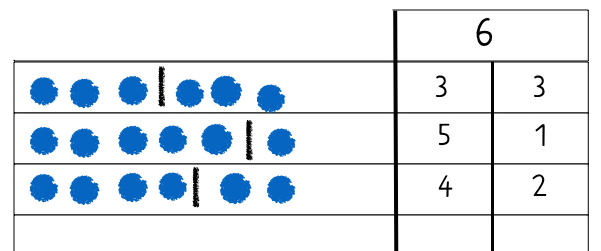Abbildung 9
Die Arbeit mit einer Menge von einfarbigen Elementen bietet den Vorteil, dass der Blick auf die Zerlegung der Menge gerichtet wird.
Wird die Zweifarbigkeit der Wendeplättchen für die Darstellung der Zerlegungen genutzt, kann das bei einigen Kindern dazu führen, dass nicht die Zerlegung einer Menge, sondern die Zusammensetzung von zwei Mengen im Fokus steht.
Haben die Kinder verschiedene Zerlegungen gefunden, geht es um die Frage, ob alle möglichen Zerlegungen gefunden wurden.
Über die systematische Anordnung der gefundenen Zerlegungen können die Kinder Einsicht in das Entwicklungsprinzip erlangen.
Hier kann die Zweifarbigkeit der Wendeplättchen genutzt werden, um die systematischen operativen Beziehungen stärker zu verdeutlichen:
Erhöht sich die Menge der blauen Plättchen um eins, wird gleichzeitig die Menge der roten Plättchen um eins vermindert.
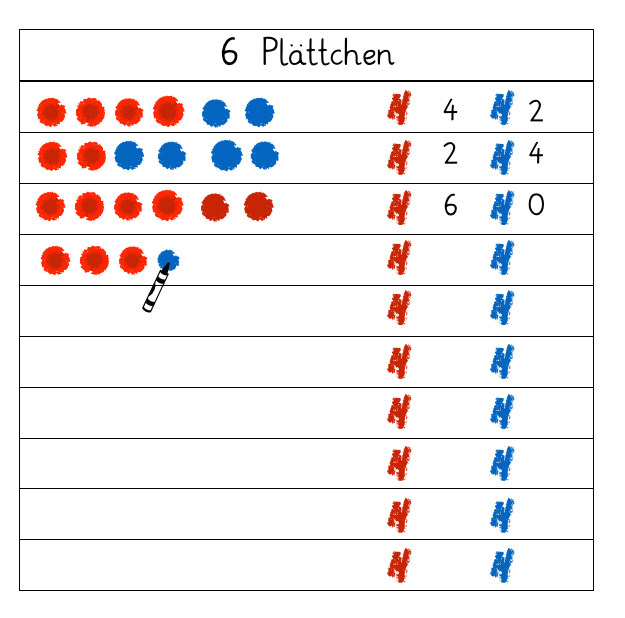Abbildung 10
Die Erkenntnis, dass sich durch Veränderung der einen Teilmenge auch die zweite Teilmenge – vorhersagbar – verändert, ist von grundlegender Bedeutung und muss immer wieder in den Blick genommen werden.
Hierfür ist es wichtig die Kinder anzuregen, ihre Handlungen und Entdeckungen zu verbalisieren und den Blick dabei auf die Strukturen, Beziehungen und Zusammenhänge zu lenken (vgl. Häsel-Weide u.a. 2013).
Zahlzerlegungen finden:
mit Fingerbildern: Auch mit Fingerbildern können Zahlzerlegungen erarbeitet werden, hier bieten sich insbesondere die Zerlegungen der Zahlen 5 und 10 an.
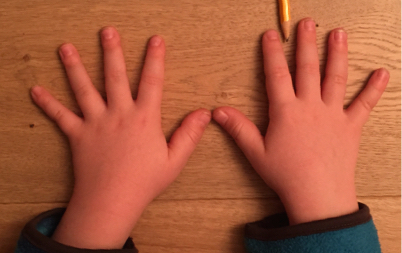Abbildung 11
Zerlegung der Zahl 10 mit Hilfe der Finger: Schipper (2005) zeigt auf, wie beispielsweise die Zerlegung der Zahl 10 mit Hilfe der Finger erfolgen kann.
Immer zwei Kinder arbeiten gemeinsam an den Aufgaben. Ein Kind legt beide Hände auf den Tisch, das Partnerkind legt dann jeweils einen Stift zwischen zwei Finger, so dass sich eine Zerlegung ergibt. Zu Beginn der Übung muss die Leserichtung – von links nach rechts, ausgehend vom Kind, das die Hände auf dem Tisch liegen hat – festgelegt werden.
Das Kind gibt anschließend an, wie viele Finger sich auf der einen Seite des Stiftes und wie viele sich auf der anderen Seite des Stiftes befinden. Es genügt hierbei, wenn ausschließlich die Zahlen genannt werden.
Von fundamentaler Bedeutung für den Aufbau des Teil-Ganzes-Konzeptes ist in diesem Zusammenhang, dass es den Kindern auf Dauer gelingt, sich von der Ebene der konkreten Handlungen zu lösen und Handlungen mental zu vollziehen bzw. zu verinnerlichen.
Zahlzerlegungen automatisieren:
Nach dem Aufbau des Teil-Ganzes-Konzeptes geht es in einem zweiten Schritt um die Automatisierung spezifischer Teil-Ganzes-Beziehungen.
D. h. um Rechenaufgaben nicht-zählend lösen und operative Rechenstrategien flexibel einsetzen zu können, müssen die Kinder zunächst spezifische Beziehungen zwischen Zahlen verstehen, zum anderen müssen bestimmte Zahlentripel automatisiert sein.
Betrachtet man zunächst den Zahlenraum bis 10, dann sind hier neben den Verdoppelungsaufgaben (z. B. 8 – 4 – 4) insbesondere die Beziehungen der Zahlen zur 5 und zur 10 von grundlegender Bedeutung (z. B. Zahlentripel wie 10 – 3 – 7, 5 – 3 – 2 oder auch 9 – 5 – 4).
„Zur Basis für nicht-zählende Lösungsstrategien wird das Teile-Ganzes-Konzept also erst dann, wenn ein bestimmtes, im Sinne von Teilen und Ganzem gedachtes Zahlentripel bereits auch automatisiert ist. Es bedarf, über das grundsätzliche Verständnis von ‚Zahlen als Zusammensetzungen aus anderen Zahlen’ hinausgehend, auch eines bereits automatisierten Wissens darüber, welche spezifischen Zahlen zueinander in diesem Zusammenhang stehen“ (Gaidoschik, 2010a, S. 114, Hervorhebungen im Original).
Beispielaufgabe 4 + 5: Ist das Zahlentripel 9 – 5 – 4 automatisiert, kann die Aufgabe 4 + 5 direkt gelöst werden.
Wird die Aufgabe als 4 + 4 + 1 gedacht, werden andere Zahlentripel aktiviert. So müssen die Kinder hier beispielsweise über das Wissen verfügen, dass die 5 in 4 und 1 zerlegt werden kann, dass 8 die Verdoppelung von 4 ist und dass 9 in 1 und 8 zerlegt werden kann.
Wird der Ansatz über die Aufgaben 5 + 5 – 1 gewählt, wird auf andere Zahlentripel zurückgegriffen (z. B. 10 – 5 – 5 und 10 – 9 – 1).
Insbesondere Kinder mit Lernschwierigkeiten haben jedoch häufig Schwierigkeiten mit der Automatisierung, diese gelingt oft nur verzögert, fragmentarisch oder mit einem hohen Übungsaufwand.
Vor diesem Hintergrund stellt sich die Frage, wie insbesondere Kinder mit Lernschwierigkeiten bei der Automatisierung von Zahlzerlegungen unterstützt werden können.
Aus mathematikdidaktischer Perspektive finden die Kinder eine Unterstützung bei der Automatisierung, wenn einzelne Zerlegungen nicht isoliert auswendig gelernt werden müssen, sondern vielmehr der strukturelle Aufbau der Zahlen als Unterstützungshilfe genutzt werden kann.
Denn nutzen und verstehen Kinder operative Zusammenhänge und Beziehungen zwischen Zahlen, dann gelingt es ihnen auch besser, Zahlzerlegungen zu automatisieren.
2. (An)zahlen vergleichen
Das Bestimmen von sogenannten Differenzmengen ist eine weitere wichtige Fähigkeit, die Kinder während der Grundschulzeit erlernen sollten.
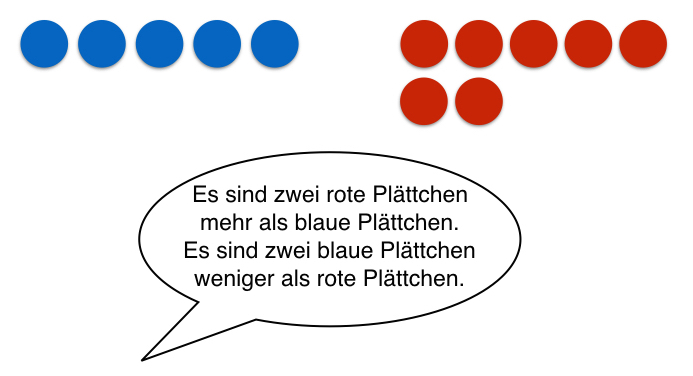Abbildung 18
Hierbei geht es auch um die Erkenntnis, dass beispielsweise die Differenz zwischen den Mengen 5 und 7 ebenso 2 beträgt wie die Differenz zwischen 6 und 8 oder zwischen 8 und 10. Erst auf der Basis dieser Fähigkeit lassen sich Vergleichsaufgaben wie die folgenden erfolgreich bearbeiten:
"Lena hat 5 Kekse, Hans hat 7 Kekse. Wie viele Kekse hat Hans mehr als Lena?" oder
"Lena hat 7 Kekse, sie hat 2 Kekse mehr als Jonas. Wie viele Kekse hat Jonas?"
Bereits im Vorschulalter gelingt es Kindern in der Regel, kleinere Mengen miteinander zu vergleichen und auf der Grundlage ihrer Wahrnehmung die größere bzw. kleinere der beiden Mengen zu bestimmen (mehr / weniger) (vgl. Resnick, 1983; protoquantitative Vergleichsschemata, s.o.).
Um zwei Mengen miteinander zu vergleichen, stehen prinzipiell zwei Wege zur Verfügung. Zum einen kann ein Vergleich über eine Eins-zu-Eins-Zuordnung der Elemente erfolgen, zum anderen über das Abzählen der Elemente.
Wählen Kinder die Strategie des Abzählens, um zwei Mengen miteinander zu vergleichen, kann es vorkommen, dass keine kardinale sondern eine ordinale Sicht auf die Mengen erfolgt und die Mengen nicht direkt miteinander verglichen werden. Der Mengenvergleich erfolgt dann indirekt über die Zahlwortreihe, d.h. die einzelnen Elemente einer Menge werden gezählt, anschließend erfolgt ein Vergleich der Zahlen.
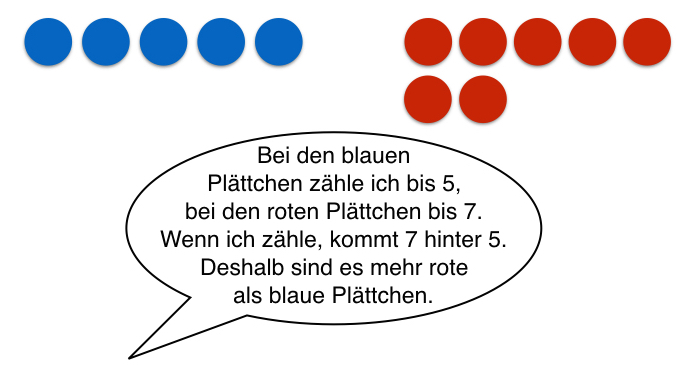Abbildung 19
Wichtig ist es dann, die Kinder bei der Entwicklung einer kardinalen Sicht auf Mengen zu unterstützen und das strukturierte Vergleichen von zwei gegebenen Mengen zu schulen.
Wo sind mehr bzw. weniger Plättchen?
In einem ersten Schritt geht es um das Erkennen von mehr bzw. weniger Plättchen.
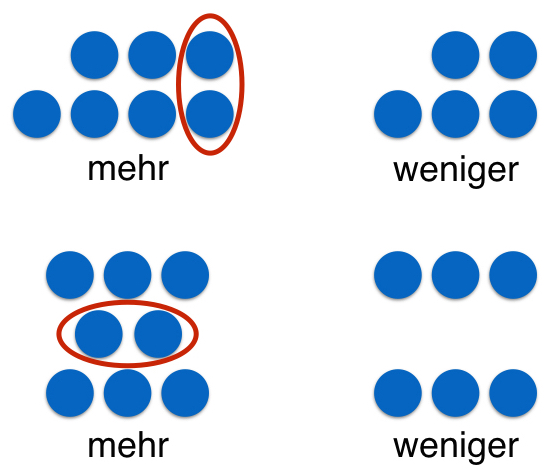Abbildung 20
Vergleich über eine Eins-zu-Eins-Zuordnung:
Ein direkter Mengenvergleich kann auch über eine Eins-zu-Eins-Zuordnung der einzelnen Elemente erfolgen. Hierbei wird jedem Element aus der einen Menge genau ein Element der anderen Menge zugeordnet. Geht die Zuordnung auf, dann enthalten beide Mengen die gleiche Anzahl von Elementen. Kann nicht jedem Element ein Element der anderen Menge zugeordnet werden, dann sind in einer Menge mehr bzw. weniger Elemente als in der anderen Menge.
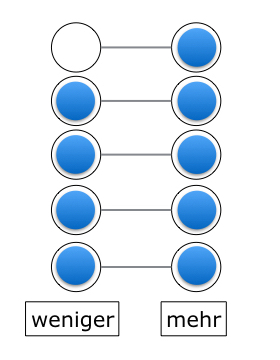Abbildung 21
Anschließend geht es um eine Präzisierung der Begriffe "mehr“ bzw. "weniger“. Hierbei steht die Frage im Mittelpunkt, wie viele Elemente eine der Mengen mehr bzw. weniger hat:
"Wie viel mehr?"
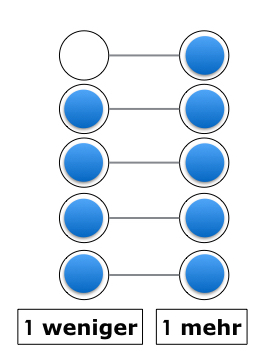Abbildung 22
3. Zahlen positionieren
Werden im mathematischen Anfangsunterricht ordinale Beziehungen zwischen Zahlen in den Blick genommen, geht es in der Regel um die Rangordnung der Zahlen. Bei der Positionierung von Zahlen können beispielsweise Nachbarzahlen (Vorgänger, Nachfolger) oder Nachbarzehner, die relativen Abstände der Zahlen zueinander oder die Position von Zahlen als Mittelzahlen eine Rolle spielen.
Doch wie können Beziehungen zwischen Zahlen, die den ordinalen Zahlaspekt fokussieren, mit Kindern thematisiert und erkundet werden? Welche Möglichkeiten der Veranschaulichung bieten sich hier an?
Eine Möglichkeit, die ersten, eher direkten Vorstellungen der Kinder in Bezug auf ordinale Zahlbeziehungen und strukturelle Zusammenhänge (vgl. Abbildung 2) zu erweitern, bieten Übungen und Aufgabenstellungen an der Zahlreihe.
Die Veranschaulichung des linearen Modells erfolgt in der Grundschule auch durch den Zahlenstrahl. Dieser muss im Unterricht mit den Kindern erarbeitet werden, denn er gilt als zentrales und grundlegendes Anschauungsmittel.
Die Zahlreihe:
"An der Zahlreihe sind sowohl der ordinale als auch der kardinale Zahlaspekt sichtbar: Die Anzahl der Kreise betont die Kardinalzahl, die lineare Anordnung und die geschriebenen Zahlen jedoch die Reihenfolge und damit die Ordinalzahl“ (Scherer & Moser Opitz, 2010, S. 137).
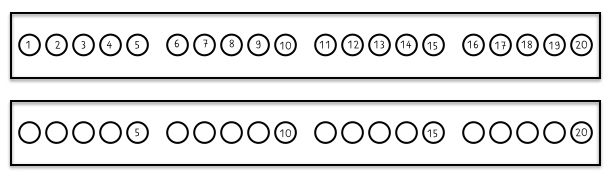Abbildung 23: Die Zahlreihe bis 20
Aufgabenstellungen, bei denen es um die Reihenfolge, die Anordnung und Verortung der einzelnen Zahlen geht, können gut an der Zahlreihe durchgeführt werden. So eignet sich die Zahlreihe beispielsweise zur Bestimmung von Nachbarzahlen (Vorgänger / Nachfolger) oder Nachbarzehnern.
Während sich die Zwanzigerreihe in einigen Schulbüchern findet (vgl. hier z.B. das Zahlenbuch 1), sind sowohl die Hunderter- als auch die Tausenderreihe als Material häufig nicht mehr vorhanden.
Zeigen Kinder beispielsweise Schwierigkeiten bei der Bestimmung von Nachbarzahlen, Nachbarzehnern und -hundertern oder beim Zählen in Schritten im Hunderter- oder Tausenderraum, dann kann es sinnvoll sein, die Zahlreihe bis 100 oder Ausschnitte aus der Zahlreihe bis 1000 als Material herzustellen (vgl. Scherer & Moser Opitz, 2010).
Der Zahlenstrahl:
Im Mathematikunterricht der Grundschule kann der Zahlenstrahl vielfältig eingesetzt werden. Neben dem Ablesen und Einordnen von Zahlen, dem Bestimmen von Nachbarzahlen, Nachbarzehnern und Nachbarhundertern sowie dem Zählen in Schritten ist der Zahlenstrahl von grundlegender Bedeutung für den Umgang mit Größen, mit Messgeräten und Skalen.
Abbildung 24: Der beschriftete Zahlenstrahl
Allerdings ist der beschriftete bzw. durchnummerierte Zahlenstrahl - insbesondere für Kinder mit Lernschwierigkeiten „jedoch von der Sache her komplex und für lernschwache Schülerinnen und Schüler oft schwierig zu verstehen“ (Scherer & Moser Opitz, 2010, S. 138).
Besonders die Verbindung von kardinalen (wie viele?) und ordinalen Deutungen am Zahlenstrahl (der wievielte?) führt oft zu Schwierigkeiten. So stellt sich beispielsweise die Frage, welche Bedeutung die nummerierten Striche und welche Bedeutung die Zwischenräume haben. Sind die nummerierten Striche von Bedeutung oder doch die Zwischenräume? Warum steht die Zahl 2 unter dem dritten Strich des Zahlenstrahls?
Auch Skalierungen können unterschiedlich gedeutet werden. So kann die Beschriftung von zwei identisch aussehenden Zahlenstrahlen verschieden sein.
Trotz dieser Schwierigkeiten ist es wichtig, den Kindern im Mathematikunterricht die Möglichkeit zu geben, die „Skalen von Strahlen in verschiedenen Zahlenräumen zu verstehen und zu erkunden“ (Scherer & Moser Opitz, 2010, S. 144).
Hier kann es verschiedene Zugänge geben.
So können beispielsweise Aktivitäten und Handlungen an der realen und auch ikonisch repräsentierten Zwanziger- bzw. Hunderterkette als Ausgangspunkt für die Arbeit mit dem leeren bzw. teilweise beschrifteten Zahlenstrahl dienen (vgl. Höhtker & Selter, 1995; Scherer & Moser Opitz, 2010).
Eine Hunderterkette besteht bspw. aus einer Anordnung von roten und blauen Perlen. Im Wechsel sind immer 5 bzw. bei der Hunderterkette 10 rote und 10 blaue Perlen aufgereiht. Auf diese Weise wird die dekadische Struktur unseres Zahlsystems betont.
Abbildung 25: Hunderterkette (Ausschnitt)
Von der Hunderterkette zum leeren Zahlenstrahl:
Zunächst geht es um die Erarbeitung der Struktur der Hunderterkette. In einem ersten Schritt wird der Aufbau der Kette in den Blick genommen:
"Wie viele Perlen gibt es insgesamt?"
"Wie kann die Gesamtzahl der Perlen schnell ermittelt werden?"
"Warum gibt es unterschiedlich farbige Perlen?"
"Wie viele Perlen einer Farbe sind immer hintereinander angeordnet etc.."
In einem zweiten Schritt werden Orientierungsübungen an der realen Hunderterkette durchgeführt.
Grundlegend können zwei verschiedene Aufgabentypen unterschieden werden, bei denen es jeweils um die Verortung der Zahlen geht.
Zum einen gibt es die Möglichkeit, eine Position an der Hunderterkette vorzugeben und die entsprechende Zahl angeben zu lassen:
"Welche Zahlenkarte gehört an diese Stelle / Position?“.
Zum anderen können Zahlen (Zahlenkarten) an der Hunderterkette positioniert werden:
"Wohin gehört die Zahlenkarte?“ (vgl. Höhtker & Selter, 1995).
Wichtig ist, dass während der ersten Orientierungsübungen mit den Kindern die Verortung der Zahlenkarten besprochen wird, denn die Karte wird zwischen zwei Kugeln positioniert und die Zahl auf der Karte bezieht sich jeweils auf die Anzahl der Kugeln die sich vor der Zahlenkarte befinden.
Abbildung 26
Im Anschluss an die Orientierungsübungen an der konkreten Hunderterkette können die Orientierungsübungen auch an der ikonisch repräsentierten Hunderterkette durchgeführt werden. So kann die Arbeit am leeren Zahlenstrahl vorbereitet werden.
Abbildung 27
Höhtker und Selter (1995, S. 130) erläutern diesbezüglich, dass "erste Aktivitäten an der als Kette ohne Perlen eingeführten Anschauungshilfe [...] die Parallelisierung dieser beiden Darstellungen zum Ziel [haben]“.
Abbildung 28
Alle Übungen, die an der Hunderterkette durchgeführt wurden, können auch am leeren Zahlenstrahl durchgeführt werden. Gibt es Schwierigkeiten bei der Positionierung der Karten, kann zunächst noch auf die (reale oder ikonisch repräsentierte) Hunderterkette zurückgegriffen werden.
Ist der leere Zahlenstrahl erst einmal eingeführt, kann er – aufgrund seiner Offenheit und prinzipiellen Mehrdeutigkeit – im Mathematikunterricht vielfältig eingesetzt werden.
"Seine Stärke als Denkwerkzeug entfalten und letztlich eine Vielzahl an Beziehungen und die strukturelle Ähnlichkeit der Zahlenräume verdeutlichen“ (Ruwisch, 2015, S. 42) kann der leere Zahlenstrahl allerdings erst dann, wenn bspw. bei Zuordnungsübungen Zahlen nicht einfach an einem festen Platz verortet werden, sondern wenn die Kinder sich Gedanken machen über die Anordnung der Zahlen sowie die Abstände zwischen ihnen, so dass die relativen Abstände der Zahlen zueinander Beachtung finden. Erst dann kann die Ablösung von einer direkten (ordinalen) Zahlvorstellung gelingen.
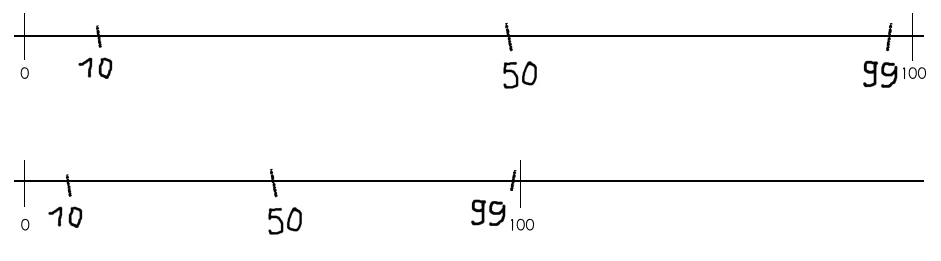Abbildung 29
