Zahlaspekte
In der Mathematik werden verschiedene Zahlaspekte unterschieden, die die vielfältigen Verwendungsarten natürlicher Zahlen beschreiben.
Für den Aufbau tragfähiger Zahlvorstellungen im Anfangsunterricht und somit für die Prävention von Rechenschwierigkeiten und die Entwicklung flexibler Rechenstrategien ist insbesondere die Entwicklung einer kardinalen Zahlvorstellung wesentlich. Auf dieser basiert die Fähigkeit zur strukturierten Anzahlerfassung, d.h. die Fähigkeit, auch größere Anzahlen von Elementen einer Menge bestimmen zu können, ohne diese einzeln zählen zu müssen.
Den ersten und elementarsten Zugang zur Anzahlbestimmung bei größeren Mengen stellt jedoch das Zählen, d.h. die Zuweisung von Zahlen zu Objekten gemäß der Ordnung der Zahlwortreihe dar.
„Die Einsicht, dass gezählt werden muss, um eine Anzahl zu bestimmen, ist ein erster Erkenntnisschritt zum kardinalen Verständnis. Für den Aufbau des Anzahlbegriffes ist es wichtig, dass die Kinder vielfältige Zählerfahrungen machen und in verschiedenen Kontexten zur Anzahlbestimmung aufgefordert werden“ (Häsel Weide et al., 2013, S. 50).
Es zeigt sich, dass sich ein kardinales Zahlverständnis nicht ohne Bezug zur Zahl als Zählzahl und zur Idee der Ordnungszahlen entfalten lässt. Gleichzeitig kann eine kardinale Zahlvorstellung oder die Beschäftigung mit strukturierten Zahldarstellungen beispielsweise das Zählen in Schritten provozieren und so die Flexibilisierung und Weiterentwicklung von Zählstrategien unterstützen.
Der Aufbau kardinaler und ordinaler Zahlvorstellungen bedingt sich somit gegenseitig und ist unmittelbar aufeinander bezogen (vgl. Häsel Weide et al., 2013; Krajewski & Schneider, 2009; Wittmann & Müller, 2009).
Kardinalzahl und Ordinalzahl
Der Kardinalzahl- oder auch Anzahlaspekt nimmt eine Menge von Elementen in den Blick. Zahlwörter können Mengen repräsentieren, mit ihnen kann die Anzahl von Elementen angegeben werden.
Der Ordinalzahlaspekt wird unterschieden in den Zählzahlaspekt (Folge der Zahlen, die beim Zählen durchlaufen wird) und in den Ordnungszahlaspekt.
Ordnungszahlen geben den Platz eines Elementes in der Zahlwortreihe an (z.B. das sechste Plättchen in der Reihe, die Zahl 6 ist Vorgänger der Zahl 7 und Nachfolger der Zahl 5).
Eine Darstellung aller Zahlaspekte (neben dem Kardinal- und Ordinalzahlaspekt wird in der Regel noch zwischen Maßzahlaspekt, Operatoraspekt und Rechenzahlaspekt unterschieden) findet sich beispielsweise in Krauthausen & Scherer (2007) oder in Radatz & Schipper (1999).
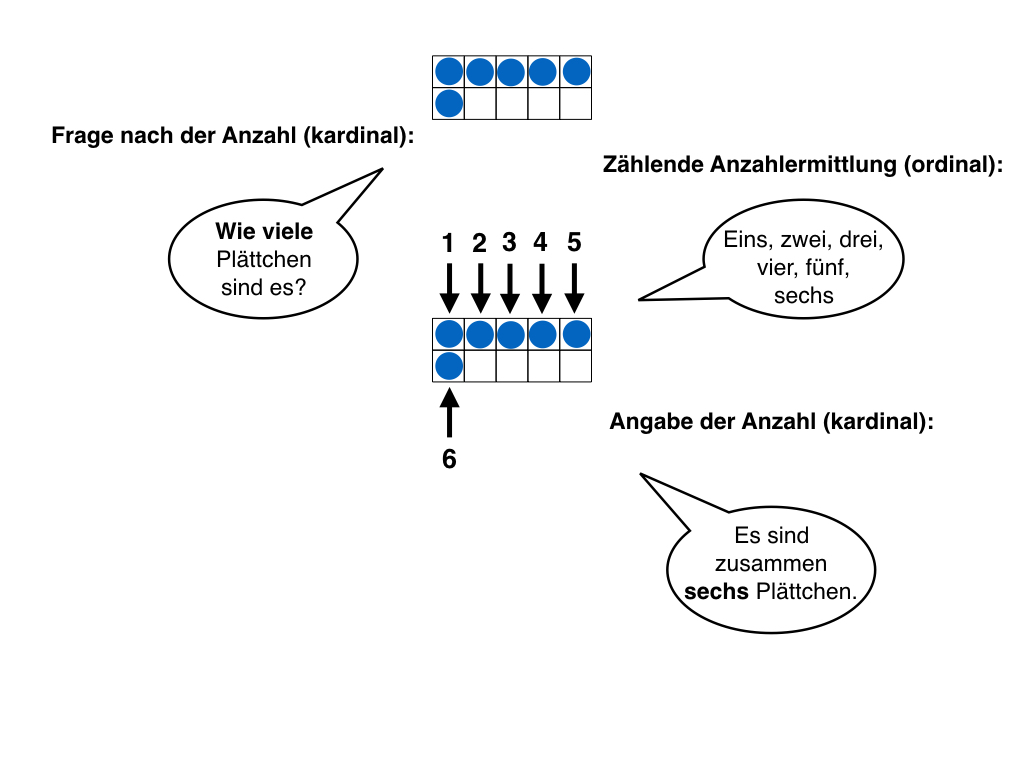
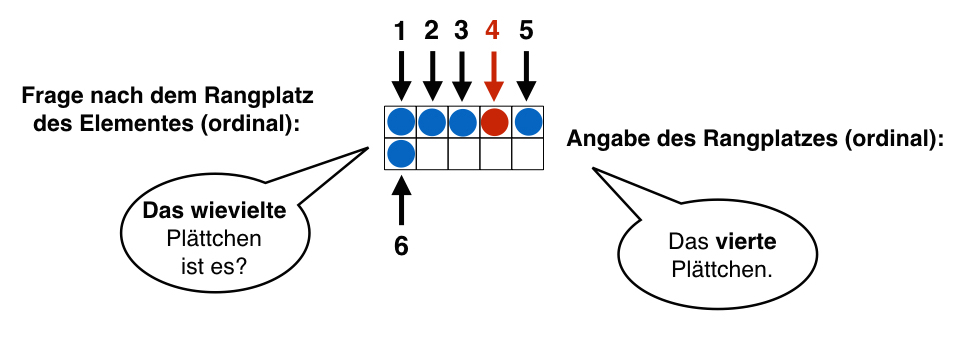 Abbildung 1
Abbildung 1
Zählen als grundlegender Baustein der mathematischen Entwicklung
Die Fähigkeit des Zählens ist somit ein grundlegender Baustein in der mathematischen Entwicklung und bedeutsam während der gesamten Grundschulzeit.
Doch was bedeutet es genau, erfolgreich zählen zu können, und über welche Kompetenzen müssen Kinder verfügen, damit Zählprozesse gelingen?
Welche Schwierigkeiten können in Zählprozessen auftreten und wie kann die Entwicklung flexibler Zählstrategien gefördert und unterstützt werden?
Diesen Fragen wird im Folgenden nachgegangen.
Gelingende Zählprozesse
Obwohl die Fähigkeit, zählen zu können, auf den ersten Blick eher unkompliziert erscheint, wird bei näherer Betrachtung von Zählprozessen schnell deutlich, dass sich hinter der Tätigkeit des Zählens komplexe Anforderungen verbergen.
Bereits früh – im Alter von 2 bis 3 Jahren beginnen Kinder ihre Umgebung (auch) zählend zu erkunden. Fragt man Kinder in diesem Alter, ob sie schon zählen können, dann nennen sie oft eine Abfolge von Zahlen, sie versuchen, die korrekte Folge der Zahlwortreihe zu reproduzieren (vgl. Mack, 2005).
Um aber Mengen von Elementen erfolgreich abzählen zu können, müssen Kinder nicht nur die korrekte Folge der Zahlwörter kennen, sie müssen darüber hinaus über weitere Kompetenzen verfügen. Wesentlich für den Aufbau von Zählkompetenz ist die Einsicht in verschiedene Zählprinzipien.
Zählprinzipien
-
Prinzip der stabilen Rangfolge: Die Reihenfolge der Zahlwörter bleibt immer gleich, d.h. dass beim Zählprozess immer die gleiche Folge an Zählzahlen durchlaufen wird.
-
Eins-Eins-Prinzip: Man spricht von einer Eins-zu-Eins-Zuordnung, wenn jedem Element genau ein anderes Element, genau ein Zahlwort zugeordnet wird. Das bedeutet, dass keines der Elemente doppelt gezählt und keines der Elemente vergessen werden darf.
-
Kardinalprinzip: Beim Abzählen einer Menge von Elementen gibt das zuletzt genannte Zahlwort die Gesamtzahl der Elemente an, d.h. das zuletzt genannte Zahlwort ist die Antwort auf die Frage: "Wie viele?“.
-
Prinzip der Irrelevanz der Reihenfolge: Sowohl die Reihenfolge, in der die Elemente einer gegebenen Menge gezählt werden, als auch die Anordnung der Elemente ist für das Ergebnis des Zählprozesses irrelevant. Der Zählprozess kann bei einem beliebigen Objekt beginnen.
-
Abstraktionsprinzip: Die zuvor genannten Prinzipien sind auf beliebige Elemente anwendbar. Sowohl konkrete Materialien aber auch Töne, Lichtsignale etc. sind zählbar. Die Objekte, die gezählt werden, müssen dabei nicht in einem inhaltlichen Zusammenhang stehen (vgl. Gelman & Gallistel, 1978).
Zählkompetenzen von Schulanfängern
Bereits mit Schuleintritt verfügen viele Kinder über vielfältige arithmetische Fähigkeiten. Sie bringen Kenntnisse mit, die von Lehrkräften zuweilen sogar unterschätzt werden. Gleichwohl gilt dies nicht für alle Kinder am Schulanfang. Vielmehr sind die Fähigkeiten und Kenntnisse der Schulanfänger ausgesprochen heterogen (vgl. Krauthausen & Scherer, 2007; Schipper, 1998).
Es gibt zum einen Kinder, die bereits fehlerfrei über 100 zählen können, auf der anderen Seite gibt es Schulanfänger, die noch Schwierigkeiten mit der Zahlwortreihe bis 10 haben, die noch nicht von einer vorgegebenen Zahl aus weiterzählen oder rückwärts zählen können (vgl. Gasteiger, 2011). Zudem muss in Bezug auf Kinder mit Lernschwierigkeiten beachtet werden, dass diese in der Regel „über geringere Zählkompetenzen verfügen als Kinder ohne Schwierigkeiten [...]“ (Scherer & Moser Opitz, 2010, S. 115).
Generell gilt, dass Kinder lernen zu zählen, indem sie zählen, d.h. indem sie immer wieder die Gelegenheit erhalten, ihre Zählkompetenz zu trainieren. Kindern mit Lernschwierigkeiten, mit fehlenden oder eingeschränkten Zählerfahrungen müssen die Gelegenheit erhalten, in der Schule grundlegende Zählerfahrungen zu machen.
Der Aufbau von Zählkompetenz „muss [...] im Unterricht besonders berücksichtigt werden, insbesondere auch, weil Zählen kulturell vermittelt wird und Kinder mit dem Zählen beginnen, wenn sie es von Eltern, Geschwistern oder anderen Personen in ihrem Umfeld hören. Mangelnde Zählkompetenz kann somit auch mit fehlenden Erfahrungen zusammenhängen“ (Scherer & Moser Opitz, 2010, S. 115).
Förderung von Zählkompetenzen
Verbales Zählen
Verbales Zählen beschreibt die Fähigkeit, die Zahlwörter in der korrekten Abfolge wiedergeben zu können.
Fuson entwickelte bereits 1988 ein Modell, welches den Erwerb der Zahlwortreihe in den Blick nahm. Sie zeigt auf, dass es zwischen der Auffassung der Zahlwortreihe als Ganzheit, bei der die einzelnen Zahlwörter noch nicht als abgrenzbare Einheit wahrgenommen werden – die Zahlwortreihe ist hier vergleichbar mit einem auswendig beherrschten Lied oder Gedicht – und dem flexiblen und sicheren Gebrauch der Zahlwortreihe verschiedene Ebenen der Entwicklung gibt, auf denen sich Kinder befinden können (vgl. hierzu Fuson, 1988; Gasteiger, 2011).
Wichtig im Anfangsunterricht ist zunächst das Lernen der Zahlwortreihe bis 20. In der Folge müssen dann die Zahlwörter für die Zehnerzahlen erfasst werden. "Das Kind kombiniert diese Zahlen miteinander und konstruiert so selbst den Rest der Zahlwortreihe [...]. Dabei kommt es häufig zu ‚logischen Verzählungen‘ oder Fehlbenennungen wie ‚zehnundzwanzig‘ für 30, ‚zehnzig‘ für 100“ (Schmassmann & Moser Opitz, 2008, S. 13).
Im deutschen Sprachraum werden viele Zahlwörter nicht konsistent gebildet. Diese Inkonsistenzen sowie weitere Unregelmäßigkeiten bei der Aussprache der Zahlwörter (so wird beispielsweise bei den Zahlen ab 13 zuerst der Einer und dann der Zehner genannt, während von 101 an zuerst der Hunderter und dann Einer und Zehner genannt wird), erschweren zusätzlich das Erlernen der Zahlwortreihe (vgl. Krauthausen & Scherer, 2007; Scherer & Moser Opitz, 2010).
Das Aufsagen und Lernen der Zahlwortreihe wird in der Schule oft durch Klatschen oder andere Bewegungen begleitet. Allerdings muss die Verbindung von verbalem Zählen und Bewegungen im Vorfeld genau überlegt werden, denn sie ist nicht immer hilfreich. Für viele Kinder stellt die Begleitung von Zählprozessen durch rhythmische Bewegungen eher eine zusätzliche Herausforderung dar (vgl. Scherer & Moser Opitz, 2010). Nur dann, wenn die Kinder bereits von sich aus Zählprozesse mit Bewegungen begleiten – hier ist eine gute Beobachtung wichtig – sollten sie hierbei unterstützt werden.
Vertiefende Anregungen, Ideen und Übungen zur Sicherung der Zahlwortreihe finden Sie unter Unterricht: Zahlwortreihe.
Zählen von Objekten und Förderung des kardinalen Verständnisses
Durch Zählübungen, bei denen das Zählen von Objekten im Vordergrund steht, soll die Einsicht in die Zählprinzipien vertieft und unterstützt werden (s.o.).
Grundsätzlich sollte Wert gelegt werden auf Zählaktivitäten, die von den Kindern auch als interessant und sinnvoll erlebt werden. Wichtig ist hier auch immer wieder die Förderung des kardinalen Verständnisses durch die Frage: „Wie viele sind es zusammen?“
Übungen zum verbalen Zählen und zur Anzahlermittlung sollten zudem immer wieder miteinander verbunden werden – es geht hier um die Bedeutung und den Sinn von Zählaktivitäten. Die Kinder müssen verstehen, dass wir zählen, um Anzahlen zu bestimmen und nicht, um einfach eine Folge von Zahlen aufzusagen. Sehr wichtig ist es, die Kinder immer wieder anzuregen, über Zählprozesse nachzudenken und zu sprechen.
Vertiefende Anregungen, Ideen und Übungen zur Anzahlermittlung finden Sie unter Unterricht: Zählen von Objekten.