Abbildung 1: Grundlegendes Üben
Ein wesentliches Ziel des grundlegenden Übens ist es, Zahl- und Operationsvorstellungen aufzubauen, indem Handlungen oder Bilder mit Unterstützung von geeigneten Materialien und sprachlichen Mitteln zu gedanklichen Vorstellungen umgebaut werden.
Grundvorstellungen und Rechenschwierigkeiten
Egal mit welchem mathematischen Inhalt sich die Lernenden beim Üben beschäftigen sollen, der Aufbau tragfähiger Grundvorstellungen bildet die Basis für weitere Lernprozesse. Nicht selten wird aber – gerade bei Kindern mit Schwierigkeiten im Mathematiklernen – der Fokus auf „Kenntnis und Anwendung von ausgewählten Rechenverfahren und das mechanische Aufsagen von mathematischen Fakten“ (Häsel-Weide, Nührenbörger, Moser Opitz & Wittich, 2013, 31) gelegt, in der vermeintlich guten Absicht, diese Kinder nicht zu überfordern (ebd.). Allerdings sind eingeschränkte oder fehlerhafte Zahl- und Operationsvorstellungen bei Rechenschwierigkeiten häufig zu beobachten (Gaidoschik, 2006). Außerdem ist der Aufbau von flexiblen Rechenfähigkeiten auf tragfähige Zahl- und Operationsvorstellungen angewiesen (Götze, Selter & Zannetin, 2019).
Zahlvorstellungen
Kinder mit Rechenschwierigkeiten fehlen häufig tragfähige Zahlvorstellungen. Es ist jedoch zentral, dass sie „Zahlen in Relation zueinander deuten lernen“ (Häsel-Weide, Nührenbörger, Moser Opitz & Wittich, 2013, 51) Diesen Kindern fehlt „oft die Erkenntnis, dass sich Zahlen wiederum aus anderen Zahlen zusammensetzen“ (ebd.), der Teil-Ganzes-Aspekt ist aber entscheidend für das Erkennen und Nutzen von Nachbarzahlen und Hilfsaufgaben. Daran schließt sich die Erkenntnis an, dass sich eine zusammengesetzte Menge auch nicht verändert, wenn insgesamt nichts hinzugefügt oder weggenommen wird, man also einen Teil wegnehmen und ihn an anderer Stelle wieder hinzufügen kann (ebd.). Das gegen- oder gleichsinnige Verändern (Konstanz der Summe) fußt auf dieser Grundvorstellung. „Gerade im Hinblick auf die Multiplikation und Vision ist die Zerlegung einer Zahl in eine Anzahl gleichmächtiger Teilmengen relevant“ (ebd., S. 58).
Operationsvorstellungen
Auch bezogen auf arithmetische Operationen zeigen Kinder mit Rechenschwierigkeiten häufig unzureichende Vorstellungen (ebd.). Addition und Subtraktion beispielsweise werden oft ausschließlich „als ‚rauf‘ und ‚runter‘ beziehungsweise vorwärts und rückwärts auf der Zahlenreihe verstanden“ (ebd., 53). Eine solche (auf dem Ordinalzahlaspekt beruhende) Vorstellung lässt nur eine (ab-)zählende Lösungsstrategie zu, was spätestens dann zu Problemen führt, wenn der Zahlenraum größer wird (Gaidoschik, 2006). Nicht zuletzt verschließt diese Vorstellung den Blick vor möglicherweise hilfreichen Tausch-, Nachbar- oder Umkehraufgaben.
Analog dazu haben Kinder zur Multiplikation oft nur die Vorstellung, etwas wiederholt zu tun. Die Aufgabe 3 • 4 interpretieren sie dann ausschließlich als zeitlich-sukzessive Addition, zum Beispiel als wiederholte Handlung: „Ich esse jeden Tag 4 Bonbons. Wie viele Bonbons esse ich an 3 Tagen?“. Weitere zentrale Grundvorstellungen, wie das (räumlich-simultane) Zusammenfassen: „In einem Getränkekasten stehen 3 Reihen mit jeweils 4 Flaschen. Wie viele Flaschen sind es insgesamt?“ oder das Vergleichen: „Ich habe 4 Bonbons. Du hast 3mal so viele wie ich. Wie viele sind das?“ sind aber für das flexible Rechnen und das Erkennen von Rechengesetzen bei der Multiplikation zentral (siehe hierzu auch Vernetzendes Üben). Die Operationsvorstellungen zur Multiplikation sollten deshalb um diese zentralen Grundvorstellungen erweitert werden (Götze, Selter & Zannetin, 2019).
Zahl- und Operationsvorstellungen sind außerdem vielfältig miteinander verknüpft. Auf der einen Seite können, wie oben beschrieben, unzureichende Zahlvorstellungen den Aufbau von Operationsvorstellungen hemmen: Eine ausschließlich auf dem Ordinalzahlaspekt beruhende Zahlvorstellung lässt bei der Aufgabe 7 - 3 nur eine (ab-)zählende Lösungsstrategie zu (Abb. 2).
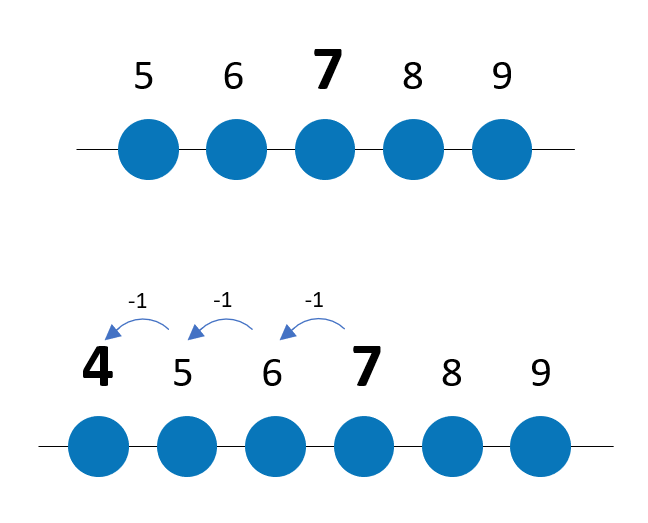Abbildung 2: Auf dem Ordinalzahlaspekt fußende Vorstellung der Subtraktion (7 - 3 = 4)
Auf der anderen Seite haben die Entwicklung neuer Vorstellungen das Potential, bestehende Vorstellungen zu erweitern. Die Vorstellung der Multiplikation als räumlich-simultanes Zusammenfassen birgt beispielsweise die Chance, Zahlen als Produkt zweier Faktoren sehen zu können (Abb. 3).
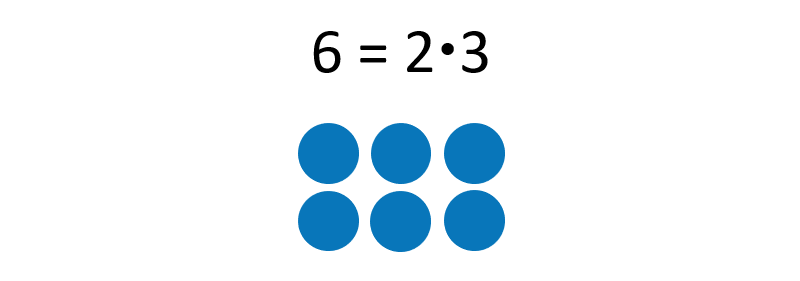Abbildung 3: Die "6" als Produkt aus "2" und "3" und somit als gerade Zahl
Die Zahl 6 kann dann als Produkt aus 2 und 3 gesehen werden, wobei die bildliche Darstellung dieser Vorstellung die 6 als gerade Zahl erkennbar macht: sie kann durch zwei Reihen mit genau gleich vielen Elementen dargestellt werden.
Gerade weil Kinder mit Lernschwierigkeiten oftmals unzureichende Zahl- und Operationsvorstellungen entwickeln, profitieren sie besonders von einem Unterricht, der auf deren Aufbau achtet und genügend Zeit dazu lässt.
Grundvorstellungen aufbauen
Ausführliche Hinweise und Aufgaben zum Aufbau von Zahl- und Operationsvorstellungen finden sich auf dieser Seite in den Bereichen Inhalte – Zahlvorstellungen und Inhalte – Operationsvorstellungen. An dieser Stelle folgt ein kurzer Überblick über die für das Grundlegende Üben wichtigsten Aspekte.
Darstellungswechsel
Die Fähigkeit zum Darstellungswechsel ist wesentlich für den Aufbau tragfähiger Zahl- und Operationsvorstellungen (Selter & Zannetin, 2019). Zahlen oder Operationen können durch Handlungen mit Material, Bilder, gesprochene oder geschriebene Sprache oder symbolische Darstellungen (Mathesprache) repräsentiert werden.
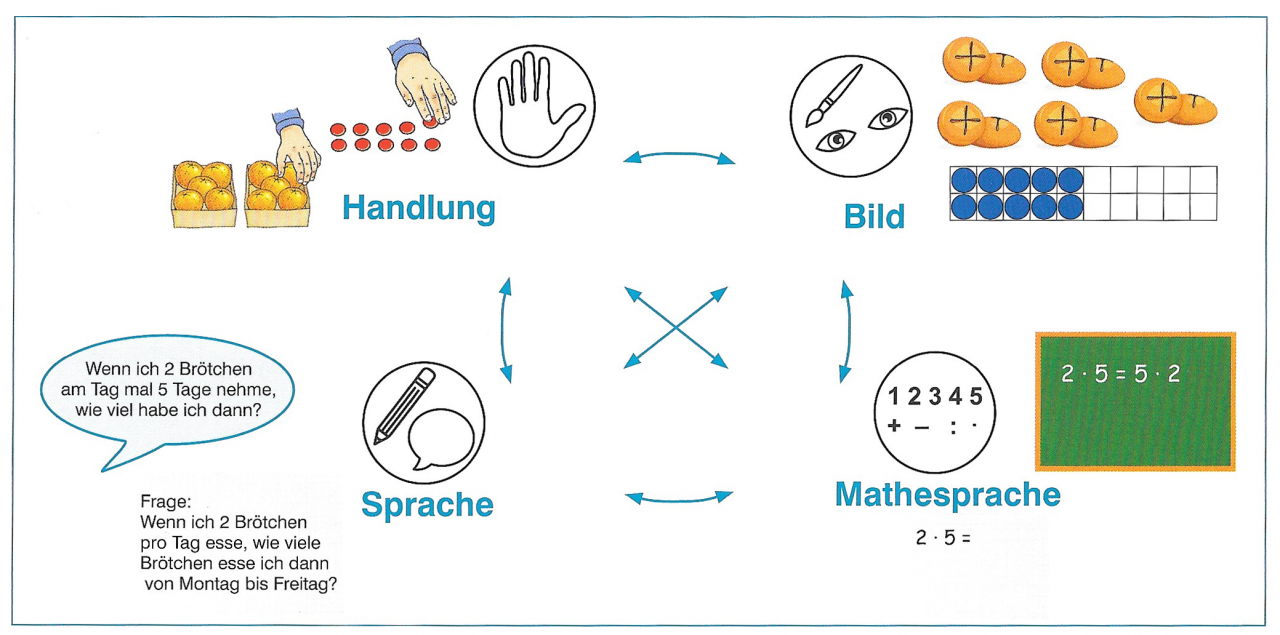Abbildung 4: Darstellungsformen (Selter & Zannetin, 2019, 46)
Die Darstellungsmöglichkeiten sollen dabei nicht nur in einer Richtung von konkret zu abstrakt durchlaufen werden, um am Ende die formale Mathesprache zu nutzen. Ziel ist es, die Darstellungsformen miteinander zu vernetzen und flexibel zwischen ihnen übersetzen zu können - auch, aber nicht ausschließlich, um symbolische Darstellungen lebendig halten zu können (ebd., 32). Dies gelingt besonders dann, wenn Darstellungen nicht einfach zugeordnet, sondern der Wechsel sprachlich begleitet und begründet wird.
Material
Kinder müssen es sich aktiv erarbeiten, „konkretes Material zunehmend in seiner Funktion als Repräsentation mathematischer Strukturen“ (Söbbeke, 2008, 3) sehen und nutzen zu können. Die Fähigkeit dazu ist anspruchsvoll, stellt aber gleichzeitig eine „fundamentale Basiskompetenz des mathematischen Denkens insgesamt dar“ (ebd.) und ist deshalb für alle Kinder elementar. Für Kinder mit Schwierigkeiten in Mathematik sind besonders zwei Aspekte bedeutsam:
-
„Sparsamkeit ist insbesondere für schwächere Schülerinnen und Schüler hilfreich, da jedes neue Material eine eigene Fremdsprache darstellt, in die die arithmetischen Operationen übertragen, übersetzt werden müssen“ (Lorenz, 2000, S. 21).
-
Das Material sollte sich dazu eignen, Lernprozesse langfristig anzulegen, also auf einem höheren Niveau erweitert zu werden (z.B. 10er-Feld bzw. 10er-Streifen à 20er-Feld à 100er-Feld). So kann mit gleichem oder ähnlichem Material im Sinne des Spiralprinzips in unterschiedlichen Lernphasen immer wieder gearbeitet werden (Selter & Zannetin, 2019).
Sprache
Ähnlich wie bei der Auswahl von Anschauungsmitteln darauf geachtet werden sollte, dass sie mathematische Strukturen gut repräsentieren, sollten auch Versprachlichungen von mathematischen Inhalten den Aufbau angemessener Grundvorstellungen zu unterstützen. Sprachmittel sind dann besonders hilfreich, wenn sie explizit Bedeutung transportieren und dabei die kognitive Funktion von Sprache unterstützen (Prediger, 2019), also tatsächlich „Denkwerkzeuge für neue Denkhandlungen“ (ebd., 251) sind.
Ein Beispiel: Beim Aufbau von Operationsvorstellungen zur Multiplikation ist von Bedeutung, dass die Lernenden zwischen Multiplikand („Wie viele in einer Gruppe bzw. Reihe?“) und Multiplikator („Wie viele Gruppen bzw. Reihen?“) gedanklich unterscheiden können. Das Sprachmittel „drei mal sechs“ repräsentiert diese Unterscheidung nicht explizit, „drei Sechser“ schon.
Das Vierphasenmodell: vom konkreten zum gedanklichen Handeln
„Die Grundidee beim Aufbau von Grundvorstellungen ist, dass konkrete Handlungen an geeigneten Materialien zu gedanklichen Operationen umgebaut werden“ (Wartha & Schulz, 2011, 11). Dieser Prozess der Verinnerlichung läuft nicht automatisch ab, besonders leistungsschwächere Kinder benötigen hierbei Unterstützung. Das Vierphasenmodell zeigt, wie „der Prozess vom konkreten zum gedanklichen Handeln“ (ebd., Hervorhebung i. O.) unterstützt werden kann.
"Das Vierphasenmodell"
(Wartha & Schulz, 2011, 11)
Phase 1: Das Kind handelt am geeigneten Material.
Die mathematische Bedeutung der Handlung wird beschrieben. Zentral: Versprachlichen der Handlung und der mathematischen Symbole.
Phase 2: Das Kind beschreibt die Materialhandlung mit Sicht auf das Material.
Es handelt jedoch nicht mehr selbst, sondern diktiert einem Partner die Handlung und kontrolliert den Handlungsprozess durch Beobachtung.
Phase 3: Das Kind beschreibt die Materialhandlung ohne Sicht auf das Material.
Für die Beschreibung der Handlung ist es darauf angewiesen, sich den Prozess am Material vorzustellen.
Phase 4: Das Kind arbeitet auf symbolischer Ebene, übt und automatisiert.
Gegebenenfalls wird die entsprechende Handlung in der Vorstellung aktiviert.
Zum Arbeiten mit dem Vierphasenmodell gibt es auf dieser Seite im Bereich Leitideen – Diagnosegeleitet fördern zwei Beispielvideos.
Grundvorstellungen aufbauen im Übungsprozess
Für den Unterricht lassen sich sowohl aus dem Vierphasenmodell (Wartha & Schulz, 2011) als auch aus der Forderung nach dem Wechsel zwischen den Darstellungsformen zahlreiche Übungsaufgaben ableiten, die nicht nur den Aufbau von Grundvorstellungen unterstützen, sondern auch Aufschluss über den individuellen Entwicklungsstand der Kinder geben („In welcher Phase im Vierphasenmodell bewegt sich der/die Lernende bereits sicher?“, „Welche Übersetzung zwischen welchen Darstellungen gelingt noch nicht sicher?“).
Gleichzeitig kann auch schon sichtbar werden, inwiefern es den Lernenden gelingt, Beziehungen zwischen Zahlen oder Aufgaben zu erkennen. Fällt einem Kind etwa auf, dass im Punktebild von 3 6 auch die Aufgabe 6 3 gesehen werden kann? Oder erkennt ein anderes, dass sich die 5 sowohl als 3 und 2, als auch als 4 und 1, legen lässt, wenn man nur ein Plättchen verschiebt oder umdreht?
Es wird deutlich, dass das grundlegende Üben nicht nur die die Basis für das vernetzende Üben darstellt, sondern auch eng mit diesem verknüpft ist, wobei die über das Material, die Handlung oder die Sprache gestützten Vorstellungen das verbindende Element darstellen. Aus diesem Grund ist es für den Lernprozess wesentlich, in beiden Übungsphasen passende Darstellungs- und Sprachmittel zu benutzen. Im Teilmodul „Unterricht“ werden Anregungen gegeben, wie der Aufbau von Grundvorstellungen unterstützt werden kann.
