Für den Aufbau von Grundvorstellungen ist eine Vielzahl an unterschiedlichen Aufgabenformaten denkbar. Zum mathematisch-inhaltlichen Fokus dieses Teilmoduls – dem effektiven Aufbau von Operationsvorstellungen zur Multiplikation – gibt es einige spielerische Zugänge, z.B. die Lernumgebung „Pasch würfeln“ auf dieser Seite, das „Malquartett“ auf PIK AS oder das „Mal-Trio“ auf PIK AS kompakt.
Für dieses Teilmodul illustriert das „Mal-Memory“ den spielerischen Aufbau von Grundvorstellungen. Es versteht sich als für den inklusiven Unterricht angepasste Adaption der zuletzt genannten Lernumgebungen. Dabei werden die im Hintergrundteil beschriebenen Hinweise für das Grundlegende Üben im inklusiven Unterricht beispielhaft umgesetzt.
Lernumgebung „Mal-Memory“
Kernidee ist das Memory-Spiel, bei dem zwei passende Karten, in diesem Fall zwei Darstellungsformen derselben Einmaleins-Aufgabe, gefunden werden sollen.
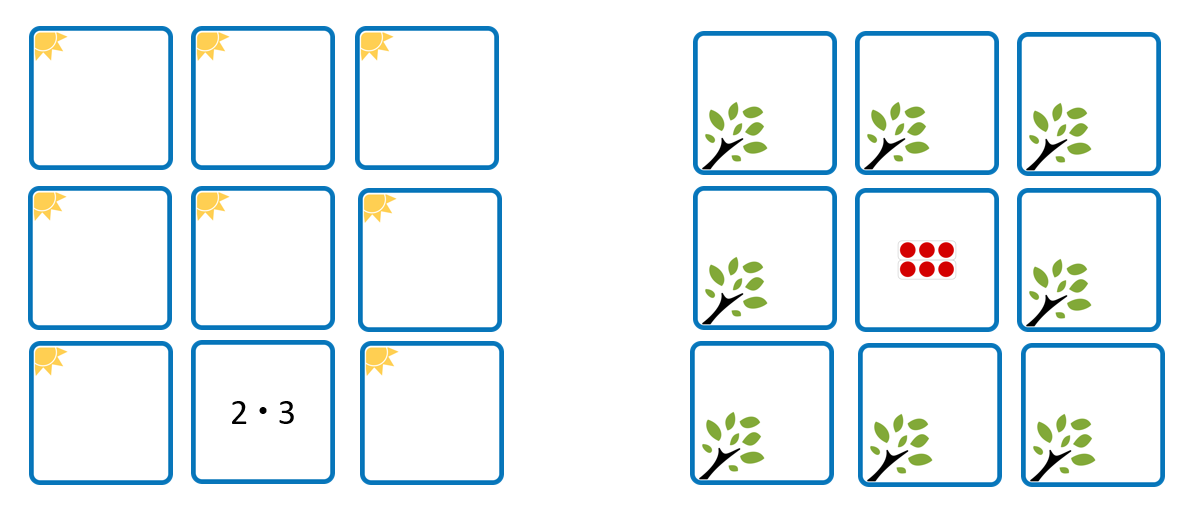
In diesem Beispiel wurde auf der linken Seite die symbolische Darstellung, auf der rechten Seite die Darstellung als vorgegebenes Punktebild. Es sind aber auch andere Darstellungsformen denkbar (s.u.). Entscheidend ist, dass die Lernenden ihre Spielzüge sprachlich begleiten und dabei Begründungen für eine Passung / keine Passung formulieren.
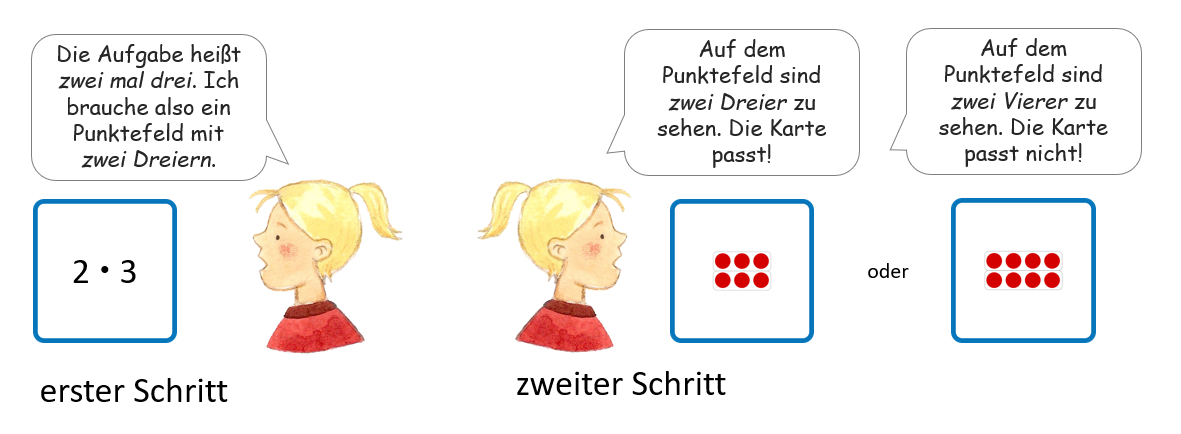
Die Lernenden decken zunächst eine Karte auf, beschreiben sie und formulieren, was auf der dazu passenden Karte zu sehen sein müsste. Erst dann wird die zweite Karte aufgedeckt, auch sie wird beschrieben, und dann wird entschieden, ob sie passt. Beim Formulieren, was auf der passenden Karte zu sehen sein müsste, werden die Kinder dazu angeregt, sich diese gedanklich vorzustellen. Auf dem „Vier-Phasen-Modell“ (Wartha & Schulz, 2011,11) lässt sich dieser Handlungsschritt der Phase 3 zuordnen. Das Spiel kann durch Anpassungen aber auch andere Phasen in den Fokus rücken (s.u.).
Welcher Kartentyp zuerst aufgedeckt wird, entscheidet außerdem über die Richtung des Darstellungswechsels, also welche Darstellungsform gesehen und interpretiert und welche sich zunächst gedanklich vorgestellt werden muss. Im folgenden Beispiel wird zunächst das Punktefeld interpretiert, dann die symbolische Darstellung gesucht.
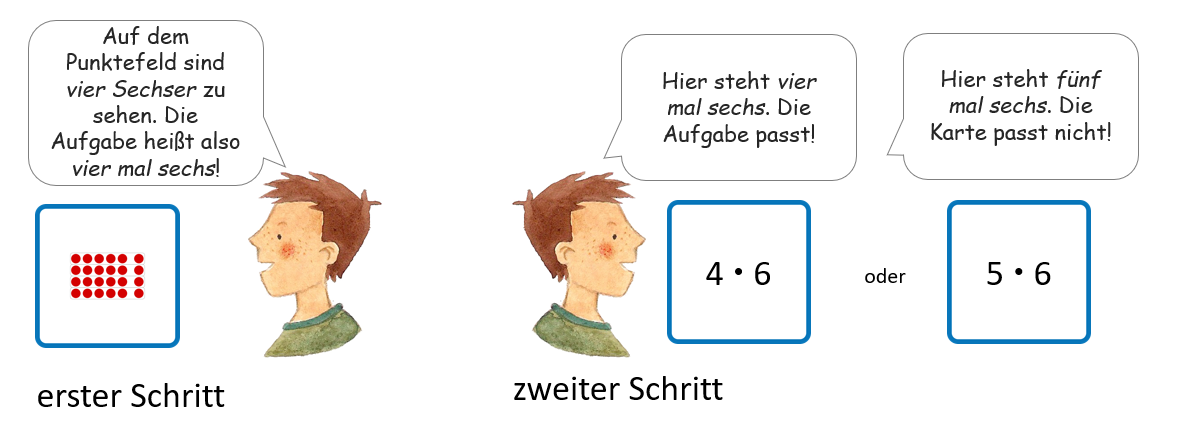
Es bietet sich an, das Spiel zu zweit zu spielen, wobei jeweils dem Spieler / der Spielerin, der/die nicht am Zug ist, die Rolle zukommt, auf Fehler zu achten und ggf. zu verbessern.
Material
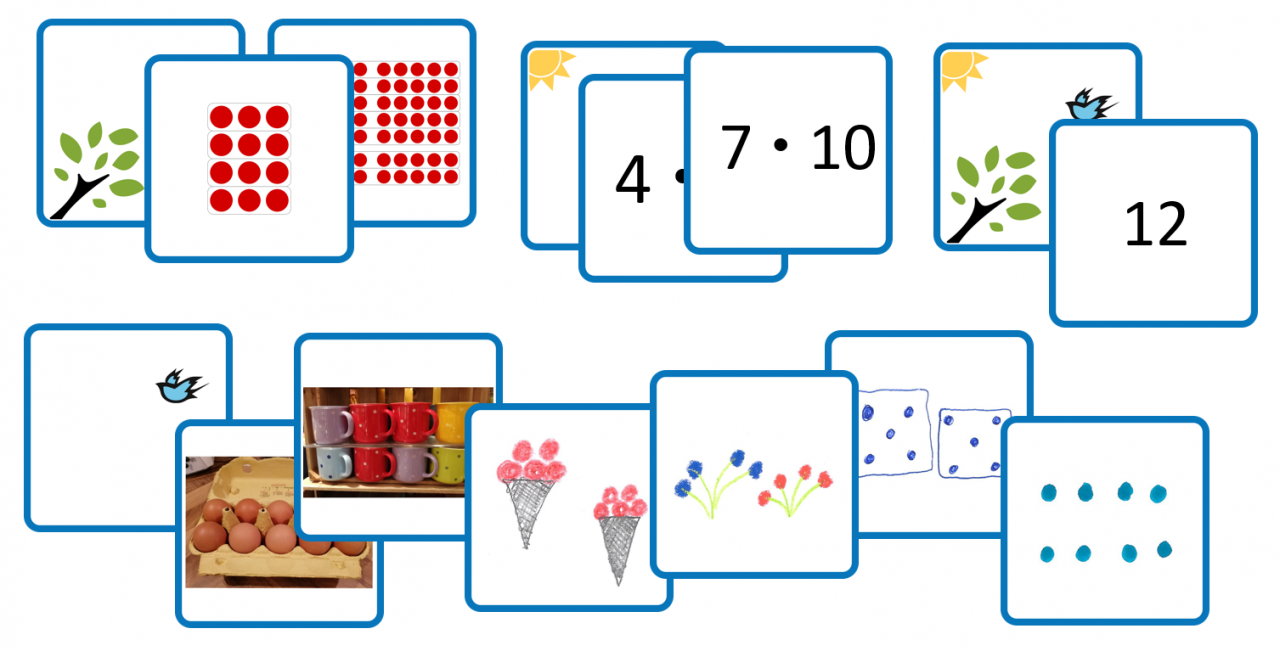
Im bereitgestellten Material ist die Punktefelddarstellung, die symbolische Darstellung der Aufgabe, sowie das Ergebnis vorhanden. Die Karten sind insgesamt vergleichsweise groß (sechs pro DIN A4) – dadurch sind auch größere Aufgaben noch gut als Punktefeld zu erkennen, außerdem sind die Karten haptisch einfacher zu handhaben. Für Kinder mit Schwierigkeiten in der Wahrnehmung ist außerdem ein reduziertes Set mit besonders großen Darstellungen und Aufgaben bis 55 vorhanden.
Damit die Karten beim Memoryspielen in zwei Gruppen, jeweils nach der Art der Darstellungsform ausgeteilt werden können, hat jede Darstellungsform eigene Motive auf der Rückseite.
Um das Sortieren und Auswählen von Aufgaben zu vereinfachen, ist das Mal-Memory in mehrere (auf der Vorderseite farblich kodierte) Sets gegliedert:
-
Set 0: besonders große Darstellungen, Aufgaben bis 55
-
Set 1: Reihen 1, 2, 5 und 10
-
Set 2: Reihen 3 und 4
-
Set 3: Reihen 6 und 9
-
Set 4: Reihen 7 und 8
Die Gliederung ist vor allem zur einfacheren Handhabung gedacht - das Memory sollte auch quer über alle Reihen hinweg gespielt werden.
Die Lernenden können außerdem eigene Darstellungen auf Blanko-Karten malen (wie beim Malquartett von PIK AS), oder Einmaleins-Fotos machen (fertige Einmaleins-Fotos gibt es außerdem bei PIK AS kompakt: Operationsverständnis Multiplikation). Dem eigenen Erstellen und Begründen von Darstellungen zu Malaufgaben kommt beim Aufbau des Operationsverständnisses große Bedeutung zu. Insbesondere, wenn Kinder mit der vorgegebenen Darstellung der Punktefelder noch Schwierigkeiten haben, macht es durchaus Sinn, sie einige Karten mit eigenen Darstellungen (oder Einmaleins-Fotos) herstellen und dann auch spielen zu lassen.
Der Punktefelddarstellung kommt als vorgegebene Repräsentation der Multiplikation besondere Bedeutung zu.
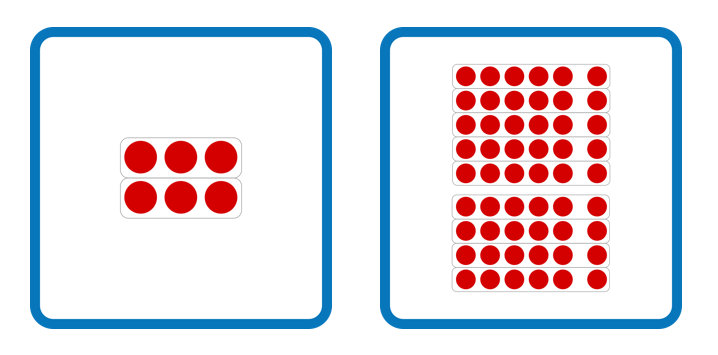
Die Anordnung der Punkte ist der Anordnung im 20er- bzw. 100er-Feld nachempfunden, mit der Herausstellung der „fünf“. Dadurch können die Lernenden einerseits an bereits erlernte Vorstellungen anknüpfen, andererseits eignet sich die Darstellung auch für die folgende Übungsphase, dem Vernetzenden Üben.
Die flächige Darstellung eignet sich für den Aufbau einer räumlich-simultanen Vorstellung der Multiplikation. Durch die visuell angedeutete Bündelung wird die Unterscheidung von Multiplikand und Multiplikator unterstützt, dies kann durch den Einsatz geeigneter Sprache noch verstärkt werden: Auf der ersten Karte sind „zwei Dreier(-Reihen)“ zu sehen, auf der zweiten „neun Sechser(-Reihen)“.
Es ist beim Spielen allerdings nicht entscheidend, dass die Kinder Multiplikand und Multiplikator, bzw. zwischen erster und zweiter Faktor immer gleich interpretieren und die entsprechenden Punktedarstellungen auswählen. Die Aufgabe „3 mal 4“ wird üblicherweise als drei horizontale Viererreihen dargestellt, kann sich jedoch durch Drehen um 90 Grad in die andere (eher unkonventionelle) Darstellungen überführen lassen (Aufgabe und Tauschaufgabe). Diese Erkenntnis bildet die Grundlage für die Entwicklung des Kommutativgesetzes. Wenn beim Spielen also Uneinigkeit entsteht, ob die Tauschaufgabe als Memory-Paar zugelassen werden soll oder nicht, kann dies als Anlass für einen gemeinsamen Austausch genommen werden. Dabei können einerseits die Vorteile von Konventionen („Ich kann genau festlegen, worüber ich spreche.“) thematisiert und diese in einem gemeinsamen Klassenwortspeicher (siehe unten) festgelegt werden. Andererseits kann die Bedeutung des Kommutativgesetzes etwa für das Automatisieren des Einmaleins diskutiert werden.
Sprache
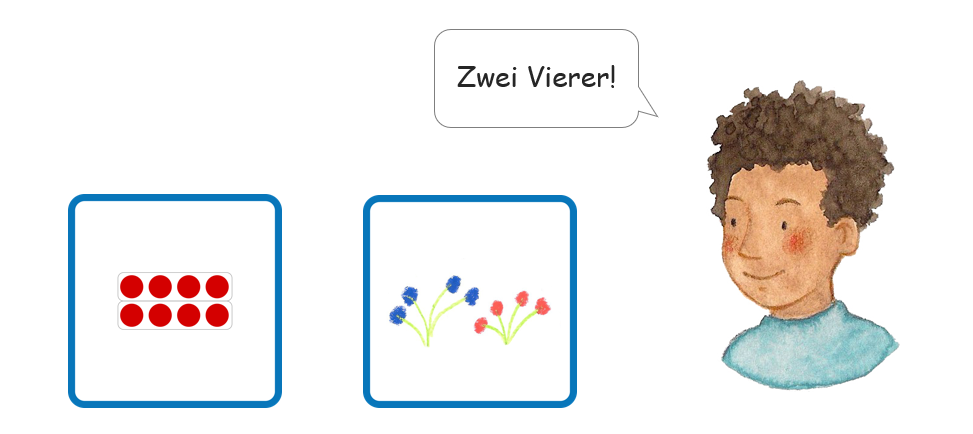
Wie bereits erläutert, kommt der sprachlichen Begleitung der Spielzüge besondere Bedeutung zu: Durch das Versprachlichen der umgedrehten Karten wird einerseits ein weiterer Darstellungswechsel vollzogen, andererseits können durch passende Sprachmittel bestimmte Vorstellungen angeregt werden. Die Formulierung des Satzbausteins „zwei Vierer“, ist ein ökonomisches und prägnantes Sprachmittel, das den Bündelungsaspekt der Multiplikation fokussiert (Prediger, 2019, 252), der wiederum auch visuell im Punktebild, aber auch in Schülerproduktionen erkennbar ist.
Damit Sprachmittel tragfähig werden, muss den Schülerinnen und Schülern die Gelegenheit gegeben werden, sich gemeinsam mit ihrem Begriffsinhalt auseinandersetzen können. Empfehlenswert ist hierfür ein Klassenwortspeicher, der gemeinsam geführt wird und in dem Begriffe festgehalten werden, deren Bedeutungsrahmen kollektiv abgeklopft, kontrastiert und assoziiert werden (Schütte, 2002).
Differenzierungsmöglichkeiten des Spielformats
Zahlenraum anpassen
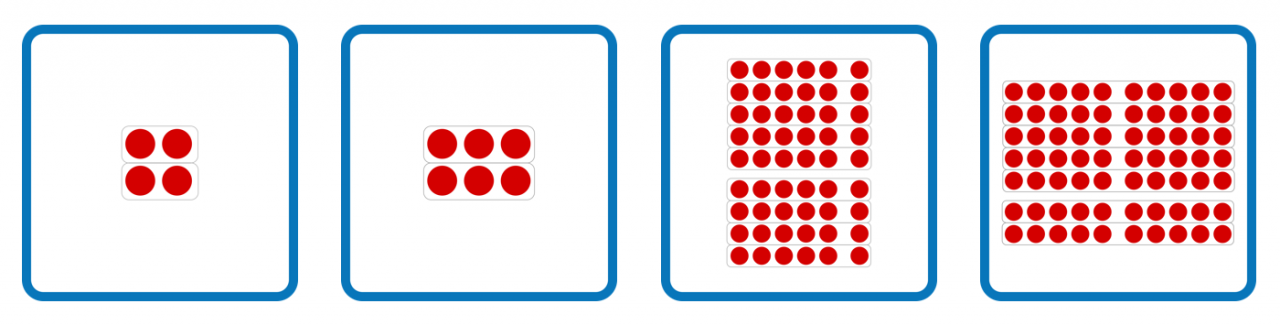
Beim Grundlegenden Üben sollten keine Hürden vorhanden sein, die den Aufbau von Verständnis erschweren. Die Lernenden müssen in der Lage sein, die Punktefelder schnell und ohne größere Anstrengung zu erfassen. Es kann also sinnvoll sein, für einige Lernende zunächst nur Aufgaben mit Faktoren bis „5“ spielen zu lassen. Diese Karten haben zusätzlich den Vorteil, dass die Punkte deutlich größer dargestellt sind. Schülerinnen und Schüler, denen die Zuordnung von kleinen Aufgaben schon allzu unbewusst gelingt, können auf der anderen Seite davon profitieren, mit größeren Faktoren umgehen zu müssen.
Zuordnen statt Umdrehen
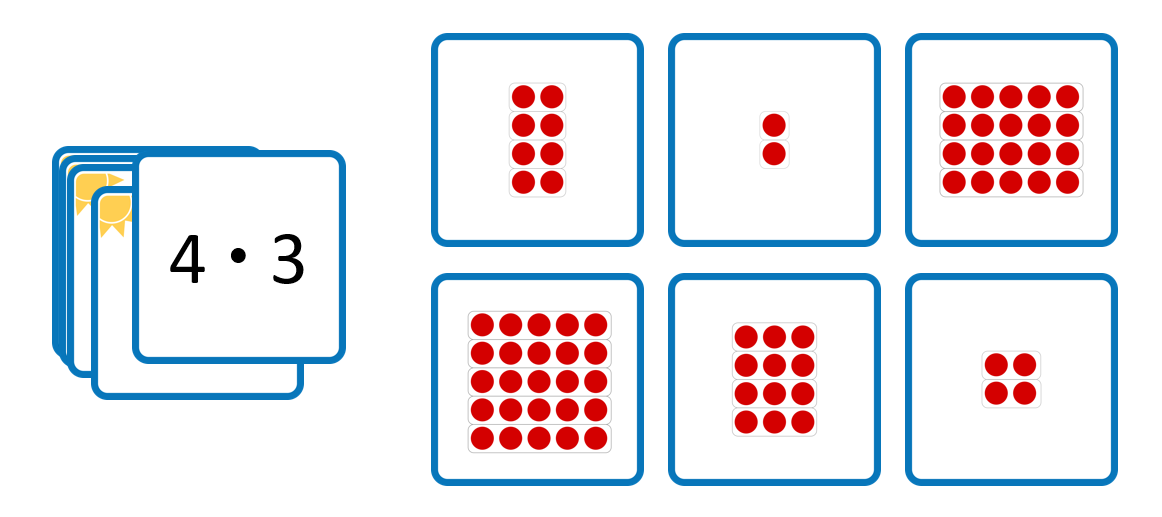
Dieser Modus ist vor allem empfehlenswert, wenn es Kindern noch schwerfällt, sich das passende Punktefeld zu einer symbolisch dargestellten Aufgabe gedanklich vorzustellen oder sie das Memory-Spiel emotional (häufig nicht-passende Paare aufdecken) oder kognitiv (sich den Ort einzelner Karten merken) überfordert. Sie haben hier die Möglichkeit mehrere Punktefelder miteinander zu vergleichen und auf ihre Passung zur Aufgabe zu überprüfen. Zum Ende des Spielzugs sollte dennoch eine Begründung eingefordert werden: „Diese Karte passt, weil insgesamt vier Dreier zu sehen sind.“
Legen und Überprüfen
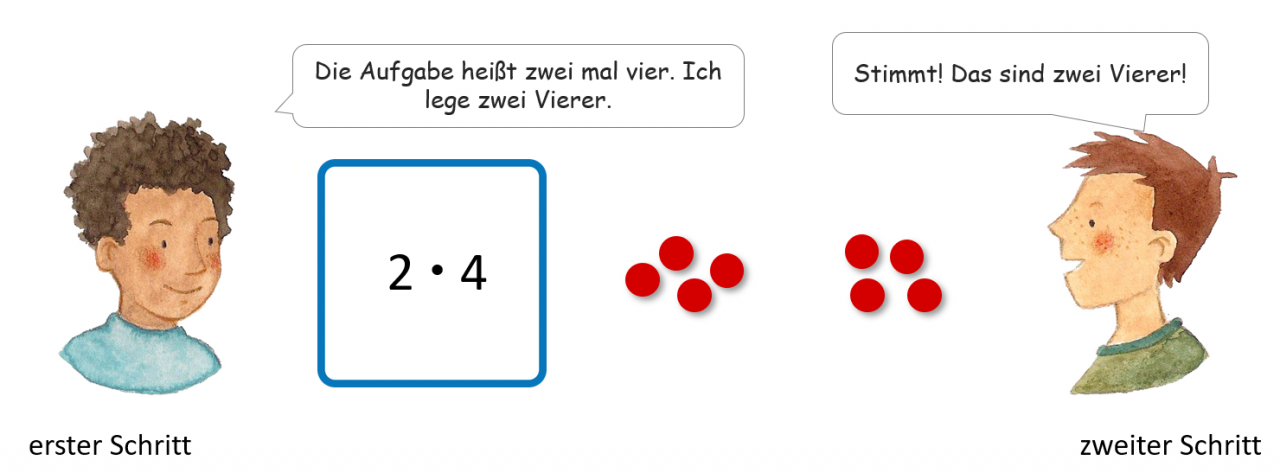
Durch die Handlung an konkretem Material wird die erste Phase des „Vier-Phasen-Modells“ (Wartha & Schulz, 2011, 11) in den Fokus dieses Spielmodus gerückt. Entscheidend ist auch hier wieder die sprachliche Begleitung des Spielzugs beider Partner. Zusätzlich kann auch thematisiert werden, wie man möglichst gut erkennen kann, ob es sich tatsächlich um die richtige Mal-Aufgabe handelt und somit ein Verständnis für die flächig-rechteckige Anordnung des Punktefeldes anbahnen.
Ergebnisse miteinbeziehen
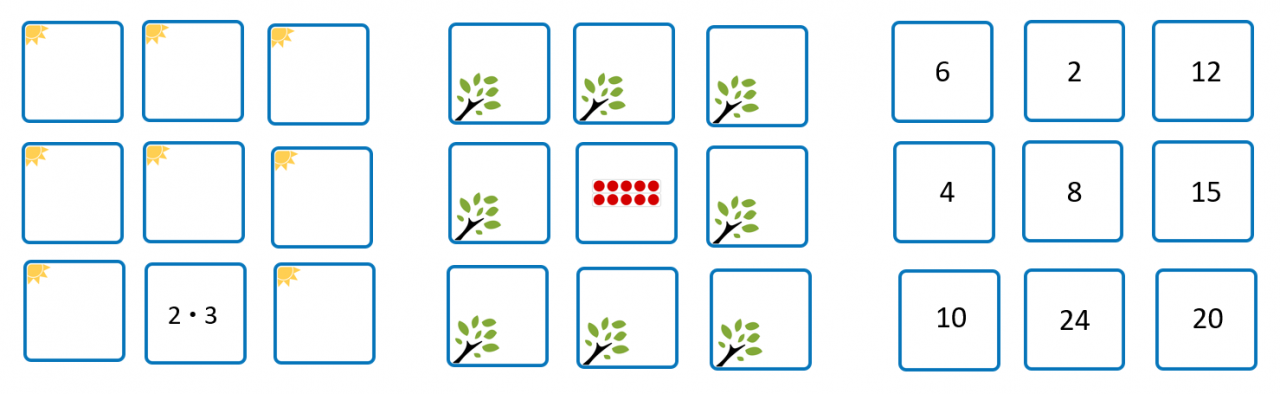
Eine weitere Differenzierung bietet die Möglichkeit, auch schon die Ergebnisse der Mal-Aufgaben mit einzubeziehen, bspw. kann immer dann, wenn ein Paar gefunden wird, zusätzlich das passende Ergebnis ausgewählt und genannt werden.