Schulleistungsmessung

 

Bei Verfahren zur Feststellung sonderpädagogischen Unterstützungsbedarfs stellt sich häufig die Frage, ob und in welchem Umfang sich bei einem Kind schulische Leistungsausfälle zeigen. In den Förderschwerpunkten Geistige Entwicklung und Lernen werden Eltern und Lehrkräfte fast immer durch Lernrückstände und Leistungsausfälle auf möglichen Unterstützungsbedarf aufmerksam, in anderen Förderschwerpunkten können auch außerschulische Auffälligkeiten auf Unterstützungsbedarf hindeuten. In allen Fällen kann eine unvoreingenommene Messung der aktuellen Schulleistungen helfen, die schulische Situation eines Kindes zu beurteilen. 

Im Förderschwerpunkt Lernen kommt den Lern- und Leistungsausfällen besondere Bedeutung zu. Hier gilt für alle Bundesländer, dass Unterstützungsbedarf nur dann festgestellt werden kann, wenn schulische Lernrückstände belegt sind. Für Nordrhein-Westfalen legt die Ausbildungsordnung sonderpädagogische Förderung (AO-SF 2019) in § 3 fest, dass „Lern- und Entwicklungsstörungen (Lernbehinderung, Sprachbehinderung, Erziehungsschwierigkeit)“ einen „Bedarf an sonderpädagogischer Unterstützung … begründen“ können und präzisiert in § 4 (2):

Ein Bedarf an sonderpädagogischer Unterstützung im Förderschwerpunkt Lernen besteht, wenn die Lern- und Leistungsausfälle schwerwiegender, umfänglicher und langdauernder Art sind.

Wie soll nun festgestellt werden, ob bei einem Kind Lern- und Leistungsausfälle vorliegen? Man könnte versuchen, typische Aufgaben aus dem aktuellen Unterricht im Lesen, Schreiben und Rechnen zu wählen und zu prüfen, ob und wie ein Kind diese löst. Ein solches Vorgehen hat den Vorteil, dass sich die Diagnostik direkt am aktuellen Unterricht orientiert (Curriculare Validität), aber das kann zu Fehlurteilen führen, wenn die Person, welche die Diagnostik durchführt 

• keine Aufgaben wählt, die repräsentativ für den Unterricht sind,
• die Lösung eines Kindes nicht richtig verstanden hat, 
• an die Lösungen zu hohe Maßstäbe anlegt. 

Die Beurteilung der Lösungen und der Lösungswege eines Kindes durch eine Einzelperson fallen subjektiv aus, denn sie sind von den professionellen Erfahrungen und individuellen Wertvorstellungen dieser Person geprägt. Die Zuschreibung sonderpädagogischen Unterstützungsbedarfs hat für ein Kind jedoch erhebliche bildungsbiografische Konsequenzen: In den Förderschwerpunkten Geistige Entwicklung und Lernen führt sie zu einer Beschulung gemäß einem zieldifferenten Bildungsgang mit reduzierten Leistungsanforderungen. Subjektive Fehlurteile sind möglichst zu vermeiden, deshalb verwendet man bei der Messung der Schulleistungen in der Regel wissenschaftlich erarbeitete und geprüft Testverfahren. 

Was sind Schulleistungstests?

Schulleistungstests sind standardisierte und normierte diagnostische Instrumente, die messmethodischen Standards genügen. Sie werden in der Regel schriftlich vorgegeben und verwenden Aufgaben, die nach curricularen Analysen als repräsentative Anforderungen ausgewählt wurden. Die Aufgabenformate sind geprüft worden, ebenso die Beobachtungs- und Bewertungskriterien. Auf diese Weise werden subjektive Entscheidungen durch Einzelpersonen bei der Testadministration und -auswertung weitgehend vermieden und durch objektive, für alle gleiche Vorgaben ersetzt. Die Interpretation der Ergebnisse, die ein Kind erzielt, orientiert sich ebenfalls nicht am individuellen Eindruck der Person, die den Test durchgeführt hat, sondern an differenzierten Vergleichsdaten, die in einer ausreichend großen und im Idealfall repräsentativen Eichstichprobe erhoben wurden und eine vergleichende Beurteilung nach statistischen Standards erlauben. 

In der Vergangenheit waren mehrdimensionale Schulleistungstests gebräuchlich, die Kenntnisse und Fertigkeiten in mehreren Schulfächern zu erfassen suchten. Inzwischen handelt es sich bei der Mehrzahl von Verfahren um Tests, die ein Schulfach oder einen bzw. mehrere Lernbereiche in einem Schulfach in den Blick nehmen (Hesse & Latzko, 2017, S. 207-209), nicht selten verbunden mit dem Anspruch, in mehreren Lernbereichen eines Faches Basiskompetenzen differenziert zu erfassen. 

Es gibt zwar einige wenige Schulleistungstests für sachunterrichtliche Fächer, aber die große Mehrzahl der Verfahren bezieht sich auf die Diagnose der Leistungen in den Kernfächern Deutsch und Mathematik. Im Folgenden soll exemplarisch ein Test einer Testreihe betrachtet werden, die im Lernbereich Mathematik mit Gewinn eingesetzt werden kann.

Der BASIS-MATH-G 3+ – ein exemplarischer Schulleistungstest Mathematik

Unter dem Titel BASIS MATH entwickelt Elisabeth Moser Opitz seit 2010 mit zahlreichen Kolleginnen und Kollegen eine Reihe von Testverfahren, mit denen überprüft werden kann, ob Lernende zentrale mathematische Kompetenzen der Grundschulmathematik – den so genannten mathematischen Basisstoff – erworben haben und sicher beherrschen. Die Tests gehen von der empirisch belegten Erkenntnis aus, dass rechenschwache Schülerinnen und Schüler zentrale Inhalte der Grundschulmathematik nicht oder nicht ausreichend verstanden haben und deshalb in ihrer Lernentwicklung beeinträchtigt sind. Sie sind so angelegt, dass sie im unteren Leistungsbereich besonders gut differenzieren (Moser Opitz, Ramseier & Reusser, 2013).

Der BASIS-MATH-G 3+ ist einer dieser Schulleistungstests (Moser Opitz, Stöckli, Grob, Reusser & Nührenbörger, 2019). Er kann als Einzel- oder Gruppentest durchgeführt und im vierten Quartal der 3. Klasse und im ersten Quartal der 4. Klasse eingesetzt werden. Damit die Testdurchführung in einer Kleingruppe oder im Klassenverband gelingen kann, muss sichergestellt werden, dass die Kinder die Aufgabenformate verstehen und wissen, wo und wie sie ihre Antworten notieren. Zu diesem Zweck werden zwei Beispielaufgaben mit dem Tageslichtschreiber vorgegeben und mit den Kindern besprochen. 

Die Einführung beginnt mit der Aufgabe „Lena kauft ein“ (Moser Opitz, Stöckli, Grob, Reusser & Nührenbörger, 2019, S. 38). „Da, wo es heißt ‚Schreibe auf, wie du rechnest‘, habt ihr Platz, um eure Rechnung aufzuschreiben,“ erklärt die Person, die den Test durchführt und fragt: „Was würdet ihr bei diesem Beispiel aufschreiben?“ 

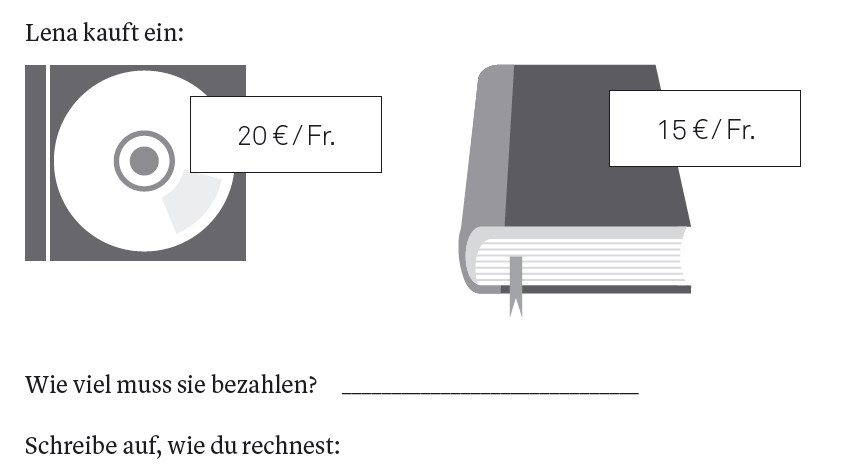
Beispielaufgabe "Lena kauft ein" aus der Einführung in den BASIS-MATH-G 3+ (aus Moser Opitz, Stöckli, Grob, Reusser & Nührenbörger, 2019, S. 38)

Die Kinder können die Aufgabe besprechen und gemeinsam lösen und sie werden angehalten, ihre Rechenwege aufzuschreiben und das Ergebnis einzutragen.

Die folgende Abbildung zeigt die zweite Einführungsaufgabe (Moser Opitz, Stöckli, Grob, Reusser & Nührenbörger, 2019, S. 39): „Hier seht ihr einen Zahlenstrahl (Strich entlangfahren). Den habt ihr bereits kennengelernt. Beim ersten Strich hier ist die Null (auf Strich zeigen). Beim letzten Strich ist die 1000 (auf Strich zeigen). Jede Zahl hat also einen bestimmten Platz. Wer weiß, welche Zahl beim zweiten Strich stehen müsste (auf Hunderterstrich zeigen)?“

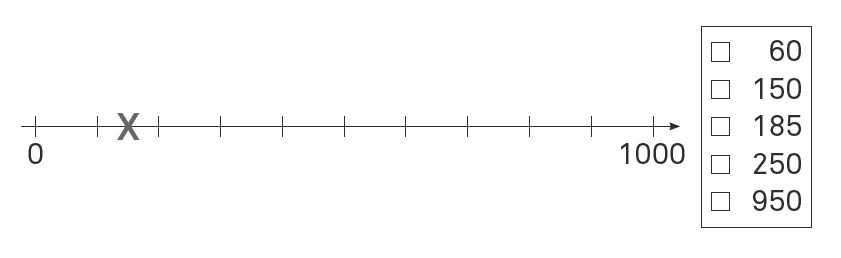
Beispielaufgabe "Zahlenstrahl" aus der Einführung in den BASIS-MATH-G 3+ (aus Moser Opitz, Stöckli, Grob, Reusser & Nührenbörger, 2019, S. 39)

Wenn im Gespräch deutlich wird, dass alle Kinder dem zweiten Strich die 100 zuordnen, wird das Aufgabenformat am Beispiel erklärt: „Wir müssen also herausfinden, welche Zahl hier, wo das Kreuz eingezeichnet ist (auf Kreuz zeigen), stehen müsste. Im Kasten (zeigen) habt ihr fünf Zahlen zur Auswahl. Gehört zu diesem Kreuz die Zahl 60, die Zahl 150, die Zahl 185, die Zahl 250 oder die Zahl 950?“ Es werden verschiedene Lösungsvorschläge besprochen und begründet, warum 150 die korrekte Lösung ist: „Genau, hier beim Kreuz ist die Zahl 150. Warum kann es nicht 185 sein?“ … „Richtig, das Kreuz ist genau in der Mitte zwischen dem Hunderterstrich und dem Zweihunderterstrich. 185 wäre näher bei 200 (mit Stiftspitze zeigen, wo die Zahl 185 ungefähr liegen würde). Wir kreuzen also das Kästchen für die Zahl 150 an (auf der Instruktionsvorlage ankreuzen). Beim Zahlenstrahl sollt ihr nichts hinschreiben. Ihr müsst nur die richtige Zahl ankreuzen.“

Die Auswahl der Testaufgaben orientiert sich am Curriculum des dritten Grundschuljahres und an empirischen Forschungen zu basalen Kompetenzen der Grundschulmathematik. Erfasst werden 

• das dezimale Stellenwertverständnis mit Aufgaben zur Zehnerbündelung und zum Entbündeln, zur Positionierung von Zahlen auf dem Zahlenstrahl und zum Multiplizieren mit Zehnerzahlen,
• das Operationsverständnis und die Grundvorstellungen von Multiplikation und Division mit Malrechnungen am Punktefeld und Aufgaben zum Zusammenhang von Multiplikation und Division,
• das Kopfrechnen durch Aufgaben zum Verdoppeln und Halbieren von zwei- und dreistelligen Zahlen, Subtraktionsaufgaben mit Zehnerübergang im Hunderterraum und relativ einfache Divisionsaufgaben, 
• Zahlergänzungsaufgaben auf glatte Zehner- oder Hunderterzahlen,
• das Zählen in Fünferschritten vorwärts und in Zehnerschritten rückwärts im Tausenderraum, 
• das mathematische Modellieren und Problemlösen bei Sachaufgaben und 
• halbschriftliche Rechenstrategien bei Additions- und Subtraktionsaufgaben mit Übertrag und mit großen Zahlen.

Wie wird der Test ausgewertet und interpretiert?

Nach Durchführung des Tests wird das Testheft eines Kindes gemäß den Angaben im Testmanual und mit Hilfe von Auswertungsvorlagen ausgewertet. Es werden die Rohwerte für alle Aufgaben und Inhaltsschwerpunkte ermittelt und anschließend wird im Testmanual in Normtabellen nachgeschlagen, wie sich die vom Kind erzielten Rohwerte im Vergleich zu den durchschnittlich erzielten Leistungen altersgleicher Kinder darstellen. Diese Normen beruhen im Falle des BASIS MATH 3+ auf einer in Deutschland, Österreich und der Schweiz erhobenen Stichprobe von gut 2.700 Kindern, die sich am Ende der 3. und am Anfang der 4. Klasse befanden.

Zur Beantwortung der Frage, ob bei einem Kind bedeutsame Lern- und Leistungsausfälle vorliegen, wird in der Regel der Gesamttestwert herangezogen, weil dieser auf vielen Aufgabenlösungen beruht und deshalb weitaus zuverlässiger misst als die Teilergebnisse in den Inhaltsbereichen, die nur auf relativ wenigen Aufgaben beruhen. Die klassische Methode der statistisch vergleichenden Beurteilung individueller Testwerte ist die Umrechnung eines erzielten Rohwertes in Prozentrangwerte, die man in den Testmanualen tabelliert vorfindet. Der Prozentrang gibt an, wie viele altersgleiche Kinder ein gleiches oder schwächeres Ergebnis erzielt haben.

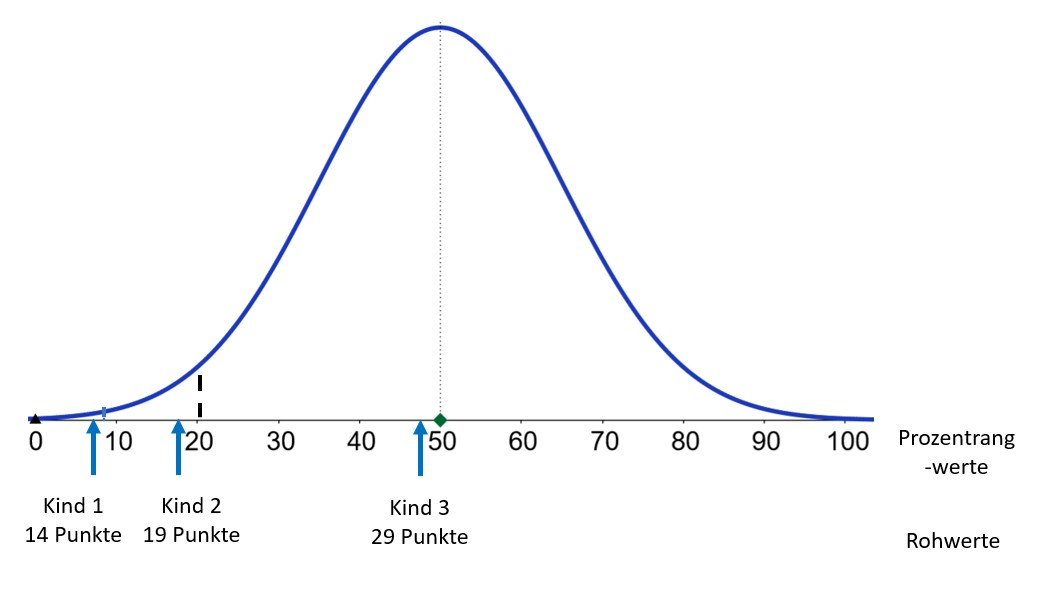
Drei Rohwerte und die diesen entsprechende Prozentrangwerte gemäß Normentabelle im Testmanual sowie die Grenzwerte für ausgesprochen schwache und recht schwache Leistungen (fiktive Werte, eigene Darstellung)
 

Das Vorgehen lässt sich an einem Beispiel nachvollziehen. Die Abbildung zeigt drei fiktive Rohwerte und deren Lokalisierung auf der Prozentrangskala. 

• Kind 1 hat 14 Punkte erzielt. Das entspricht laut Tabelle im Testmanual einem Prozentrang von 9 und bedeutet, dass etwa 9 Prozent der Kinder vergleichbaren Alters in der Eichstichprobe diese oder eine schwächere Punktzahl erreicht haben. Die von Kind 1 aktuell gezeigte Leistung liegt, wie in der Abbildung gezeigt, am unteren Ende der Verteilung. Sie entspricht einer ausgesprochen schwachen Leistung, denn alle Werte gleich oder unterhalb Prozentrang 9 lassen laut Testmanual auf erhebliche Rechenschwierigkeiten schließen.
• Kind 2 hat 19 Punkte erzielt. Das entspricht einem Prozentrang von 18. Die von Kind 2 aktuell gezeigte Leistung liegt, wie in der Abbildung gezeigt, noch im unteren Fünftel der Verteilung – sie entspricht laut Testmanual einer recht schwachen Leistung und sollte Anlass zu weiteren diagnostischen Abklärungen sein, da sich laut Manual bei Prozentrangwerten zwischen 10 und 19 Rechenschwierigkeiten nicht ausschließen lassen.
• Kind 3 hat mit 29 Punkten einen Prozentrang von 48 erzielt. Dieser Wert befindet sich deutlich über dem Grenzwert von 20 und somit im unkritischen Bereich, zumal er, wie in der Abbildung gezeigt, nahe am statistischen Durchschnitt liegt. Das Kind sollte recht gut mit den Anforderungen im Mathematikunterricht des dritten bzw. zu Beginn des vierten Schuljahres zurechtkommen.

Der Vergleich mit sorgfältig ermittelten Normen hilft bei der sachlichen Beschreibung und unvoreingenommenen Beurteilung der aktuellen schulischen Leistungen eines Kindes, unabhängig von den bisherigen Schulnoten und unabhängig vom Leistungsstand in der Schulklasse, die das Kind besucht (Schmidt-Atzert, Krumm & Amelang, 2021). Das Besondere an den Tests der BASIS MATH-Reihe ist, dass darüber hinaus zwei weitergehende, für Unterricht und individuelle Förderung besonders relevante Fragen verfolgt werden können:

• Auf der Ebene der einzelnen Aufgaben können die Rechenwege und Lösungsstrategien in verschiedenen mathematischen Inhaltsbereichen erfasst werden. Im Testmanual werden zu jeder Aufgabe Angaben zu deren statistischer Schwierigkeit gemacht und es werden die inhaltlichen Anforderungen einer jeden Aufgabe erläutert. Auf diese Weise lassen sich Hinweise für eine weiterführende Diagnostik sowie für spezifische Fördermaßnahmen gewinnen, um fehlende oder lückenhafte mathematische Verstehensgrundlagen aufzuarbeiten.
• Da es eine Serie von ähnlich aufgebauten Tests für mehrere Schuljahre gibt, die sich interpretativ über sog. Ankeraufgaben aufeinander beziehen lassen, können individuelle Lernfortschritte und Lernfortschritte einer Lerngruppe innerhalb eines Schuljahres und über die Schuljahre hinweg dokumentiert und kritisch geprüft werden, um im Falle von Schwierigkeiten frühzeitig und gezielt eingreifen zu können.

Was ist bei der praktischen Anwendung in der Schule zu beachten?

Für Schulleistungstests gilt, wie für alle Testverfahren: Die Diagnose kann nur gelingen, wenn in der schulischen Praxis aktuelle Testverfahren zur Verfügung stehen und wenn sie von den mit der Diagnostik betrauten Lehrpersonen fehlerfrei und kompetent angewendet werden. Huber (2000) oder Joél (2017, 2021) haben in empirischen Studien festgestellt, dass in der Praxis bei Testvorbereitung, Testdurchführung und Testauswertung erhebliche Mängel zu beklagen sind, welche die Validität von diagnostischen Urteilen gefährden. 

• Manchmal werden veraltete Testverfahren eingesetzt, weil nur diese verfügbar oder den Lehrpersonen bekannt sind. Die curriculare Validität eines Schulleistungstests ist jedoch nur dann gegeben, wenn dieser laut Manual gemäß den geltenden Lehrplänen entwickelt wurde, und seine statistische Validität ist davon abhängig, dass die Normen repräsentativ erhoben wurden und nicht veraltet sind. 
• Manchmal gefährden fehlende Testmaterialien, Protokollbögen oder Auswertungshilfen eine Testdurchführung und -auswertung gemäß Vorgaben. Nicht selten finden Testungen in schlecht ausgestatteten Räumen und unter Zeitdruck statt.
• Bei der Auswertung wird das Testalter nicht immer gemäß den Vorgaben berechnet, Rohpunkte werden falsch addiert und tabellierte Normwerte falsch abgelesen, statistische Kennwerte fehlerhaft gebildet oder nicht korrekt interpretiert.
• Häufig werden die vorgegebenen Instruktionen in dem Bemühen, ein Kind zu entlasten und es auch unter schwierigen Bedingungen testen zu können, nicht nur in zulässiger Weise variiert, sondern durch zusätzliche Erklärungen und informative Rückmeldungen ergänzt. 

Schulleistungstests müssen als standardisierte Tests den Vorgaben konform durchgeführt werden, soweit dies im individuellen Fall möglich ist, weil sonst der Vergleich der Leistungen eines einzelnen Kindes mit den Normdaten zu Fehlschlüssen führen kann. Bei Kindern mit Deutsch als Zweitsprache kann es nötig sein, dass die Aufgabenstellungen sprachlich erläutert werden. Bei manchen Kindern ist die zeitliche Abfolge von Testaufgaben zu ändern, sind Ruhepausen einzulegen, ist zusätzliche Zeit zu geben oder das Kind zum Weitermachen zu ermutigen. Solche Adaptionen dürfen jedoch keine Lösungshinweise beinhalten – beim BASIS MATH G 3+ ist z. B. nur eine verkürzte Wiederholung von Aufgabenerklärungen zulässig (Moser Opitz, Stöckli, Grob, Reusser & Nührenbörger, 2019, S. 40).

Adaptionen sollten grundsätzlich im Testprotokoll vermerkt und bei der Beurteilung der Ergebnisse berücksichtigt werden. Eine Offenlegung der Testbedingungen ist in gutachterlichen Stellungnahmen zur Feststellung von Unterstützungsbedarf unverzichtbar, damit die diagnostischen Entscheidungen nachvollzogen werden können und nicht der Eindruck entsteht, dass Unterstützungsbedarf voreilig zugesprochen wird. 

Was leisten Schulleistungstests bei der Feststellung von Unterstützungsbedarf?

Schulleistungstestergebnisse eignen sich zur Fundierung von Selektionsentscheidungen (Kuhl, Wittich & Schulze, 2022), denn sie ersetzen subjektive Vorgehensweisen durch objektive und standardisierte Verfahren und subjektive Beurteilungen durch den Vergleich mit statistischen Normen. Schulleistungstestergebnisse sind weniger geeignet, wenn es um individuelle pädagogische Entscheidungen im Hinblick auf Unterricht und Förderungen geht. Sie dürfen nicht pädagogisch überinterpretiert werden und die Testergebnisse sollten den Lernenden und ihren Eltern oder Erziehungsberechtigten mit pädagogischem Einfühlungsvermögen vermittelt werden (Schmidt-Atzert, Krumm & Amelang, 2021). 

• Schulleistungstests sind in der Regel produktorientiert, nicht prozessorientiert. Sie messen die aktuellen Schulleistungen im Idealfall objektiv, reliabel und valide, aber sie erfassen keine Lernstrategien und sie geben keine Hinweise auf mögliche pädagogische Hilfen.
• Schulleistungstests messen zwar die aktuellen Schulleistungen, aber sie erklären nicht deren Zustandekommen. Die Gründe für gute oder weniger gute Leistungen sind vielfältig und von Kind zu Kind verschieden. Sie können im Kind und seinen Anstrengungen, im familiären und soziokulturellen Umfeld und in der Lebenssituation des Kindes, in seiner schulischen Situation, in der Beziehung zu den Lehrpersonen oder in den Beziehungen zu den anderen Schülerinnen und Schülern zu finden sein.
• Schulleistungstests messen zwar die aktuellen Schulleistungen und sie erlauben vorsichtige Prognosen über zukünftige Leistungsentwicklungen, aber wer heute wenig Erfolg in der Schule hat, muss nicht dauerhaft erfolglos sein. Wenn es z.B. gelingt, die familiäre und die schulische Situation eines Kindes zu verbessern und ihm guten Unterricht zu bieten, können sich auch seine schulischen Leistungen verbessern.

Einige Schulleistungstests wie der hier vorgestellte BASIS MATH 3+ erlauben, in Leistungsprofilen die individuellen Stärken und Schwächen eines Kindes in einzelnen Untertests abzubilden. Solche Profile basieren zwar auf relativ wenigen Aufgaben und sind deshalb wegen geringer Reliabilität mit Vorsicht zu interpretieren, aber sie können, wie gezeigt, wichtige Anhaltspunkte für mögliche nächste Schritte im Unterricht oder in der individuellen Förderung geben. Die Tests der BASIS MATH-Reihe stellen in dieser Hinsicht und mit ihrer dezidierten Orientierung auf eine möglichst gute Differenzierung der Leistungen im unteren Leistungsbereich eine Ausnahme dar.

---

Interessieren Sie sich für andere Schulleistungstests in Mathematik oder in anderen Schulfächern? Bei Tully (2014, S. 284-286) und Lauth, Grünke & Brunstein (2014, S. 560-571) und auf der Webseite der Testzentrale finden Sie Übersichten und weitere Informationen.

---