Mögliche Schwierigkeiten
Mögliche Schwierigkeit: Unzureichendes Verständnis der Begriffe Teil, Anteil, Ganzes und ihrem Zusammenhang
Die Begriffe Teil, Anteil und Ganzes müssen verständig genutzt werden können. Die Lernenden müssen verstehen, dass Anteile immer in Bezug zu seinem Ganzem und einem Teil interpretiert werden müssen. Hierbei kommt es auf die Relation des Teils zum Ganzen an: Die Begriffe und ihre Zusammenhänge müssen systematisch und operativ erarbeitet und verinnerlicht werden. Besonders der Begriff Anteil ist für viele Lernende zunächst schwierig (Prediger et al., 2017, S. 21). Um die Erarbeitung dieser Begriffe handlungsorientiert zu ermöglichen, kommt dem Papier als Anschauungsmittel eine besondere Bedeutung zu. Durch das Falten von Anteilen mit Papier erfahren die Lernenden, dass der Anteil umso kleiner wird, je größer der Nenner ist. Sie können zudem systematisch untersuchen, wie sich eine Veränderung des Nenners bei gleichbleibendem Zähler und Ganzen auf den Teil und den Anteil auswirkt.
Mögliche Schwierigkeit: Das Ganze wird nicht in gleich große Teile zerlegt
Die Teile eines Ganzen müssen gleich groß sein, nur dann ist die Zerlegung mathematisch korrekt (Padberg & Wartha 2017, S. 25). Einige Lernende beachten die Größe der Stücke nicht. Sie teilen ein Ganzes zwar entsprechend der Zahl im Nenner, zeichnen die Teile aber unterschiedlich groß ein (Schink, 2013, S. 35).
Abbildung 1: Mögliche Aufgabenstellung
Abbildung 2: Zwei fehlerhafte Lösungen (links) und eine korrekte Lösung (rechts)
Mögliche Schwierigkeit: Einseitige Fixierung auf kardinale Zahlvorstellungen aus dem Bereich der natürlichen Zahlen
Die Lernenden müssen die Zahlaspekte der natürlichen Zahlen umdenken bzw. ihre Grundvorstellungen erweitern (Unterschiede zwischen den natürlichen Zahlen und Bruchzahl). Aktivieren Lernende eine kardinale Zahlvorstellung aus dem Bereich der natürlichen Zahlen und nicht die Vorstellung vom Bruch als Anteil, so kann es vorkommen, dass sie den Nenner als Größenangabe interpretieren. Daraus können verschiedene falsche Interpretationen von Brüchen resultieren. Ausgewählte Fehlvorstellungen werden im Folgenden dargestellt.
Es kann sein, dass ein Bruch als zwei separate natürliche Zahlen interpretiert wird, nicht aber als Ausdruck einer Relation zwischen einem Teil und einem Ganzen (Schink, 2013, S. 35).
Abbildung 3: Mögliche Aufgabenstellung
Abbildung 4: Fehlerbeispiel zur Darstellung des Bruchs \({1 \over 4}\)
Dieses Lösungsbeispiel zeigt eine mögliche Interpretation der Zahlen des Bruchs \({1 \over 4}\) als natürliche Zahlen. Entsprechend wurden vier Teile markiert, nicht aber \({1 \over 4}\) des Ganzen.
Aktivieren Lernende ihre kardinale Zahlvorstellung aus dem Bereich der natürlichen Zahlen, so kann dies ein Grund sein, warum sie noch nicht verstehen: Ein Stammbruch (Bruch mit dem Zähler 1) mit einem kleineren Nenner hat einen größeren Wert als ein Stammbruch mit einem größeren Nenner (Schmassmann & Moser Opitz, 2011, S. 72).
Abbildung 5:
Missverständnisse beim Vergleich von Bruchzahlen
Im Umgang mit Stammbrüchen gilt also: ein Stammbruch mit einem kleineren Nenner hat einen größeren Wert als ein Stammbruch mit einem größeren Nenner. Dies kann im Umgang mit gemischten Brüchen bei Lernenden zur fälschlichen Annahme führen, dass der Bruch mit dem kleineren Nenner immer den größeren Wert hat. Beim Vergleichen von Brüchen kommt es aber immer auf den Zähler und den Nenner an.
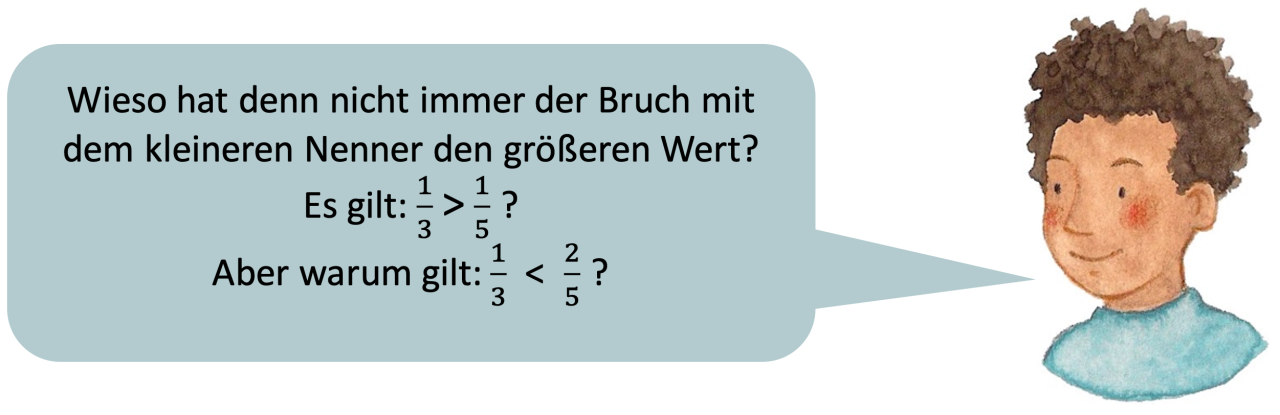Abbildung 6:
Missverständnisse beim Vergleich von Bruchzahlen
Mögliche Schwierigkeit: Empirisches statt strukturelles Bruchverständnis
Bruchteile mit gleichem Namen können ungleich groß sein. Eine Hälfte eines kleinen Apfels ist kleiner als die Hälfte eines großen Apfels (Schmassmann & Moser Opitz, 2001, S. 72). Die Lernenden müssen sich bei Brüchen - wie auch schon bei den natürlichen Zahlen – von der Wahrnehmung einzelner Objekte lösen.
Abbildung 7: Bezug zwischen Bruch und Ganzem
Abbildung 8: Mögliche Aufgabenstellung
Abbildung 9: Korrekte Lösungen
Die Abb.9 zeigt vier verschiedene korrekte Lösungen zur oben aufgeführten Aufgabe: Markiere immer genau \({1 \over 4}\) deines gefalteten Papiers. Das Beispiel zeigt, dass der Bruch \({1 \over 4}\) das Verhältnis eines Bruchteils zu einem Ganzen beschreibt, ganz unabhängig von der wahrnehmbaren Gestalt des jeweiligen Ganzen.
Mögliche Schwierigkeit: Den Anteil in Beziehung zum Ganzen setzen
Das Ganze kann unterschiedlich groß sein und unterschiedliche Formen haben (z. B. ein Rechteck, ein Kreis, eine Tafel Schokolade). Insbesondere bei bildlichen Darstellungen kann es für Lernende eine besondere Herausforderung darstellen, den Anteil mit dem Ganzen in Verbindung zu bringen (Schink 2013, S. 343).
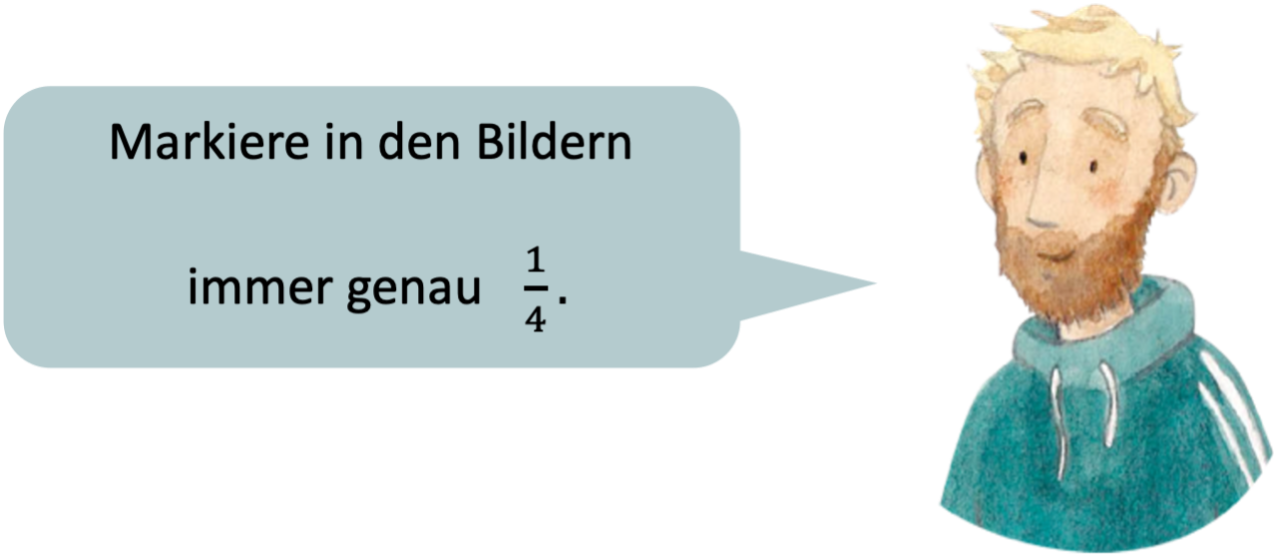Abbildung 10: Mögliche Aufgabenstellung
Abbildung 11: Exemplarische Bilddarstellungen
Oft fällt es Lernenden besonders schwer, ein in Teile strukturiertes Ganzes zu interpretieren, wenn die Anzahl der Teile größer ist als die Zahl im Nenner des Anteils, wie es z.B. auch oben bei der Pizza der Fall ist.
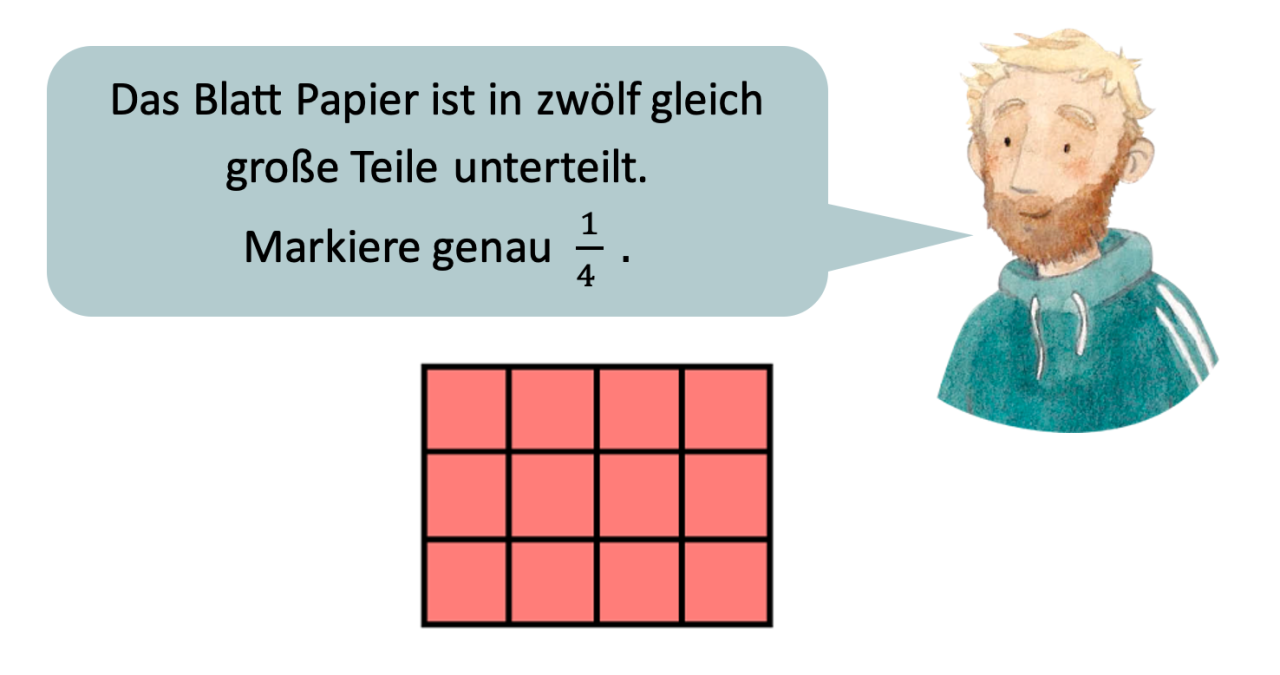Abbildung 12: Mögliche Aufgabenstellung
Abbildung 13: Beispiel für eine fehlerhafte Lösung
Bei dieser Lösung wurde der Anteil nur auf einen Teil des Ganzen angewendet. \({1 \over 4}\) von zwölf Teilen wurde auf \({1 \over 4}\) von vier Teilen (eines in zwölf Teile geteilten Ganzen) reduziert (Schink, 2013, S. 342). In diesem Beispiel hat das Kind die erste Zeile vermutlich als Ganzes gedeutet und den Anteil auf die Zeile bezogen markiert.
Mögliche Schwierigkeit: Erschließung des Ganzen
Aufgaben, in denen das Ganze nicht gegeben ist, sondern erschlossen werden muss, stellen für Lernende ebenfalls oft eine besondere Hürde dar (Schink, 2013, S. 47). Aufgaben, bei denen dabei mit dem Kreismodell gearbeitet wird, wie im folgenden Beispiel, sind dabei oft wenig herausfordernd, da der Kreis bzw. Kuchen leicht zu einem Ganzen vervollständigt werden kann.
Abbildung 14:
Erschließung des Ganzen am Kreismodell
Aus diesem Grund eignet sich das Kreismodell für Aufgaben zur Erschließung des Ganzen nicht besonders gut – im Gegenteil: Die kognitive Herausforderung, die nötig ist, um von einem gegebenen Teil auf ein Ganzes zu schließen, wird den Lernenden hier durch das Modell abgenommen, ein echter Lernzuwachs kann nicht erfolgen. Daher eignen sich für dieses Lernziel eher Rechteckdarstellungen.
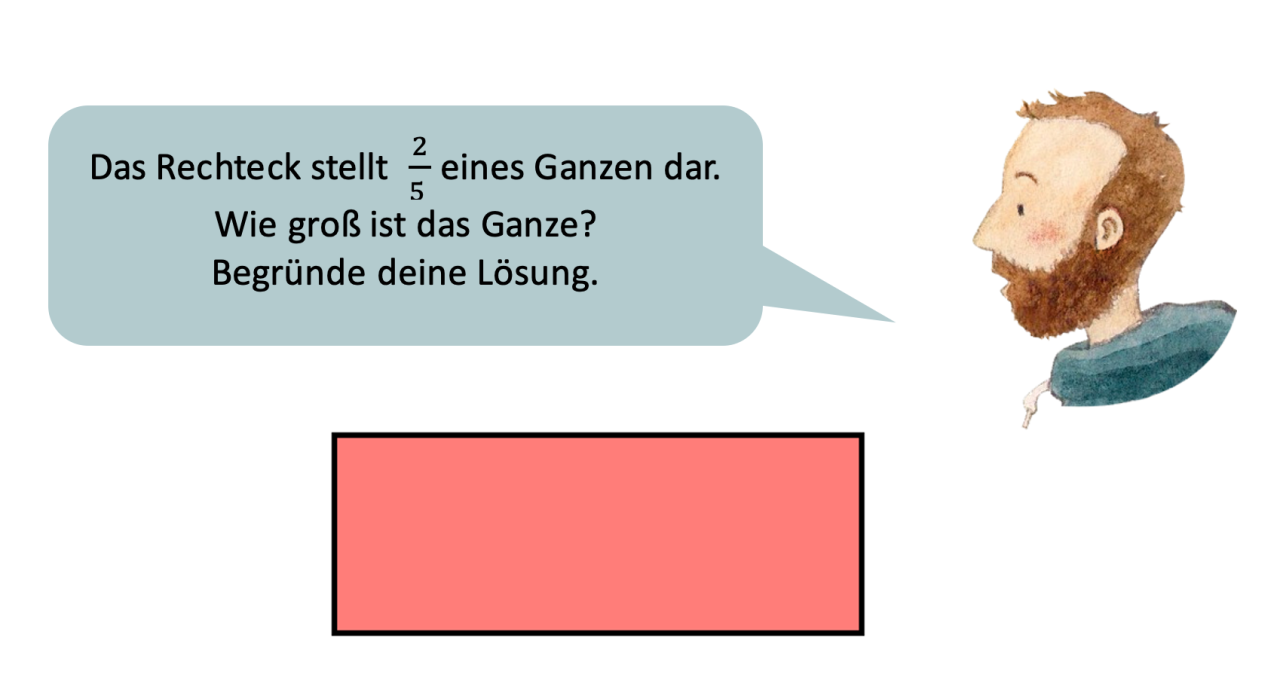Abbildung 15: Erschließung des Ganzen am Rechteckmodell
