Bruchvorstellungen
Kinder machen in ihrem Alltag erste intuitive Begegnungen mit Teilen und Anteilen, etwa beim Teilen von Kuchen oder beim Abmessen von Zutaten. Auch im Mathematikunterricht der Grundschule sammeln sie Erfahrungen, z. B. mit ersten gebräuchlichen Bruchzahlen bei Größenangaben und lernen, diese in andere Einheiten umzuwandeln (MSB NRW, 2021, S. 92).
Diese Erfahrungen führen aber noch nicht zu stabilen Bruchvorstellungen. Denn auch wenn viele Lernenden alltagsgebräuchliche Bruchzahlen (z.B. Stammbrüche) korrekt lesen können, bedeutet dies nicht, dass sie zu Beginn der 6. Klasse inhaltliches Verständnis über Bruchzahlen besitzen und beispielsweise Zusammenhänge zwischen Bruchzahlen und bildlichen Darstellungen herstellen können (Padberg & Wartha, 2017, S. 36).
Eine fachlich fundierte Thematisierung von Brüchen ist deshalb notwendig. Bevor auf einer formal-regelhaften Ebene gearbeitet wird, ist der ausreichend intuitiver und anschaulicher Vorstellungen zu Brüchen von zentraler Bedeutung (Malle, 2004, S. 4).
Ein Verständnis der Bruchzahlen wird aufgebaut, indem Grundvorstellungen zu Brüchen aktiviert werden und Übersetzungen zwischen unterschiedlichen Darstellungsebenen vorgenommen werden (Padberg & Wartha, 2017, S. 1-3). Die folgende Abbildung zeigt vielfältige mögliche Darstellungsvernetzungen zwischen den Ebenen Sprache, Mathesprache/ Symbole, Bilder und Handlungen.
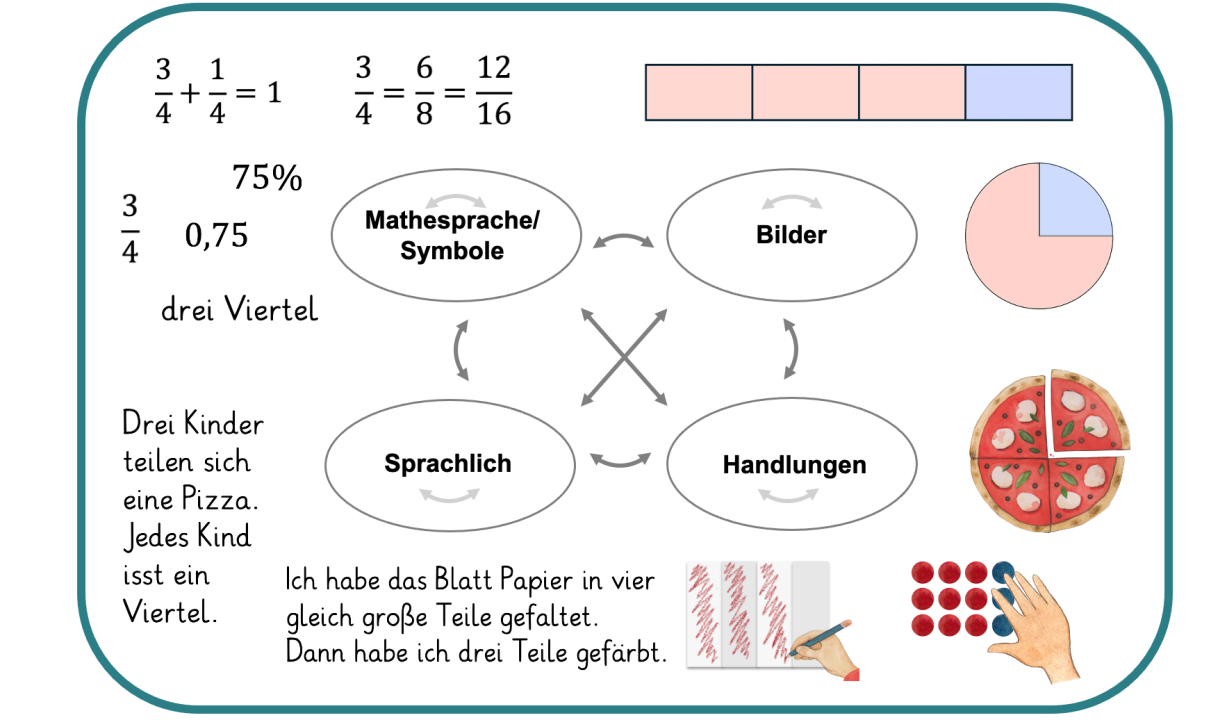Abbildung 1: Darstellungsvernetzungen
Das zentrale Ziel der vorliegenden Aufgabenstellungen kompakt ist, den Lernenden Aktivitäten zur Entwicklung der zentralen Grundvorstellung Bruch als Anteil bereitzustellen, damit sie auf diese Weise tragfähige Bruchvorstellungen und ein Verständnis der Bruchzahlen aufbauen können.
Unterschiede zwischen den natürlichen Zahlen und Bruchzahlen
Mit der Einführung der Bruchzahlen wird der bisher für die Lernenden vertraute Zahlbereich der natürlichen Zahlen erweitert. Werden die Zahlaspekte der natürlichen Zahlen mit denen der Bruchzahlen verglichen, so wird schnell deutlich, wo für die Lernenden besondere Hürden entstehen können, welche Vorstellungen verändert bzw. erweitert werden müssen und welche neu dazukommen (Padberg & Wartha, 2017, S. 151-153). Auf einige Besonderheiten wird im Folgenden näher eingegangen.
Zahlaspekte: Im Vergleich der Zahlaspekte der natürlichen Zahlen und der Bruchzahlen fällt auf, dass nur die Zahlaspekte Maßzahl und Rechenzahl in ihrer Bedeutung für die Bruchzahlen unverändert bestehen bleiben, der Operatoraspekt wird stark modifiziert, andere Zahlaspekte verschwinden völlig oder bleiben in spezieller Form erhalten (ebd., S. 38). Deutlich wird dies an den nachfolgenden zwei Beispielen:
-
Kardinalzahlaspekt: Während eine natürliche Zahl die Mächtigkeit einer Menge angibt (Wie viele?), zählen Bruchzahlen keine Elemente, sondern beschreiben einen Anteil einer Menge (Wie viele Teile vom Ganzen?).
-
Ordinalzahlaspekt: Ordnungszahlen beschreiben im Bereich der natürlichen Zahlen eine Position/Reihenfolge, einen Rangplatz. „Juri ist die 2. Person in der Warteschlange.“ Auch Bruchzahlen können in einer Reihenfolge stehen. Während allerdings bei den natürlichen Zahlen jede Zahl genau einen Vorgänger und einen Nachfolger hat (vor Juri steht die 1. Person in der Reihe, hinter ihm die 3. Person), gibt es zwischen zwei Bruchzahlen unendlich viele weitere Bruchzahlen – auch in einer scheinbar gut abzählbaren Reihe \({1 \over 4}\), \({2 \over 4}\), \({3 \over 4}\), \({4 \over 4}\) ist \({1 \over 4}\) nicht der direkte Vorgänger von \({2 \over 4}\).
Abbildung 2: Zahlenstrahl
Darüber hinaus lernen die Schülerinnen und Schüler mit den Bruchzahlen einige neue Zahlaspekte kennen: Anteil, Verhältnis, Quotient, Lösung linearer Gleichungen (ebd., S. 39). Vor allem der für die Lernenden neue Zahlaspekt Bruch als Anteil hat für das Verständnis von Brüchen eine grundlegende Bedeutung. Dieser Zahlaspekt beschreibt eine zentrale Grundvorstellung für das Verständnis von Brüchen und wird weiter unten ausführlicher dargestellt.
Schreibweisen: Die natürlichen Zahlen verfügen über eine eindeutige Schreibweise, während die Bruchzahlen viele verschiedene Schreibweisen besitzen: gemeiner Bruch (z. B.\({1 \over 3}\) bzw. ein Drittel), Dezimalbruch (z. B. 0,4), Maßstab (z. B. 1 : 30.000), Verhältnis (z. B. 6 zu 9 oder 6 : 9), Quotient (3 : 4), Prozent (z. B. 30%), Promille (z. B. 3%) (ebd., S. 32). Diese Vielfalt an Schreibweisen ebenso wie die Kombination von Zahlen mit Operationszeichen kann Lernende vor besondere Schwierigkeiten stellen. Ähnlich wie beim Positionsprinzips des dezimalen Stellenwertsystems (https://pikas-mi.dzlm.de/node/529) bestimmt auch beim Bruch die Position der Zahl, welche Bedeutung sie für den Wert des Bruchs hat:
Die Position oder die Stelle einer Ziffer innerhalb einer natürlichen Zahl gibt Aufschluss über den Wert dieser Ziffer: Die Ziffer 2 hat in den Zahlen 2, 527 oder 3209 jeweils einen anderen Wert, einmal sind es zwei Einer, im zweiten Beispiel zwei Zehner und im dritten Beispiel sind es zwei Hunderter (vgl. Krauthausen & Scherer, 2007, S. 18).
Bei einer Bruchzahl ist das ähnlich: Je nachdem ob die 2 über dem Bruchstrich (also bei \({2 \over 7}\) oder unter dem Bruchstrich (also bei \({7 \over 2}\) im Nenner) steht, bedeutet sie etwas anderes: Eine Zahl im Zähler gibt an, wie viele Teile gemeint sind, eine Zahl im Nenner, in wie viele gleich große Teile das Ganze geteilt wurde.
Hinzu kommt die Tatsache, dass jeder Bruch zwar eindeutig auf dem Zahlenstrahl verortet ist, aber diese mit beliebig vielen verschiedenen gleichwerten Bruchzahlen bezeichnet werden kann (\({1 \over 3}\) = \({2 \over 6}\) = \({57 \over 171}\)).
Tragfähige Darstellungen
Bruchzahlen können auf verschiedene Arten dargestellt werden. Mit Hilfe von Gegenständen und Situationen aus dem Alltag, z. B. Verteilungssituationen, können Brüche repräsentiert und in Form von Rechengeschichten umgesetzt werden.
Im Mathematikunterricht werden in erster Linie geometrische Figuren/Bilder als Repräsentanten von Brüchen eingesetzt, vor allem Rechtecke/Quadrate, Strecken, Kreise und Quader/Würfel. Eine besondere Bedeutung kommt der Rechteckform zu, da die Unterteilungen in einem Rechteck leicht und auf verschiedene Arten von den Lernenden selbst hergestellt werden können und das Modell nicht nur im weiteren Verlauf der Bruchrechnung einsetzbar, sondern auch gut mental repräsentierbar ist (Padberg & Wartha, 2017, S. 32). In den vorliegenden Aufgabenstellungen kompakt (https://pikas-mi.dzlm.de/node/836) ist rechteckiges Papier deshalb das zentrale Arbeitsmittel für die Lernenden.
Abbildung 3: Beispiele von Lernenden zur Bruchzahldarstellung mit Papierrechtecken
Ein weiteres bedeutsames Anschauungsmittel für die Erarbeitung von Bruchvorstellungen ist der Bruchstreifen bzw. die Bruchstreifentafel. Mit Hilfe des Bruchstreifens können Anteile von Mengen sowie die Gleichwertigkeit von Brüchen anschaulich bestimmt werden. Einsatzmöglichkeiten zur Arbeit mit dem Bruchstreifen finden sich unter: (https://mathe-sicher-koennen.dzlm.de/node/336 (Prediger et al., 2014; vgl. auch Prediger, 2011; Wessel, 2015).
