Flexible Operationsvorstellungen
Der Aufbau von Operationsvorstellungen gilt als einer der zentralen Schwerpunkte im Mathematikunterricht der Primarstufe.
Kinder sollen lernen, zwischen verschiedenen Darstellungsformen von Operationen zu wechseln, Grundsituationen und Rechenaufgaben einander zuzuordnen oder Rechengesetze zu nutzen und zu beschreiben (vgl. MSW NRW, 2008).
Doch warum ist es so bedeutsam, dass Kinder Operationen „verstehen“ und Zusammenhänge zwischen den verschiedenen Rechenoperationen herstellen und nutzen können?
Die vier grundlegenden Rechenoperationen Addition, Subtraktion, Multiplikation und Division werden bereits im Anfangsunterricht der Grundschule thematisiert.
Wie wichtig flexible Operationsvorstellungen sind, wird vor allem dann deutlich, wenn sich die Kinder ab Klasse 3 in größeren Zahlenräumen bewegen: Fehlen diese, wird das (Weiter-) lernen im Fach Mathematik wesentlich erschwert (vgl. Häsel-Weide & Nührenbörger, 2013).
So zeigte sich in verschiedenen Untersuchungen, dass Schülerinnen und Schüler der weiterführenden Schulen, die auf grundlegende Inhalte der Grundschulmathematik (wie z. B. ein Verständnis für Operationen; vgl. Kasten 1) nicht zurückgreifen konnten, weitreichende Schwierigkeiten bei der Bearbeitung von Aufgabenstellungen und Inhalten der Sekundarstufe I hatten (vgl. Moser Opitz, 2007).
Wichtig ist deshalb, dass die konkrete Arbeit im Mathematikunterricht immer an den Verstehensgrundlagen ansetzt, denn „nachhaltiges Lernen muss sich gerade für die schwächeren Lernenden konsequent am Aufbau von Verständnis orientieren [...]“ (Prediger et al., 2014, S. 7).
Aufbau eines Verständnisses für Operationen – auch bei Kindern mit Lernschwierigkeiten?
Alle Schülerinnen und Schüler der Grundschule sollen Operationen verstehen lernen – in kleineren Zahlenräumen und auch in größeren. Für viele Kinder wird dies ein wesentliches Ziel in der Grundschule sein, an dem in der Sekundarstufe mit Bezug auf weitere Zahlbereiche angeknüpft wird.
Manche Kinder werden aber noch in der Sekundarstufe ihr Verständnis zu Operationen mit natürlichen Zahlen weiter ausbauen.
Konkret geht es daher im inklusiven Mathematikunterricht der Grundschule wie auch der Sekundarstufe darum, Vorstellungen über Operationen und deren Beziehungen zueinander auf- und auszubauen.
Darüber hinaus ist es bedeutsam, dass die Lernenden sichere Fertigkeiten beim Operieren mit Zahlen entwickeln – wie z.B. das sichere Zerlegen von kleinen Anzahlen, das Wissen um einfache Aufgaben und deren Bedeutung für das Ermitteln von Ergebnissen bei schwierigeren Aufgaben. Damit verknüpft sind immer auch Vorstellungen über Zahlen und Einsichten in Zahlbeziehungen (vgl. Moser Opitz, 2007; Prediger et al., 2013).
Die Entwicklung eines umfassenden Operationsverständnisses ist für alle Kinder (insbesondere auch für Kinder mit Lernschwierigkeiten!) eine wesentliche Voraussetzung für ein erfolgreiches (Weiter-)lernen im Fach Mathematik (vgl. Prediger et al., 2013).
Aber wodurch zeichnet sich ein umfassend ausgebildetes Verständnis für Operationen konkret aus?
Hier sind drei Merkmale kennzeichnend, die im Folgenden ausführlich erläutert werden:
-
Das Verfügen über flexible Operationsvorstellungen (Grundvorstellungen)
-
Die Fähigkeit zum Darstellungswechsel
-
Das Erkennen und Nutzen von Beziehungen und Strukturen zwischen Aufgaben untereinander (einfache und schwierige Aufgaben) und zwischen den verschiedenen Rechenoperationen
Flexible und somit tragfähige Operationsvorstellungen zeichnen sich dadurch aus, dass mathematische Operationen auf verschiedene Weise gedeutet und mit unterschiedlichsten Handlungssituationen oder strukturierten Abbildungen verknüpft werden können (vgl. Prediger, 2009). Doch was bedeutet das konkret? Und was heißt in diesem Zusammenhang verschieden?
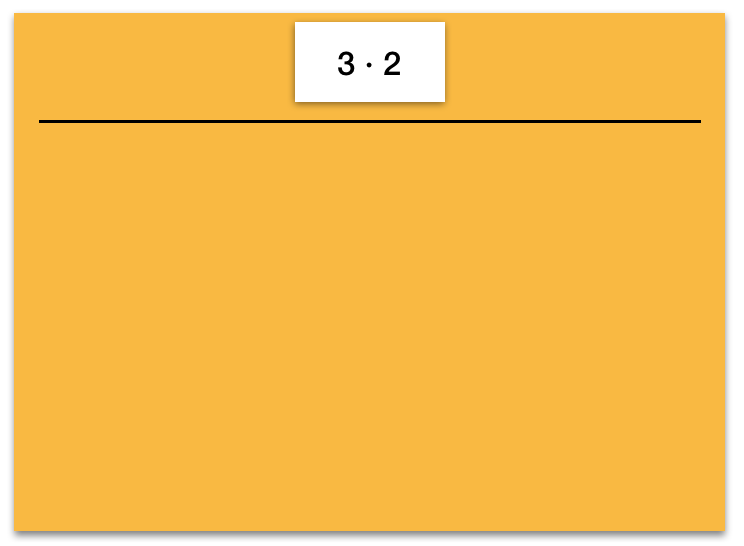Abbildung 1
Hierzu ein Beispiel:
Hatice und Paula erhalten eine Sortiertafel und Darstellungen von verschiedenen Multiplikationsaufgaben, die zudem unterschiedliche Grundsituationen der Multiplikation repräsentieren.
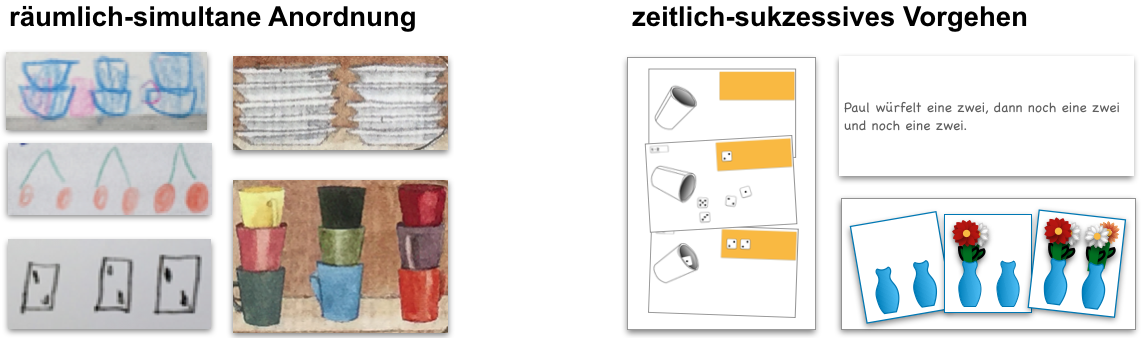Abbildung 2
Paula und Hatice sortieren die verschiedenen Darstellungen. Beide Schülerinnen legen jeweils die Darstellungen, die ihrer Ansicht nach zu der Multiplikationsaufgabe 3 · 2 passen, auf ihre Sortiertafel.
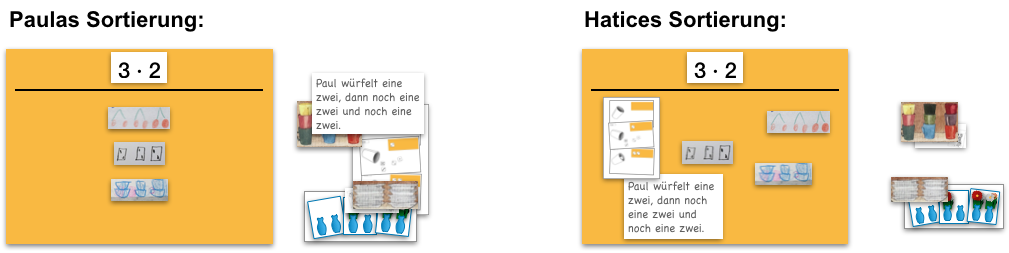Abbildung 3
Betrachtet man die Sortierung von Hatice, dann wird schnell deutlich, dass sie mit der Multiplikation verschiedene Grundsituationen, d.h. sowohl räumlich-simultane Anordnungen als auch ein zeitlich sukzessives Vorgehen verbindet.
Demgegenüber liegt den von Paula ausgewählten Darstellungen – obwohl auch diese „unterschiedlich“ sind (z. B. in Bezug auf die jeweilige Anordnung der Objekte) – allen die gleiche Grundsituation zur Multiplikation (Multiplikation als räumlich-simultane Anordnung) zu Grunde.
Paulas Vorstellungen zur Multiplikation scheinen somit eher einseitig ausgeprägt zu sein, obwohl sie „unterschiedliche“ Darstellungen auswählt.
Von flexiblen bzw. tragfähigen Operationsvorstellungen wird hingegen genau dann gesprochen, wenn bei der Deutung von Rechenoperationen oder der Interpretation von Handlungen oder Abbildungen verschiedene Grundvorstellungen aktiviert werden können (vgl. Hatices Sortierung).
Darstellungswechsel
Das Verfügen über Grundvorstellungen ist eng verknüpft mit der Fähigkeit zum Darstellungswechsel, denn erst „Grundvorstellungen zu Rechenoperationen ermöglichen Übersetzungen zwischen Darstellungsebenen“ (Wartha & Schulz, 2011, S. 6).
Gelingt es beispielsweise einem Kind, zwischen verschiedenen Darstellungen einer Rechenoperation (denen verschiedenen Grundsituationen zu Grunde liegen) flexibel zu wechseln bzw. Darstellungen in andere Darstellungen zu übersetzen, dann kann davon ausgegangen werden, dass es in Bezug auf diese Rechenoperation auf unterschiedliche Grundvorstellungen zurückgreifen kann (vgl. Kuhnke, 2013).
Darstellungsformen von Rechenoperationen
Zu den konkreteren Darstellungsformen von Operationen gehören Handlungen mit Materialien, Rechengeschichten oder Bilder. Zu den eher abstrakten Darstellungsformen zählen Darstellung mittels gesprochener oder geschriebener Symbole (vgl. Schulz & Schülke, 2017; Kuhnke, 2013).
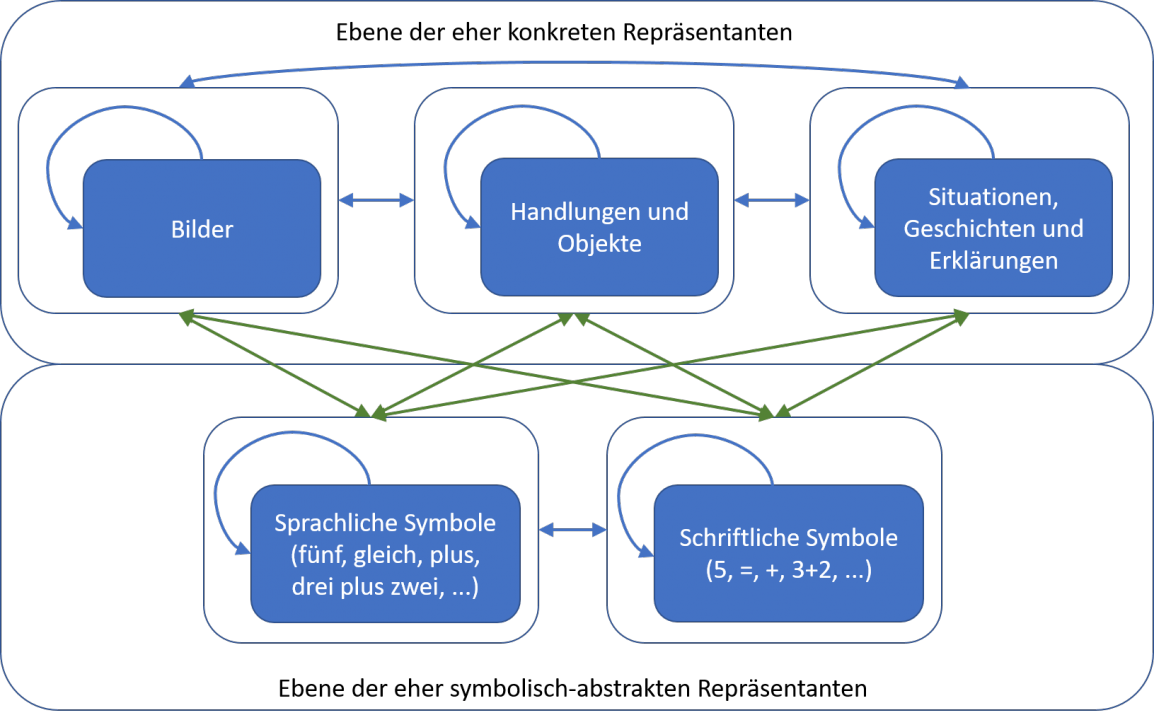Abbildung 7: Modell Darstellungswechsel (Schulz, 2020, S. 19)
Zu beachten ist hierbei, dass Übersetzungen nicht nur von einer Darstellungsform in eine andere erfolgen können (z.B. indem zu einer Rechengeschichte ein Rechenterm notiert wird), sondern auch innerhalb einer Darstellungsform, d.h. beispielsweise von einer bildlichen Darstellung in eine andere bildliche Darstellung.
Bilder und bildliche Darstellungen
Graphische Darstellung von Rechenoperationen (z.B. mittels eines Fotos oder einer Zeichnung).
Beispiele für bildliche Darstellungen zu dem Rechenterm 3· 3:
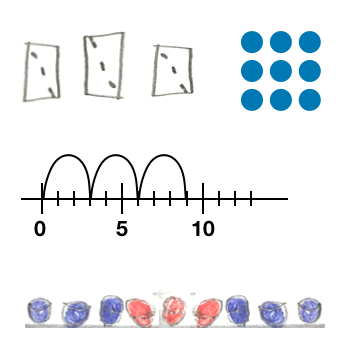Abbildung 8
Handlungen mit Material
Darstellung von Rechenoperationen mit Materialien (z.B. Wendeplättchen, Stifte, Bonbons, Klötze ...).
Aufteilen - 24 Stifte, immer 6 in ein Bündel.
Abbildung 9
Rechengeschichten und mündliche Erklärungen / Erläuterungen
Erzählerische Darstellung (z.B. im Rahmen einer Geschichte, die mathematisch interpretiert werden kann).
Audiodatei - in Vorbereitung
Verbal-symbolische Darstellungen
Darstellung mittels Verbalisierung der Rechensymbole und Zahldarstellungen. Unterschieden werden können mündliche und schriftliche Verbalisierungen.
Beispiel für schriftliche Verbalisierungen von Rechensymbolen und Zahldarstellungen:
"Ich habe erst die zwei Fünfen genommen, dann habe ich die letzte Fünf, dann wusste ich, dass es fünfzehn ist."
Abbildung 10A
Beispiel für eine „gemischte“ Verwendung von verbal-symbolischen und schriftlich-symbolischen Darstellungen:
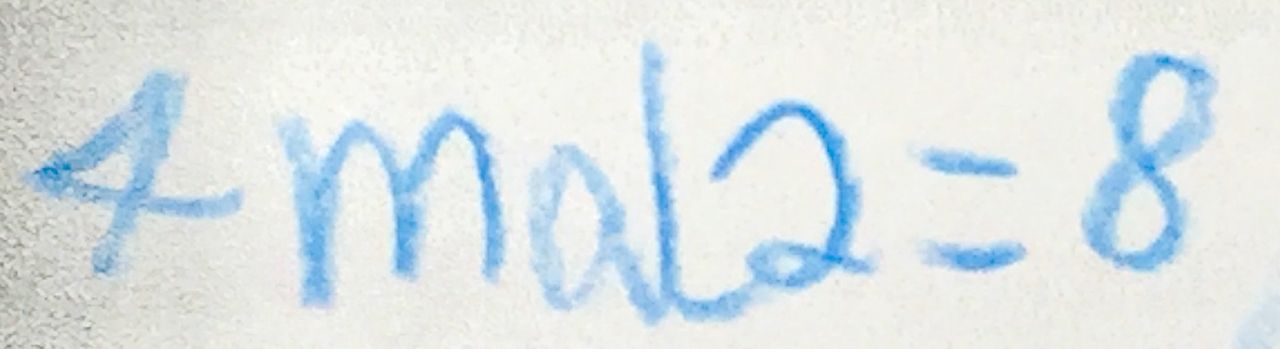Abbildung 10B
Schriftlich-symbolische Darstellungen
Beispiele für die symbolische Notation von Addition und Multiplikation:
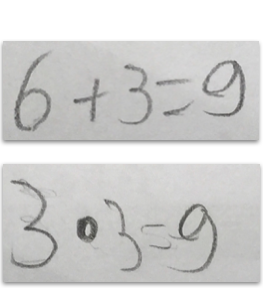Abbildung 11
Operationseigenschaften und Rechengesetze
In Vorbereitung
Folgerungen für den Unterricht
Tragfähige Zahlvorstellungen aufbauen
Damit Kinder verschiedene und flexible Operationsvorstellungen entwickeln und über den Zahlenraum bis 20 hinaus erfolgreich im Mathematikunterricht mitarbeiten können, ist es bedeutsam, dass sie über ihre Zählfähigkeiten und ein ordinales Zahlverständnis hinaus ein Verständnis von Kardinalität entwickeln und Zahlvorstellungen aufbauen, die anschluss- und tragfähig sind.
Ausführliche Hintergrundinformationen und Unterrichtsideen zum Aufbau von tragfähigen Zahlvorstellungen finden Sie unter Inhalte: Zahlvorstellungen.
Zentrale (Grund-)vorstellungen erarbeiten
Wichtig ist, in Bezug auf die einzelnen Rechenoperationen immer wieder Darstellungen verschiedener Grundsituationen anzubieten und den Kindern die Gelegenheit zu geben, sich mit diesen handelnd und gedanklich auseinanderzusetzen. Unverzichtbar ist hier das Gespräch mit anderen Kindern:
-
Gemeinsames Nachdenken: Das Ermöglichen von Handlungserfahrungen allein ist nicht ausreichend – vielmehr muss der Umgang mit Material eingebettet sein in einen Unterricht, in dem immer wieder auch das Versprachlichen und das gemeinsame Nachdenken über die konkreten Handlungen angeregt wird. Erst im Austausch kann es gelingen, strukturelle Gemeinsamkeiten und das Verbindende in unterschiedlichen Darstellungen zu erfassen und Grundvorstellungen aufzubauen (vgl. Fetzer & Söbbeke, 2019): „Du sagst, das Bild passt zu der Aufgabe. Erklär mal!" „Warum meinst du, dass das zueinander passt? Das verstehe ich nicht!“ (vgl. hierzu auch den Abschnitt: „mentale Operationsvorstellungen aufbauen“).
-
Handlungsideen anbieten: Bei der Erarbeitung von Grund- bzw. Operationsvorstellungen mit Material kann es sinnvoll sein, Kindern mit Lernschwierigkeiten Handlungsideen anzubieten und ein mögliches Vorgehen zu zeigen. Wichtig ist in diesem Zusammenhang, dass die Handlungsidee ein Angebot darstellt und keine verpflichtende Vorgabe (vgl. Häsel-Weide, 2016).
-
Rückbezüge herstellen: Auch wenn die Operationsvorstellungen gesichert scheinen: Es ist sinnvoll, regelmäßig Übungen zum Darstellen von Rechenoperationen mittels Material oder anhand von Bildern und zum Übersetzen zwischen Darstellungen durchzuführen. Hierbei sollten den Kindern immer wieder Hilfen angeboten werden, die das Übersetzen zwischen und Darstellen von Rechenoperationen unterstützen (z.B. sprachliche Vorgaben und Beispiele, fokussierende Ausschnitte ...).
-
Besonders sorgfältig bei Einführung der Multiplikation und Division arbeiten: Schwierigkeiten ergeben sich insbesondere beim Aufbau von Operationsvorstellungen zu den Rechenoperationen Multiplikation und Division. Hier muss besonders sorgfältig vorgegangen werden (vgl. Prediger et al., 2013).
Mentale Operationsvorstellungen aufbauen
Auf der Grundlage des Handelns mit Materialien, des Zeichnens von Bildern und des gemeinsamen Nachdenkens über konkrete Rechenoperationen gilt es dann, mentale Vorstellungen (Grundvorstellungen) aufzubauen. Zentral ist hierbei, dass es den Kindern gelingt, Rechenoperationen bzw. operative Beziehungen in den Handlungen und Zeichnungen gedanklich zu sehen:
"Die Grundidee beim Aufbau von Grundvorstellungen ist, dass konkrete Handlungen an geeigneten Materialien zu gedanklichen Operationen umgebaut werden" (Wartha & Schulz 2011, S. 11; H. i. O.).
Kinder benötigen bei diesem Prozess der Verinnerlichung von Handlungen dann Unterstützung, wenn sie beispielsweise eine Rechenoperation ohne den Einsatz von Materialien nicht durchführen können oder ihnen die Versprachlichung ihrer konkreten Handlungen nicht gelingt.
Das Vierphasenmodell zeigt hier eine Möglichkeit auf, Kinder bei dem Prozess der Ausbildung mentaler Operationsvorstellungen zu unterstützen (vgl. hierzu auch Aebli, 1980; vom Hofe, 1995).
Abbildung 12: Vierphasenmodell (Wartha & Schulz 2012, S. 63)
Angemerkt werden muss an dieser Stelle, dass das Modell nicht im Sinne einer Stufenfolge aufgefasst werden darf – so gibt es sicher viele Schülerinnen und Schüler, die ohne zusätzliche Unterstützung mentale Operationsvorstellungen entwickeln und sozusagen direkt von Phase 1 in Phase 4 wechseln. Ebenso gewinnen alle vier Phasen in unterschiedlichen Zahlenräumen oder bei der Arbeit mit verschiedenen Materialien (z.B. Rechenoperationen am Dienes-Material oder mit Hilfe von Plättchen und Punktefeldern) immer wieder neu an Bedeutung.
Das Vierphasenmodell – eine Möglichkeit zur Unterstützung von Kindern mit Lernschwierigkeiten
Während vielen leistungsstärkeren Kindern der Prozess der Verinnerlichung von Handlungen oft „automatisch“ gelingt, benötigen insbesondere Schüler und Schülerinnen mit Lernschwierigkeiten hierbei Unterstützung. Das Vierphasenmodell „wurde als Leitfaden für die Organisation von Lernumgebungen und zur Dokumentation von Lernfortschritten bei der Förderung besonders leistungsschwacher Kinder und Jugendlicher entwickelt“ (Wartha & Schulz, 2011, S. 13).
Vor der Arbeit mit dem Vierphasenmodell sollte zunächst eine genaue Diagnostik erfolgen:
-
In welcher der Phasen arbeitet das Kind bereits sicher – in welcher Phase werden Schwierigkeiten sichtbar?
Zugleich müssen bei der Arbeit mit lernschwächeren Kindern (!) weitere Aspekte beachtet werden:
-
Die 2. bzw. 3. Phase sollte nicht übersprungen werden
-
Treten in einer Phase Schwierigkeiten auf, sollte die vorangegangene Phase wieder aufgegriffen werden (d.h. nicht sofort wieder auf das Handeln mit Material zurückgreifen).
-
Ändert sich der Kontext oder der mathematische Inhalt der Handlungen, die verinnerlicht werden sollen, muss wieder in Phase 1 angesetzt werden.
Achten Sie zudem darauf, dass das Kind nicht die Beschreibungen „automatisiert“ und auswendig gelernt aufsagt, sondern die Handlungen bedeutungsvoll erläutern kann.
Weiterführende Informationen und zwei Videosequenzen, in denen die Arbeit nach dem Vierphasenmodell zu sehen ist, finden Sie in der Rubrik Leitideen in der zweiten Hälfte des Moduls Diagnose-/ und Fördergespräche: Unterricht.
Unterschiedliche Darstellungen vernetzen
Die Fähigkeit, zwischen verschiedenen Darstellungen einer Rechenoperation wechseln und eine Darstellung in eine andere übersetzen zu können, stellt einen Indikator für flexible Operationsvorstellungen dar (vgl. hierzu Abschnitt: „Merkmale bzw. Indikatoren flexibler Operationsvorstellungen“).
Zugleich kann die Entwicklung von Operationsvorstellungen durch die Anforderung, zwischen und innerhalb verschiedenen Darstellungsformen zu übersetzen, gefördert werden (vgl. Schulz & Schülke, 2017; Kuhnke, 2013 ).
Das bedeutet, dass im Mathematikunterricht der Fokus immer wieder auch auf Übersetzungsaktivitäten gelegt werden muss.
Wichtig ist dabei, alle Darstellungsformen in den Blick zu nehmen und Darstellungswechsel auch begründen zu lassen („Warum passt das zueinander?“) (vgl. Häsel-Weide, 2016).
Hinweise zur Diagnose
Um Informationen über die Operationsvorstellungen eines Kindes zu erlangen, können in einem Gespräch mit dem Kind verschiedene Darstellungswechsel angeregt werden.
Dabei muss beachtet werden, dass die Wechsel zwischen den verschiedenen Darstellungsformen unterschiedliche Anforderungen an die Kinder stellen.
So zeigen sich beispielsweise in einer Untersuchung von Sprenger (2008, S. 711) die größten Schwierigkeiten „bei Aufgaben, die eine inhaltliche Deutung mathematischer Ausdrücke verlangten (vom Symbol weg, hin zu Bild oder Handlung)“.
Auch die Übersetzung von Text- bzw. Sachaufgaben in eine Rechnung ist oft komplex und verlangt neben flexiblen Operationsvorstellungen noch andere Kompetenzen (so muss beispielsweise der Sinngehalt sprachlich verstanden werden).
Mögliche Anregungen für Darstellungswechsel:
Eine Möglichkeit herauszufinden, ob bzw. welche Vorstellungen Kinder mit bestimmten Rechenoperationen verknüpfen, besteht beispielsweise darin, zu einer konkreten Aufgabe eine Zeichnung erstellen zu lassen.
„Stell dir vor, du erklärst einem anderen Kind die Aufgabe 3 + 4. Wie würdest du das machen?“
Eine weitere Möglichkeit besteht darin, eine Zeichnung und verschiedene Rechenaufgaben vorzugeben. Die Kinder werden aufgefordert, die Aufgaben zu markieren, die ihrer Ansicht nach zu der Zeichnung passen und ihre Zuordnungen zu begründen.
Insbesondere die Arbeit mit Sortiertafeln stellt eine gute Möglichkeit dar, den Fokus der Kinder auf die Vernetzung von Darstellungen zu richten und die Kinder herauszufordern, passende Darstellungen einander zuzuordnen:
„Welche Darstellungen passen zusammen?“ „Begründe deine Sortierung.“
Im kleineren Zahlenraum arbeiten: Liegt der Fokus im Unterricht auf dem Darstellungswechsel, bietet es sich an, in einem Zahlenraum zu arbeiten, im dem sich die Kinder sicher bewegen (z.B. im Zahlenraum des vorangegangenen Schuljahres).
Hierdurch können insbesondere Kinder mit Lernschwierigkeiten entlastet werden. Zugleich verschiebt sich der Fokus weg von der Ergebnisermittlung hin zu den verschiedenen Darstellungsformen und zur Vernetzung von Darstellungen.
Das Arbeiten in kleineren Zahlenräumen (beispielsweise im Zahlenraum bis 20) bietet den weiteren Vorteil, dass Zeichnungen und Handlungen einfacher und in der Regel übersichtlicher gestaltet werden können.
