Das folgende Praxisbeispiel zeigt beispielhafte Ausschnitte aus Diagnose- und Fördergesprächen mit einer Schülerin der zweiten Jahrgangsstufe.
Diagnosegespräche
Vorbereitung des Diagnosegesprächs: Standortbestimmung und Leitfaden
Die Diagnosegespräche orientierten sich an einer vorangegangen Standortbestimmung (vgl. ‚Diagnose- und Förderaufgaben‘; s. auch PIKAS: Haus 9: Lernstände wahrnehmen – Unterrichtsmaterial – Standortbestimmungen), welche Aufgaben zu Zahl- und Operationsvorstellungen im Zahlenraum bis 100 behandelt.
Auffällig waren bei Zara neben Zahlendrehern beim Notieren der Aufgabenstellungen auch Unregelmäßigkeiten beim Durchführen von Operationen (s. Abb. 2 und Abb. 3).
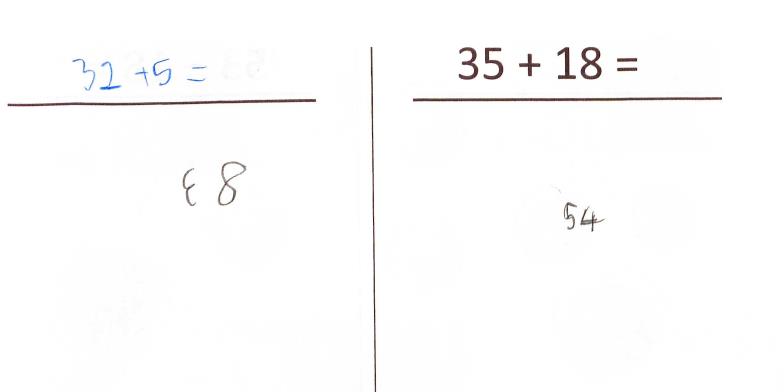
Abbildung 2:
Ausschnitt Eingangs-Standortbestimmung Zara „23+5“ und „35+18“
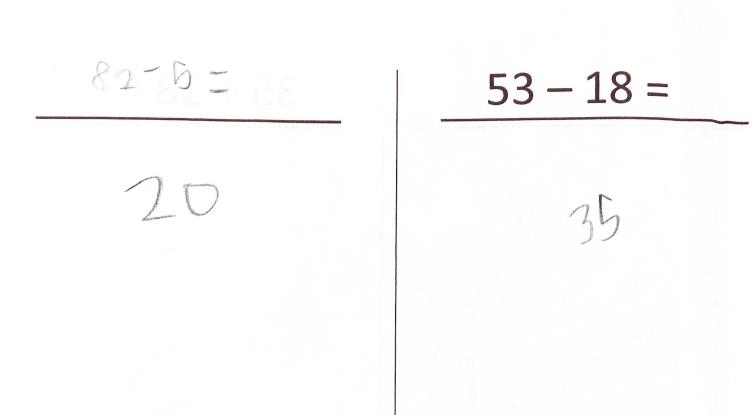
Abbildung 3:
Ausschnitt Eingangs-Standortbestimmung Zara „28-5“ und „53-18“
Aus der Analyse der Standortbestimmung konnten die Kompetenzen und Unterstützungsmöglichkeiten nicht eindeutig abgeleitet werden, weshalb mit Hilfe eines Leitfadens mit passenden Fragen und Aufgabenstellungen (vgl. Abb. 4) Diagnosegespräche geplant und durchgeführt wurden. Bei der Auswahl der Aufgaben wurde darauf geachtet, nicht nur die möglichen Schwierigkeiten, sondern auch bereits vorhandene Kompetenzen genauer beurteilen zu können.
Abbildung 4: Ausschnitt Diagnoseleitfaden Zara „Operationen“
Durchführung des Diagnosegesprächs
Entsprechend des dreiteiligen Ablaufs eines Diagnosegespräches (
s. Hintergrund) begann die Sitzung zunächst mit einem Einstieg. Die Lehrkraft klärte das Kind transparent über ihr Vorhaben auf (vgl. Video „Transparenz“;
s. Hintergrund; Leitprinzip 3 „Transparenz"), stellte ihm daraufhin ein paar einleitende Fragen (vgl. Video „Lieblingsfach“) und leitete dann zu einem Mathespiel (hier „Mister X“, vgl. Video „Mister X“) als motivierenden und spielerischen Einstieg über. Bei diesem Planungsschritt ist es wichtig, ein Spiel zu wählen, dass der Sicherung des Basisstoffs dient und im Idealfall auf den jeweiligen Förderschwerpunkt abgestimmt ist. Diese Vorgehensweise dient aber zugleich auch dem Herstellen einer angenehmen Gesprächsatmosphäre (
s. Hintergrund; Leitprinzip 2 „angenehme Gesprächsatmosphäre").
Bei Zara zeigten sich in der Standortbestimmung vor allem Unsicherheiten beim Addieren und Subtrahieren. Ausgehend von diesen Auffälligkeiten wurde für sie ein Diagnoseleitfaden zusammengestellt, der zum einen ihre schon vorhandenen Kompetenzen aufzeigen sollte, um eine sichere Grundlage zu haben, auf die in der Förderung aufgebaut werden kann (vgl. Wartha & Schulz, 2012). Zum anderen sollte herausgefunden werden, wie es zu den Unsicherheiten beim Durchführen der Operationen kommt.

Transparenz
Lieblingsfach
Mister X
Während des Diagnosegesprächs zeigte sich, dass Zara weder Probleme bei der ordinalen noch bei der kardinalen Vorstellung von Zahlen hat (vgl.
Zahlaspekte beachten). Bei der Durchführung verschiedener Zählaktivitäten zeigte sich, dass Zara beispielsweise problemlos im kleinen als auch im großen Zahlenraum zählen (vgl. Video „Zählen“) und Zahlen (quasi)-simultan erfassen konnte. Zudem war sie sicher in den Konventionen unseres Dezimalsystems, d.h. sie nutzte die 5er und 10er-Struktur des Rechenrahmens (vgl. Video „15 und 25 am Rechenrahmen“).
Zählen
15 und 25 am Rechenrahmen (mit Gebärdensprache und Untertitel)
Die Zerlegungen der Zehn konnte sie mit Unterstützung des Materials benennen. Ohne Material fiel auf, dass Zara manche Zerlegungen zwar schnell abrufen konnte, einige davon aber auch mit Fingern unter dem Tisch ermittelte und andere wiederum „falsch“ automatisiert hat (z.B. 7/4). Dies könnte ein Hinweis darauf sein, dass die Zerlegung zwar auswendig abrufbar ist, aber noch nicht als mentale Mengenvorstellung existiert (vgl. Video „Zerlegung der 10 – Phase 3“). Entsprechend des beschriebenen Verhaltens bei Diagnosegesprächen (s. Hintergrund; Leitprinzip 5 „Annahme von Rationalität) ließ die Lehrkraft diese Fehler zunächst stehen.
Auffällig waren auch die schon in der Standortbestimmung festgestellten Zahlendreher und das immer wieder auftretende Abzählen einzelner Perlen, auch beim Einstellen kleiner Zahlen (vgl. Video „Zahlendreher“). Ab und zu griff Zara aber auch schon auf Zahlzerlegungen zurück und nutzte sie handelnd am Material. Auffällig war dies besonders beim Einstellen von Zahlen am Rechenrahmen, an dem sie manchmal schon Kugeln bündelte und nicht immer alle einzeln abzählte (vgl. Video „Einstellen der 8 und der 23“).

Zerlegung der 10 - Phase 3
Zahlendreher
Einstellen der 8 und der 23
Beim Subtrahieren zeigte sich jedoch deutlich, dass Zara Ergebnisse auch im sehr kleinen Zahlenraum noch zählend ermittelte (vgl. Video „zählend rechnen“) und die Zerlegungen, die sie am Material nutzte, nicht auf das Rechnen im Kopf übertrug (vgl. Video „28-5 am Rechenrahmen“).

zählend rechnen
28 - 5 am Rechenrahmen
Reflexion des Diagnosegesprächs
Die Reflexion des Diagnosegesprächs fand mit Hilfe des ausgefüllten Diagnoseleitfadens (vgl. Abb. 5) statt.
Abbildung 5: Ausschnitt Diagnoseleitfaden Zara „Operationen“
Zara zeigte im Gespräch schon vielfältige Kompetenzen. Die Analyse der Aufzeichnungen ergab aber auch, dass sie vor allem beim Subtrahieren noch zählend rechnete und nicht auf Zahlzerlegungen zurückgriff. Da sie diese aber bereits teilweise nutzte, sobald sie am Material handeln konnte, bot es sich an, im Fördergespräch genau dort anzusetzen.
Fördergespräche
Vorbereitung des Fördergesprächs: Förderschwerpunkte und Leitfaden
Ausgehend von der Analyse des durchgeführten Diagnosegesprächs wurden erste Vermutungen über vorhandene Kompetenzen und Schwierigkeiten, aber auch über mögliche Unterstützungsmaßnahmen aufgestellt. Mit Zara wurden deshalb zunächst die Zahlzerlegungen der Zahlen von fünf bis zehn mit Plättchen thematisiert sowie aufgrund der auftretenden Zahlendreher das Einstellen von Zahlen am Rechenrahmen, unter Nutzung der thematisierten Zerlegungen, geübt (s. Hintergrund: Planungsschritte zur Vorbereitung auf Fördergespräche).
Tipp: Das Thema „Zahlzerlegungen“ wird im Teilmodul
„Beziehungen herstellen“ in der Rubrik Inhalte näher ausgeführt.
Beim Einstellen der Zahlen wurde Zara dazu angeregt, die Zahlzerlegungen systematisch zu nutzen anstatt jede Perle einzeln zu schieben. Dieses diente dazu, Zara immer mehr zum strategischen Rechnen zu motivieren und das zählende Rechnen allmählich abzulösen. Das Nutzen von Plättchen und Rechenrahmen war Zara schon aus dem Unterricht bekannt, weshalb an dieser Stelle an die Klassensituation angeknüpft und auf die bekannten Anschauungsmittel zurückgegriffen wurde. Zudem boten sich beide Materialien bei der Thematisierung der geplanten Inhalte an. Das Nutzen desselben Materials bei Diagnose- und Fördergesprächen ist zudem nicht nur für das Verständnis des Kindes sinnvoll, sondern stellt auch eine Entlastung für die Lehrkraft dar.
Entsprechend Zaras Schwierigkeiten wurden daraufhin passende Förderaufgaben (vgl. ‚Diagnose- und Förderaufgaben‘) in einem Leitfaden (s. Abb. 6) notiert. Dieser dient als Unterstützung zur Durchführung und Strukturierung eines Gesprächs.

Abbildung 6: Ausschnitt Leitfaden zum ersten Fördergespräch mit Zara (Vorbereitung)
Durchführung des Fördergesprächs
Entsprechend des dreiteiligen Ablaufs eines Fördergesprächs wurde zur Herstellung einer angenehmen Atmosphäre und als motivierender Einstieg zu Beginn jeder Fördersitzung mit Zara ein Mathespiel gespielt. Das Spiel orientierte sich am diagnostizierten Förderschwerpunkt (vgl. Video „Einstiegsspiel 9-er-Haus“) und diente der Sicherung der bisher erarbeiteten Zahlzerlegungen.
Einstiegsspiel 9er-Haus
Daraufhin wurde zur zweiten Sequenz des Fördergesprächs (s. Abb. 6) übergeleitet. Da Zara die Zahlzerlegungen am Material bereits erkannte, aber noch nicht beim Rechnen nutzte, sind diese Schwerpunkt der ersten Fördergespräche gewesen. Methodisch sollte zunächst an Ihren Kompetenzen angeknüpft und die Zerlegungen handelnd am Material thematisiert werden (vgl. Video „Handlung am Material und Sicht auf das Material“). Zur Verinnerlichung der Materialhandlung sollte im weiteren Schritt das Material verdeckt eingesetzt werden (vgl. Gaidoschik, 2014; s. auch Video „Verdeckter Materialeinsatz und Vorstellung im Kopf“).
Ab wann die Lehrkraft von der Materialhandlung zum verdeckten Materialeinsatz übergehen sollte, kann nicht eindeutig bestimmt werden. Dieser Verinnerlichungsprozess ist von Kind zu Kind unterschiedlich und kann mehrere Wochen dauern.

Handlung am Material und Sicht auf das Material
Verdeckter Materialeinsatz und Vorstellung im Kopf
Zum Initiieren einer mentalen Vorstellung bietet sich ein Arbeiten mit dem sog. Vierphasenmodell an, welches diesen Prozess vom konkreten zum gedanklichen Handeln unterstützen soll:
|
Phase |
Schwerpunkt |
|
1 |
 |
Das Kind handelt am geeigneten Material und erklärt, was es tut. |
|
2 |
 |
Das Kind beschreibt die Materialhandlung mit Sicht auf das Material. |
|
3 |
 |
Das Kind beschreibt die Materialhandlung ohne Sicht auf das Material. |
|
4 |
 |
Das Kind beschreibt die Materialhandlung „nur“ in der Vorstellung. |
Tabelle 7: Das Vierphasenmodell zum Aufbau von Grundvorstellungen
(Wartha & Schulz, 2012, S. 63)
Während das Kind in Phase 1 noch konkret am Material handelt und erklärt, was es tut, verfolgt und beschreibt es in Phase 2 den Handlungsprozess der Lehrkraft (oder eines Mitschülers) ohne selber aktiv zu sein. In Phase 3 wird dem Kind die Sicht auf das Material durch einen Sichtschutz genommen. Es muss nun ohne Sicht auf das Material genau beschreiben, was sein Partner hinter dem Sichtschutz sieht und machen soll. In der letzten Phase beschreibt das Kind die Materialhandlung dann ausschließlich in seiner Vorstellung, was erfordert, dass ein mentales Bild der Handlung vor dem geistigen Auge konstruiert werden muss (vgl. Wartha & Schulz, 2012).
Weitere Informationen zum Gebrauch des Vierphasenmodells finden sich bei PIKAS: Vierphasenmodell.
Der Gesprächsabschluss einer jeden Fördersitzung (s. Hintergrund ‚Ablauf eines Fördergesprächs‘) kann mit Hilfe eines Lerntagebuchs umgesetzt werden. Gemeinsam mit der Lehrkraft wird jede Sitzung reflektiert. Zaras Lernfortschritte wurden dabei von ihr selbst in schriftlicher Form festgehalten (vgl. Video „Lerntagebuch“; s. auch Abb. 7).

Lerntagebuch
Abbildung 7: Ausschnitt aus dem Lerntagebuch von Zara
Reflexion des Fördergesprächs
Anhand der Aufzeichnungen auf dem Leitfaden (s. Abb. 8) und der Reflexion des Gesprächs konnten Überlegungen zur weiteren Förderung getroffen werden.


Abbildung 8: Ausschnitt Leitfaden zum ersten Fördergespräch mit Zara (Reflexion)
Weitere Anregungen
Nachdem die Zahlzerlegungen von fünf bis zehn auch in Phase 3 und 4 vertieft wurden, konnte Zara im weiteren Verlauf der Förderung auch beim Einstellen und „Vorstellen“ von zusammengesetzten Zahlen auf diese zurückgreifen (vgl. Video „Einstellen von Zahlen am Rechenrahmen“). Aufgrund der anfänglich beobachteten Zahlendreher wurde mit Zara zwischendurch auch immer thematisiert, wie viele Zehner und Einer die entsprechende Zahl hat. Mittlerweile treten Zahlendreher gar nicht mehr auf.
Der nächste Schritt der Förderung besteht nun darin, diese Kompetenzen beim Durchführen von Operationen zu nutzen. In der weiteren Förderung wird mit Hilfe des Vierphasenmodells versucht, die Vorstellung von Zahlen zu vertiefen (Phase 3 und 4), sowie eine mentale Vorstellung der Operationen bei Zara zu initiieren (vgl. Video „Operationen am Rechenrahmen“).
Einstellen von Zahlen
Operationen am Rechenrahmen
Diese Methode kann auch gut in den Unterricht integriert werden, indem sich zwei Kinder entsprechend dieser Vorgehensweise gegenseitig Aufgaben stellen (vgl. ‚Diagnose- und Förderaufgaben’). So wird die Lehrkraft entlastet und die Selbstständigkeit der Schülerinnen und Schüler gefördert.
Nach einigen Fördersitzungen bietet es sich zudem an, die anfangs durchgeführte Standortbestimmung (vgl. Abb. 9; s. auch ‚Diagnose- und Förderaufgaben‘) noch einmal bearbeiten zu lassen, um den Nutzen der Förderung zu evaluieren und mit dem Kind gemeinsam die Lernfortschritte zu reflektieren sowie weitere Ziele (ggf. im Lerntagebuch) zu vereinbaren.
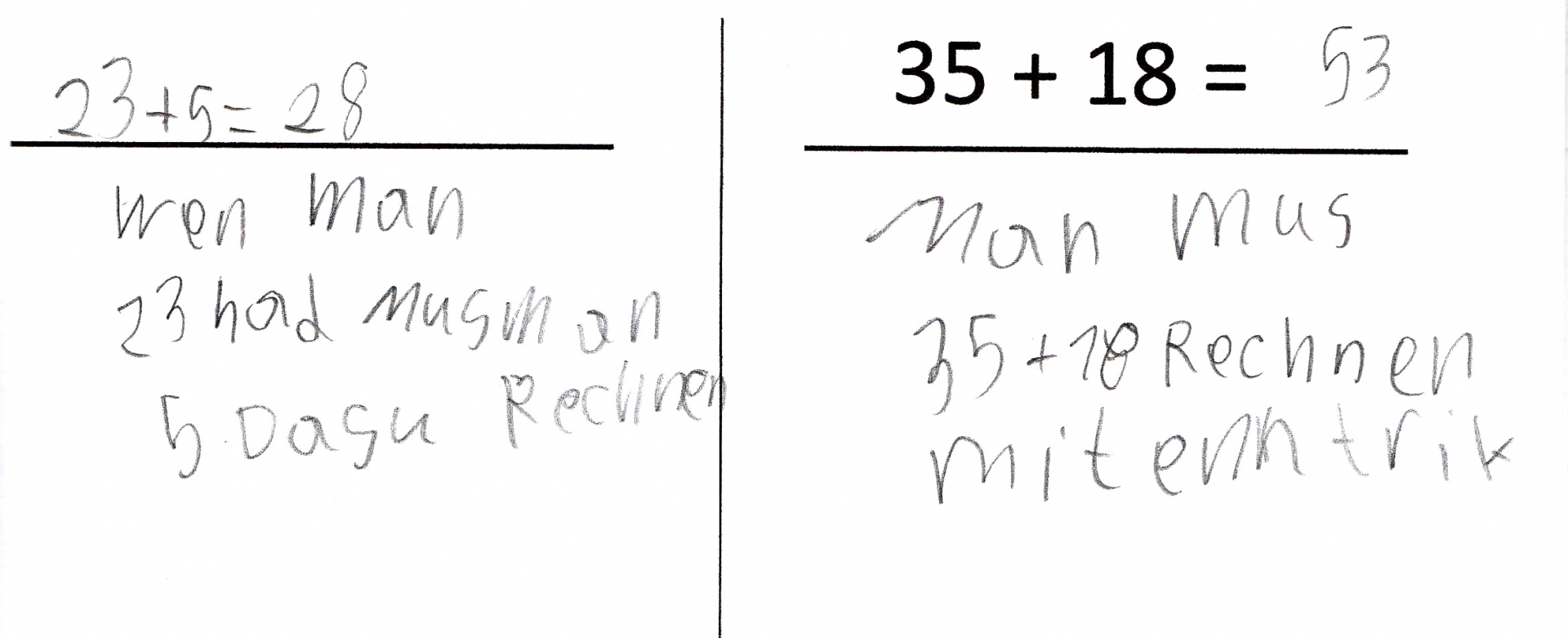
Abbildung 9: Ausschnitt Ausgangs-Standortbestimmung Zara „23+5“ und „35+18“