Carla, eine Schülerin aus dem zweiten Schuljahr, bearbeitet Additionsaufgaben im Zahlenraum bis 100. Das folgende Dokument zeigt einige von Carlas Ergebnissen:
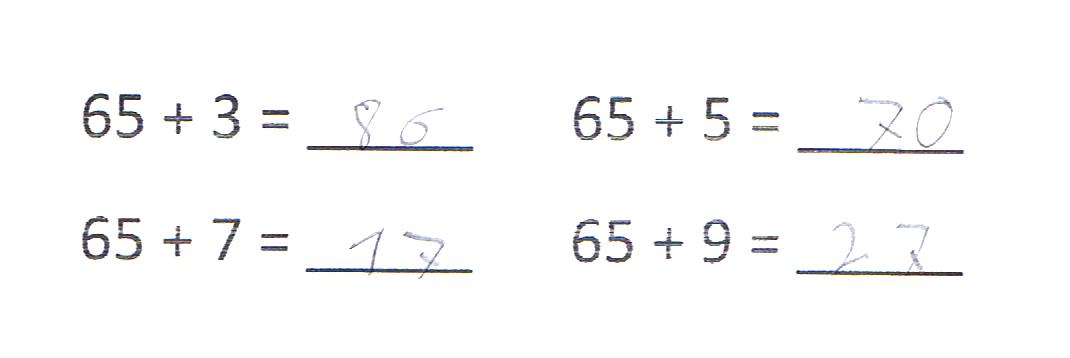
Abbildung 1: Lösungen von Carla zu Additionsaufgaben
Die erste Summe zeigt zunächst, dass Carla hier ein sogenannter Zahlendreher unterläuft. Diese fallen dem Klassenlehrer zunehmend regelmäßig bei der Durchsicht ihrer Dokumente auf. Bei der Lernprozessbegleitung legt er daher ein besonderes Augenmerk auf die Notation zweistelliger Zahlen.
Allerdings zeichnen sich bei obigen Ergebnissen auch Unsicherheiten bezüglich der Addition über eine Zehnerzahl hinweg ab, was sich insbesondere in den beiden unteren Aufgaben widerspiegelt.
Eigenaktivität
Haben Sie eine Vermutung, wie Carla ausgehend von 65 + 5 = 70 zu den beiden folgenden Ergebnissen gekommen sein könnte?
Insgesamt zeigt Carla zunehmend schwache Leistungen im arithmetischen Bereich. Da sie darüber hinaus ein sehr zurückhaltendes Kind ist, muss sie zu mündlichen Äußerungen häufig aufgefordert werden. Diese Situation ist ihr oft sichtbar unangenehm, wodurch eine detailliertere Erhebung der fachlichen Lernausgangslage allein basierend auf Diagnosemomenten und -gesprächen deutlich erschwert ist. Daraus ergibt sich für den fachfremd unterrichtenden Klassenlehrer eine Unsicherheit bezüglich diagnostischer Erkenntnisse.
Aus diesem Grund sucht er nach einem weiteren Weg, genauere Informationen über Carlas Denkwege und ihr mathematisches Verständnis zu erhalten. Denn nur mit einer Erfassung der arithmetisch kritischen Bereiche lässt sich eine darauf abgestimmte fachliche Förderung planen. Der diagnostische Prozess kann durch den Einsatz eines ausgewählten mathematikunterrichtbezogenen Testverfahrens unterstützt werden.
Eigenaktivität
Überlegen Sie selbst:
Was sollte ein Testverfahren „leisten“, damit Sie es in der geschilderten Situation einsetzen würden?