Gemeinsames Lernen durch Nutzung und Vernetzung verschiedener Forschermittel –
Die unterschiedlichen Funktionen von Forschermitteln im inklusiven Unterricht sinnvoll einsetzen
Alle drei Funktionen von Forschermitteln (s. Hintergrund) unterstützen für sich selbst betrachtet das Durchführen guten Mathematikunterrichts. Forschermittel können in nahezu jedem Themengebiet eingesetzt werden, weshalb im Folgenden darauf verzichtet wird, den Fokus auf eine spezielle Unterrichtsreihe zu richten. Stattdessen wird nachfolgend anhand von Kinderdokumenten ein kleiner Überblick darüber gegeben, wie Forschermittel für verschiedene Aufgabenformate und Themen sinnvoll und kompetenzübergreifend genutzt werden können.
Forschermittel am Beispiel der Hundertertafel
Die folgenden Dokumente entstammen einer Unterrichtsreihe zum Thema „Hundertertafel“ (vgl. ‚Verwandte Aufgaben‘). Interessant ist hierbei vor allem die Nutzung des Forschermittels „Pfeile“.
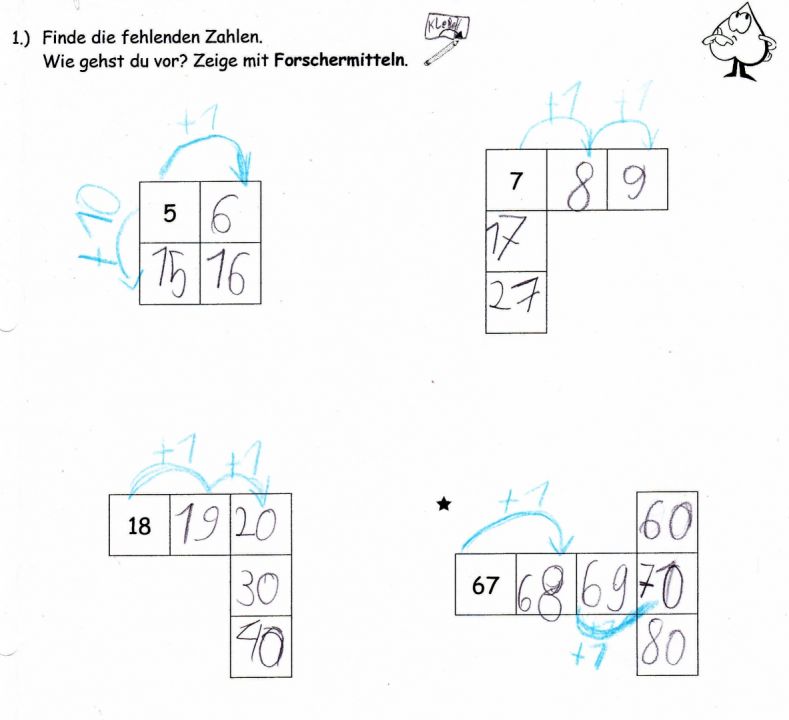 Abbildung 9
Abbildung 9
Dem Kind mit Unterstützungsbedarf im Bereich „Lernen“ dienten sie in erster Linie als Orientierungshilfe innerhalb der Hundertertafel und halfen ihm, die Einerschritte in den Zeilen und die Zehnerschritte in den Spalten selbstständig zu entdecken (Abb. 9).
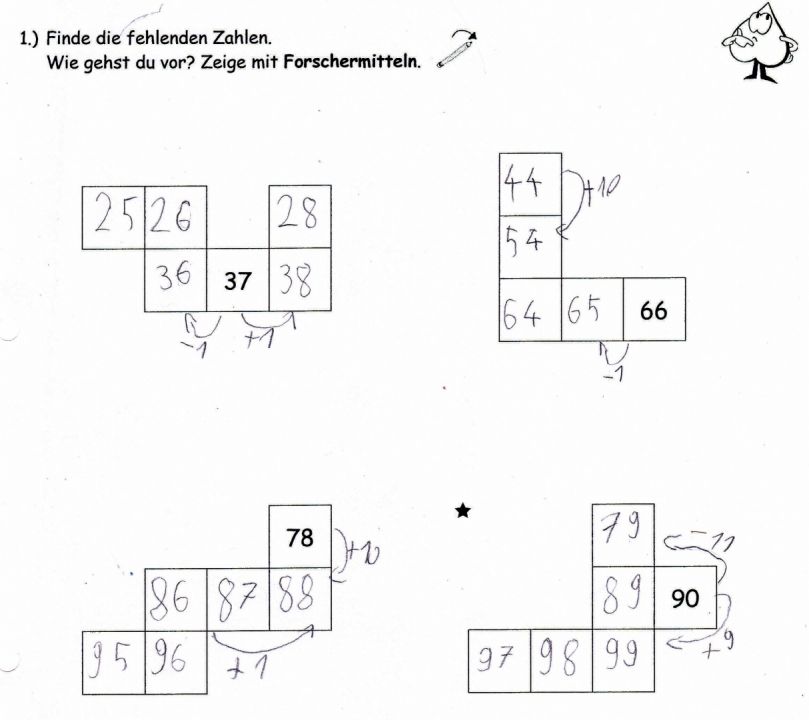 Abbildung 10
Abbildung 10
Das leistungsstärkere Kind hingegen nutzte die Pfeile primär als „Instrument des Kommunizierens“. Sie unterstützten ihn dabei, die gemachten Entdeckungen über Abhängigkeiten von horizontal, vertikal und auch diagonal liegenden Zahlen besser erklären zu können (Abb. 10).
 Abbildung 11
Abbildung 11
Auch eine nähere Betrachtung der Ergebnisse beim Auftrag „Was kannst du an der Hundertertafel alles entdecken?“ (vgl. ‚Offene Aufgaben‘) zeigt, wie leistungsschwächere und -stärkere Kinder ihren Nutzen aus den ihnen zur Verfügung stehenden Forschermitteln ziehen. Fast alle Schülerinnen und Schüler griffen zunächst auf Farben als Ausgangspunkt für ihre Entdeckungen zurück, mit denen es ihnen ermöglicht wurde, Auffälligkeiten innerhalb der Hundertertafel auch ohne Verschriftlichung festzuhalten (Abb. 11; Abb. 12). Das leistungsstärkere Kind schaffte es zudem, allein durch die Forschermittel „Pfeile“ und „Farben“, die Eigenschaften von Zeile, Spalte und Diagonale erklären zu können, was ihm die Verschriftlichung vermutlich erleichterte.
 Abbildung 12
Abbildung 12
Forschermittel am Beispiel von Quadratmehrlingen
Gerade geometrische Unterrichtsreihen, die den Fokus auf eine Handlungsorientierung im Sinne des Handelns mit sich anschließender Reflexion legen, profitieren vom Einsatz von Forschermitteln. Eine sinnvolle Möglichkeit Forschermittel zu verwenden, bietet beispielsweise eine Unterrichtsreihe zum Thema „Quadratmehrlinge“ (vgl. ‚Darstellungsformen‘).
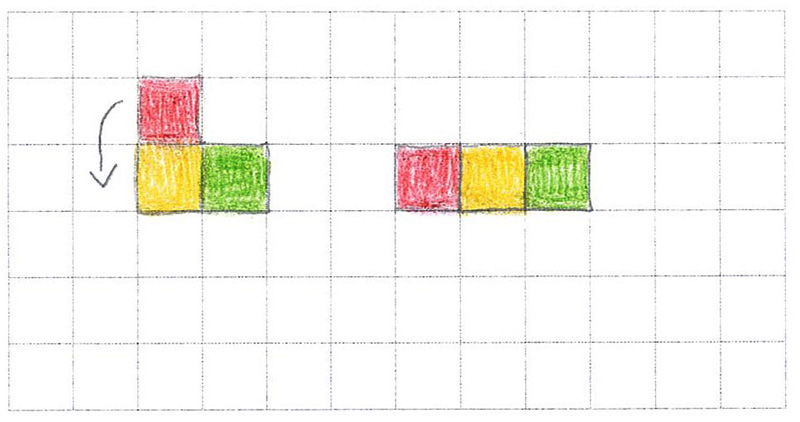 Abbildung 13
Abbildung 13
Ein Mädchen, das zum Zeitpunkt der Unterrichtsreihe nur wenig Deutschkenntnisse besaß, verdeutlichte mit einem Pfeil und unterschiedlichen Farben (Abb. 13), wie sie durch Verschiebung eines Quadrates einen weiteren Drilling gefunden hat. Allein durch die Verwendung der Forschermittel konnte sie so den anderen Kindern zeigen, was sie entdeckt hat.
 Abbildung 14
Abbildung 14
Ein anderes Kind (Abb. 14) verdeutlichte sein Vorgehen ebenfalls mit einem Pfeil, drückt durch ihn aber das Hinzufügen eines Quadrats zu einem bestehenden Domino (Zwilling) aus. Der Domino (lila) sowie das einzelne Quadrat (orange) wurden zum besseren Verständnis für die anderen Kinder auch farblich gekennzeichnet, was dabei half, die schriftliche sowie mündliche Erklärung zu unterstützen.
Forschermittel am Beispiel von Tauschaufgaben
Das Entdecken der Ergebnisgleichheit von Tauschaufgaben bei der Multiplikation ist ebenfalls eine gute Einsatzmöglichkeit für Forschermittel. Leistungsstarke Schülerinnen und Schüler erhalten mit ihnen die Möglichkeit, das Kommutativgesetz an exemplarischen Aufgaben zu verstehen und zu nutzen.
Bei den nachfolgenden Dokumenten, entnommen aus einer Unterrichtsreihe zum Thema „Besondere Malaufgaben“ (vgl. ‚Anforderungsbereiche‘), wird erst unter näherer Betrachtung ersichtlich, wie gewinnbringend der Einsatz von Forschermitteln wie Farben oder Einkreisen war.
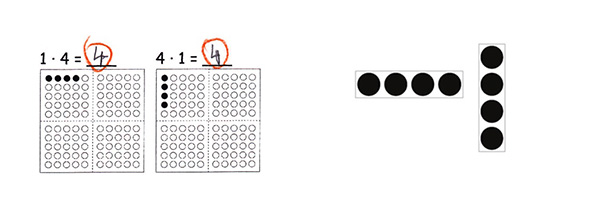 Abbildung 15
Abbildung 15
So konnte eine Schülerin zunächst keine Auffälligkeit beider Ergebnisse feststellen (Abb. 15). Das Forschermittel „Plättchen“ bzw. „Plättchenstangen“ ermöglichte es ihr aber in seiner Funktion als „Instrument des Entdeckens“, zwei Vierer-Plättchen haptisch aufeinanderzulegen, wodurch ihr die Ergebnisgleichheit erst bewusst wurde. Das anschließende Einkreisen war ebenfalls von Vorteil, da es ihre Entdeckung dokumentarisch festhielt und ihr erlaubte, sich in der Plenumsphase daran zu erinnern.
 Abbildung 16
Abbildung 16
Interessant ist auch eine nähere Betrachtung der eingesetzten Forschermittel eines Kindes mit erhöhtem Unterstützungsbedarf im Bereich Lernen (Abb. 16). Seine Antwort lässt auf wesentlich weniger Entdeckungen schließen, als er tatsächlich gemacht hat. Denn aufgrund der Verwendung des Forschermittels „Farben“ ist zu erkennen, dass er neben der Ergebnisgleichheit auch die Gleichheit der Faktoren erkannt hat.
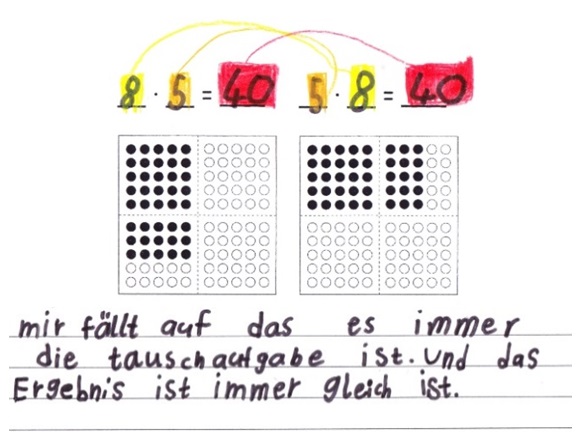 Abbildung 17
Abbildung 17
Eine leistungsstarke Schülerin benutzte ebenfalls die bereits genannten Forschermittel (Abb. 17). Zudem stellt sie durch Verbindungslinien und dem Einsatz gleicher Farben eine Beziehung der Aufgaben her, womit die Struktur der Tauschaufgabe ersichtlich wird und als „Instrument des Kommunizierens“ diente.
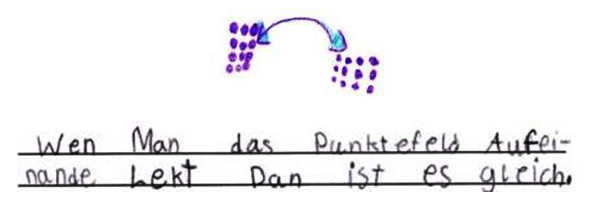 Abbildung 18
Abbildung 18
Dass selbst ein mathematischer Beweis unter Verwendung von Forschermitteln möglich ist, zeigt das oben stehende Kinderdokument (Abb. 18). Mittels gezeichneter Plättchen bzw. Punktefelder und der Verwendung eines Pfeils verbildlicht das Kind die Deckungsgleichheit beider Ergebnisse und schafft es so, das Kommutativgesetz der Multiplikation am Beispiel zu erklären.
Forschermittel am Beispiel von Zahlenmauern
Der Einsatz von Forschermitteln erweist sich auch beim Aufgabenformat „Zahlenmauern“ (Müller & Wittmann, 2012) als sinnvoll, da es vielfältige Entdeckungsmöglichkeiten bietet, wie beispielsweise die Auswirkungen operativer Veränderungen näher zu untersuchen (vgl. ‚Tipps und Herausforderungen‘).
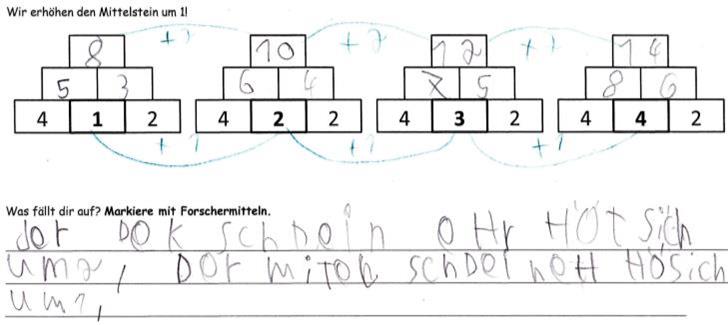 Abbildung 19
Abbildung 19
Das Nutzen von Pfeilen half einem Schüler mit erhöhtem Unterstützungsbedarf im Bereich Lernen, wichtige Wertänderungen des Decksteins zu erkennen und diese auch auf die folgenden Zahlenmauern zu übertragen (Abb. 19).
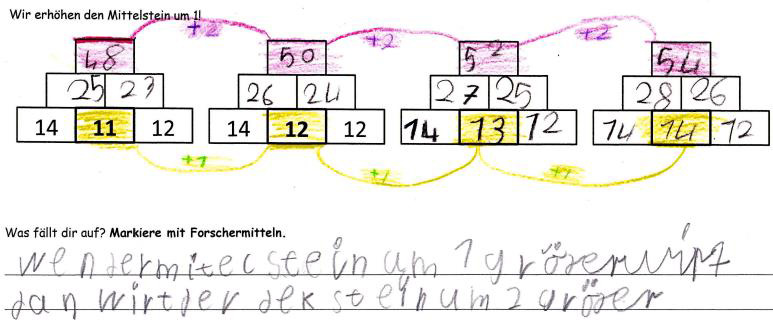 Abbildung 20
Abbildung 20
Ein leistungsstärkeres Kind erzeugte durch die Forschermittel „Pfeile“ und „Farben“ eine visuelle Hervorhebung der zu betrachtenden Steine. Das dadurch erkennbare Schema ist selbsterklärend und konnte im weiteren Verlauf der Stunde als Kommunikationshilfe genutzt werden (Abb. 20).
 Abbildung 21
Abbildung 21
Auch Abbildung 21 zeigt, dass Plättchen nicht nur als Unterstützungsmöglichkeit für leistungsschwächere Kinder Anwendung finden sollten, sondern auch von leistungsstärkeren Kindern, beispielsweise zum Beweisen, genutzt werden können. Im abgebildeten Beispiel nutzt das Mädchen die Plättchen, um mit ihnen einen Beweis aufzustellen: Sie versucht zu erklären, warum sich bei einer Erhöhung des Mittelsteins um 1, der Deckstein um 2 erhöht.
Weitere Anregungen
Forschermittel eignen sich bei nahezu allen Aufgabenstellungen und sollten von jedem Kind, egal ob leistungsstark oder leistungsschwach, durchgängig genutzt werden.
Vor allem dann, wenn wichtige mathematische Strukturen innerhalb eines Aufgabenformats entdeckt werden können, ist ihre Verwendung in der Unterrichtspraxis empfehlenswert.
Als Anregung wäre beispielsweise eine Unterrichtsreihe zum Thema „Rechendreiecke“ (Abb. 22) zu nennen. Gleichbleibende oder sich regelmäßig verändernde Zahlen können mit Forschermitteln markiert oder fehlende Zahlen mit Hilfe von Plättchen oder Zahlenkarten gefunden werden.
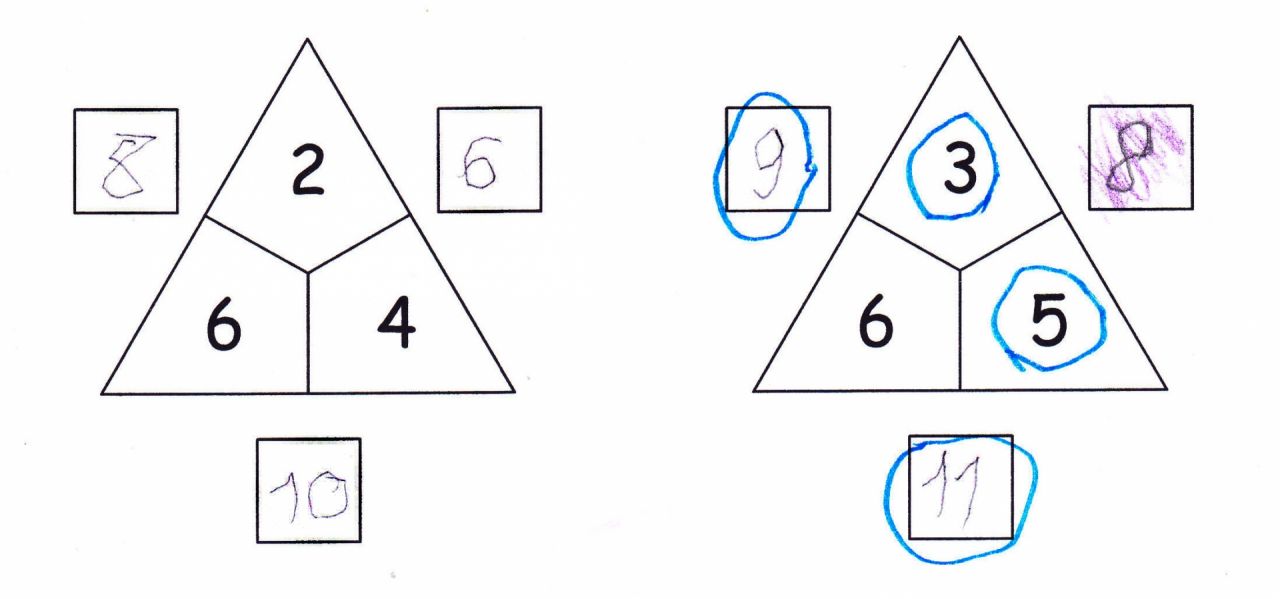 Abbildung 22
Abbildung 22
Weitere Ideen zur Benutzung von Forschermitteln im Unterricht sind in einer ausführlichen Unterrichtsreihe zum Aufgabenformat „Entdeckerpäckchen“ (Abb. 23) bei PIKAS (vgl. PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Fortbildungsmaterial – PIK fördern; s. auch PIKAS 2012, S. 36 ff.) zu finden.
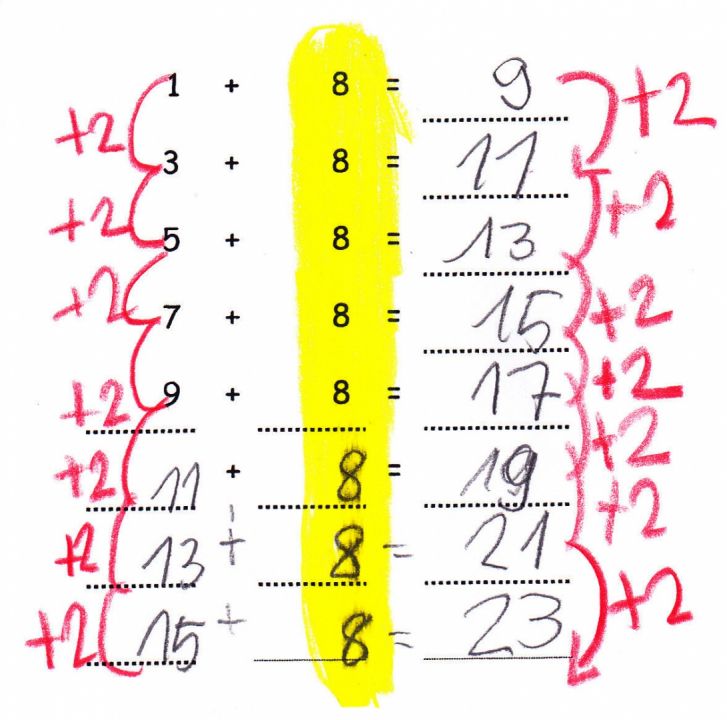 Abbildung 23
Abbildung 23