Einstieg

Spiegel & Selter (2004, S. 22) haben diese Aufgabe mehreren hundert Erwachsenen gestellt und sie gebeten, ihre Rechenwege festzuhalten.

Erstaunlicherweise gab es insgesamt 19 verschiedene Vorgehensweisen, von denen im Folgenden (Abb. 1) nur eine kleine Auswahl dargestellt ist:

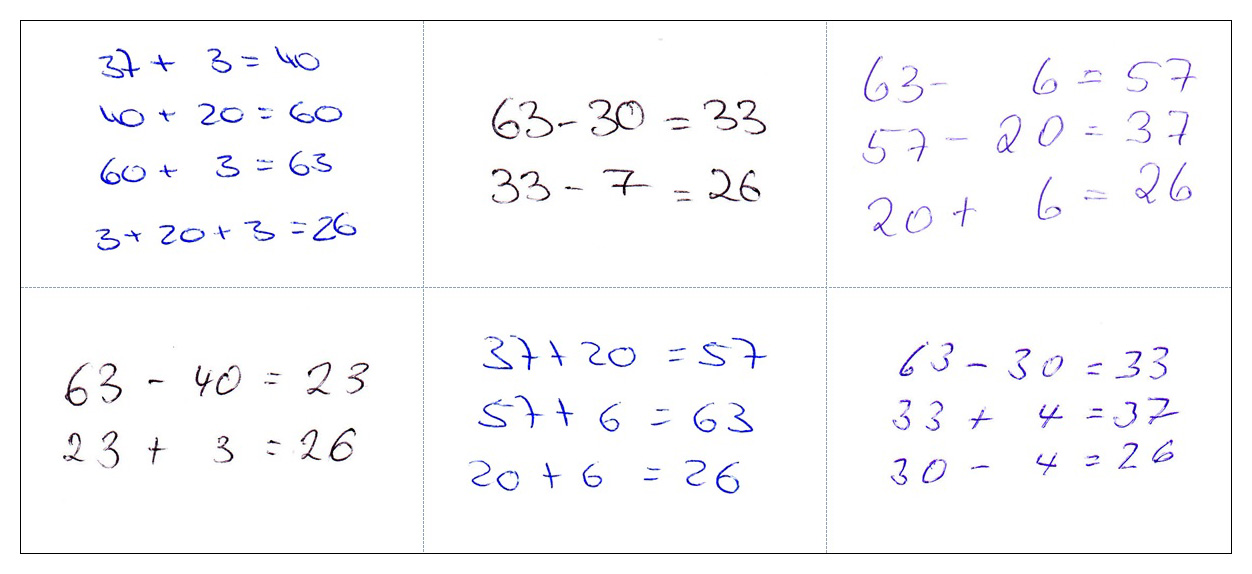
Ist Ihr Rechenweg auch dabei? Können Sie die Vorgehensweisen der anderen nachvollziehen und ihre Sinnhaftigkeit verstehen? Das Versuchsergebnis zeigt etwas ganz Essentielles: Jede und jeder rechnet anders.

Was man bei Erwachsenen beobachten kann, trifft auch auf Kinder zu.
Doch obwohl die Pädagogik in den letzten Jahrzehnten vermehrt der Heterogenität innerhalb von Lerngruppen Beachtung schenkt („Pädagogik der Vielfalt“), wird die Vielfalt mathematischen Denkens der Lernenden  immer noch zu wenig berücksichtigt.

So ist es vor allem im Mathematikunterricht oft noch gängige Praxis, Aufgaben zu stellen, die es nach einem ganz bestimmten Schema zu lösen gilt. Oft wird es gerade leistungsschwächeren Kindern nicht zugetraut, mehrere Verfahren zu beherrschen, da vermutet wird, dass eine Thematisierung „komplexerer“ Strategien für sie eine Überforderung darstellen könnte.

Warum es aber wichtig und notwendig ist, Lernenden verschiedene Vorgehensweisen zumindest zu ermöglichen, wenngleich auch nicht von ihnen zu verlangen, wird auf den folgenden Seiten näher erläutert.