Gemeinsames Lernen durch verschiedene Vorgehensweisen – Vertiefung der halbschriftlichen Subtraktion durch vorteilhaftes Nutzen unterschiedlicher Rechenwege
Ein konkretes Beispiel für Aufgaben, bei denen sich das Thematisieren von verschiedenen Vorgehensweisen gut eignet, entstammt einer Unterrichtsreihe zum Thema „Unsere Rechenwege bei Minusaufgaben“.
Im Vorfeld dieser Unterrichtsreihe wurde analog zur halbschriftlichen Addition (vgl. KIRA: Arithmetik – Halbschriftliches Rechnen – Addition – Halbschriftliche Addition) die halbschriftliche Subtraktion (vgl. KIRA: Arithmetik – Halbschriftliches Rechnen – Subtraktion – Halbschriftliche Subtraktion) eingeführt. Daraufhin folgte eine Unterrichtseinheit zur Vertiefung von Rechenwegen bei Additionsaufgaben („Unsere Rechenwege bei Plusaufgaben“), in der unterschiedliche Vorgehensweisen benannt und von den Kindern je nach Präferenz ausprobiert wurden. Die Rechenwege wurden anschließend unter dem Gesichtspunkt ihrer jeweiligen Vor- und Nachteile bei verschiedenen Aufgabentypen zur Diskussion gestellt (vgl. Müller & Wittmann, 2012).
Die Dokumente der durchgeführten Unterrichtsreihe stammen aus einer aus 30 Schülerinnen und Schülern bestehenden zweiten Schulklasse mit sehr heterogenen Lernvoraussetzungen. In der inklusiven Lerngruppe befinden sich u.a. Kinder mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ und sonderpädagogischem Unterstützungsbedarf im „sozial-emotionalen Bereich“ sowie im Bereich „Sprache“. Die Klasse weist zudem einen hohen Anteil von Kindern auf, die Deutsch als Zweitsprache lernen.
Die folgenden Kinderdokumente sind der Untereinheit „Unsere Rechenwege bei Minusaufgaben“ entnommen, dessen Zielsetzung darin bestand, auf Grundlage verschiedener Minusaufgaben (analog zur Addition) das Verständnis für Rechenwege zu vertiefen. Nicht nur die inhaltsbezogenen, sondern auch die prozessbezogenen Kompetenzen standen hierbei im Zentrum (vgl. KIRA: Problemlösen & Co – Prozessbezogene Kompetenzen fördern – Schöne Päckchen). Als Ausgangspunkt wurden die Aufgabenstellungen des folgenden Arbeitsblattes (s. Abb. 10) genutzt, welches bei Bedarf auch durch Aufgaben eines niedrigeren Zahlenraumes mit verwandter Aufgabenstellung z.B. 17-13 oder 21-19 modifiziert werden kann (vgl. ‚Verwandte Aufgaben‘). Dies erwies sich insbesondere in dieser Unterrichtsstunde als durchaus sinnvoll, da es als Zielsetzung galt, Diskussionsbedarf über den Sinn und Zweck unterschiedlicher Vorgehensweisen zu schaffen, anstatt den Fokus auf einen alleinigen Vergleich von Ergebnissen zu richten.
Letzteres wurde in der konkreten Unterrichtsstunde auch dadurch verhindert, dass die Kinder zunächst nur die erste Aufgabe des Arbeitsblattes („Rechne die Aufgabe 57-23 möglichst geschickt.“) lösen sollten und nicht mit einer Fülle von Subtraktionsaufgaben überhäuft wurden. Auch die Formulierung „möglichst geschickt“ impliziert bei ihnen über den selbst gewählten Rechenweg zu reflektieren. Anzumerken sei an dieser Stelle, dass Kinder die Aufforderung „möglichst geschickt“ zu rechnen anders verstehen können, bspw. lediglich als sicher. Es ist daher ratsam, die Wortbedeutung mit den Kindern gemeinsam zu erarbeiten und sich auf eine sinnvolle „Auslegung“ des Begriffs zu einigen.
 Abbildung 10
Abbildung 10
In der praktischen Anwendung im Unterricht konnte beobachtet werden, dass durch den nicht vorgegebenen Problemlöseweg deutlich mehr Kinder angesprochen wurden und motivierter waren, eine passende Lösung zu finden. Da ihnen mittlerweile diverse Rechenwege bekannt waren, wurden diese nun, je nach Präferenz auf vielfältige Weise genutzt.
Die meisten Schülerinnen und Schüler nutzten verschiedene halbschriftliche Vorgehensweisen auf symbolischer Ebene. Dabei ließ sich die Anwendung von drei grundsätzlichen Strategien feststellen: „Stellenweise“ (vgl. Abb. 11-12), „Schrittweise“ (vgl. Abb. 13-14) und „Vereinfachen“ (vgl. Abb. 15). Aufgrund der offenen Aufgabenstellung „Beschreibe deinen Rechenweg“ wurde zudem jedes Kind darin bekräftigt, seine Vorgehensweise schriftlich zu beschreiben (vgl. ‚Offene Aufgaben‘).
Je nach Leistungsniveau wurde diese Möglichkeit anders genutzt, sei es um die verwendete Strategie zu benennen, das konkrete Beispiel schriftlich zu erläutern oder einen Versuch zu wagen, den gewählten Rechenweg unter Zuhilfenahme von Fachwörtern in eine allgemeine Form zu bringen (vgl. ‚Anforderungsbereiche‘).
 Abbildung 11: Vorgehensweise „Stellenweise (Z-Z, dann E-E)“
Abbildung 11: Vorgehensweise „Stellenweise (Z-Z, dann E-E)“
 Abbildung 12: Vorgehensweise „Stellenweise (E-E, dann Z-Z)“
Abbildung 12: Vorgehensweise „Stellenweise (E-E, dann Z-Z)“
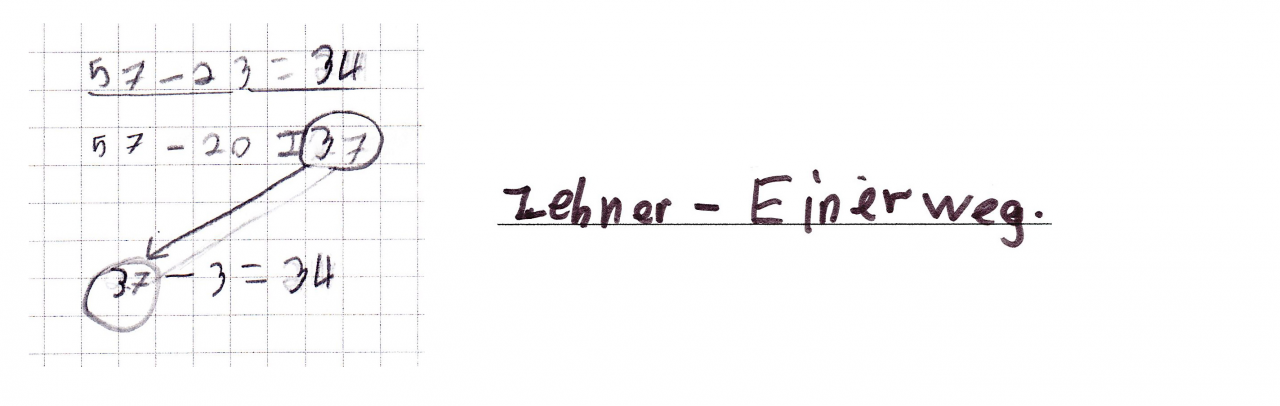 Abbildung 13: Vorgehensweise „Schrittweise (ZE-Z dann -E)“
Abbildung 13: Vorgehensweise „Schrittweise (ZE-Z dann -E)“
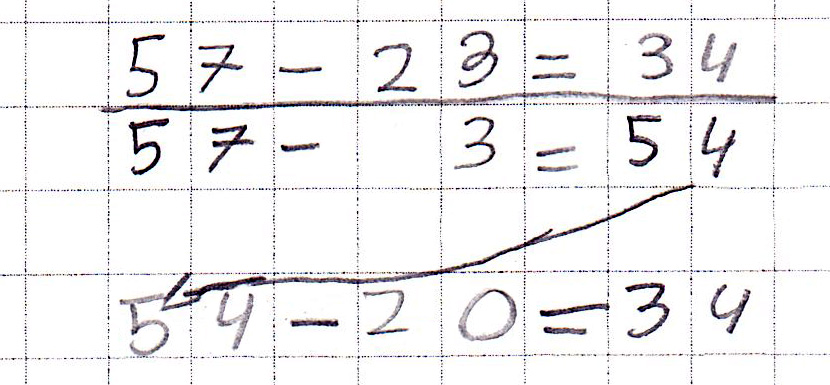 Abbildung 14: Vorgehensweise „Schrittweise (ZE-E dann -Z)“
Abbildung 14: Vorgehensweise „Schrittweise (ZE-E dann -Z)“
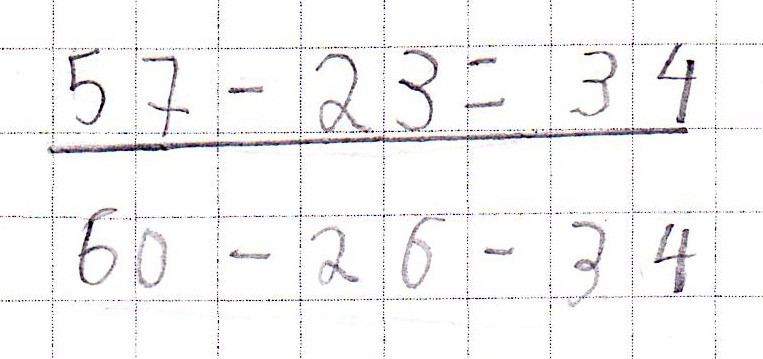 Abbildung 15: Vorgehensweise „Vereinfachen“
Abbildung 15: Vorgehensweise „Vereinfachen“
Die Wahl der Vorgehensweise ließ den Kindern für ihre Problemlösestrategie auch die Nutzung weiterer Darstellungsformen (vgl. ‚Darstellungsformen‘) zu. Größtenteils wurde hierbei auf die Verwendung des Rechenstrichs zurückgegriffen, anhand dessen vor allem die schrittweise Subtraktion verdeutlicht wurde (vgl. Abb. 16-18). Die Beschreibungen der Rechenwege lassen aufgrund ihrer Ausformulierungen erahnen, dass der Rechenstrich meistens bei leistungsstärkeren Kindern Anwendung fand.
 Abbildung 16: Vorgehensweise „schrittweise“ am Rechenstrich
Abbildung 16: Vorgehensweise „schrittweise“ am Rechenstrich
 Abbildung 17
Abbildung 17
 Abbildung 18
Abbildung 18
Auch leistungsschwächere Kinder fanden Vorgehensweisen, mit der sie die Aufgabe lösen konnten. Das Kind mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ nutzte die bildliche Darstellung von Zehnerstangen und Plättchen, welche ihm eine „stellenweise“ Subtraktion ermöglichte (vgl. Abb. 19). Es fällt auf, dass ihm das halbschriftliche Subtrahieren auf symbolischer Ebene noch Probleme bereitete, da es seinen Rechenweg auch in der Beschreibung nicht konkret erklären, sondern die Methode nur benennen konnte.
Die durch das Material initiierte Strategie ermöglichte dem Jungen aber trotzdem einen Lernerfolg, den er mit der Aufforderung, einen konkreten halbschriftlichen Rechenweg zu nutzen, vermutlich nicht hätte erreichen können. Zu diesem Zeitpunkt konnte er seinen Rechenweg in der Plenumsphase einbringen und den anderen Kindern als seine Vorgehensweise vorstellen, an welche die anderen Lernenden anknüpfen konnten. Für seine weitere Entwicklung wurden für den Schüler gemeinsam mit der Sonderpädagogin weitere Fördermaßnahmen zum Aufbau von Zahl- und Operationsvorstellungen erarbeitet. Mit Hilfe des sog. Vierphasen-Modells (vgl. Wartha & Schulz, 2014) sollte an seine Vorgehens- und Darstellungsweise mit Hilfe von Plättchen angeknüpft werden, um eine Vorstellung der Operation im Kopf zu entwickeln (vgl. ‚Diagnose- und Fördergespräche‘).
 Abbildung 19: „Nutzung von Darstellungsmitteln (Plättchen)“
Abbildung 19: „Nutzung von Darstellungsmitteln (Plättchen)“
Die genauere Betrachtung der Kinderdokumente zeigt auch hier wieder den wesentlichen Vorteil bei der Ermöglichung verschiedener Vorgehensweisen: Ist das Lösen eines mathematischen Problems nicht auf eine bestimmte Vorgehensweise beschränkt, kann den Kindern der Zugang zur jeweiligen Aufgabe erleichtert werden.
Leistungsstarke Kinder werden dahingehend gefordert, ausgehend von ihrem Repertoire an möglichen Lösungsstrategien, die Vor- und Nachteile bestimmter Vorgehensweisen zu entdecken, um die für sich geeignetste Herangehensweise zweckmäßig einsetzen zu können („flexibles Rechnen“). Auf der anderen Seite wird Schülerinnen und Schülern mit Unterstützungsbedarf der Zugang zur jeweiligen Aufgabe erleichtert, da sie ihre eigenen Denkwege nutzen können. Hierbei ist noch festzuhalten, dass nicht alle Kinder zwingend alle Strategien beherrschen müssen, da das Nachvollziehen anderer Rechenwege auch eine zusätzliche Herausforderung darstellen kann.
So wesentlich die Verwendung von präferierten Vorgehensweisen auch ist: Ebenso wichtig ist die anschließende Diskussion über ihre Sinnhaftigkeit. Wird dies vernachlässigt, besteht die Möglichkeit, dass sich einzelne Kinder zu sehr auf eine Strategie beschränken und den eigentlichen Vorteil in der Anwendung unterschiedlicher Vorgehensweisen aus den Augen verlieren.
Eine Diskussion über die sinnhafte Anwendung derselben Strategie bei der zweiten Subtraktionsaufgabe (41-39) wirkt dem Ganzen als erster Schritt in der folgenden Unterrichtsstunde entgegen. Aufgrund des Zehnerübergangs der Einerstelle kann man als Lehrkraft sehr gut auf mögliche Schwierigkeiten der stellenweisen Subtraktion hinweisen und ein Gespräch über mögliche alternative Vorgehensweisen anregen.
Weitere Anregungen
Unterschiedliche Rechenwege zu thematisieren, ist für alle Grundrechenarten von Bedeutung und daher auch in den nachfolgenden Schuljahren ein essentieller Bestandteil des Unterrichts. Analog zur vorgestellten Unterrichtsreihe können beispielsweise im 3. und 4. Schuljahr die verschiedenen Möglichkeiten beim Dividieren thematisiert werden (vgl. KIRA: Arithmetik – Halbschriftliches Rechnen – Division – Halbschriftliche Division).
Zahlreiche Unterrichtsanregungen finden Sie auf der Homepage unseres Partnerprojekts PIKAS: Haus 5: Lernen auf eigenen Wegen – Unterrichtsmaterial.
Ein weiterer Vorteil, der die Nutzung unterschiedlicher Vorgehensweisen mit sich bringt, ist zudem die Möglichkeit, im Plenum über die Sinnhaftigkeit einiger Lösungsstrategien in Bezug zur konkreten Aufgabenstellung zu diskutieren, um die Problemlöse- und Argumentationskompetenz der Schülerinnen und Schüler durch gezielte Auseinandersetzungen mit den Rechenwegen anderer Kinder zu erweitern.
Des Weiteren sind unterschiedliche Herangehensweisen auch bei geometrischen Themen möglich, indem beispielsweise verschiedene Vorgehensweisen zum Finden von Quadratmehrlingen thematisiert werden (vgl. ‚Darstellungsformen‘).
Eine weiterführende Unterrichtsreihe zur Hundertertafel (vgl. ‚Verwandte Aufgaben‘) bietet sich in der dritten Klasse an, in der das Bilden von Summen auf der Hundertertafel (oder auch im Tausenderbuch) thematisiert werden kann. Auch hier können verschiedene Vorgehensweisen genutzt werden (PIKAS: Haus 2: Langfristige Lernprozesse – Unterrichtsmaterial – Vierersummen).
Beispielhafte Anregungen, wie „herkömmliche" Aufgabenstellungen angepasst werden können, so dass sie verschiedene Vorgehensweisen ermöglichen, finden sich hier:
Anregungen zum Ermöglichen verschiedener Vorgehensweisen