Im Zentrum dialogischer Lernumgebungen steht das „Bemühen um ein wechselseitiges Verstehen und Verstanden werden“ (Bauersfeld, 2002, 12) aller Beteiligten. Im konkreten Austausch über mathematische Produkte oder Vorgehensweisen setzt dies – wie im Eingangstext dargestellt – auf der Seite des „Verstandenwerdens“ die Bewusstmachung, Klärung und verständliche Darstellung eigener Gedanken (vgl. Korten, 2020) voraus.
 Abbildung 2 - Mit und voneinander lernen
Abbildung 2 - Mit und voneinander lernen
Die eigenen Ideen und Vorstellungen werden sowohl in der Vorbereitung als auch im Austausch selbst kontinuierlich weiterentwickelt, in dem sie zunehmend konkretisiert, systematisiert und dokumentiert werden. Den eigenen Gedanken auf die Spur kommen die Lernenden also gerade in dialogischen Lernsituationen, in denen sie angeregt werden, sich über Lösungsprodukte oder -wege auszutauschen.
Deshalb kommt der Auswahl von austauschanregenden Aufgaben besondere Bedeutung zu. Im folgenden Exkurs soll daher knapp dargestellt werden,
-
welche Merkmale solche austauschanregenden Aufgaben aufweisen sollten,
-
inwieweit sie die Lernenden eher anregen, sich über ihre Produkte oder über ihre Vorgehensweisen auszutauschen, und
-
mit welchen Entdeckungen die Lehrkraft rechnen kann.
Exkurs: Austauschanregende Aufgaben
Merkmale
Eine wesentliche Grundlage für kooperativ-kommunikative Lernsituationen bilden Aufgaben, die durch eine gemeinsame Orientierung und Problementfaltung auch einen gemeinsamen Austausch erlauben.
Erreicht werden kann dies durch…
-
substantielle Aufgabenformate, die natürliche Differenzierung zulassen (vgl. Wittmann & Müller, 2004, siehe auch Aufgaben adaptieren) und eine Ausgangsaufgabe für alle Lernenden besitzen,
-
eine vergleichsweise niedrige Eingangsschwelle, die „es allen Kindern ermöglicht, einen ersten Zugang zu finden und an einer ihnen möglichen Stelle in eine Auseinandersetzung mit der Sache zu treten“ (Krauthausen & Scherer, 2014, 53),
-
sogenannte „Rampen“ (ebd.) in der Aufgabenstellung, wodurch sich das Anspruchsniveau hochregeln lässt („Finde geschickt…“, oder „Hast du alle gefunden?“),
-
zahlreiche Freiheitgrade in der Bearbeitung, beispielsweise in Bezug auf Umfang und Komplexität der Lösung, Verwendung von Hilfs- oder Arbeitsmitteln, der Art und Weise der Darstellung des Vorgehens und der Lösungen (vgl. ebd.), die eine individuelle Bearbeitung der Problemstellung ermöglichen.
Aufgaben, die diese austauschanregenden Merkmale aufweisen, schaffen zahlreiche Diskussionsanlässe. Thematisiert werden können z.B. …
-
die unterschiedlichen Bearbeitungswege, Lösungen und deren Darstellungen, die Beschreibungen dieser („Beschreibe, wie du vorgegangen bist!“) oder Begründungen („Hast du alle gefunden?“) oder
-
die unterschiedlichen Deutungen dieser Vorgehensweisen und Lösungen, die im gemeinsamen Austausch zur Erweiterung bzw. Ergänzung der eigenen Handlungs- und Deutungsschemata der Lernenden beitragen können (vgl. Brandt & Nührenbörger, 2009).
Zudem ist eine Diskussion über die gesammelten Erfahrungen und Erkenntnisse insgesamt naheliegend (anders als bei vereinzelten, individuellen Aktivitäten), weil die gesamte Lerngruppe am selben Problemkontext gearbeitet hat.
Fokus des Austausches: Produkte oder Vorgehensweisen
Mathematische Austauschprozesse können über Produkte der Lernenden oder über deren Vorgehensweisen stattfinden. Diese Unterscheidung ist für die Aufgabenstellung und -struktur sowie für mögliche Anregungen und Unterstützungen der Schülerinnen und Schüler von Bedeutung.
Zur Illustration dieser Unterscheidung werden Aufgabenstellungen zu einer Unterrichtsreihe zum Thema „Sechslinge“ (eine Form der Polyominos: Quadratmehrlinge) formuliert. Polyominos sind ebene Figuren, die durch das Aneinanderlegen von kongruenten Quadraten auf der Grundlage bestimmter Legeregeln entstehen (ausführliche Informationen unter Aufgaben adaptieren > Darstellungsformen > Unterricht).
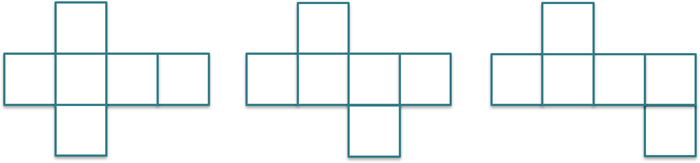 Abbildung 3 - Beispiele für verschiedene Sechslinge
Abbildung 3 - Beispiele für verschiedene Sechslinge
Produkte
Hier besteht das Ziel im Kennenlernen der individuellen Arbeitsprodukte der Mitschülerinnen und Mitschüler und in der daran orientierten gemeinsamen Weiterarbeit. Dabei ist es von Bedeutung, dass alle Produkte der Lernenden gewürdigt werden und die ggf. sehr unterschiedlichen Arbeitsergebnisse für sinnstiftende und produktive Austauschprozesse genutzt werden können.
Eine mögliche gemeinsame Ausgangsaufgabe könnte folgendermaßen aussehen:
1. Finde möglichst viele verschiedene Sechslinge!
2. Sind alle deine Sechslinge verschieden? Begründe!
Nachdem die Lernenden diese Aufgaben für sich bearbeitet haben, können sie mittels der übergeordneten Fragestellung ‚Welche Sechslinge habt ihr gefunden?‘ die folgenden Arbeitsaufträge gemeinsam weiterführend bearbeiten.
3. Vergleicht! Welche Sechslinge sind gleich, welche sind verschieden?
4. Sind das alle? Findet Sechslinge, die noch fehlen!
Dabei werden die einzelnen Produkte der Lernenden (in diesem Fall die gefundenen Sechslinge) in den Fokus des Austausches gerückt.
Vorgehensweisen
Wenn die Vorgehensweisen fokussiert werden sollen, besteht das Ziel des Austausches in der Reflexion des eigenen Vorgehens und im Kennenlernen und Nachvollziehen von Vorgehenswesen und Lösungswegen der Mitschülerinnen und Mitschüler.
Die Ausgangsaufgabe könnte dann folgendermaßen aussehen:
1. Finde verschiedene Sechslinge! Gehe möglichst geschickt vor.
2. Wie findest du einen neuen Sechsling?
Das „Wie“ in der 2. Aufgabe ist für den Fokus auf die Vorgehensweisen von Bedeutung, da es die mathematisch-inhaltliche Reflexion über das eigene Vorgehen anregt. Die darauffolgende Phase des gemeinsamen Austausches sollte unter der Fragestellung ‚Wie seid ihr vorgegangen?‘ stehen. Entsprechend geeignete gemeinsame Aufgabenstellungen können wie folgt lauten:
3. Erklärt, wie ihr neue Sechslinge gefunden habt!
4. Schreibt gemeinsam Tipps auf, wie man geschickt neue Sechslinge findet!
Welche Entdeckungen kann ich erwarten?
In der Praxis sehen Kinder „oft viel mehr als von der Lehrerin intendiert“ (Verboom, 2004, 10) und nicht immer das, was didaktisch erwünscht wäre, gerade wenn sie noch ungeübt darin sind, Entdeckungen zu machen. Über das, was als Entdeckung und damit als Thema für den Austausch gelten soll, müssen sich die Lehrkraft und Schüler verständigen.
Natürlich gibt es „keine ‚richtigen‘ oder ‚falschen‘ Entdeckungen“ (ebd.), eine klare und problemorientierte Aufgabenstellung und transparente Erwartungshaltung der Lehrkraft sind aber hilfreich. Zusätzlich sollte die Lehrkraft versuchen, die Mathematik in der Antwort des Schülers zu betonen und in den Fokus zu rücken. Auf diese Weise kann der mathematische Blick geschärft und der mathematische Gehalt in Ideen und Äußerungen der Schülerinnen und Schüler erhöht werden. Dies wird zum einen durch eine „Haltung des ermunternden Zuhörens“ (Schütte, 2002, 16) gefördert, in der das authentische Interesse des Gesprächspartners an den individuellen Entdeckungen sichtbar ist.
Zum anderen ist eine Gesprächsführung hilfreich, die in den Mittelpunkt rückt, was das Kind schon kann und wo das Sinnhafte in seinen Äußerungen liegt und sich damit an den Kompetenzen des Kindes orientiert (vgl. Diagnose- und Fördergespräche / Diagnose- und Fördermomente). Trotzdem wird es Äußerungen geben, die keine mathematisch reichhaltigen Entdeckungen beinhalten. Auch dies muss von der Lehrkraft – wertschätzend und angemessen – deutlich gemacht werden, um den Lernenden die nötige Orientierung zu geben.
Entdeckungen, Ideen und Vorgehensweisen verständlich zu kommunizieren und dabei besonders den mathematischen Gehalt in den Fokus zu nehmen, müssen Kinder erst erlernen.
Die folgenden drei Handlungsfelder (vgl. Verboom, 2004; Korten, 2020) zeigen, welche Anforderungen die Lernenden dabei bewältigen müssen. Zu jedem Arbeitsfeld existieren auf Seiten der Lehrkraft unterschiedliche Möglichkeiten, individuelle Anpassungen vorzunehmen und Hilfestellungen zu leisten, um auf die individuellen Bedürfnisse und Lernvoraussetzungen der Schülerinnen und Schüler eingehen zu können.
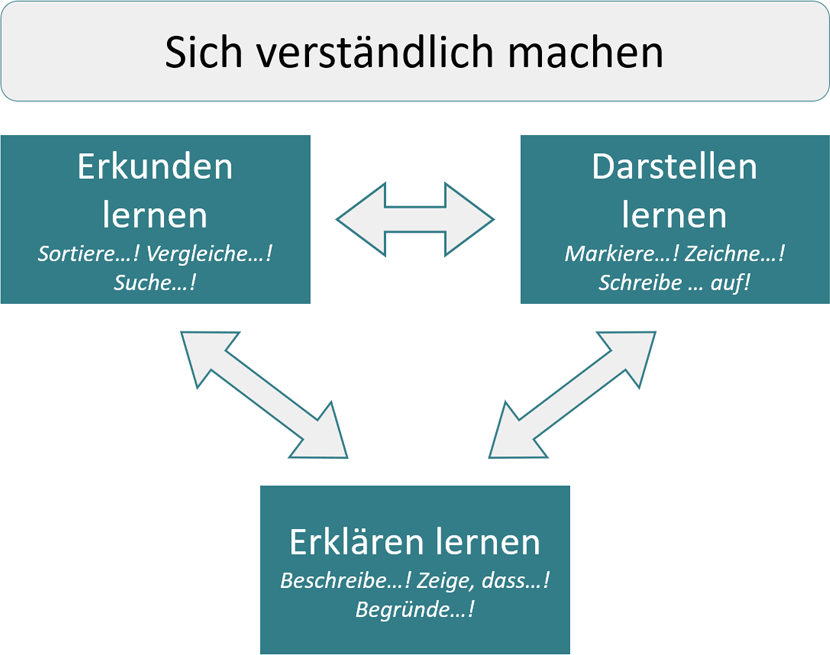 Abbildung 3 - Arbeitsfelder mit dem Ziel, verstanden zu werden
Abbildung 3 - Arbeitsfelder mit dem Ziel, verstanden zu werden
Die Schülerinnen und Schüler sollen beim Erkunden lernen, bei substantiellen Aufgabenformaten einen forschenden Blick einzusetzen, der es ihnen ermöglicht, mathematische Entdeckungen zu machen. Dabei kann es sich z.B. um Regelmäßigkeiten und Muster handeln oder um Lösungsstrategien und geschicktes Vorgehen.
Sie sollen dann, beim Darstellen lernen, diese Entdeckungen für sie selbst und andere sichtbar und (be-) greifbar zu machen, in dem sie z.B. Arbeitsergebnisse und Vorgehensweisen sortieren, systematisch notieren, markieren und beschreiben.
Im letzten Schritt sollen die Schülerinnen und Schüler beim Erklären lernen, wie man einem Gesprächspartner die eigenen Entdeckungen anhand seiner Arbeitsergebnisse und Aufzeichnungen verständlich machen kann.
Allen drei Handlungsfeldern gemein ist, dass sie von Schülerinnen und Schülern erlernt und sie dabei von der Lehrkraft unterstützt werden müssen. Dann kann davon ausgegangen werden, dass allen Lernenden Lern- und Entwicklungschancen in diesem Bereich eröffnet werden.
Weiterhin ist wichtig, dass die drei Handlungsfelder nicht getrennt voneinander „unterrichtet“ werden können und sollen, vielmehr bedingen sie sich gegenseitig. Gerade beim Erkunden und Darstellen handelt es sich um parallel ablaufende Vorgänge im Lernprozess der Kinder. Dem entsprechend sind auch Materialien oder Aufgabenstellungen nicht eindeutig einem der drei Handlungsfelder zuzuordnen. Die Trennung kann aber bei der differenzierten Planung von Unterrichtsvorhaben hilfreich sein.
Erkunden lernen
Obwohl durch substantielle Aufgabenformate „schnell Interesse geweckt und der (kindliche) Forscherdrang auch beim Umgang mit abstraktem ‚Zahlen-Material‘ aktiviert werden“ (Verboom, 2004, 7) kann, kommt es nicht selten vor, dass einzelne Kinder bei Aufgaben, die über das pure Ausrechnen hinausgehen, motivations- und orientierungslos erscheinen. Dafür kann es verschiedene Gründe geben.
Der Forscherblick
Häufig fehlt schlichtweg die Erfahrung, dass Mathematikunterricht mehr sein kann, als das korrekte Lösen von Rechenaufgaben. Gerade zu Beginn muss die Lehrkraft also vermehrt darauf achten, einem solchen Bild entgegenzuwirken und die Lernenden stetig durch Denkimpulse und Nachfragen zum „Forschen“ anregen. Symbole, wie Lupen o.ä., können eine sinnvolle Ergänzung hierzu darstellen, in dem sie Transparenz über das Aufgabenformat schaffen („Hier muss geforscht werden!“), bieten für sich aber keinen eigenen, ausreichenden Impuls zum Erkunden.
Umgang mit Offenheit
Eine zweite Hürde kann durch die Offenheit entstehen, die austauschanregende Aufgaben mit sich bringen. Dies kann gerade Kinder, die verinnerlicht haben, dass es im Mathematikunterricht nur „Richtig“ und „Falsch“ gibt, verunsichern (vgl. Verboom, 2004). Auch Kinder, die Probleme haben ihren Arbeitsprozess zu strukturieren oder generell eher ängstlich und unsicher sind, werden hier vor besondere Herausforderungen gestellt. Diese Hürde kann überwunden werden durch Strukturierungshilfen, gezieltes Nachfragen und Impulse sowie eine Grundhaltung der Lehrkraft, die ein unbefangenes Ausprobieren der Kinder begünstigt.
Rechnen kostet Energie
Drittens ist auch von Bedeutung, dass Kinder beim Erkunden nicht zu „viel Energie und Konzentration dafür aufbringen müssen […], die richtigen Rechenergebnisse zu ermitteln“ (Verboom, 2004, 9). Damit Kinder eine Problemstellung oder einen Aufgabenkomplex frei erkunden können, sollten sie sich im jeweiligen Zahlenraum sicher fühlen, wobei dieser meist durch eine natürliche Differenzierung freigestellt werden kann (vgl. ebd.). Es kann aber auch hilfreich sein, alle Ergebnisse schon vorzugeben, um den Fokus der Kinder auf die Aufgabenstruktur und weg vom Rechnen lenken, oder etwa Viertklässler bewusst im 20er-Raum rechnen zu lassen.
Insgesamt liegt die Herausforderung darin, den Blick der Lernenden für Zahlbeziehungen und differenzierte Lösungsstrategien zu schärfen, um sie so beim „Sehen“ von Entdeckungen zu unterstützen und das aktive Wahrnehmungsverhalten zu fördern (vgl. ebd.).
Im Folgenden wird die Herausforderung des Erkundens sowohl für Produkte als auch für Vorgehensweisen im Aufgabenformat der Zahlenmauer verdeutlicht.
´Erkunden´ von Produkten
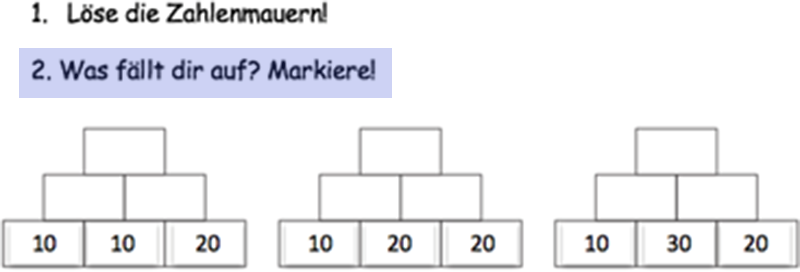 Abbildung 4 - Aufgabenstellung für den Austausch über Produkte
Abbildung 4 - Aufgabenstellung für den Austausch über Produkte
Die Lernenden können verschiedene Auffälligkeiten (die Konstanz der Außensteine, die konstante Erhöhung des Mittelsteines um 10 oder die Veränderung des Decksteins um je 20) finden. Nicht selten rechnen die Lernenden die Zahlenmauer im oben aufgeführten Beispiel hürdenfrei aus, die Zusammenhänge der Werte in der Zahlenmauer bleiben jedoch unentdeckt. Dann würde der Interaktionsprozess nicht zu einem ausgeglichenen Austausch über die erkundeten Muster, sondern vielmehr zu einem asymmetrischen Gespräch unter den Lernenden führen, in dem nur ein Partner erklärt und der andere zuhört. Natürlich soll es durch den Austausch auch möglich sein, dass Lernende sich gegenseitig unterstützen und voneinander lernen. Die Intention, seinen eigenen Ideen auf die Spur zu kommen, wird dabei jedoch verfehlt, hierfür muss jeder Lernende eigene Ideen – und seien sie auf den ersten Blick noch so klein und belanglos – entwickeln. Unterstützt werden können die Lernenden hier beispielsweise mit Schablonen, die die Aufmerksamkeit auf je einen Stein in allen Zahlenmauern lenken („Was soll verglichen werden?“) oder Vorgriffe aus dem Bereich Darstellen, wie Markierungen („Wo soll ich hinschauen?“) oder Pfeile („Was verändert sich?“).
´Erkunden´ von Vorgehensweisen
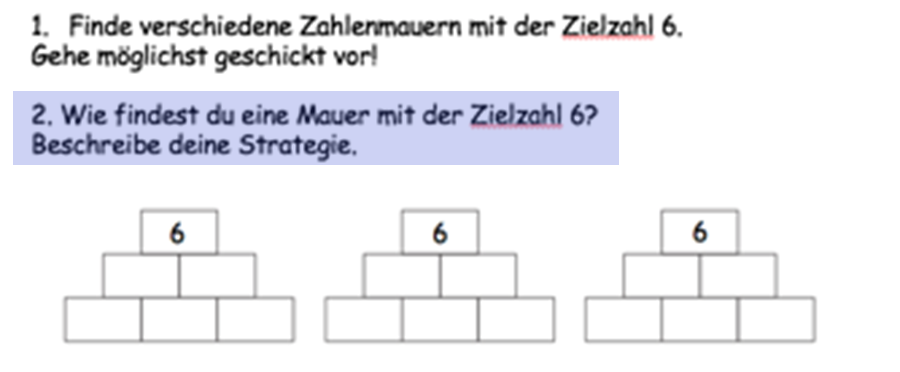 Abbildung 5 - Aufgabenstellung für den Austausch über Vorgehensweisen
Abbildung 5 - Aufgabenstellung für den Austausch über Vorgehensweisen
Die in Abbildung 5 dargestellte Aufgabe setzt den Schwerpunkt auf die Vorgehensweisen, mit denen die Lernenden die Zahlenmauern mit der Zielzahl 6 erreichen können. Die Aufforderung, rückblickend den Lösungsweg zu erkunden, stellt eine hohe kognitive Anforderung dar.
Häufig probieren die Lernenden zunächst unsystematisch, ehe sie Beziehungen für einen systematischen Lösungsweg nutzen. „Wenn Kinder noch ungeübt sind, sagen sie, sie hätten ´ganz normal´ oder ´im Kopf´ gerechnet. Meist läuft das Denken so schnell ab, dass es nicht fassbar wird.“ (Schütte, 2002, 17). Schütte verdeutlicht, dass die Lernenden dabei unterstützt werden müssen, ihre Lösungswege zunächst eigenständig zu erkunden, ehe diese im Austausch beschrieben werden können. Vorstrukturierte Dokumentationshilfen (Tabellen, Diagramme), Forschermittel (PIKAS: https://pikas.dzlm.de/node/556) oder auch Satzanfänge („erster Schritt: …, zweiter Schritt: …“) können die Lernenden dabei unterstützen, ihren Lösungsweg ins Bewusstsein zu rücken.
Darstellen lernen
Um Entdeckungen, Lösungsstrategien oder mathematische Inhalte im Allgemeinen darzustellen, können „Handlungen, bildliche Darstellungen [und] symbolische Darstellungen in der Umgangssprache oder in formaler Sprache“ (Kuhnke, 2011, 1) verwendet werden. Das „Darstellen lernen“ hat im Arbeitsprozess der Lernenden aus mehreren Gründen eine zentrale Rolle inne:
Entdeckungen sichtbar und begreifbar machen
Beim Darstellen werden Entdeckungen konkretisiert und damit bewusst gemacht. Die Beziehungen, Muster und Strukturen, die die Lernenden finden, ihr zunächst „unsichtbares“ mathematisches Wissen, müssen sie durch Darstellungen, Symbole und Zeichen sichtbar machen (vgl. Steenpaß, 2014). Diese „Übersetzungsleistung“ der Kinder kann eine große Herausforderung für sie darstellen und ist gleichzeitig ein grundsätzlicher Teil des Erkenntnisprozesses.
Unterschiedliche Darstellungsformen nutzen
Ein Unterricht, der einen gelingenden Austausch aller Lernenden zum Ziel hat, versucht mehrere Darstellungsmöglichkeiten anzubieten (siehe auch "Aufgaben adaptieren: Darstellungsmöglichkeiten" https://pikas-mi.dzlm.de/node/126 auf dieser Seite). Auf der einen Seite wird durch ein reiches Angebot von Darstellungsformen den unterschiedlichen Vorlieben, kognitiven Möglichkeiten und Kompetenzen der Lernenden entsprochen, auf der anderen Seite stellt der Wechsel zwischen Darstellungen eine elementare Fähigkeit im Mathematikunterricht dar, die beispielsweise „als Indikator für ein umfassendes Operationsverständnis“ (Kuhnke, 2011, 1) gilt.
Entdeckungen dokumentieren
Beim Darstellen werden Entdeckungen dokumentiert und damit für den mathematischen Dialog bereitgestellt. Vorbereitend auf die Phase des gemeinsamen Austauschs werden eigene Ideen von den Lernenden systematisch notiert, um damit eine sachbezogene Erklärung zu unterstützen, häufig sogar erst zu ermöglichen.
Auch hier wird im Folgenden die Herausforderung des Darstellens sowohl für Produkte als auch für Vorgehensweisen am Beispiel von Zahlenmauern verdeutlicht.
'Darstellen´ von Produkten
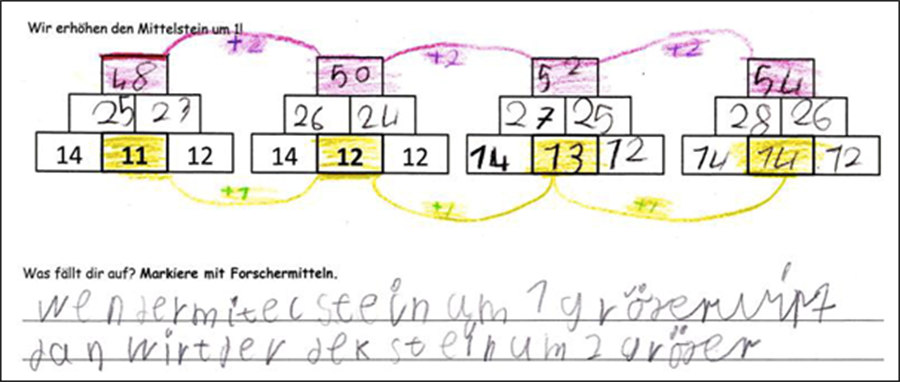 Abbildung 7 - Darstellen von Produkten
Abbildung 7 - Darstellen von Produkten
In diesem Beispiel wird gefordert, dass die Lernenden zunächst die Zahlenmauern erkunden („Was fällt dir auf?“) und ihre Entdeckungen darstellen sollen („Markiere mit Forschermitteln“). Die Darstellung von Auffälligkeiten, etwa konstante oder sich gleichmäßig verändernde Zahlen, als zentrale und herausfordernde Anforderung kann durch das Bereitstellen von Forschermitteln (Link zum Forscherplakat) unterstützt werden. Hier soll nun keine vollständige kompetenzorientierte Auswertung der Lernausgangslage vorgenommen werden, vielmehr werden kurz beispielhaft einige Entdeckungen aus dem Schülerdokument abgeleitet: Aus der Dokumentation wird deutlich, dass mehrere Entdeckungen gemacht wurden (gelb: der Mittelstein erhöht sich jeweils um 1; beide Ecksteine bleiben konstant; lila: der Zielstein erhöht sich jeweils um 2), die miteinander in Verbindung stehen und die auf unterschiedliche Weise markiert wurden (farbliche Codierung, Veränderungspfeile). Die Verbindung der gemachten Entdeckungen wurde außerdem schriftsprachlich durch eine wenn-dann-Formulierung ins Verhältnis gesetzt.
´Darstellen´ von Vorgehensweisen
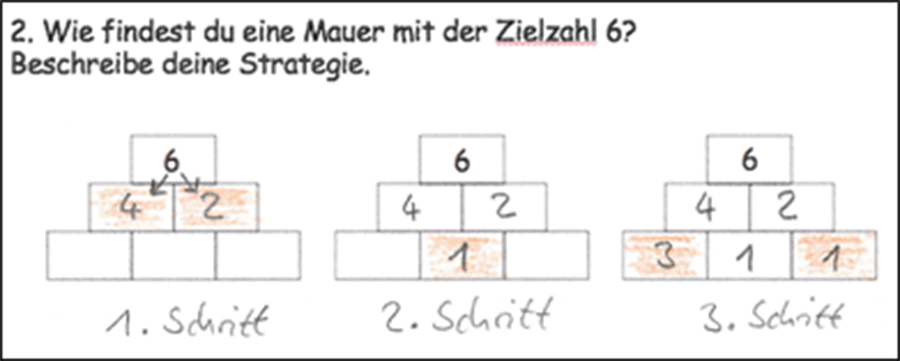 Abbildung 8 - Darstellen von Vorgehensweisen
Abbildung 8 - Darstellen von Vorgehensweisen
In diesem Beispiel wird von den Lernenden gefordert, ihre Lösungsstrategien bei der Problemlösung darzustellen. In der Abbildung stellt der Schüler seine Vorgehensweise anhand einer zeitlichen Abfolge von Schritten dar. Er markiert in jeder Zahlenmauer die neu ausgefüllten Steine und benutzt bspw. Pfeile, um auszudrücken, dass die „6“ im Deckstein zerlegt wird. Durch die Möglichkeit die einzelnen Lösungsschritte separat zu dokumentieren hat der Lernende die Chance, diese als Grundlage beim Beschreiben im Austausch zu nutzen. Bei mehreren Vorgehensweisen kann dann nach Unterschieden und Gemeinsamkeiten gesucht werden.
Erklären lernen
Hiermit ist der dialogische Austausch mit Interaktionspartnern gemeint, wobei der Fokus in diesem Teilmodul auf dem Sprecher und damit sowohl auf dem Ziel des „Verstanden Werdens“, als auch auf dem „für sich selbst Klären“ liegt. Die beim Erkunden und Darstellen gemachten Arbeitsschritte finden hier ihre Anwendung und werden im besten Fall gleichzeitig reflektiert. Das „Beschreiben müssen“ trägt dazu bei, eigene Ideen nochmals zu konkretisieren, zu vereinfachen und damit für sich selbst klären zu müssen. Die soziale Interaktion wirkt dabei als sinnstiftende Rahmung, austauschanregende Aufgabenformate (Link Eingangstext) bleiben jedoch Voraussetzung.
„Spielerisches“ Argumentieren
Wenn im Dialog eigene Ideen, Vorgehensweisen oder Vermutungen begründet werden sollen, wird „spielerisches“ mathematisches Argumentieren angeregt. Der Partner soll von der eigenen Begründung überzeugt werden, Vermutungen werden überprüft und im besten Fall verallgemeinert. Selbst wenn diese Prozesse nur rudimentär und in Ansätzen vollzogen werden, bilden sie doch eine wichtige und kindgerechte Übung des Argumentierens.
Eine gemeinsame Sprache finden
Häufig geht es im Dialog außerdem um das „Aushandeln von Bedeutungen“ (Bauersfeld, 2002, 12), wobei „erst die Kommunikation und Interaktion mit anderen dazu beiträgt, Verallgemeinerungen auch sozial zu akzeptieren, ihnen […] eine stabile Bedeutung zu geben“ (Steinbring, 1993, 117). Dabei entwickeln die Schülerinnen und Schüler eine gemeinsame Sprache – eine Sprache der Mathematik. Ein Ergebnis kann z.B. ein gemeinsamer Klassenwortschatz sein.
Die Lernenden sollten in diesem Teilmodul deshalb auch in der Entwicklung ihrer sprachlichen Fähigkeiten unterstützt werden. Sie müssen für die Beschreibung „ihrer Denkprozesse [und -produkte] eine Sprache finden, die zum tragfähigen Medium ihrer Denkbewegungen“ (Schütte, 2002, 17) wird.
Ein Klassenwortschatz oder ein themenbezogener Wortspeicher kann sie darin unterstützen. Ebenso wichtig ist aber die Möglichkeit, ihre Äußerungen auf verschiedenen Darstellungsebenen begleiten zu können, etwa handelnd, unter Zuhilfenahme von Anschauungsmaterial oder auf eigene ikonische oder symbolische Darstellungen verweisend. Gerade für das Argumentieren ist diese Möglichkeit von enormer Bedeutung.
‚Erklären‘ von Produkten
Ein Schüler (8 Jahre) erklärt seine Entdeckungen bei Zahlenmauern mit wachsendem Mittelstein.
Wie in den vorherigen Beispielen sollten die Lernenden zunächst Muster in den Zahlenmauern (die Grundreihe war vorgegeben) erkunden und ihre Entdeckungen mit Forschermitteln darstellen. Auch hier werden nur beispielhaft einige Aspekte aus der Schülerlösung herausgegriffen, um das Handlungsfeld „Erklären Lernen“ zu verdeutlichen. Die Markierungen im Video (blaue Kreise) zeigen, wann und wo der Schüler (8 Jahre) auf sein Dokument gezeigt hat. Insgesamt wird deutlich, dass er vor allem seine Aufzeichnungen nutzt, um Entdeckungen zu beschreiben, die er sprachlich nur mit wenigen Worten begleitet. In Verbindung mit den Markierungen, der schon vorher schriftlich formulierten Aussage „Immer zwei mehr…“ und seinen Ankündigungen „Hier habe ich entdeckt…“ kann er trotzdem zeigen, dass er einige Entdeckungen gemacht hat. Um den Schüler an dieser Stelle in seinen sprachlichen Fähigkeiten zu unterstützen, wäre beispielsweise ein auf das Aufgabenformat bezogener Wortspeicher, wie in Abbildung 10 hilfreich.
 Abbildung 10 - Wortspeicher Zahlenmauer
Abbildung 10 - Wortspeicher Zahlenmauer
Interessant ist zusätzlich, dass der Lernende unter die Zahlenmauern die Zahlen der 2. Reihe erneut aufgeschrieben und zahlreiche Regelmäßigkeiten (konstante Zehner, aufsteigende Einer und konstante Differenzen von „1“ zwischen dem linken und rechten Stein aufeinanderfolgender Zahlenmauern) umkreist hat, was seine Dialogpartnerin mit „Ich erkenn da überhaupt nix!“ kommentiert. Wie im Exkurs „Was sind eigentlich alles Entdeckungen?“ angemerkt, sehen Kinder oft viel mehr als intendiert. Hier können bei gleichbleibendem Format weitere Aufgaben- und Fragestellungen („Wächst der Deckstein auch bei anderen/ allen Zahlenmauern um 2, wenn sich der Mittelstein um 1 erhöht?“, „Finde Zahlenmauerfolgen, bei denen sich der Deckstein um 4 erhöht!“, „Warum kann sich der Deckstein nicht um 3 erhöhen?“) die Lernenden darin unterstützen, relevante Entdeckungen mit einander in Verbindung zu bringen oder zu verallgemeinern.
‚Erklären‘ von Vorgehensweisen
Eine Schülerin (9 Jahre) erklärt ihr Vorgehen bei Zahlenmauern mit dem Deckstein 60.
In diesem Beispiel sollte die Schülerin (9 Jahre) ihr Vorgehen beschreiben, wie sie verschiedene Zahlenmauern mit der „60“ im Deckstein gefunden hat. Im Gegensatz zum Schüler aus dem vorherigen Beispiel hat sie ganz auf Markierungen oder schriftlich vorformulierte Aussagen verzichtet und beschränkt sich auf ihre Lösungen. Auch hier wurde im Video markiert, wann und wo sie auf das Dokument gezeigt hat. Bereits zu Beginn erklärt sie, dass sie die erste Zahlenmauer zunächst nicht vollständig lösen konnte („wegen der ‚1‘ “) und deshalb eine zweite darunter geschrieben hat. Interessant ist, dass sie das genaue Problem erst (zum Ende des Videos) auf Nachfrage ihres Dialogpartners beschreibt. Mit ihrer Erklärung und der Aussage „Weil die ‚9‘ größer ist als die ‚1‘ “ bringt sie gleichzeitig einen Ansatz, den sie zu einer Regel für das Erstellen von Zahlenmauern weiterentwickeln könnte und den sie ohne ihren Partner vielleicht nicht formuliert hätte. Nachdem sie bei der zweiten Zahlenmauer von links die Zerlegung des Decksteins noch unsystematisch vornimmt und das auch so kommuniziert „das ist mir gerade so eingefallen“, geht sie bei der nächsten Zahlenmauer systematisch vor, in dem sie die zweite Zeile um „1“ erhöht, bzw. um „1“ vermindert, die vorherige Zerlegung also gegensinnig verändert.