Das hier vorgestellte Aufgabenformat zum Zerlegen von Geldbeträgen findet sich unter dem Titel „Lege anders!“ auch im Bereich ‚Inhalte‘: Größenvorstellungen und Umgang mit Größen (Geldwerte). Der mathematische Inhalt ist unter dem angegebenen Link für die Aufgabenstellungen in gewohnter Weise differenziert aufbereitet (Reduktion, Erweiterung und individuelle Unterstützung) und umfassend dargestellt.
Der Schwerpunkt in diesem Teilmodul liegt auf der exemplarischen Aufbereitung der Aufgabe hinsichtlich eines gemeinsamen Austausches der Lernenden. Dabei können sich die Lernenden über die Produkte ihrer Arbeit unterhalten („Was ist das Ergebnis meiner Arbeit?“) und über ihr Vorgehen („Wie bin ich zu meinem Ergebnis gekommen?“). Damit der Gegenstand des Austausches den Lernenden so deutlich wie möglich gemacht wird, werden hier zwei Aufgabenstellungen vorgestellt – eine zu den Produkten und eine zu den Vorgehensweisen der Kinder.
Um allen Kindern einen gelungenen Austausch zu ermöglichen, werden Maßnahmen dargestellt, die sie in den Arbeitsfeldern „Erkunden lernen“, „Darstellen lernen“ und „Erklären lernen“ unterstützen sollen.
Aufgabenstellung: Produkte
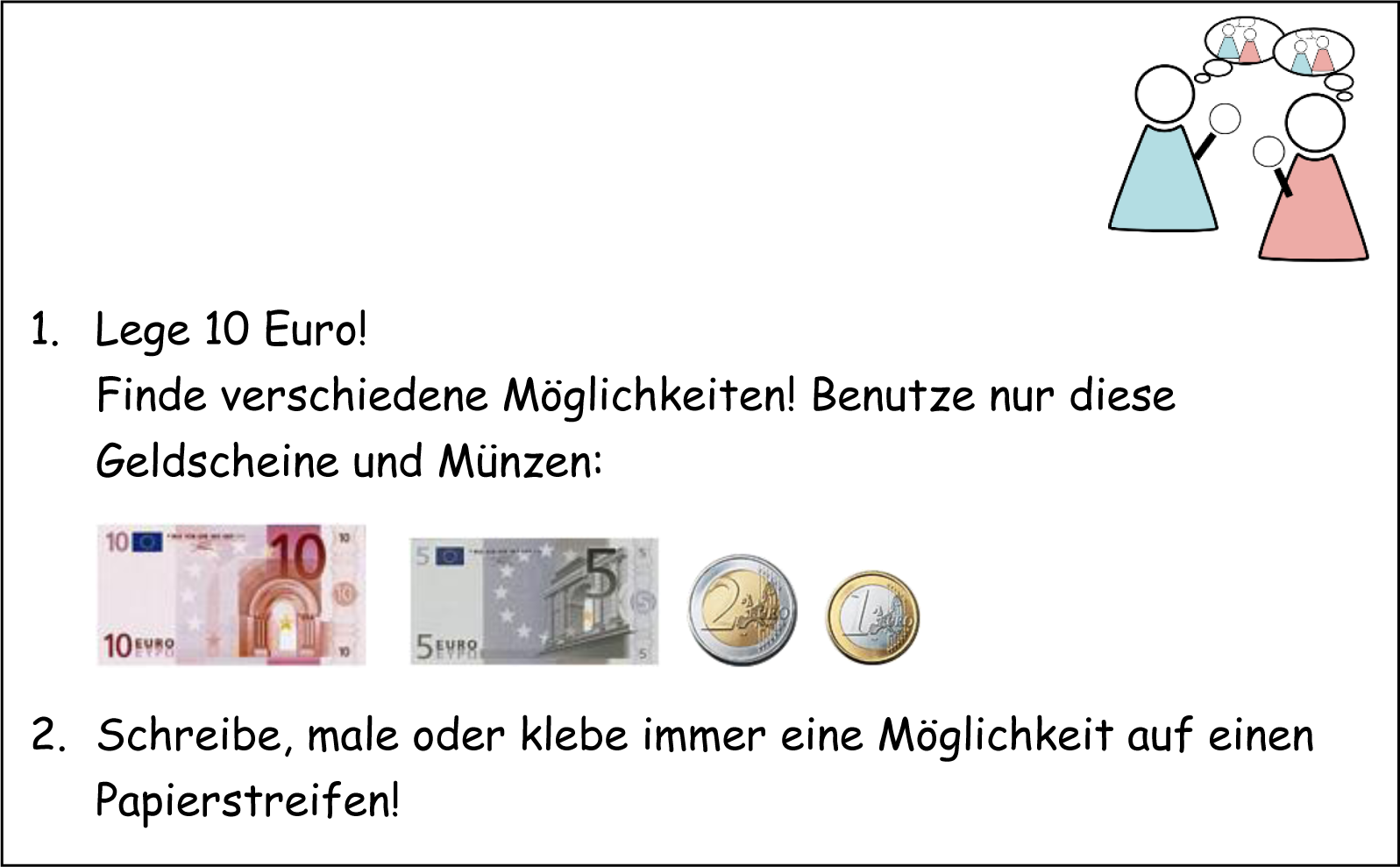 Abbildung 1 - Aufgabenstellung für das Erkunden und Darstellen von Produkten
Abbildung 1 - Aufgabenstellung für das Erkunden und Darstellen von Produkten
In der Vorbereitung auf den Austausch sollen die Lernenden zunächst unterschiedliche Möglichkeiten finden, 10€ mit den dargestellten Geldscheinen und -münzen zu legen und diese auf Papierstreifen zu schreiben, zu malen oder zu kleben. Die gefundenen Zerlegungen – ganz unterschiedlicher Art – sind das Arbeitsergebnis der Kinder und damit Gegenstand des Austausches.
Dabei lassen sich verschiedene Gesprächsanlässe ausmachen:
-
Vergleich der Anzahl der gefundenen Möglichkeiten
-
Vergleich der einzelnen Möglichkeiten (Welche sind gleich/ verschieden?)
-
Vergleich der gewählten Darstellungen (symbolisch / ikonisch etc.)
 Abbildung 2 - Lösungsmöglichkeiten der Aufgabenstellung zur Zerlegung der 10
Abbildung 2 - Lösungsmöglichkeiten der Aufgabenstellung zur Zerlegung der 10
Die hier abgebildeten Lösungsmöglichkeiten zeigen die Vielfalt möglicher Schülerprodukte. Diese Vielfalt an Produkten bietet nicht nur Gesprächsanlässe in der Phase des gemeinsamen Austausches. Zusätzlich ermöglicht die Offenheit der Aufgabe Kindern mit unterschiedlichen Lernvoraussetzungen eine erfolgreiche Bearbeitung, eine natürliche Differenzierung. Die gemeinsame Weiterarbeit mit den individuellen Arbeitsergebnissen begünstigt einen produktiven Umgang mit der Heterogenität der Klasse – die Verschiedenheit der Schülerprodukte wird als Mehrwehrt, als Chance begriffen.
 Abbildung 3 - Aufgabenstellung für den Austausch über Produkte
Abbildung 3 - Aufgabenstellung für den Austausch über Produkte
Im gemeinsamen Austausch haben die Lernenden die Aufgabe, sich ihre gefundenen Möglichkeiten gegenseitig vorzustellen. Außerdem sollen gleiche Möglichkeiten einander zugeordnet und diese Zuordnung im nächsten Schritt erklärt werden. Wann und warum es sich bei zwei Zerlegungen trotz unterschiedlicher Darstellungsformen oder Anordnungen der einzelnen Teile um dieselbe Möglichkeit handelt, ist somit mathematischer Inhalt des Austausches.
Aufgabenstellung: Vorgehensweisen
 Abbildung 4 - Aufgabenstellung für das Erkunden und Darstellen von Vorgehensweisen
Abbildung 4 - Aufgabenstellung für das Erkunden und Darstellen von Vorgehensweisen
Anders als in der vorangegangenen Aufgabe sollen die Lernenden hier alle Möglichkeiten finden, 10€ mit den vorgegebenen Geldscheinen und Münzen zu legen. Dabei darf jeder Geldschein und jede Münze beliebig oft genutzt werden. Zusätzlich sollen die Lernenden ihre gefundenen Möglichkeiten sortieren, um sicher sein zu können, alle Möglichkeiten gefunden zu haben.
Der Auftrag zu sortieren, erfüllt eine Doppelfunktion:
-
Zum einen können noch fehlende Zerlegungen einfacher entdeckt werden.
-
Zum anderen werden Lernenden darin unterstützt, nach Zusammenhängen zwischen ihren Zerlegungen zu suchen.
Die Fragen: „Wonach sortiere ich?“ „Womit fange ich an?“ „Wann geht es nicht mehr weiter?“ können dabei helfen. Zusätzlich sollen die Lernenden, z.B. mit Forschermitteln, markieren wie sie vorgegangen sind oder sortiert haben. Auch hiermit werden mehrere Ziele verfolgt:
-
Die Aufmerksamkeit der Schülerinnen und Schüler wird auf ihr Vorgehen, auf die Frage nach dem „Wie?“ gelenkt.
-
Das Markieren oder Nutzen von Forschermitteln kann helfen, Zusammenhänge zwischen Zerlegungen oder Kriterien für eine Sortierung zu finden oder bewusster werden zu lassen.
-
Diese bilden gleichzeitig die dokumentierte Grundlage für den gemeinsamen Austausch.
Was denken Sie? Wie viele Möglichkeiten gibt es insgesamt, und in welcher Reihenfolge würden Sie sie notieren?
Werden alle möglichen Zerlegungen der 10 nach den vorgegebenen Kriterien der Aufgabenstellung notiert, wird erkennbar, dass es
-
insgesamt 11 verschiedene Möglichkeiten der Zerlegung gibt,
-
und dass die Anordnung der Möglichkeiten nach unterschiedlichen Kriterien möglich ist.
Schauen Sie sich die verschiedenen Beispiele an. Können Sie erkennen, wie sortiert wurde?
Zerlegungen ohne Markierungen
 Abbildung 5 - Möglichkeiten der Sortierung aller Zerlegungen der 10
Abbildung 5 - Möglichkeiten der Sortierung aller Zerlegungen der 10
Zerlegungen mit Markierungen
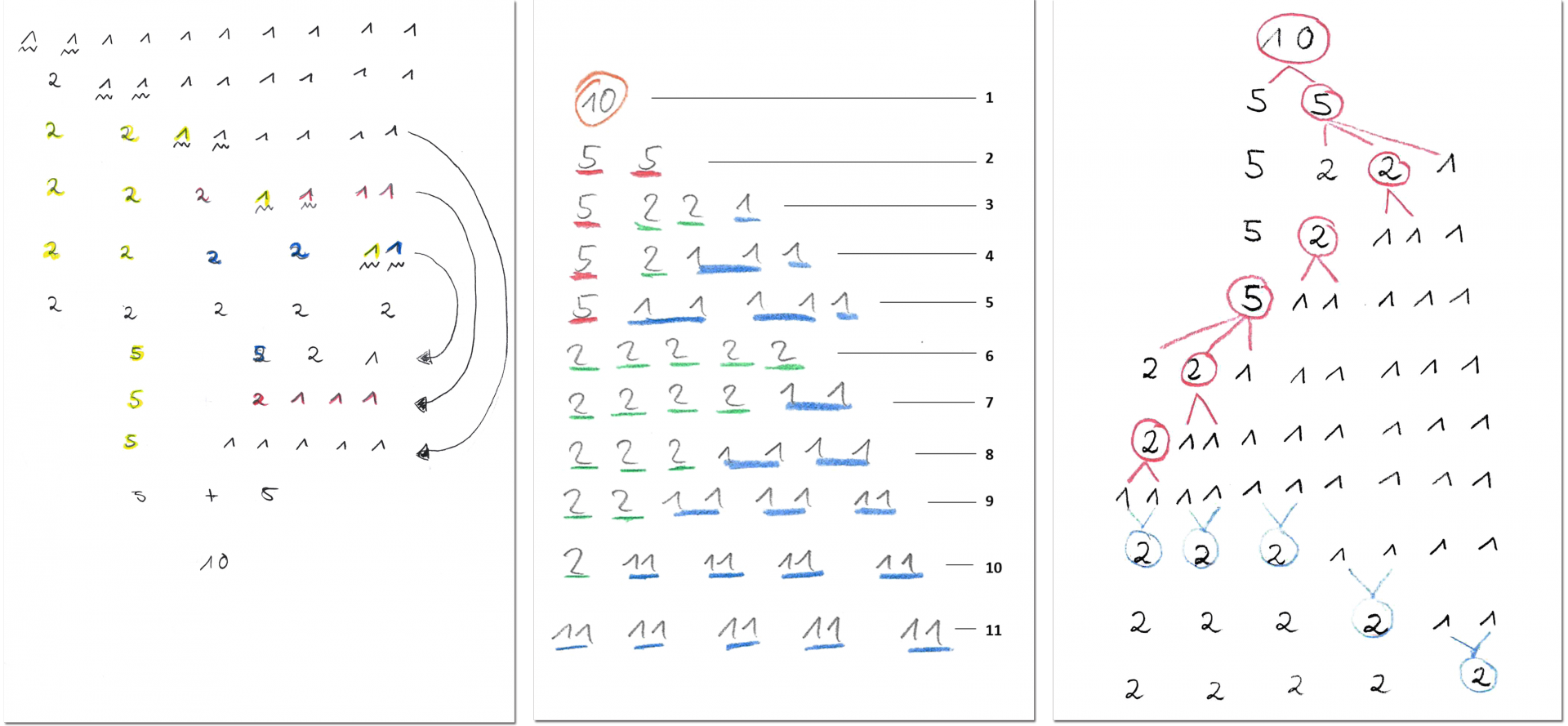 Abbildung 6 - Möglichkeiten der Sortierung aller Zerlegungen der 10
Abbildung 6 - Möglichkeiten der Sortierung aller Zerlegungen der 10
Die Abbildungen 5 und 6 zeigen verschiedene Möglichkeiten, alle Zahlzerlegungen nach verschiedenen Kriterien zu sortieren. Mit Hilfe farblicher Markierungen sollen die Ordnungsschritte verdeutlicht werden. Beispielsweise wurde in der Abbildung in der Mitte beim Sortieren darauf geachtet, schrittweise einen Geldschein oder eine Münze mehr zu zerlegen, so dass von Zeile zu Zeile die Anzahl an Geldscheine bzw. Münzen kontinuierlich steigt. Eine Ausnahme bildet Zeile 6, in der nur 2€-Münzen genutzt wurden, die dann ab Zeile 7 wieder systematisch zerlegt wurden.
In den abgebildeten Beispielen (vgl. Abbildung 6) wurden Farben und Pfeile verwendet, um das Vorgehen beim Sortieren oder Erstellen neuer Zerlegungen schriftlich anzudeuten. Es zeigt sich, dass es ohne zusätzliche Markierungen deutlich schwerer fällt, zu verstehen wie sortiert wurde. Schnell werden darüber hinaus Vor- und Nachteile verschiedener Darstellungsformen deutlich.
Im Unterricht ist davon auszugehen, dass nicht alle Schüler alle 11 möglichen Zerlegungen finden. Hier sollte, je nach Leistungsstand, überprüft werden, ob zunächst die Zerlegung von 5€ oder 7€ sinnvoller sein könnte, da analog zu dieser Aufgabe auch mit kleineren Zahlen dieselben Erkenntnisse („Wie zerlege ich systematisch?“) möglich sind. Gleichzeitig bieten gerade unvollständige Lösungen zahlreiche Lernchancen und Gesprächsanlässe in der Phase des Austausches – so können beispielsweise alle Möglichkeiten auch gemeinsam mit dem Partner gefunden werden.
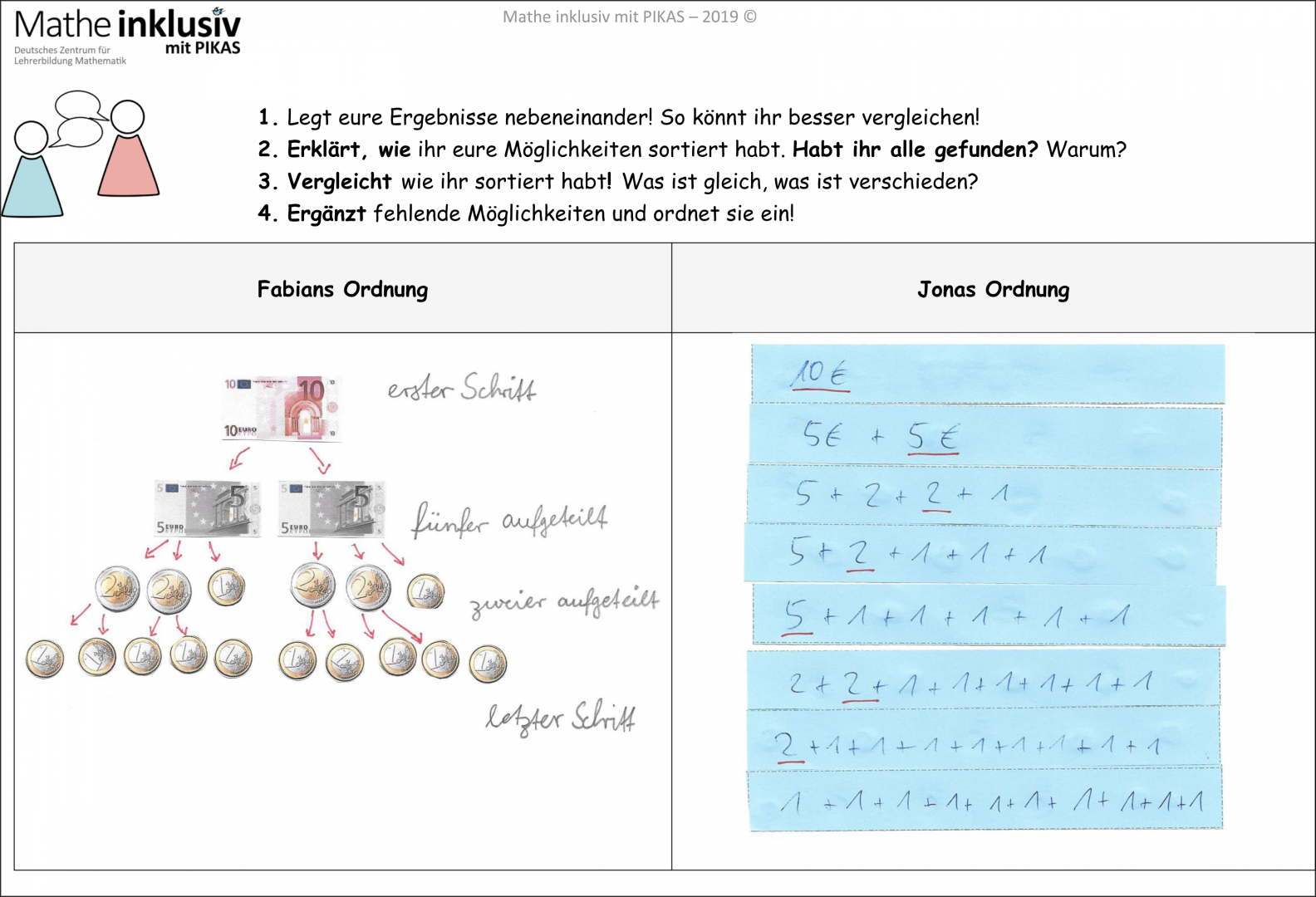 Abbildung 7 - Aufgabenstellung mit möglichen Lösungen für den Austausch über Vorgehensweisen
Abbildung 7 - Aufgabenstellung mit möglichen Lösungen für den Austausch über Vorgehensweisen
Im Arbeitsauftrag für die Austauschphase sollen die Lernenden ihrem Partner erklären, wie sie beim Sortieren der gefundenen Zerlegungen vorgegangen sind. Zusätzlich sollen sie begründen, warum sie alle Möglichkeiten der Zerlegung gefunden haben. In den Lösungen von Jonas und Fabian sieht man, dass sie Markierungen verwendet haben, um ihr Vorgehen zu verdeutlichen, auf die sie jetzt beim Erklären zurückgreifen können.
Die Arbeitsaufträge 3 und 4 erweitern und vertiefen die Auseinandersetzung mit den Arbeitsergebnissen. Sie bieten die Möglichkeit, gemeinsam an unvollständigen Lösungen weiter zu arbeiten oder das eigene Vorgehen zu reflektieren. Arbeitsaufträge, die das Nachdenken über die Lösungen des Gesprächspartners anregen, finden sich ausführlicher im Teilmodul „Andere verstehen“. Dennoch wird bereits an dieser Stelle deutlich, dass durch den gemeinsamen Austausch eigene Arbeitsergebnisse und Erkenntnisse weiterentwickelt werden können.
Unterstützungsmaßnahmen
Beide Aufgabenstellungen halten für die Schülerinnen und Schüler in den drei Handlungsfeldern „Erkunden lernen“, „Darstellen lernen“ und „Erklären lernen“ Herausforderungen bereit. Da sich die Handlungsfelder gegenseitig bedingen, sich nicht immer klar voneinander abgrenzen lassen und im Unterricht zum Teil zeitlich parallel ablaufen, sind die hier dargestellten Unterstützungsmaßnahmen nicht nach den Arbeitsfeldern sortiert aufgelistet, sondern in inhaltlich zusammenhängende Bereiche gegliedert, in denen sie kurz allgemein beschrieben und dann jeweils für die zugehörigen Handlungsfelder exemplarisch konkretisiert werden.
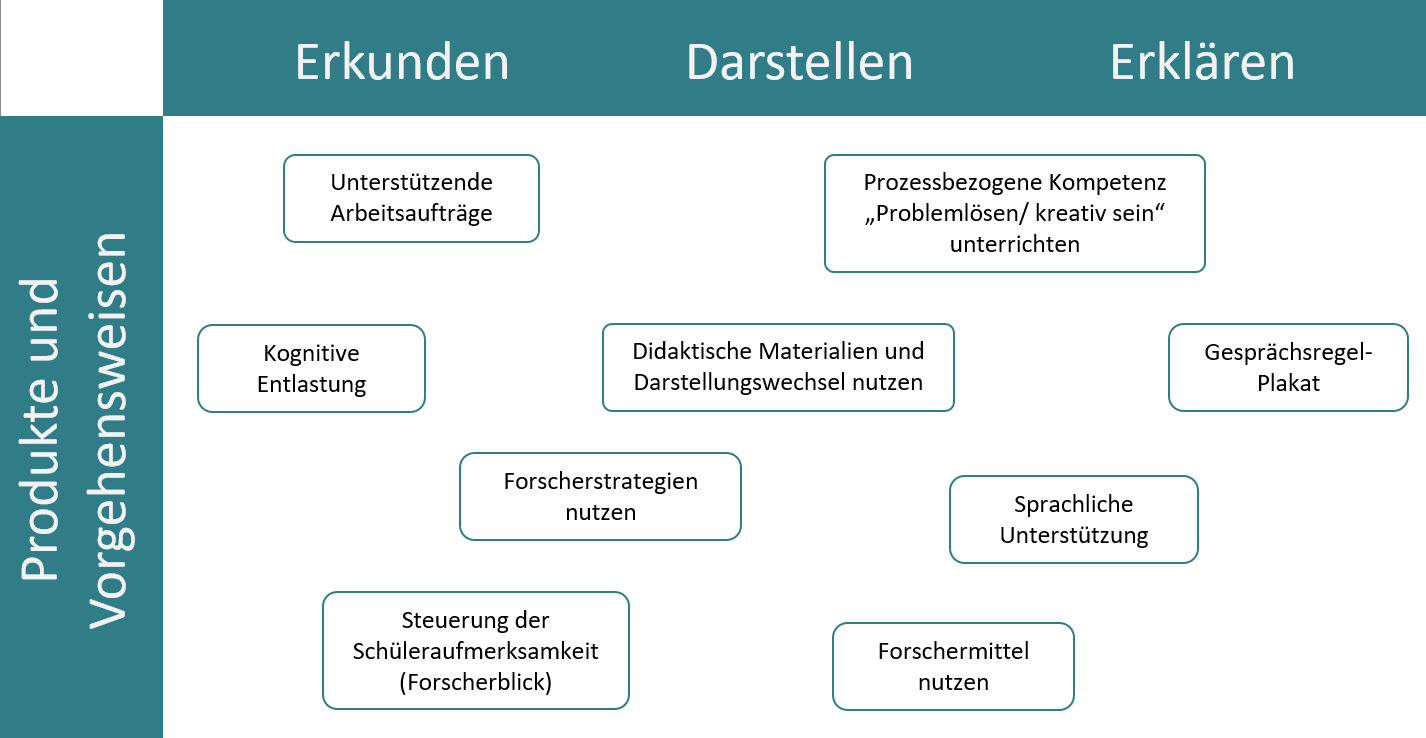 Abbildung 8 - Übersicht Unterstützungsmaßnahmen
Abbildung 8 - Übersicht Unterstützungsmaßnahmen
Unterstützende Arbeitsaufträge
Die Basisaufgabe beider offenen Aufgabenstellungen „Lege 10€. Finde viele/ alle Möglichkeiten!“ ist problemorientiert. Welche Lösungsstrategie und Darstellungsform der Möglichkeiten die Kinder wählen, kann individuell bestimmt werden. Die dadurch hergestellte natürliche Differenzierung ermöglicht allen Lernenden, anknüpfend an die individuellen Lernvoraussetzungen, ein Arbeiten am gemeinsamen Gegenstand. Die Offenheit der Aufgabenstellung kann vereinzelt eine Herausforderung darstellen. Besonders Kinder, die Schwierigkeiten haben, ihren Arbeitsprozess zu strukturieren, unsichere oder ängstliche Kinder benötigen hier Unterstützung.
Eine Möglichkeit, darauf einzugehen, bietet bereits die Aufgabenstellung. Die weiterführenden Arbeitsaufträge „Schreibe immer eine Möglichkeit auf einen Papierstreifen!“ und „Sortiere deine Möglichkeiten!“ bilden bereits wichtige unterstützende Handlungsschritte auf dem Weg zu einer Zerlegungsmöglichkeit. Sie unterstützen die Lernenden, indem sie
-
nacheinander ausführbar sind (es müssen nicht sofort alle Möglichkeiten gefunden werden),
-
die Zwischenergebnisse (hier die Möglichkeiten) erweiterbar bleiben (es können Streifen hinzugefügt werden),
-
das Endergebnis (die Reihenfolge) einfach zu manipulieren ist (die Streifen können händisch beliebig oft angeordnet werden),
-
es keine „richtige“ oder „falsche“ Reihenfolge gibt – Offenheit darüber besteht, wie die einzelnen Möglichkeiten angeordnet werden können.
Die Lernenden bekommen konkrete Arbeitsaufträge, die sie auf ihrem Lösungsweg unterstützen, die sie aber in ihrem mathematischen Handeln nicht einschränken – sie bleiben flexibel.
Der Forscherblick
Dass Mathematikunterricht mehr sein kann, als das korrekte Lösen von Rechenaufgaben, müssen viele Schülerinnen und Schüler noch lernen. Gerade wenn ihnen die Erfahrung zum Erkunden von Mustern, Strukturen oder Lösungswegen noch fehlt, bleibt unbekannt, wonach sie suchen sollen, es fehlt der „Forscherblick“. Grundsätzliche Voraussetzungen sind unter anderem:
-
eine angstfreie Arbeitsatmosphäre, in der die Lernenden sich trauen, am mathematischen Inhalt zu „forschen“ und die von der Lehrkraft durch ermutigende Kommunikation und den reflektierten Umgang mit Schülerbeiträgen unterstützt werden sollte
-
eine klare Zieltransparenz, beispielsweise hergestellt durch Impulse oder Arbeitsaufträge, aber auch durch Symbole (Lupen oder ähnliches), die den Lernenden verdeutlichen: „Bei dieser Aufgabe handelt es sich um eine Forscheraufgabe!“
In der Aufgabenstellung in Abbildung 4 werden die Lernenden bspw. aufgefordert, ihre Zerlegungsmöglichkeiten zu sortieren. Dies setzt voraus, dass die Lernenden Zusammenhänge zwischen den Zerlegungen erkunden und zusammenhängende Zerlegungen gefunden haben. Die Maßnahmen "Lösungsansätze vorgeben", "Beobachtungsaufträge erteilen" und "Informationen reduzieren" zeigen exemplarisch, wie Lernende, die hier Schwierigkeiten haben, unterstützt werden können.
Lösungsansätze vorgeben
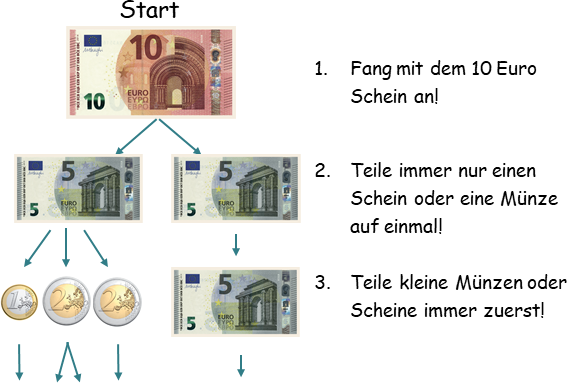 Abbildung 9 - Lösungsansätze vorgeben
Abbildung 9 - Lösungsansätze vorgeben
Erarbeiten die Schülerinnen und Schüler systematisch neue Zerlegungen, kann davon ausgegangen werden, dass sich das Sortieren als wenig problematisch herausstellt. Erarbeiten sich die Lernenden die Zerlegungen jedoch unsystematisch, ist zu beachten, dass wenig zusammenhängende Zerlegungen gefunden werden, wodurch das Sortieren deutlich schwerer wird. An dieser Stelle kann es sinnvoll sein, Zerlegungsmöglichkeiten vorzugeben, indem „Schülerlösungen“ eingebracht werden, die es nachzuvollziehen gilt: „Dieser Schüler hat seine Entdeckung mit Forschermitteln markiert! Was hat er entdeckt?“ Denkbar ist auch alle Möglichkeiten, 10€ zu legen, vorzugegeben, mit dem Arbeitsauftrag: „Sortiere die Möglichkeiten und überprüfe, ob es noch mehr geben kann! Markiere, wie du sortiert hast!“
Beobachtungsaufträge erteilen
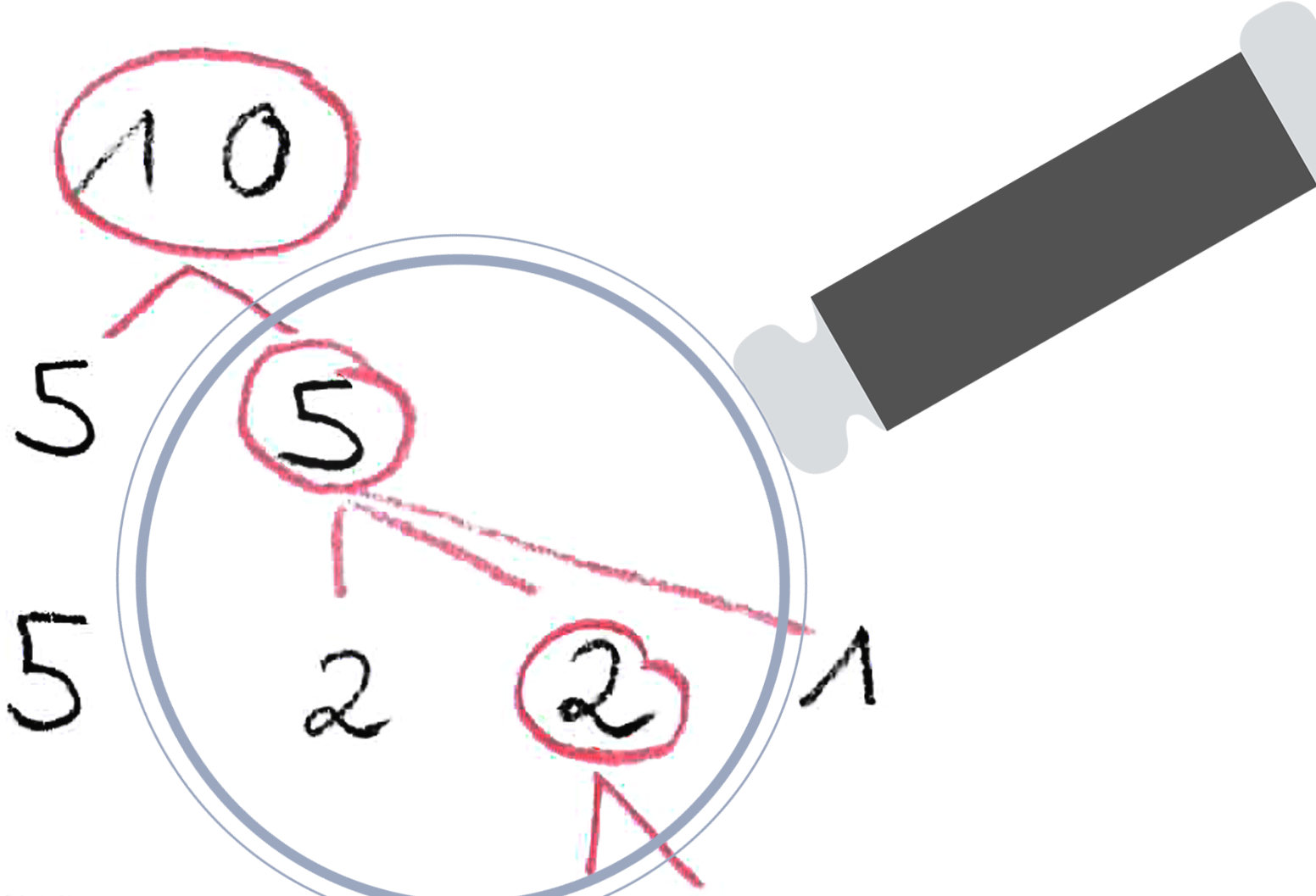 Abbildung 10 - Beobachtungsauftrag
Abbildung 10 - Beobachtungsauftrag
Beobachtungsaufträge, wie „Was hat sich hier von Möglichkeit 1 zu Möglichkeit 2 verändert?“, „Was bleibt bei den ersten fünf Möglichkeiten gleich?“ können die Lernenden darin unterstützen bestimmte Ausschnitte eines Inhaltes in den Fokus zu nehmen. Ähnliches kann auch nonverbal, etwa durch Lupensymbole, wie in der Abbildung gezeigt, erreicht werden und signalisiert dem Lernenden „Schau hier genauer hin!“. Auch Forschermittel stellen eine gute Möglichkeit dar, die Aufmerksamkeit der Schüler auf bestimmte Sachverhalte zu lenken.
Informationen reduzieren
Die Reduktion von Informationen, etwa durch den Einsatz von Schablonen, die über die Aufgabenstellung oder Lösung gelegt wird, ist eine weitere Möglichkeit, Schüleraufmerksamkeit zu lenken. Sie ist deshalb von großer Bedeutung, weil sie eine Reizreduktion darstellt, wodurch Kinder mit Wahrnehmungsproblemen profitieren. Hier könnte zum Beispiel einfach ein weißes Blatt genutzt werden, dass über die gefundenen Zerlegungen gelegt wird und so zunächst alle ersten Summanden der Zerlegungen gezeigt werden, dann alle zweiten Summanden usw..
Die Prozessbezogene Kompetenz „Problemlösen/ kreativ sein“ zum Thema machen
Grundsätzlich ist es von Bedeutung, im Unterricht den Umgang mit Offenheit und problemorientierten Aufgaben zu thematisieren und den Schülerinnen und Schülern generell Lernchancen im Bereich der prozessbezogenen Kompetenzen „Problemlösen / kreativ sein“ (vgl. Zannetin & Selter, 2018, 9ff.) zu ermöglichen. Wie dies gelingen kann, wird beispielsweise im Infopapier „Das nutzen Matheforscher“ bei PIKAS anschaulich umrissen. Dort werden unter anderem „Forscher-Schritte“ und „Forscher-Strategien“ für Kinder in der Grundschule formuliert, die – transparent und kindgerecht – als Lernplakat im Klassenraum zugänglich gemacht werden.
PIKAS: Matheforscher-PlakatPIKAS: Infopapier "Das nutzen Matheforscher"
Forscherstrategien nutzen
Die bei PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Informationsmaterial – Plakate vorgestellten Forscherstrategien können je nach Aufgabenformat konkretisiert und adaptiert werden und zwar sowohl von den Schülerinnen und Schülern als Teil der Aufgabe als auch im Vorfeld von der Lehrkraft als zusätzliche Unterstützungsmaßnahme. Bezogen auf die Aufgabenstellung zu den Vorgehensweisen hieße das für das „geschickte Probieren“ z.B.: „Versuche aus einer Möglichkeit eine neue zu machen, indem du nur einen Geldschein oder ein Geldstück neu zerlegst. Für eine weitere Möglichkeit, zerlege wieder nur einen Geldschein oder ein Geldstück. Mache immer so weiter, bis …?“. Auch das „rückwärts denken“ lässt sich als Strategie anpassen: „Beginne mit zehn 1€-Stücken und fasse dann zwei von ihnen zu einem 2€-Stück zusammen! Fasse Schritt für Schritt weiter zusammen, um alle Möglichkeiten zu finden!“. Je mehr Forscherstrategien die Lernenden aus anderen Aufgabenformaten kennen, desto eher werden sie passende Vorgehensweisen für dieses Problem entdecken.
Der Einsatz von Forscherstrategien unterstützt die Lernenden somit zum einen bei der systematischeren Lösung einer Problemlöseaufgabe. Zentral werden damit die Herausforderungen des Erkundens und Erklärens angesprochen. Das Erkunden wird dadurch erleichtert, dass den Lernenden Strategien angeboten werden, eine Aufgabe systematisch zu bearbeiten. Vorteile im Bereich des Erklärens bildet im Anschluss die Möglichkeit, dass die Lernenden ihr Vorgehen mit einer Strategie konkret benennen und dann anhand ihres Beispiels beschreiben können.
Kognitive Entlastung
Wie auch im Hintergrundteil zum Thema Erkunden lernen dargestellt, kann es für Kinder schwer werden, die für das Problemlösen notwendige Flexibilität und Kreativität aufzubringen, wenn ihnen das korrekte Ermitteln von Rechenergebnissen (hier: das rechnerisch korrekte Zerlegen der „10“) zu viel Energie und Konzentration abverlangt (vgl. Verboom, 2004) – von der Motivation ganz zu schweigen. Aus diesem Grund sollte immer überprüft werden, ob es sinnvoll sein könnte, die Kinder kognitiv zu entlasten.
Lernende können auf zahlreichen Wegen kognitiv entlastet werden, von denen im Folgenden die Anpassung des Zahlenraumes und der Einsatz digitaler Medien exemplarisch aufgegriffen werden ohne dabei Anspruch auf Vollständigkeit zu gewähren.
Anpassung des Zahlenraums
Sowohl in der Aufgabenstellung zu den Produkten als auch zu den Vorgehensweisen müssen die Lernenden die Menge 10 zerlegen. Die Fertigkeit der Zahlzerlegung setzt voraus, dass die Lernenden ein Verständnis über die Menge von Zahlen (das kardinale Zahlverständnis) bereits entwickelt haben und wissen, dass eine Menge aus Teilen zusammengesetzt werden kann.
Eine Möglichkeit der kognitiven Entlastung bietet hier die Anpassung des Zahlenraums. Wird in der Basisaufgabe die Zerlegung der 10 verlangt, besteht die Möglichkeit, dass einzelne Lernende – je nach Bedarf – den Zahlenraum verkleinern. Der Arbeitsauftrag „Zerlege 5€. Finde alle Möglichkeiten!“ würde die Anzahl der Zerlegungsmöglichkeiten auf vier reduzieren und die Aufgabenstellung dadurch vereinfachen. In diesem Beispiel bildet die Veränderung des Zahlenraums keine Einschränkungen für den Austausch, da die 5 als Teil der 10 ebenso zerlegt werden kann. Außerdem kann die Anzahl der zu nutzenden Geldscheine und Münzen angepasst werden: „Lege 10€. Finde viele Möglichkeiten. Nutze nur 2€- und 1€-Münzen!“.
Besonderen Mehrwert für den Austausch bildet hier die Möglichkeit, dass die Lernenden überprüfen können, ob sich die Anzahl der Zerlegungen auch mit der Halbierung der Gesamtmenge halbiert.
Digitale Hilfsmittel zur Verfügung stellen
Eine weitere Möglichkeit der kognitiven Entlastung bei Unsicherheiten der Mengenzerlegung bildet der Einsatz von Taschenrechnern. Damit haben die Lernenden zum einen die Möglichkeit einzelne Zerlegungen zu finden oder aber auch gefundene Zerlegungen zu überprüfen. Der Einsatz des Taschenrechners setzt an dieser Stelle einen sicheren Umgang mit diesem voraus. Darüber hinaus gilt es zu reflektieren, dass sich das Ziel der Aufgabe auf das Finden einer Reihenfolge als prozessbezogene Kompetenz verlagert, sodass die Förderung der Zahlzerlegung in den Hintergrund rückt und der Lernende sich ganz auf die Begründung von mathematischen Entdeckungen konzentrieren kann.
Einbezug didaktischer Materialien und Darstellungswechsel
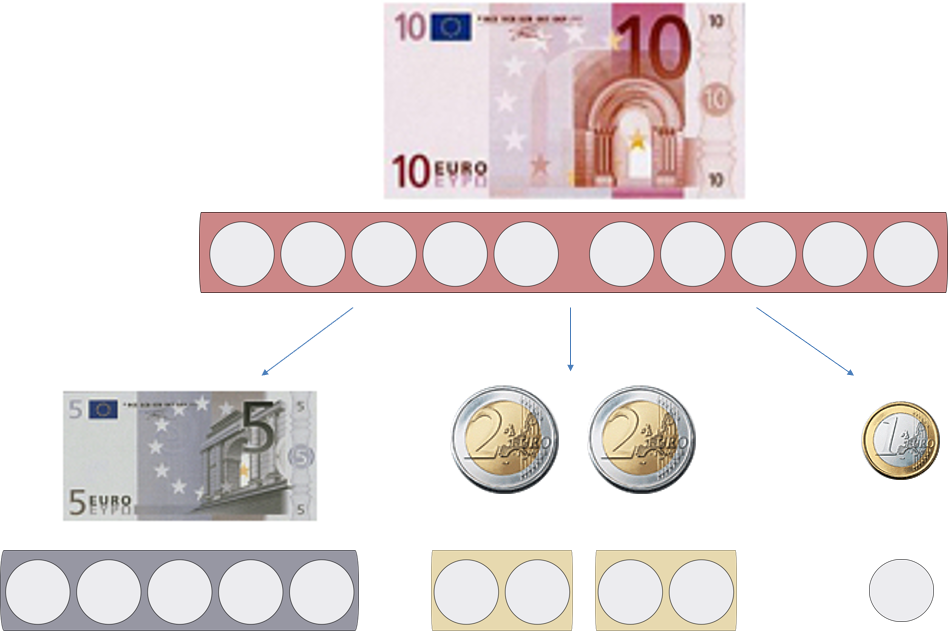 Abbildung 12 - Einbezug von Punktestreifen zur enaktiven Zerlegung einer Menge
Abbildung 12 - Einbezug von Punktestreifen zur enaktiven Zerlegung einer Menge
Die inhaltsbezogene Herausforderung der Zahlzerlegung kann ebenso mit Hilfe geeigneter didaktischer Materialien unterstützt werden. Dabei ist vorstellbar, dass der Einsatz von Punktestreifen die Lernenden bei der Zerlegung einer Menge unterstützen. Diese bieten den Vorteil, dass die auf Scheinen und Münzen nur symbolisch dargestellten Zahlen eine ikonische Entsprechung der Mengen bekommen. Das korrekte Herstellen von Zerlegungen der „10“ kann dann auch auf enaktivem Weg durchgeführt werden.
Der Einsatz didaktischer Materialien bietet an dieser Stelle demnach die Möglichkeit, verschiedene Zerlegungen einer Menge zu finden und Erkundungen zu diesen Zerlegungen anstellen zu können. Außerdem können sie hilfreich für die Herausforderung des Darstellens und des Erklärens sein.
 Abbildung 13 - Darstellung der gefundenen Zerlegungen mit unterschiedlichen Darstellungsformen
Abbildung 13 - Darstellung der gefundenen Zerlegungen mit unterschiedlichen Darstellungsformen
Der Einbezug enaktiv nutzbarer Materialien bringt ein besonderes Potenzial im Bereich des Erklärens mit sich. Vorgehensweisen und Überlegungen können mit Hilfe des Materials präsentiert werden. Besonders, wenn am Material zahlreiche Operationen durchgeführt wurden, können diese Vorgehen mit dem Material wiederholt werden, um dem Austauschpartner das Nachvollziehen zu erleichtern. Im Gegensatz zu statisch-schriftlichen Dokumentationen (Notizen, Pfeile, Farbmarkierungen), die ihren eigenen Wert und Nutzen haben, haben enaktive Darstellungsmittel den Vorteil, dass sie flexibel bleiben.
Besonders für die Herausforderung des Erklärens, sowohl von Produkten als auch von Prozessen ist der Wechsel der Darstellungsformen als unterstützende Maßnahme hervorzuheben. Dabei ist denkbar, dass Lernende zunächst auf ihre persönliche Darstellungsform zurückgreifen und diese im Austausch in eine andere Darstellungsform übersetzen. Dies setzt voraus, dass die Grundvorstellung dementsprechend entwickelt ist. Im unten aufgeführten Beispiel (vgl. Abbildung 14) werden die symbolisch dargestellten Zerlegungen zur besseren Nachvollziehbarkeit mit Hilfe des Materials gelegt, um den Austauschpartnern einen weiteren Zugang zur eigenen Lösung zu schaffen. Das Beispiel steht an dieser Stelle exemplarisch für den Darstellungswechsel zwischen der symbolischen und enaktiven Darstellungsform. Alle weiteren Übersetzungen in andere Formen sind selbstverständlich denkbar.
 Abbildung 14 - Übersetzung der symbolischen in die enaktive Darstellungsform
Abbildung 14 - Übersetzung der symbolischen in die enaktive Darstellungsform
Der Wechsel zwischen verschiedenen Ebenen der Darstellungen (enaktiv, ikonisch, symbolisch) kann darüber hinaus viele Lernchancen für die Lernenden bereithalten (Kuhnke, 2011, 1; PIKAS: Haus 3: Rechenschwierigkeiten – Unterrichtsmaterial – Guter Umgang mit Darstellungsmitteln). Beispielsweise kann im Austausch angeregt werden, die Darstellungsformen zu bewerten, oder durch einen Vergleich können Vor- und Nachteile erarbeitet werden.
Forschermittel
Der Einsatz von Forschermitteln und ihr Nutzen auf vielfältigen Ebenen ist im Hintergrund dieses Textes schon mehrfach angesprochen worden, etwa in ihrer Doppelfunktion beim Erkunden (die Kinder markieren, was ihnen auffällt und lenken dabei ihre Aufmerksamkeit auf diese Auffälligkeiten) und beim Darstellen (die Kinder dokumentieren diese Auffälligkeiten, um später beim Erklären darauf zurückgreifen zu können).
Forschermittel gehören, wie die Forscher-Schritte und Forscher-Strategien, zu den Hilfsmitteln im Problemlöseprozess und werden wie diese im Infopapier „Das nutzen Mathe-Forscher“ bei PIKAS kurz umrissen. Auf dem PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichtsmaterial – Forschermittelplakat sind die wichtigsten Forschermittel gesammelt und kurz erklärt, es eignet sich somit als Überblick und Erinnerungsstütze für die Schülerinnen und Schüler im Klassenraum.
Insgesamt muss beim Einsatz von Forschermitteln im Unterricht darauf geachtet werden, dass diese angemessen eingeführt und unterrichtet werden: Die Lernenden müssen wissen, wozu und wie sie genutzt werden können. Dazu genügt es nicht, einfach das Forschermittelplakat in der Klasse aufzuhängen, es sollte, ähnlich wie bei der Erstellung eines Klassenwortschatzes, gemeinsam mit der Klasse Schritt für Schritt, erweitert und vervollständigt werden.
Bezogen auf dieses Aufgabenformat sind nun einige Forschermittel exemplarisch als unterstützende Maßnahmen dargestellt.
Farbmarkierungen
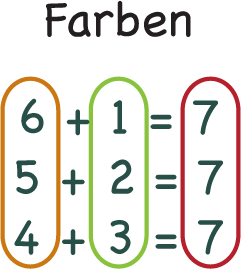 Abbildung 16 - Farbmarkierungen
Abbildung 16 - Farbmarkierungen
Farbmarkierungen eignen sich besonders gut dafür, die Aufmerksamkeit auf bestimmte Bereiche einer Darstellung zu lenken. Gerade wenn es sich um mehrere „Sammlungen“ von Zahlen, Elementen usw. handelt, sind Markierungen in verschiedenen Farben hilfreich. Dabei kann, wie in Abbildung 16 markiert werden, in welchen Bereichen Zusammenhänge bestehen. Darüber hinaus kann mit Hilfe von farblichen Markierungen gleichbleibende Elemente die gleiche Farbe zugeordnet werden.
In unserem Beispiel (vgl. Abbildung 17) hat die Schülerin darauf aufmerksam machen wollen, dass die Zeile 6 und die Zeile 12 in ihrer Sortierung gleich ist und somit nicht doppelt mitgezählt werden darf. Darüber hinaus nutzt sie rote Markierungen, wenn ein Betrag von einer zur nächsten Möglichkeit zerlegt wird. Daraus wird ersichtlich, an welchen Stellen Veränderungen von Zeile zu Zeile vorgenommen wurden. Rein sprachliche Erklärungen, die oft herausfordernd sind, werden damit an dieser Stelle umgangen.
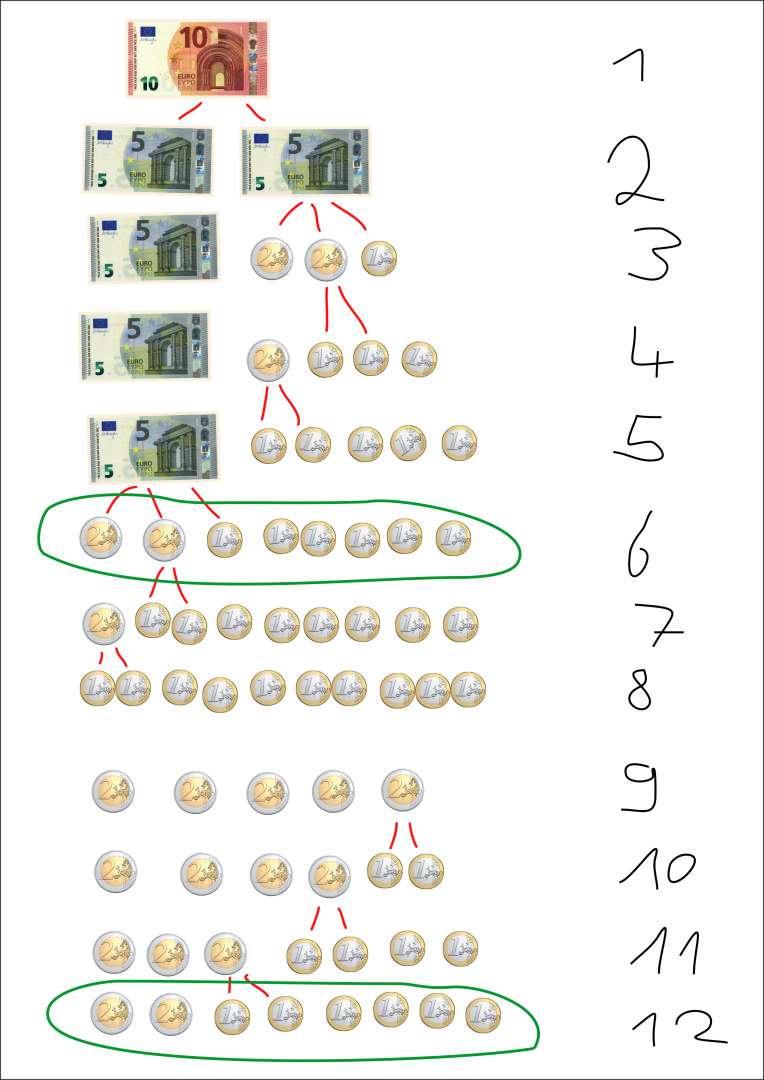 Abbildung 17 - Einsatz von Farbmarkierungen am Aufgabenbeispiel
Abbildung 17 - Einsatz von Farbmarkierungen am Aufgabenbeispiel
Pfeile
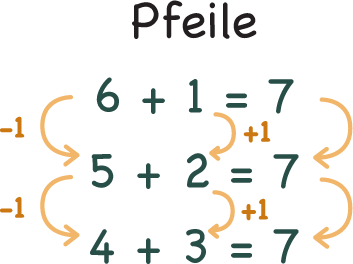 Abbildung 18 - Pfeile als Erkundungs-,
Abbildung 18 - Pfeile als Erkundungs-,
Darstellungs- und Erklärhilfe
Pfeile eignen sich besonders gut dafür, einen Prozess, eine Operation oder eine Veränderung darzustellen. Die Frage „Was passiert von hier nach dort?“ leuchtet Kindern meist intuitiv ein. So können wichtige mathematische Strukturen (wie hier das gegensinnige Verändern) entdeckt oder ein bestimmtes Vorgehen festgehalten werden.
In Abbildung 19 markiert der Schüler die schrittweise Zerlegung von 10€. Er hat unterschiedliche Farben genutzt, um deutlich zu machen, ob ein Geldschein oder eine Münze zerlegt wurde (roter Pfeil) oder gleichgeblieben ist (gelber Pfeil). Da er zusätzlich Münzen und Scheine, die aus einer gemeinsamen Zerlegung stammen, räumlich nahe beieinander anordnet, entsteht ein recht übersichtlicher Zerlegungsbaum, an dem sein Vorgehen deutlich wird.
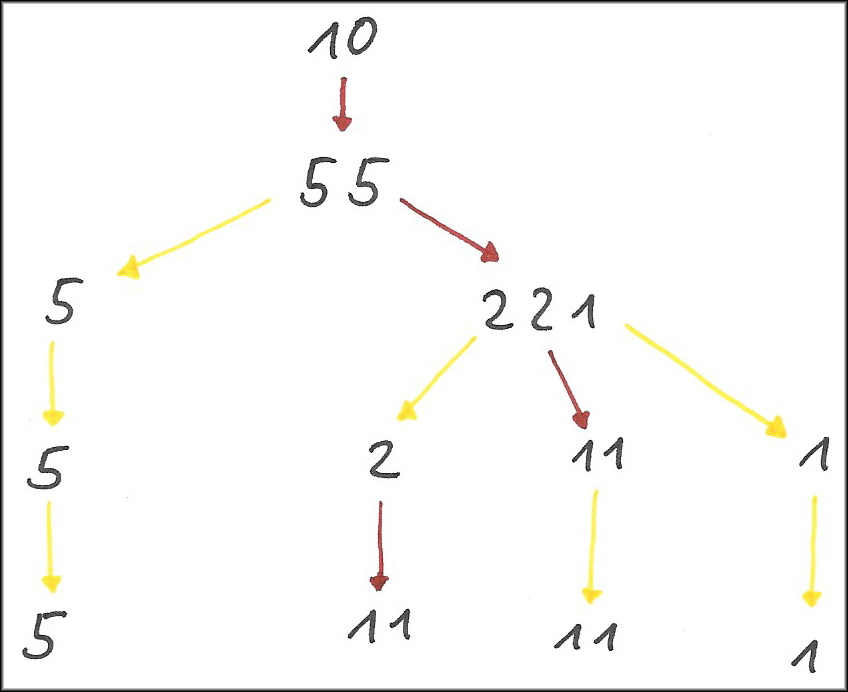 Abbildung 19 - Einsatz von Pfeilen am Aufgabenbeispiel
Abbildung 19 - Einsatz von Pfeilen am Aufgabenbeispiel
Tabellen
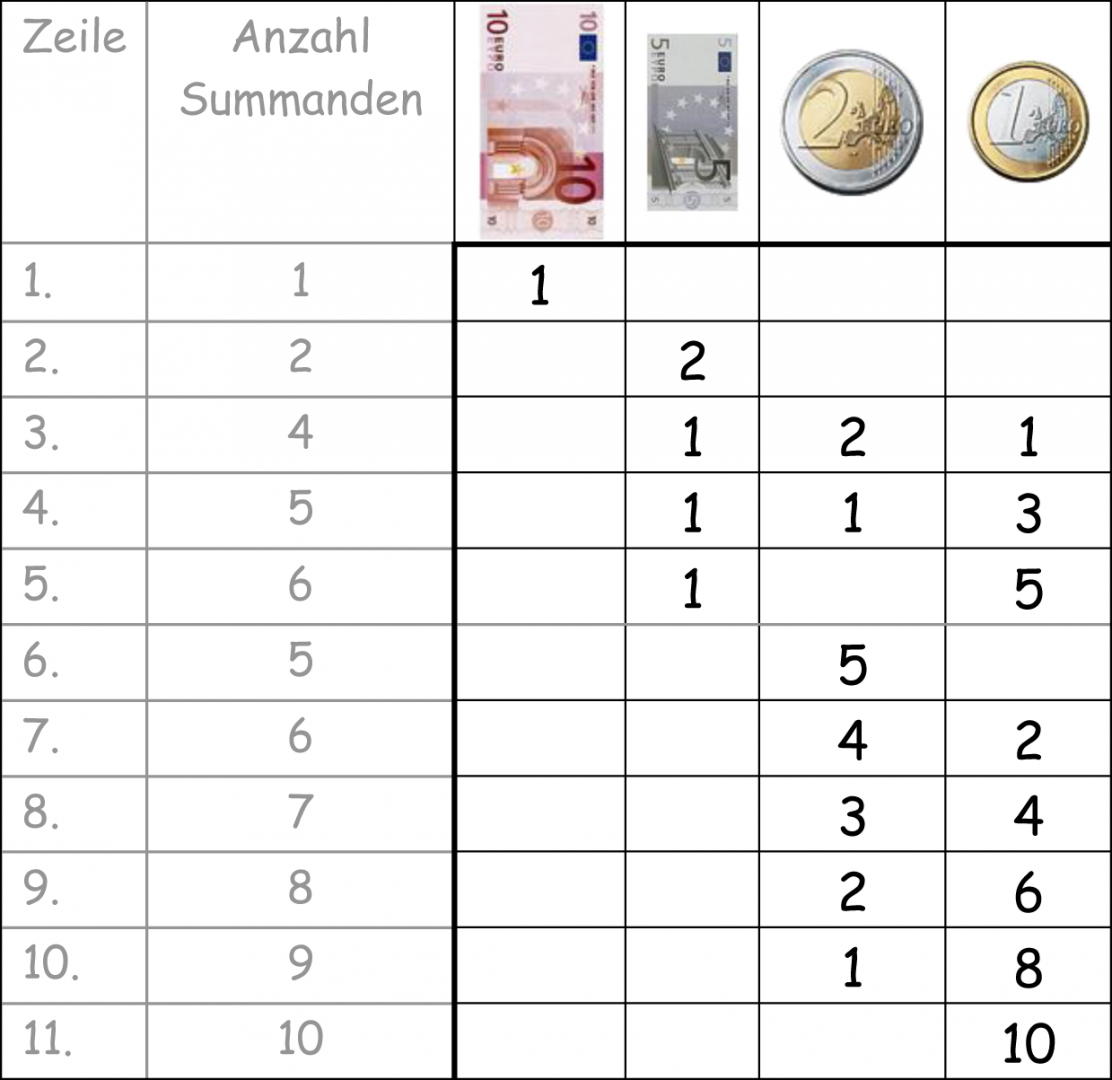 Abbildung 20 - Tabelle als mögliche Unterstützung des Erkundens und Darstellens
Abbildung 20 - Tabelle als mögliche Unterstützung des Erkundens und Darstellens
Um Lernende anzuregen, Ergebnisse systematisch zu notieren, eignen sich Tabellen besonders gut. Sie bieten z.B. die Möglichkeit, aufeinanderfolgende Schritte übersichtlich zu notieren oder – wie hier in Abb. 20 dargestellt – einen Bezug zur Stellenwerttafel herzustellen. Die Tabelle kann durch die zwei linken Spalten (ausgegraut) ergänzt werden. Die Aufführung der Zeilennummer bietet Unterstützung, wenn beim Austausch bspw. die Sortierung erklärt werden soll, indem einzelne Zeilen konkret benannt werden können. Die Zeile zum Eintragen der Anzahl der Summanden je Zerlegung dient als mögliches Sortierkriterium und ist damit eine Unterstützung beim Erkunden.
Sprachliche Unterstützung
Im besten Fall können sich die Kinder, wenn sie ihrem Partner im Austausch ihre Entdeckungen oder ihr Vorgehen erklären, auf eine Vielzahl von unterstützendem Maßnahmen beziehen, etwa auf ihre mit Forschermitteln erweiterten Lösungen, auf enaktives didaktisches Material oder auf systematische Notizen in Tabellenform. Trotzdem bleibt die Sprache im Austausch und der Ordnung eigener Gedanken unter Kindern ein wesentliches Instrument, sie hat damit eine Doppelfunktion:
-
neben der offensichtlichen kommunikativen Funktion besitzt sie ebenso eine
-
kognitive Funktion, nämlich das Nachdenken über und Ordnen der eigenen Gedanken.
Beide Aspekte bedingen sich gegenseitig (vgl. Maier & Schweiger, 1999). Die Förderung sprachlicher Fertigkeiten unterstützt die Lernenden demnach in allen drei Arbeitsfeldern aus dem Bereich Hintergrund – nicht nur, wie vielleicht angenommen, im Arbeitsfeld „Erklären Lernen“. Grundsätzliche Hinweise zur Sprachförderung im Mathematikunterricht finden sich bei primakon: Übergreifendes – Vielfalt – Sprachförderung – Einstieg und bei PIKAS: Haus 4: Sprachbildung – Fortbildungsmaterial – Grundlegendes.
Im Förderkommentar Sprache des Zahlenbuches schlagen Götze und Hang (2017) drei Schwerpunkte der Sprachförderung vor: (1) Fachwortschatz aufbauen, (2) Sprachverständnis sichern und (3) Mathematische Kommunikation fördern.
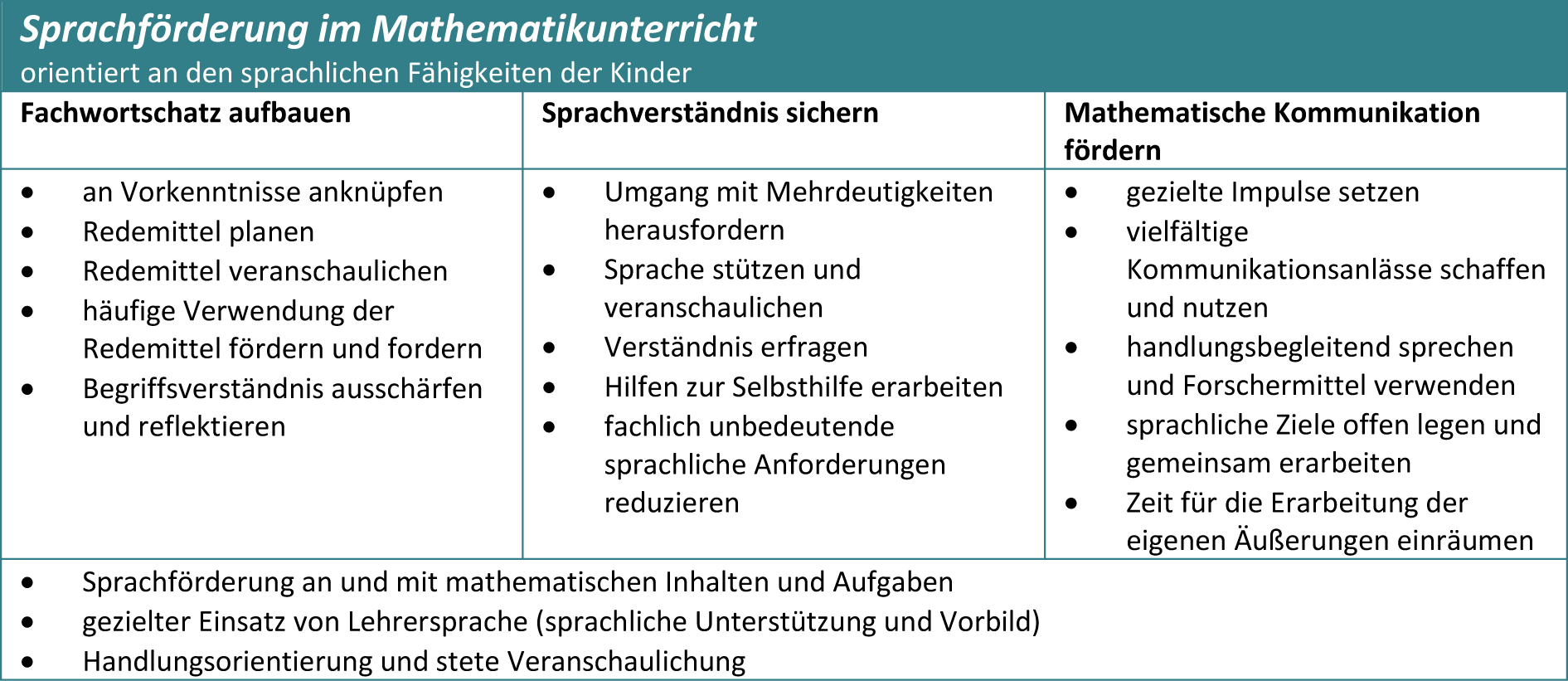 Abbildung 21 - Sprachförderung im Mathematikunterricht (vgl. Götze & Hang, 2017, 5)
Abbildung 21 - Sprachförderung im Mathematikunterricht (vgl. Götze & Hang, 2017, 5)
Damit Lernende für die Erklärung „ihrer Denkprozesse [und -produkte] eine Sprache finden, die zum tragfähigen Medium ihrer Denkbewegungen“ (Schütte, 2002, 17) wird, benötigen sie, zusätzlich zu den schon genannten Medien, beispielsweise die Möglichkeit, (Fach-)Wörter zu sammeln und ihre Bedeutung zu diskutieren und Hilfestellungen bei der Formulierung von – für sie komplexen – Aussagen. Die Erstellung eines Wortschatzes ist also eine naheliegende Maßnahme, um den ersten Schwerpunkt „Fachwortschatz aufbauen“ zu unterstützen. Trotzdem bietet natürlich das gesamte Aufgabenformat und die zugehörigen Unterstützungsmaßnahmen Anlässe zur mathematischen Sprachförderung, bspw. können zahlreiche Kommunikationsanlässe geschaffen werden, das handlungsbegleitende Sprechen unter Zuhilfenahme von Material oder Forschermitteln wird angeregt und die häufige Verwendung von Redemitteln eingefordert.
Wortspeicher – Fachwortschatz aufbauen
Ziel des Aufbaus des Fachwortschatzes liegt in der Förderung der Nutzung von Bildungs- und Fachsprache. Die Lernenden müssen dabei unterstützt werden, Fachwörter und Redemittel zur mündlichen oder schriftsprachlichen Darstellung von Lösungen zu nutzen. „Durch die kontinuierliche Verwendung, Wiederholdung und Ausdifferenzierung werden die Ausdrücke fest im Langezeitgedächtnis der Kinder verankert und zunehmend selbstverständlicher genutzt“ (Götze & Hang, 2017, 5).
Verschiedene Aufgabenformate benötigen häufig spezielle Begriffe, um präzise Arbeitsaufträge und Lösungsprodukte formulieren zu können. Zu der Zerlegung von Geldbeträgen gehören eine ganze Reihe von Begriffen, die von den Schülerinnen und Schülern erst erlernt werden müssen. Zusätzlich werden in der Fachsprache im Mathematikunterricht häufig „Begriffe aus der Alltagswelt verwendet, ihnen aber eine andere, spezifische Bedeutung zugeteilt“ (Schütte, 2002, 16). Wird also zum Beispiel der Unterschied des alltagssprachlichen Begriffs „Möglichkeit“ zur hier spezifischer gemeinten Bedeutung nicht reflektiert, können sich Verständnisprobleme ergeben. Ähnliches lässt sich bei dem Begriff „Schein“ erkennen, der in der Alltagssprache mit den Begriffen Parkschein, Lottoschein oder Mondschein eine andere Bedeutung als der Schein in der mathematischen Fachsprache trägt.
Ein themenbezogener Wortspeicher kann dazu beitragen, die Kinder darin zu unterstützen sich aufgabenbezogen und mathematisch prägnant zu äußern. In diesem Fall könnte eine solche Sammlung exemplarisch folgendermaßen aussehen:
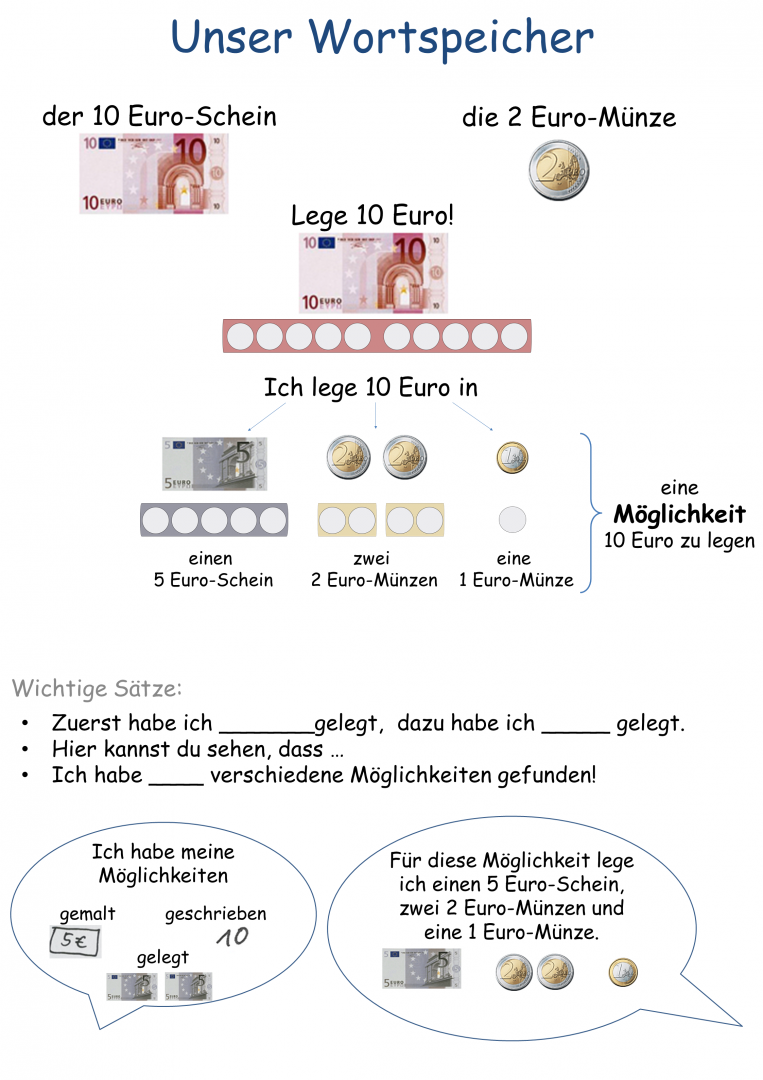 Abbildung 22 - Wortspeicher "Lege 10 Euro!"
Abbildung 22 - Wortspeicher "Lege 10 Euro!"
Gesprächsregel-Plakat
Um den Austausch zwischen Kindern allgemein zu strukturieren und ihnen Hilfestellungen für die einzelnen Gesprächsphasen mitzugeben, kann das Mathekonferenzen-Tipps-Plakat von PIKAS: Haus 8: Guter Unterricht – Unterrichtsmaterial – Mathekonferenzen genutzt werden. Für das aktuelle Teilmodul „Dem eigenen Denken auf der Spur“ ist vor allem der erste Punkt „Zeigt und erklärt eure Ideen und Ergebnisse!“ relevant.
 Abbildung 23 - Tipps für Mathe-Konferenzen
Abbildung 23 - Tipps für Mathe-Konferenzen
Es bietet sich aber auch an, gemeinsam mit den Kindern ein Gesprächsregelplakat zu erstellen, dass an die Aufgabenstellung und die Kompetenzen der Kinder angepasst ist. In Abgrenzung zum (allgemeineren) Mathekonferenzen-Tipps-Plakat sind dann konkretere Hilfestellungen denkbar, wie bspw. „Ich zeige mit meinem Finger auf meine Darstellungen, wenn ich etwas erkläre!“. Wie hilfreich ein solcher Tipp sein kann und um wieviel aussagekräftiger eine rein verbale Erklärung dadurch wird, zeigt sich auch im Beispiel der Schüler-Erklärungen zu den Zahlenmauern aus dem Hintergrund. Ohne die Darstellung des Schülerproduktes und der Markierungen, auf welchen Teil davon gezeigt wurde, würde ein Großteil der relevanten Informationen nicht transportiert werden.
Die folgenden Hilfestellungen könnten auf diesem Plakat stehen:
-
Ich suche einen geeigneten Platz, an dem mein Partner/ meine Partnerin meine Ergebnisse gut sehen können und wir ein bisschen Ruhe haben.
-
Ich zeige mit meinem Finger auf meine Darstellungen, wenn ich etwas erkläre.
-
Ich erkläre meine Darstellung.
-
„Hier habe ich einen 5€-Schein hingemalt!“
-
Ich nutze Wörter und Sätze aus dem Wortspeicher zur Hilfe.
-
Ich schaue meinem Zuhörer in die Augen.
-
Ich überprüfe, ob mein Partner/ meine Partnerin meine Darstellung verstanden hat.