Im Teilmodul „Vorerfahrungen berücksichtigen“ wurde bereits thematisiert, wie wichtig es für den langfristigen Kompetenzaufbau im Mathematikunterricht ist, etwaige Lücken in den Verstehensgrundlagen der Lernenden zu identifizieren und diese durch verständnisorientierte Förderung zu schließen, anstatt kurzfristig im aktuellen Unterrichtsstoff zu reparieren (Prediger, Freesemann, Moser Opitz & Hußmann, 2013, S. 10). Der Fokus in diesem Teilmodul liegt nun darauf, wie Verstehensgrundlagen, die für langfristige Lernprozesse besonders relevant sind, zusammengefasst und im Unterricht gefördert werden können. Im Weiteren werden diese Verstehensgrundlagen basale mathematische Kompetenzen bzw. mathematische Basiskompetenzen genannt. Die Ständige Wissenschaftlichen Kommission der Kultusministerkonferenz (SWK, 2022, S. 50) definiert diese wie folgt:
Unter basalen mathematischen Kompetenzen werden diejenigen Verstehensgrundlagen gefasst, ohne die ein erfolgreiches, nachhaltig verständiges und weiterführendes Mathematiklernen im Mathematikunterricht nicht möglich ist. […] Basale Kompetenzen werden im Elementar-, Primar- und Sekundarbereich kontinuierlich aufgebaut.
Die Relevanz von verstehensorientierter Förderung wird oft – und gerade bei Lernenden mit Schwierigkeiten im Mathematiklernen – nicht ausreichend berücksichtigt. Stattdessen liegt der Fokus häufig auf der Förderung reiner Rechenfähigkeiten, da standardisierte Vorgehensweisen vermeintlich Sicherheit und Erfolgserlebnisse versprechen. Wirklich nachhaltig ist Förderung aber – insbesondere für Kinder mit Schwierigkeiten im Mathematiklernen – wenn sie sich am Aufbau von Verständnis orientiert (Häsel-Weide & Prediger, 2017, S. 5).
Was bedeutet es, etwas verstanden zu haben? Laut Gerster und Schulz (2004) bedeutet verstehen lernen, „ein reichhaltiges Geflecht von Beziehungen herzustellen zwischen verschiedenen Darstellungen, Vorstellungen und Anwendungssituationen“ (S. 33). Somit ist zentral, dass bei den „Lernenden zunächst inhaltliche Vorstellungen für mathematische Konzepte und Operationen aufgebaut werden“ (Abraham et al., 2023, S. 3). Häufig werden diese Vorstellungen auch als „Grundvorstellungen“ bezeichnet. Dabei handelt es sich um
„gedankliche Modelle, die das Übersetzen zwischen unterschiedlichen Darstellungsebenen ermöglichen. Gegenstand dieser Übersetzungen sind dabei mathematische Objekte und Beziehungen. Grundvorstellungen können den Zusammenhang zwischen Symbolen oder Zeichen und anderen Darstellungen (Bildern, konkreten Repräsentanten) herstellen“ (Schulz und Wartha, 2021, S. 10).
Grundvorstellungen beschränken sich dabei nicht nur auf Zahlen oder Operationen, auch z.B. zu Rechenwegen können Grundvorstellungen aufgebaut und aktiviert werden (ebd., S. 11).
Wie bereits angedeutet, gehört zum Verständnis eines Inhalts, Beziehungen zwischen Darstellungen herstellen zu können – also Darstellungen vernetzen zu können. Gemeint ist damit, strukturelle Analogien in Handlung, Bild, Sprache und Symbol zu identifizieren und zueinander in Beziehung setzen zu können. „Vernetzen geht über das Wechseln von Darstellungen hinaus, indem Lernende auch erklären sollen, wie einzelne Strukturelemente einer Darstellung in der nächsten zu finden sind“ (Abraham et al., 2023, S. 3).

Abbildung 1: Darstellungsvernetzung (Handreichung „Mathematik gemeinsam Lernen“, S. 10 – pikas-mi.dzlm.de/node/713)
Nachdem hier zunächst die Verstehensorientierung bei der Förderung von Basiskompetenzen im Allgemeinen hervorgehoben wurde, soll nun gezeigt werden, dass ein mathematischer Inhaltsbereich die verständige Entwicklung mehrerer Basiskompetenzen erfordert.
Basiskompetenzen zum Stellenwertverständnis
Dies wird im Folgenden am Beispiel des Inhaltsbereich Stellenwertverständnis aufgezeigt werden. Für dieses sind laut SWK die folgenden basalen Basiskompetenzen relevant (SWK, 2022, S. 50; siehe auch „Stellenwertverständnis“ bei PIKAS: https://pikas.dzlm.de/node/1949):
Verständnis des Prinzips der fortgesetzten Bündelung
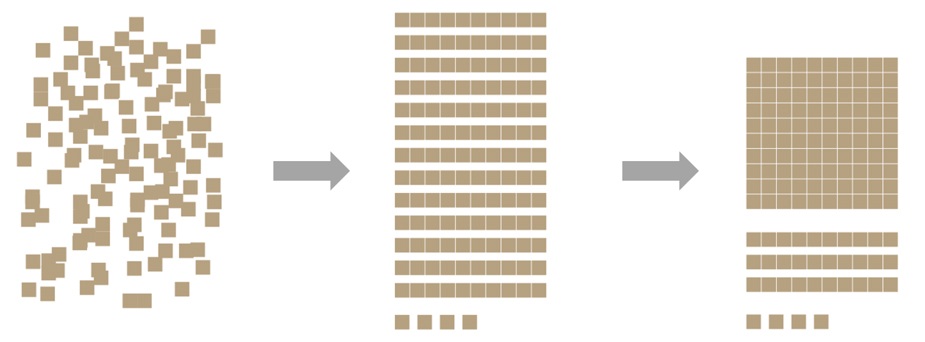
Abbildung 2: Prinzip der fortgesetzten Bündelung
Verstehen, dass jeweils zehn gleiche Objekte immer zu einem 10er-Bündel zusammengefasst und anschließend in den nächst höheren Stellenwert eingetauscht werden.
Verständnis des Prinzips des Zahlenwerts
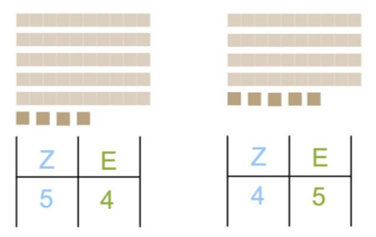
Abbildung 3: Prinzip des Zahlenwerts (pikas.dzlm.de/node/1949)
Verstehen, dass der Wert der Ziffer an einer bestimmten Position innerhalb der Zahl bzw. in der Stellenwerttafel die Anzahl der entsprechenden Bündel des Stellenwertes angibt: Eine 4 an der Einerstelle bedeutet vier Einer. Eine 5 an der Einerstelle bedeutet fünf Einer.
Verständnis des Prinzips des Stellenwerts
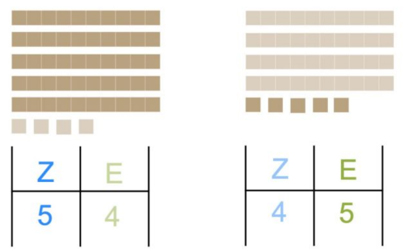
Abbildung 4: Prinzip des Stellenwerts (pikas.dzlm.de/node/1949)
Verstehen, dass die einzelnen Ziffern eines Zahlzeichens abhängig von ihrer Position innerhalb der Zahl bzw. in der Stellenwerttafel einen unterschiedlichen Stellenwert haben: Eine 5 an der Zehnerstelle bedeutet fünf Zehner. Eine 5 an der Einerstelle bedeutet fünf Einer.
Fähigkeit zur Darstellungsvernetzung
Die Sprech- und die Schreibweise sowie andere Darstellungen von Zahlen, die die Strukturen des Zehnersystems verkörpern, werden miteinander vernetzt. Dieses passiert zunächst mit Hilfe von Material und bildlichen Darstellungen und wird mit symbolischen Darstellungen verknüpft.

Abbildung 5: Darstellungsvernetzung des Zehnersystems (Orientierungsrahmen arithmetische Basiskompetenzen – pikas.dzlm.de/node/2410)
Ohne diese Basiskompetenzen ist „der Erwerb eines gesicherten Stellenwertverständnisses im Zahlenraum bis 1.000 genauso erschwert wie der Erwerb von Kompetenzen im additiven Rechnen im Zahlenraum bis 100“ (SWK, 2022, S. 50).
Welche Basiskompetenzen für den Elementar-, und den Primarbereich zentral sind, wird in den folgenden Abschnitten erläutert.
Vorschulische mathematische Basiskompetenzen
Im Lehrplan Mathematik für die Primarstufe in Nordrhein-Westfalen (MSB NRW, 2021, S. 81) wird der Begriff „grundlegende Vorläuferfähigkeiten“ genutzt, um frühe vorschulische mathematische Kompetenzen zu beschreiben, die für ein Weiterlernen in der Grundschule elementar sind. Dieser Begriff muss kritisch gesehen werden:
„Vorläuferfähigkeiten gibt es nicht. Jede Auseinandersetzung mit mathematischen Inhalten ist per se Mathematik und keine Vorform. […] Aus mathematik-didaktischer Sicht sollte möglichst die Mathematik als Ganzheit und Erfahrung, als lebenslanger Lernprozess angesehen werden.“ (Steinweg, 2008, S. 273)
Zudem kann eine nicht unproblematische „Sicht des Lernens in abgeschlossenen, unabhängigen Bereichen“ (Steinweg, 2008, S. 273) entstehen. Aus diesem Grund wird hier, wie Eingangs im Text benannt, der Begriff „vorschulische mathematische Basiskompetenzen“ genutzt, um Fähigkeiten zu beschreiben, die, „sofern Kinder diese beim Schuleintritt nur teilweise oder unzureichend mitbringen, […] zunächst aufgebaut [werden müssen], um ein erfolgreiches Weiterlernen zu gewährleisten“ (MSB NRW, 2021, S. 81). Die im Lehrplan formulierten vorschulischen Basiskompetenzen beziehen prozess- und inhaltsbezogene Kompetenzen mit ein. Diese werden im Folgenden benannt.
Basiskompetenzen, die sich auf die prozessbezogenen Kompetenzen beziehen (ebd.):
-
„Mathematik im Alltag entdecken und erforschen,
-
mathematische Situationen darstellen und darüber sprechen,
-
kreativ sein und Probleme mithilfe der Mathematik lösen“,
-
Basiskompetenzen, die sich auf inhaltsbezogene Kompetenzen beziehen (ebd.):
-
„Anzahlen bis 4 simultan erfassen,
-
unstrukturierte Anzahlen durch Abzählen ermitteln,
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich), Mengeninvarianz, Eins-zu-Eins-Zuordnung,
-
die Zahlenwortreihe bis 10 vorwärts aufsagen, den Richtungsbegriff rückwärts erkennen,
-
räumliche Beziehungen benennen (u. a. oben, unten, vorne, hinten),
-
Unterschiede oder Ähnlichkeiten wahrnehmen, klassifizieren, sortieren, Muster erkennen,
-
einfache geometrische Formen (Kreis, Dreieck, Viereck) erkennen“.
-
Zusätzlich werden Wahrnehmungs- und Koordinationsfähigkeiten (ebd.) formuliert, wie:
-
„Teilfiguren in einem komplexen Hintergrund erkennen und isolieren (Figur-Grund-Wahrnehmung) sowie
-
Seheindrücke und Handbewegungen koordinieren (Auge-Hand-Koordination)“.
Die Relevanz vorschulischer Basiskompetenzen für ein erfolgreiches Weiterlernen in der Grundschule ist empirisch belegt (z.B. Benz, Peter-Koop & Grüßing, 2015, S. 7ff). Gleichzeitig können unzureichende vorschulische Basiskompetenzen die Entstehung von Rechenschwierigkeiten in der Grundschule vorhersagen: So wurden Defizite in der Mengenerfassung (Invarianz, Mengenvergleich) und im Vorwissen über Zahlen (Zählfertigkeiten ebenso wie elementares Rechnen) als Risikofaktoren für die Entstehung von Rechenschwierigkeiten identifiziert (Krajewski, 2008).
Auch Basiskompetenzen, die sich auf die prozessbezogenen Kompetenzen beziehen, wie „Mathematik im Alltag entdecken und erforschen“, sind kein Beiwerk, sondern für das erfolgreiche Lernen im Mathematikunterricht der Primarstufe äußerst relevant. Inwiefern Kinder schon im Kindergarten gelernt haben, ihre Aufmerksamkeit auch auf mathematische Aspekte ihrer Umwelt zu lenken, hat entscheidenden Einfluss auf ihre (späteren schulischen) Fähigkeiten, Sachsituationen mathematisch zu interpretieren, wie auch auf ihre arithmetischen Leistungen in der Primarstufe insgesamt (Hasemann & Gasteiger, 2014, S. 34). So unterscheidet sich die Art der Wahrnehmung von mathematischen Objekten und Zusammenhängen bei Kindern in der ersten und zweiten Klasse z.T. deutlich voneinander:
„Wenn beispielsweise die Aufgabe lautet: ‚Tina und ihre Freundin Katja haben rote und gelbe Plastikbälle. Zusammen haben sie 8 Bälle, 5 davon sind rot. Wie viele Bälle sind gelb?‘, so gibt es Kinder, die sich bei einer solchen Sachaufgabe hauptsächlich für die realen Personen und realen Gegenstände interessieren und entsprechende Assoziationen herstellen (Wie heißen die genannten Kinder? Aus welchem Material sind die Bälle, und welche Farbe haben sie? Ich kenne ein Mädchen, das auch Tina heißt, und gestern haben wir auch mit einem roten Ball gespielt!). Kinder, die in einer Sachsituation ihre Aufmerksamkeit auf diese oder ähnliche äußere Aspekte richten, zeigen bei diesen Aufgaben [und in der Arithmetik insgesamt] deutlich schlechtere Leistungen als Kinder, die in derselben Situation ihre Aufmerksamkeit spontan auf die Zahlen und ihre Beziehungen richten, also auf die mathematische Struktur, die der Aufgabe zugrunde liegt.“ (Hasemann & Gasteiger, 2014, S. 34)
Anregungen für die Förderung vorschulischer Basiskompetenzen für Kinder im Kindergartenalter sind im Unterrichtsteil dargestellt.
Mathematische Basiskompetenzen für den Primarbereich
Auch bei den schulischen mathematischen Basiskompetenzen spielen die prozessbezogenen Kompetenzen eine zentrale Rolle: „Die Entwicklung der prozessbezogenen mathematischen Kompetenzen ist für die Nutzung der Mathematik im Alltag und insbesondere für eine erfolgreiche Teilnahme am (weiterführenden) Mathematikunterricht unverzichtbar. […] [Ihre Förderung] ist zudem von entscheidender Bedeutung auch für die Sicherung der inhaltsbezogenen mathematischen Kompetenzen“ (SWK, 2022, S. 51).
Die prozessbezogenen vorschulischen Basiskompetenzen (s.o.) werden in der Primarstufe kontinuierlich weiter entwickelt und ausdifferenziert zu den Kompetenzbereichen
-
Problemlösen (Erkunden, Lösen, Reflektieren),
-
Modellieren (Strukturieren, Mathematisieren, Interpretieren),
-
Kommunizieren (Beschreiben, Dokumentieren, Kooperieren),
-
Argumentieren (Vermuten, Begründen, Überprüfen) und
-
Darstellen (Verstehen, Verwenden, Vernetzen) (MSB NRW, 2021, S. 78).
Auf Seiten der inhaltsbezogenen Kompetenzen wird ein klarer Fokus auf die arithmetischen Kompetenzen gelegt, da diese von besonderer Bedeutung sind – sowohl für die Nutzung der Mathematik im Alltag als auch für die erfolgreiche Teilnahme am weiterführenden Mathematikunterricht. Übereinstimmend dazu formuliert die Ständige Wissenschaftlichen Kommission der Kultusministerkonferenz (SWK, 2022) auch nur arithmetische Basiskompetenzen im Primarbereich – andere Inhaltsbereiche werden an dieser Stelle ausgelassen. Dabei geht es in den einzelnen hier genannten Kompetenzbereichen grundsätzlich immer um „Sicherheit im Gebrauch, um Verständnis und um Flexibilität“ (ebd. S. 51).
Zentrale arithmetische Inhaltsbereiche und zugrundeliegende Basiskompetenzen sind laut SWK (ebd., S. 51f):
-
tragfähiges Zahlverständnis: Grundvorstellungen zu Zahlen, Fähigkeit zur Darstellungsvernetzung, insbesondere der verständige Umgang mit flächigen und linearen Darstellungen, Nutzung von Zahlbeziehungen und quasi-simultane Zahlauffassung,
-
tragfähiges Stellenwertverständnis: Prinzip der fortgesetzten Bündelung, Prinzip des Stellenwerts und Prinzip des Zahlenwerts und Fähigkeit zur Darstellungsvernetzung,
-
tragfähiges Operationsverständnis: Grundvorstellungen zu den Operationen, Fähigkeit zur Darstellungsvernetzung, Nutzung von Beziehungen zwischen Aufgaben und Rechenoperationen,
-
arithmetische Basisfakten: Aufgaben des kleinen Einspluseins, Einminuseins, Einmaleins und Einsdurcheins, Erwerb durch Nutzung von Aufgabenbeziehungen, mit dem Ziel, die Geläufigkeit von Ableitungsstrategien zu erhöhen,
-
mündliche und halbschriftliche Rechenanforderungen: Nutzung von auf Rechengesetzen beruhenden Rechenstrategien, Fähigkeit zur Darstellungsvernetzung, sicherer Strategiegebrauch
-
schriftliche Rechenanforderungen: Verständiges und damit sicheres Nutzen von Algorithmen.
Einen guten Überblick über die diesen Kompetenzbereichen zugrundeliegenden Basiskompetenzen gibt der „Orientierungsrahmen Arithmetische Basiskompetenzen“ von PIKAS (pikas.dzlm.de/node/2410). In diesem werden nicht nur die einzelnen Basiskompetenzen strukturiert dargestellt, sondern auch unter Bezugnahme auf konkrete Beispiele veranschaulicht. Er kann dadurch praktikable Arbeits- und Planungshilfe für den Unterricht sein, der verdeutlicht, welche (arithmetischen) Kompetenzen Lernende im Verlauf der Primarstufe erwerben können sollen (vgl. Abb. 6).

Abbildung 6: Orientierungsrahmen „Arithmetische Basiskompetenzen“ von PIKAS (pikas.dzlm.de/node/2410)
Die Relevanz dieser Basiskompetenzen für das Weiterlernen im Mathematikunterricht wurde in didaktischen Analysen aufgezeigt und empirisch nachgewiesen (SWK, 2022, S. 50). Zudem zeigen die Ergebnisse der PISA-Studie (Reiss et al., 2019) und des IQB-Bildungstrends (Stanat et al., 2019), dass etwa 20 % der Jugendlichen am Ende der Sekundarstufe I „nur wenige Anforderungen bewältigen können, die über elementare Standardaufgaben hinausgehen, und teilweise auf Grundschulniveau rechnen“ (SWK, 2021, S. 50). Hierbei scheint es sich nicht um Schwierigkeiten zu handeln, die sich erst in der Sekundarstufe entwickeln: Auch am Ende der Primarstufe zeigen mehr als 20 % der Lernenden große Lücken in den Verstehensgrundlagen, was ein Weiterlernen in der Sekundarstufe erheblich erschwert (ebd.).
Die Bedeutung einzelner Basiskompetenzen für das Weiterlernen in der Sekundarstufe wird zum Beispiel am Thema „Bruchrechnung“ deutlich. Schulz und Wartha (2021, S. 230f) nennen hierfür Inhalte, die in der Primarstufe thematisiert werden sollten „da diese die Grundlage für einen erfolgreichen Bruchzahlen-Lehrgang in der Sekundarschule bilden können“ (ebd., S. 230). Dazu zählen unter anderem (ebd., 231):
-
Grundvorstellungen zu den Rechenoperationen Addition und Subtraktion mit natürlichen Zahlen und ggf. Brüchen,
-
Grundvorstellungen zur Multiplikation, insbesondere Verwendung von rechteckigen Darstellungen zur Veranschaulichung mit natürlichen Zahlen,
-
Grundvorstellungen zur Division, insbesondere des Messens/Aufteilens mit natürlichen Zahlen und ggf. mit Brüchen,
-
Grundvorstellungen zu Zahlen als Mengen- und Positionsangaben, insbesondere Verwendung des Zahlenstrahls und der
-
Zusammenhang zwischen der Multiplikation und Division als Umkehroperation.
Neben den verschiedenen grundlegenden Zahl- und Operationsvorstellungen wird hier auch die Bedeutung der Verwendung bestimmter Darstellungsformen für das Weiterlernen unterstrichen.
Mathematische Basiskompetenzen für den Sekundarbereich
Ein Orientierungsrahmen für mathematische Basiskompetenzen im Sekundarbereich ist aktuell weder in den Lehrplänen noch in der Fachliteratur so klar definiert, wie das für den Primarbereich bereits der Fall ist. Ein Überblick über orientierende Anregungen für zentrale Kompetenzen am Anfang der Sekundarstufe 1 bietet jedoch beispielsweise das Projekt „Mathe sicher können“. Dort wird unter anderem zu folgenden grundlegenden Sekundarstufenthemen Diagnose- und Fördermaterial bereitgestellt:
-
Brüche, Prozente und Dezimalzahlen
-
Brüche als Anteile
-
Gleichwertige Brüche verstehen
-
Brüche und Prozente ordnen
-
Mit Brüchen rechnen
-
Stellenwerte von Dezimalzahlen verstehen
-
Dezimalzahlen ordnen und vergleichen
-
Dezimalzahlen addieren und subtrahieren
-
Dezimalzahlen multiplizieren und dividieren
-
Zusammenhang Dezimalzahlen – Brüche
-
Sachrechnen
-
Längen- und Flächeninhalte verstehen
-
Schätzen
-
Textaufgaben
-
Diagramme verstehen und nutzen
-
Proportionalität verstehen
-
Prozentverständnis
Außerdem ist für den Sommer 2024 die Veröffentlichung einer Empfehlung zu den Basiskompetenzen für die Sekundarstufe der Ständigen Wissenschaftlichen Kommission der Kultusministerkonferenz geplant.
Im Unterrichtsteil soll nun die kontinuierliche Weiterentwicklung (SWK, 2022, S. 50) von Basiskompetenzen exemplarisch skizziert werden.