Basale Kompetenzen sollen im Elementar-, Primar- und Sekundarbereich kontinuierlich aufgebaut werden (SWK, 2022, S. 50). Wie dies in inklusiven Lerngruppen des Elementar- und Primarbereichs ausgestaltet werden kann, soll nun exemplarisch aufgezeigt werden.
Als mathematischer Inhaltsbereich wird hierfür die Entwicklung des Zahlverständnisses ausgewählt. Hierzu gehören mehrere Basiskompetenzen. Diese sind im
Elementarbereich (vorschulisch):
-
Anzahlen bis 4 simultan erfassen,
-
unstrukturierte Anzahlen durch Abzählen ermitteln,
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich), Mengeninvarianz, Eins-zu-Eins-Zuordnung,
-
die Zahlenwortreihe bis 10 vorwärts aufsagen, den Richtungsbegriff rückwärts erkennen
(MSB NRW, 2021, S. 81) und im
Primarbereich:
-
Grundvorstellungen zu Zahlen (kardinal und ordinal),
-
Fähigkeit zur Darstellungsvernetzung, insbesondere der verständige Umgang mit flächigen und linearen Darstellungen,
-
Nutzung von Zahlbeziehungen und
-
quasi-simultane Zahlauffassung
(SWK, 2022, S. 51f).
Im folgenden Teil werden jeweils zum Elementar- und Primarbereich beispielhafte Aktivitäten zum Aufbau des Zahlverständnisses beschrieben und daran jeweils aufgezeigt, welche Basiskompetenzen mit den Aktivitäten gefördert werden können.
Elementarbereich
Die mathematische Förderung von Basiskompetenzen im Elementarbereich sollte in erster Linie spielerisch erfolgen. „Spielen“ ist nicht nur die natürliche Aktivität der Kinder dieser Altersklasse, gute spielerische Förderung kann motivierender, leichter an unterschiedliche Lernniveaus anpassbar und mindestens ebenso effektiv sein wie Trainingsprogramme (Benz et al., 2017, S. 47f; Benz, Peter-Koop & Grüßing, 2015, S. 61f). Eine „didaktische Verschulung des Kindergartens“ (ebd.) bringt demnach keinen Mehrwert, vielmehr „kann konstatiert werden, dass das Spiel prinzipiell eine fördernde und die Kompetenzen des Kindes sichernde Kraft besitzt“ (Benz et al., 2017, S. 49).
Trotzdem muss festgehalten werden, dass auch spielorientierte Ansätze ein hohes Maß an professionellem Wissen aufseiten der pädagogischen Fachkraft erfordern, insbesondere wenn es darum geht, Kinder mit auffällig schwachen mathematischen Kompetenzen gezielt zu fördern (Benz, Peter-Koop & Grüßing, 2015, S. 62). Bestehen Unsicherheiten, was die kindliche mathematische Kompetenzentwicklung angeht, kann es sinnvoll sein, sich zunächst an Trainingsprogrammen zu orientieren.
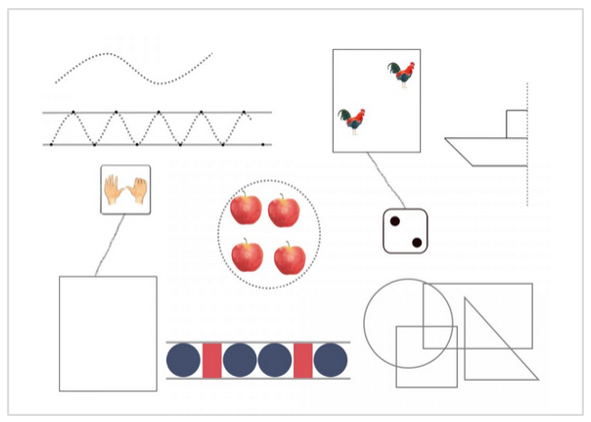
Abbildung 1: Ausschnitt aus dem Material zur frühen mathematischen Bildung (pikas.dzlm.de/node/1537)
Das „Material zur frühen mathematischen Bildung“ von PIKAS bietet mit einer Sammlung von Übungen, die zentrale vorschulische Basiskompetenzen fördern, Orientierung und zahlreiche Anregungen für weitere Aktivitäten.
Für das kindgerechte spielbezogene Mathematiklernen im Kindergartenalter nennen Benz, Peter-Koop & Grüßing (2015) unterschiedliche situative Anlässe und Aktivitäten, zu denen im Weiteren Beispiele vorgestellt werden:
-
teachable moments (spontane Interventionen in potentiell mathematisch gehaltvollen Situationen),
-
gemeinsames Lesen/ Betrachten von Bilderbüchern,
-
Konstruktions- und Bauspiele,
-
Rollenspiele und
-
Regelspiele.
Teachable moments
Ein wesentlicher Ansatzpunkt für die spielerische Förderung im Kindergartenalltag sind kurze, spontane Interventionen, in denen der mathematische Gehalt einer spielerischen Situation bewusst hervorgehoben wird.
„Zweifellos ist der sog. teachable moment eine äußerst fruchtbare Situation für den (mathematischen) Lernprozess. Leider […] verstreicht dieser Moment zu häufig ungenutzt. Für das Nutzen solcher Momente brauchen Erzieherinnen/Erzieher zum einen das für die effektive Begleitung frühen mathematischen Lernens notwendige Wissen für eine gezielte Intervention und zum anderen Zeit und Gelegenheit, Kinder bei ihrem Spiel ausführlich zu beobachten.“ (Benz, Peter-Koop & Grüßing, 2015, S. 65)
Eine Situation die im Alltag häufig auftritt und gut als „teachable moment“ genutzt werden kann, ist beispielsweise das Tisch decken:
Tisch decken
Die Kinder sollen einen Tisch für eine feste Anzahl von Personen decken (z.B. für das Mittagessen oder im Rollenspiel z.B. für eine Teeparty). Wichtig ist, den Fokus der Kinder darauf zu legen, dass es eine bestimmte Anzahl von Plätzen gibt und für jeden Platz feste Gegenstände gedeckt werden. Anregungen zur Umsetzung und zu Variationsmöglichkeiten finden sich in der Mathekartei von PIKAS auf Folie 2.
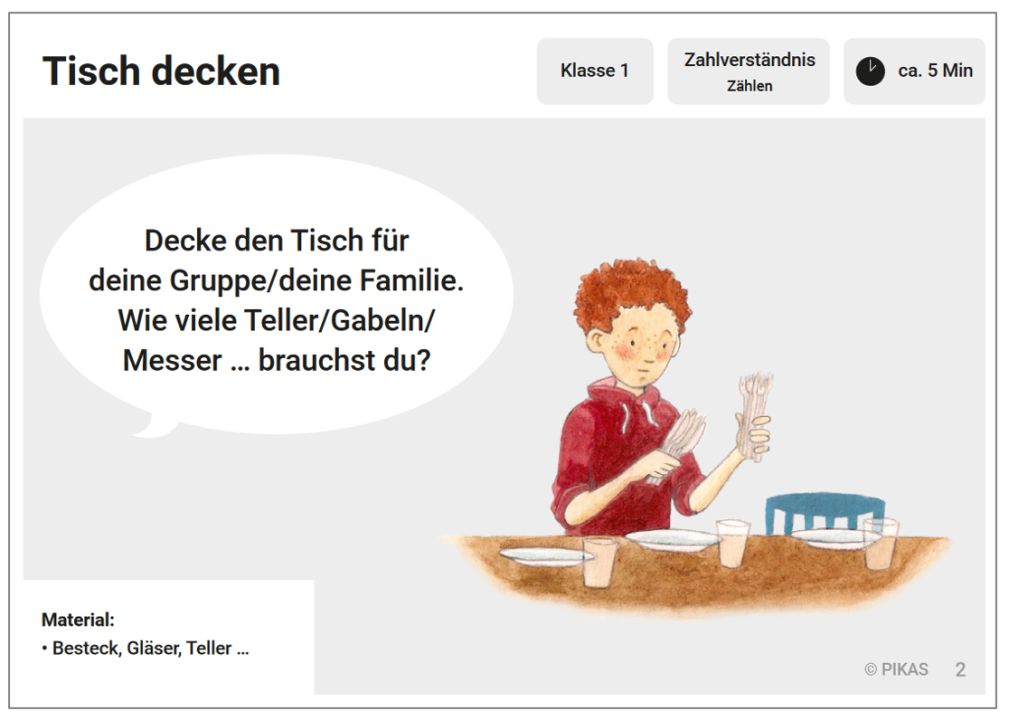
Abbildung 2: Vorderseite der Karte "Tisch decken" aus der „Mathekartei“ von PIKAS (pikas.dzlm.de/node/1632)
Wichtig ist es, in der Situation dann entsprechende Impulse zu stellen:
-
Wie viele Plätze werden benötigt? Was wäre, wenn noch eine Person mehr dazu kommt?
-
Wie viele Teller/Gabeln/Messer … benötigst du?
-
Hat jeder Platz einen Teller/eine Gabel/ein Messer?
Basale Kompetenzen, die hier gefördert werden können:
-
unstrukturierte Anzahlen durch Abzählen ermitteln (Anzahl der Plätze ermitteln),
-
Eins-zu-Eins-Zuordnung (jedem Platz genau ein Glas, eine Gabel, … zuordnen)
Gemeinsames Lesen / Betrachten von Bilderbüchern
Auch Bilderbücher bieten im Vorschulbereich vielfältige Anlässe, um mit Kindern lebensnahe Situationen aus der Perspektive der Mathematik zu betrachten. Hier finden Sie eine Liste mit gewinnbringenden Bilderbüchern.
Auch hier sind entsprechende Impulse notwendig, um über mathematische Inhalte ins Gespräch zu kommen, wie z.B.:
-
Wie viele … siehst du hier?
-
Wie viel ist das zusammen?
-
Wie viele sind es, wenn das hier dazukommt/weggeht?
-
Kennst du diese Zahl auf dem Schild? Was bedeutet sie?
Konstruktions- / Bauspiele
Konstruktions- und Bauspiele lassen sich vielfältig einsetzen, da sie von Kindern aller Altersgruppen gespielt werden können (etwa im Gegensatz zu Regelspielen, die vermehrt im letzten Kindergartenjahr zum Einsatz kommen). Insbesondere die Verwendung strukturierter Bauklötze bieten großes mathematisches Potential (ebd.). Wenn der Fokus nicht auf den räumlich-geometrischen Kompetenzen liegen soll, sondern auf der Förderung von Zahlvorstellungen, sollte die Aufmerksamkeit der Kinder durch gezielte Impulse auf Zahlaspekte gelenkt werden.
„Baue unterschiedliche Türme, mit 5 (6, 7, …) Steinen!“
 Abbildung 3: Unterschiedliche Türme mit 5 Steinen
Abbildung 3: Unterschiedliche Türme mit 5 Steinen
„Ordne die Türme nach der Größe! Wie viele Steine hast du hier… und hier… (etc.) benutzt?“
 Abbildung 4: Türme der Größe nach geordnet
Abbildung 4: Türme der Größe nach geordnet
Weitere Impulse könnten sein:
-
Welche Art von Stein passt hier wohl in die Lücke?
-
Bau dasselbe Muster nocheinmal (ggf. auch mit anderen Farben)?
-
Suche Zweier-/Vierer-/Sechser-Steine
Basale Kompetenzen, die hier gefördert werden können:
-
Anzahlen bis 4 simultan erfassen (bei kleinen Türmen),
-
unstrukturierte Anzahlen durch Abzählen ermitteln (bei großen Türmen),
-
Mengen vergleichen (beim Ordnen nach der Größe).
Rollenspiele
Rollenspiele ermöglichen es der Erzieherin oder dem Erzieher sowohl Aktivitäten zu initiieren und zu steuern, als auch Rollenvorbild zu sein, bei dem Kinder Handlungen zunächst beobachten können, um sie später, nach einem Rollenwechsel oder beim Spiel mit anderen Kindern, selbst umzusetzen. Um das Zahlverständnis zu fördern, eignen sich ganz unterschiedliche Spiele, die Anzahlaspekte fokussieren, wie z.B. „Kaufladen“.
Kaufladen
Die Spielsituation „Kaufladen“ ist seit etlichen Jahren ein Klassiker für mathematikhaltige Kontexte (Benz, Peter-Koop & Grüßing, 2015, S. 57). „Doch allein die Tatsache, dass ein Kaufladen in einer Einrichtung (oder zu Hause) zur Verfügung steht, ist noch keine Garantie für reichhaltige mathematische Lernprozesse. Dies liegt oft an der, was das Sortiment betrifft, zwar vielseitigen, für mathematisches Lernen aber dennoch nicht unbedingt hinreichenden Ausstattung“ (ebd.). Entscheidend ist, dass „im Sortiment“ genügend große Stückzahlen vorhanden sind, die die Kinder zum Zählen, Klassifizieren und Sortieren anzuregen – ein großes Sortiment mit jeweils nur ein bis zwei Stück pro Produkt ist hingegen nicht hilfreich (ebd.). Wichtig sind außerdem entsprechende Impulse und Aufträge:
-
Ich hätte gerne 5 Äpfel.
-
Wie viele Bananen möchtest du kaufen?
-
Wie viel kostet das?
-
Basale Kompetenzen, die hier gefördert werden können:
-
Anzahlen bis 4 simultan erfassen („Gib mir 4 Tüten!“, „Hier sind drei Euro.“),
-
unstrukturierte Anzahlen durch Abzählen ermitteln („Wie viele … haben Sie denn?“),
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich) („Haben Sie mehr … als … im Laden?“)
-
Fähigkeit zur Darstellungsvernetzung (konkrete Anzahl und Zahlwort).
Denkbar wäre auch ein Rollenspiel in einer Eisdiele: „Ich hätte gerne ein Eis mit drei Kugeln!“, „Wie viel kostet das?“, „Wie viel kostet ein Eis mit einer Kugel?“, „Wenn jeder hier zwei Kugeln bekommt, wie viele sind das dann?“
Regelspiele
Es existieren zahlreiche Regelspiele, die das Zahlverständnis fördern, die Spannweite reicht dabei von „klassischen Gesellschaftsspielen, die häufig im Rahmen einer „Spielesammlung“ in den Familien vorhanden sind, bis hin zu Lernspielen zu gezielt ausgewählten mathematischen Inhalten“ (ebd.).
Entscheidend, ob beim Regelspiel mathematische Lernprozesse angeregt werden oder nicht, ist – ähnlich wie beim Rollenspiel – nicht das Spiel selbst, sondern die gezielte Begleitung der erwachsenen Person. Diese kann, beispielsweise beim „Mensch-ärgere-dich-nicht“-Spielen, entweder nur auf die Einhaltung der Spielregeln achten oder durch intensive sprachliche Begleitung („Schau mal, wie … die Sechs gesetzt hat!“ [drei Zweierschritte], „Was musst du jetzt würfeln, damit deine Figur ins Haus kommt?“, „Wer hat schon die meisten Figuren in seinem Haus? Wie viele hast du mehr als ich?“) „das mathematische Potenzial der entstehenden Situationen in Bezug auf Simultanerfassung, Anzahlvergleich, Eins-zu-Eins-Zuordnung, Zählen in Schritten sowie Ordinal-/Kardinalzahlaspekt“ (ebd. S. 58) entfalten.
Unter diesem Link finden Sie eine Liste mit gewinnbringenden Regelspielen. Exemplarisch werden im Folgenden verschiedene Regelspiele vorgestellt.
Räuber und Goldschatz
Bei diesem Spiel aus dem „Handbuch produktiver Rechenübungen“ (Wittmann & Müller, 2017) üben die Kinder – unter anderem – das Vorwärts und Rückwärts zählen (auch in Schritten) im 20er-Raum. Hinweise zur Umsetzung und zu Variationsmöglichkeiten finden sich z. B. in der Mathekartei von PIKAS auf Folie 43.
Das Spiel läuft wie folgt ab:
-
Die Spielfiguren starten auf der 10, dort liegt der „Schatz“.
-
Ein Kind hat seine „Höhle“ bei der 1, es bekommt den Minuswürfel, das andere bei der 20, es bekommt den Pluswürfel.
-
Jedes Kind versucht den Schatz auf seine Seite zu ziehen.
-
Nun wird gewürfelt, wie viele Felder in die Richtung der eignen Höhle gezogen werden darf. Der Schatz wird abwechselnd nach links (minus) und rechts (plus) bewegt.
-
Wer zuerst mit dem „Schatz“ seine Höhle erreicht hat, hat gewonnen.

Abbildung 5: Vorderseite der Karte "Räuber und Goldschatz" aus der „Mathekartei“ von PIKAS (pikas.dzlm.de/node/1632)
Basale Kompetenzen, die hier gefördert werden können:
-
Anzahlen bis 4 simultan erfassen (und über die „4“ hinaus, etwa beim Erfassen der Würfelaugen),
-
unstrukturierte Anzahlen durch Abzählen ermitteln (beim Ziehen),
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich) („Wer ist näher am Ziel?“, „Um wie viel?“), Eins-zu-Eins-Zuordnung (beim Ziehen: ein Feld pro Würfelauge),
-
die Zahlenwortreihe bis 10 vorwärts aufsagen, den Richtungsbegriff rückwärts erkennen (und darüber hinaus, beim Vorwärts und Rückwärts Ziehen),
-
Fähigkeit zur Darstellungsvernetzung (konkrete Anzahl der Schritte, Zahlwort, Würfelbild und symbolische Darstellung auf dem Spielfeld)
Paarsuchspiel mit konkreten Gegenständen
Verschiedene Anzahlen von kleinen Steinchen (oder ähnlichen, gleichförmigen Material) werden unter Schüsseln verdeckt gelegt, mit jeweils immer zwei gleichen Anzahlen, damit Paare entstehen können. Wie beim bekannten Gedächtnisspiel müssen durch Aufdecken Paare gefunden werden. Die Kinder haben durch das konkrete Material die Möglichkeit abzuzählen, gleichzeitig müssen die Anzahlen (und die Positionen) mental gespeichert werden. Bei der Vorbereitung des Spiels bietet sich außerdem ein Gespräch darüber an, wie die Steinchen am besten (strukturiert) unter die Schälchen gelegt werden können, um das Erkennen der Anzahl (und auch das Abspeichern) zu erleichtern (Benz, Peter-Koop & Grüßing, 2015, S. 152).
Basale Kompetenzen, die hier gefördert werden können:
-
Anzahlen bis 4 simultan erfassen,
-
unstrukturierte Anzahlen durch Abzählen ermitteln („Passt mein Memory-Paar?“)
-
Quasi-simultane Anzahlerfassung (bei der Strukturierung von Anzahlen)
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich) („Um wie viel passt diese Schüssel nicht?“)
-
Fähigkeit zur Darstellungsvernetzung (konkrete Anzahl und Zahlwort).
-
Paare finden mit Darstellungsvernetzung
Hierfür werden Kärtchen mit unterschiedlichen Zahldarstellungen benötigt, also z.B. Würfelbilder, Fingerbilder, Ziffern und von den Kindern selbst produzierte Darstellungen. Genutzt werden können hierfür z. B. die Kärtchenvorlagen im „Material zur frühen mathematischen Bildung“ von PIKAS.
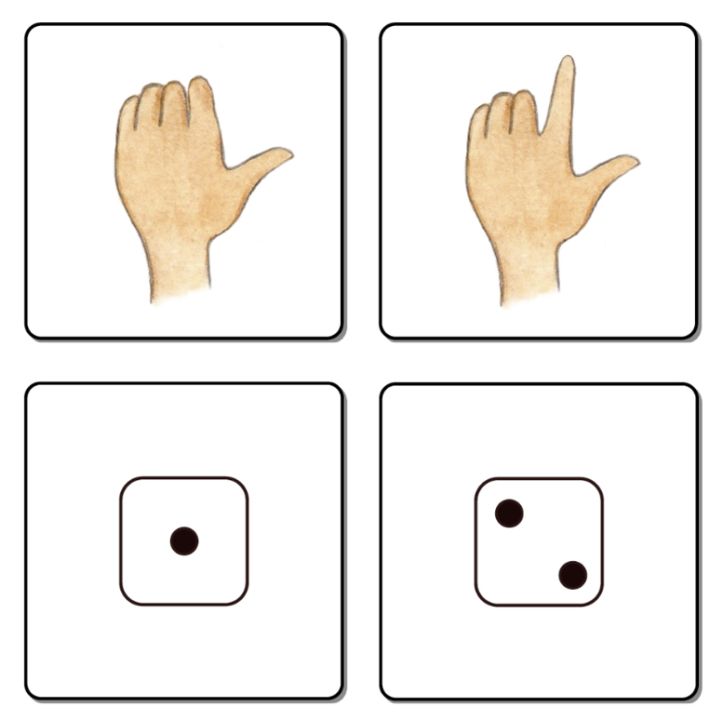
Abbildung 6: Kärtchenvorlagen im Material zur frühen mathematischen Bildung von PIKAS (pikas.dzlm.de/node/1537)
Die Karten einer Darstellungsart werden an einer Stelle ausgelegt, die einer anderen an einer anderen Stelle. Die Kinder haben nun die Aufgabe, sich ein Kärtchen zu nehmen und die Partnerkarte auf der anderen Seite zu finden. Variiert werden kann die Spielaufgabe beispielsweise durch die Nutzung von verschiedenen (mehreren) Darstellungen („Finde alle passenden Karten“), es kann außerdem verboten oder erlaubt sein, die Ausgangskarte mit zu nehmen. Als Erweiterung eignen sich die anspruchsvolleren und z.T. strukturierten „Zahldarstellungen – Zahlen von 1–20“ aus der Kartei „Mathematik zum Schulanfang“ von PIKAS.
Basale Kompetenzen, die hier gefördert werden können:
-
Anzahlen bis 4 simultan erfassen,
-
unstrukturierte Anzahlen durch Abzählen ermitteln („Passt mein Paar?“)
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich) („Um wie viel passt diese Karte nicht?“)
-
Fähigkeit zur Darstellungsvernetzung.
Primarbereich
Auch im Primarbereich bieten sich spielerisch orientierte Aktivitäten an, um die o.g. Basiskompetenzen zu fördern. Grundsätzlich werden dabei kontinuierlich größere Zahlenräume genutzt und zunehmend strukturierte und abstraktere Darstellungen miteinander vernetzt.
Die hier dargestellten Beispielaktivitäten stammen aus der schon o.g. Kartei „Mathematik zum Schulanfang“ von PIKAS, sowie aus dem Inhaltsbereich „Zahlvorstellungen“ auf dieser Seite.
Zahldarstellungen – Zahlen von 1–20 (Mathematik zum Schulanfang)
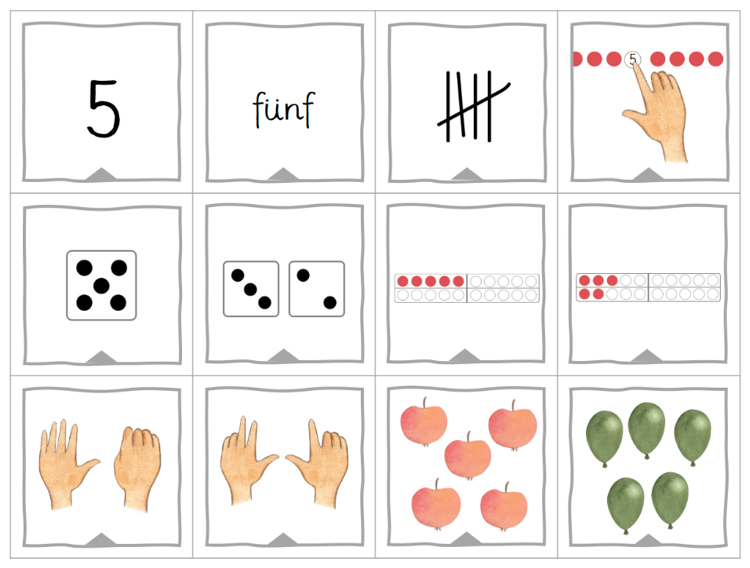
Abbildung 7: Unterschiedliche Darstellungen der "5" aus der Kartei „Mathematik zum Schulanfang“ (pikas.dzlm.de/node/2315)
Diese Sammlung von Zahldarstellungen vereint die wichtigsten Aspekte, die auch in den Basiskompetenzen genannt werden: Neben den symbolischen Darstellungen gibt es unstrukturierte Darstellungen, unterschiedlich strukturierte Darstellungen (auch lineare und flächige) und unterschiedliche Darstellungen von Zahlzerlegungen (Zahlbeziehungen).
Um die Vernetzung der Darstellungen zu fördern, eignen sich als spielorientierte Aktivitäten mit diesem Kartensatz z.B. „Memory“ (wie oben), „Quartett“, oder auch „Paare finden“ (wie im Abschnitt zum Elementarbereich). In der Kartei „Mathematik zum Schulanfang“ werden für den Umgang mit diesen Zahldarstellungen weitere (Kurz-) Aktivitäten vorgeschlagen.
Basale Kompetenzen, die hier gefördert werden können (grundsätzlich, abhängig von der jeweiligen Aktivität und den eingesetzten Impulsen, genauere Informationen zu den Kompetenzen finden sich auf den jeweiligen Folien der Kartei):
-
Anzahlen simultan erfassen,
-
unstrukturierte Anzahlen durch Abzählen ermitteln,
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich),
-
Fähigkeit zur Darstellungsvernetzung, insbesondere der verständige Umgang mit flächigen und linearen Darstellungen,
-
Nutzung von Zahlbeziehungen und
-
quasi-simultane Zahlauffassung, Zahlzerlegungen
An dieser Stelle wird die Aktivität „Schnelles Sehen“ exemplarisch genauer vorgestellt, da diese sich gut erweitern lässt.
Schnelles Sehen
Eine mögliche Umsetzung wird in der Kartei „Mathematik zum Schulanfang“ mit Erweiterungs- und Reduktionsmöglichkeiten beschrieben (vgl. Abbildung 8).
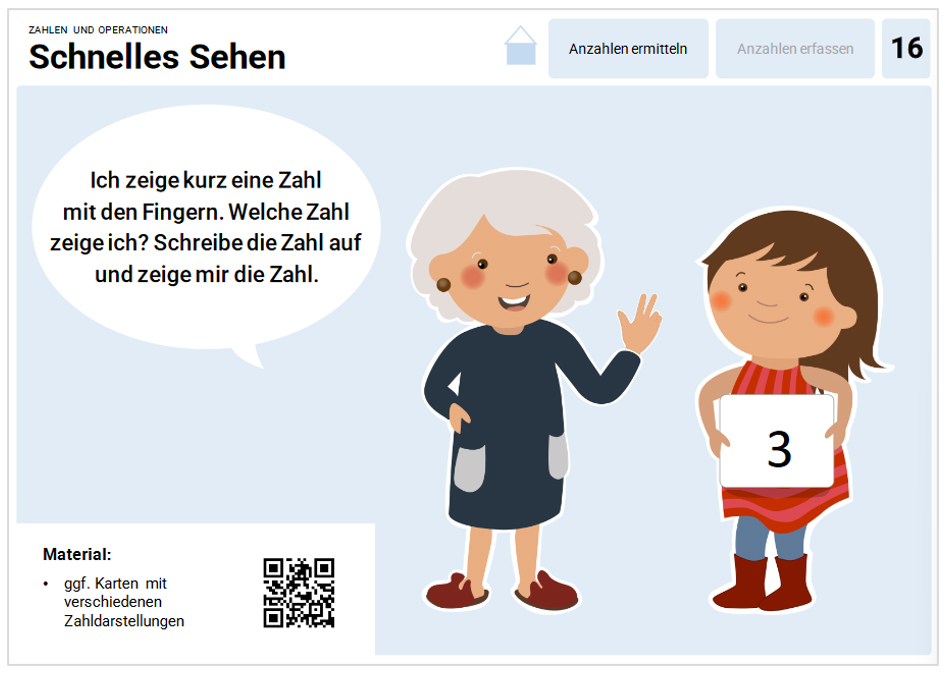
Abbildung 8: Vorderseite der Karte "Schnelles Sehen" aus der Kartei „Mathematik zum Schulanfang“ (pikas.dzlm.de/node/2315)

Abbildung 9: Rückseite der Karte "Schnelles Sehen" aus der Kartei "Mathematik zum Schulanfang" (pikas.dzlm.de/node/2315)
Anstatt eine Zahl mit Fingern zu zeigen, kann die Lehrkraft also auch eine strukturierte Darstellung nutzen, die schnell gesehen werden muss. Die eingeforderte Erklärung „Woran hast du das so schnell gesehen?“ spielt bei der Förderung der quasi-simultanen Zahlerfassung eine entscheidende Rolle.
Unter der Rubrik „Inhalte“ gibt es auf dieser Seite außerdem die Basisaufgabe „Schnelles Sehen“, die zu zweit gespielt werden kann, für inklusive Lerngruppen erstellt worden ist und weitreichende Reduktions-, Erweiterungs- und Unterstützungsmöglichkeiten aufzeigt. Wesentlich an der Aufgabenstellung ist aber, dass sie im Verlauf der Primarstufe, bei der kontinuierlichen Erweiterung des Zahlenraums, analog einsetzbar ist.
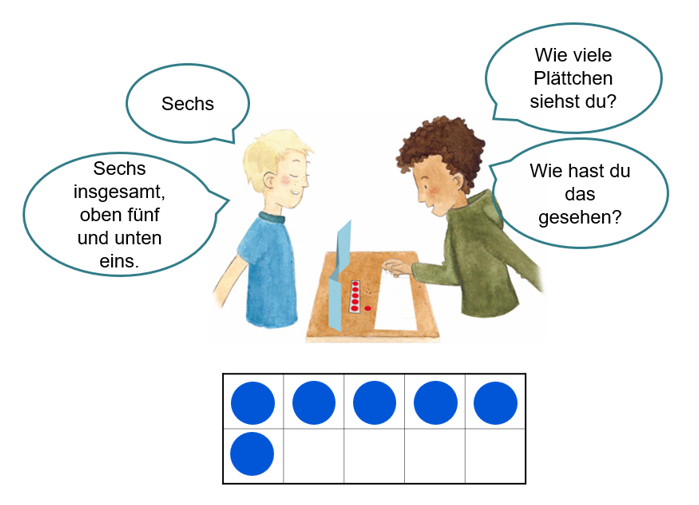
Abbildung 10: Basisaufgabe "Schnelles Sehen" (pikas-mi.dzlm.de/node/633)

Abbildung 11: Verschiedene strukturierte Zahldarstellungen zur Basisaufgabe "Schnelles Sehen" (pikas-mi.dzlm.de/node/633)
Basale Kompetenzen, die hier gefördert werden können:
-
Anzahlen simultan erfassen,
-
unstrukturierte Anzahlen durch Abzählen ermitteln,
-
Mengen vergleichen (mehr, weniger, größer, kleiner, gleich),
-
Fähigkeit zur Darstellungsvernetzung, insbesondere der verständige Umgang mit flächigen und linearen Darstellungen,
-
Nutzung von Zahlbeziehungen und
-
quasi-simultane Zahlauffassung, Zahlzerlegungen
Ein zentraler Aspekt in der Unterrichtsplanung im mathematischen Anfangsunterricht stellt die Diagnostik dar. Dafür bieten sich kurze diagnostische Gespräche an, die als Grundlage für eine anschließende Förderung dienen. Anregungen für solche diagnostische Gespräche und eine passende Förderung finden sich in der Kartei „FÖDIMA“ (Förderorientierte Diagnostik im mathematischen Anfangsunterricht). Dort gibt es zu zentralen arithmetischen Inhalten der ersten beiden Schuljahre Karteikarten. Auf der Vorderseite befindet sich jeweils eine kurze diagnostische Basisaufgabe mit Beobachtungshinweisen sowie gezielten Impulsen. Auf der Rückseite werden Förderanregungen mit Bezug zu den diagnostischen Basisaufgaben gegeben, die mit Blick auf die Lernstände der Kinder adaptiert werden sollten. Sie können an unterschiedliche Unterrichtssettings (z. B. im Klassenverband, in Kleingruppen, im Tandem, …) angepasst werden.
Wie dies beispielhaft aussehen kann, wird hier an der Aufgabe „Anzahlen (quasi-)simultan erfassen“ gezeigt:
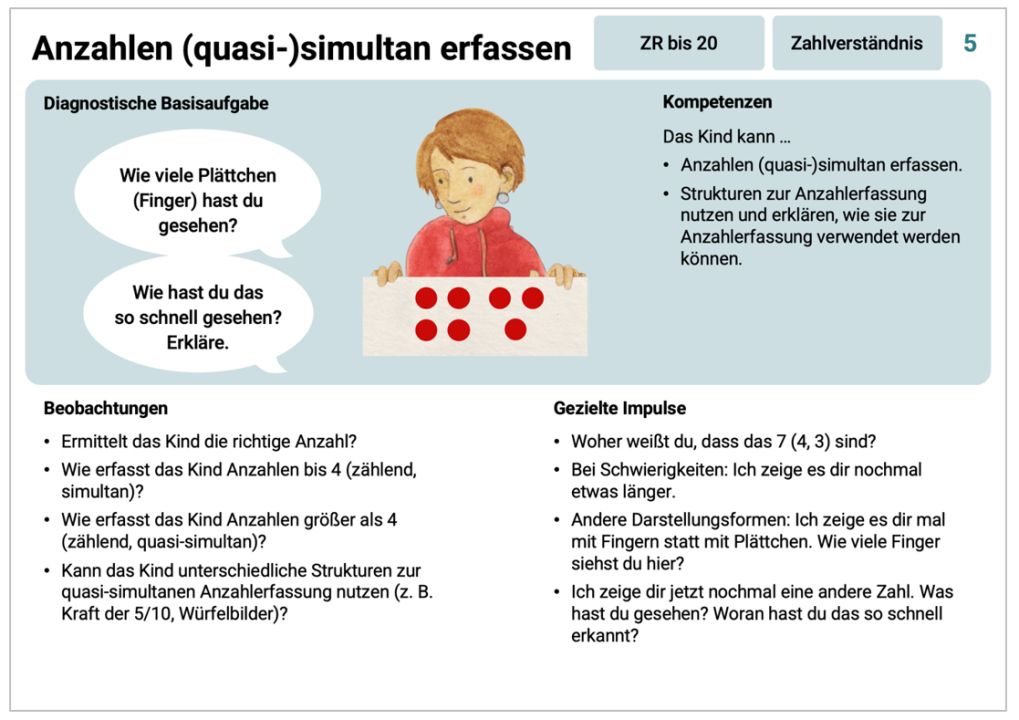 Abbildung 12: Vorderseite der Karte "Anzahlen (quasi)-simultan erfassen" aus der FÖDIMA-Kartei (pikas.dzlm.de/node/2557)
Abbildung 12: Vorderseite der Karte "Anzahlen (quasi)-simultan erfassen" aus der FÖDIMA-Kartei (pikas.dzlm.de/node/2557)
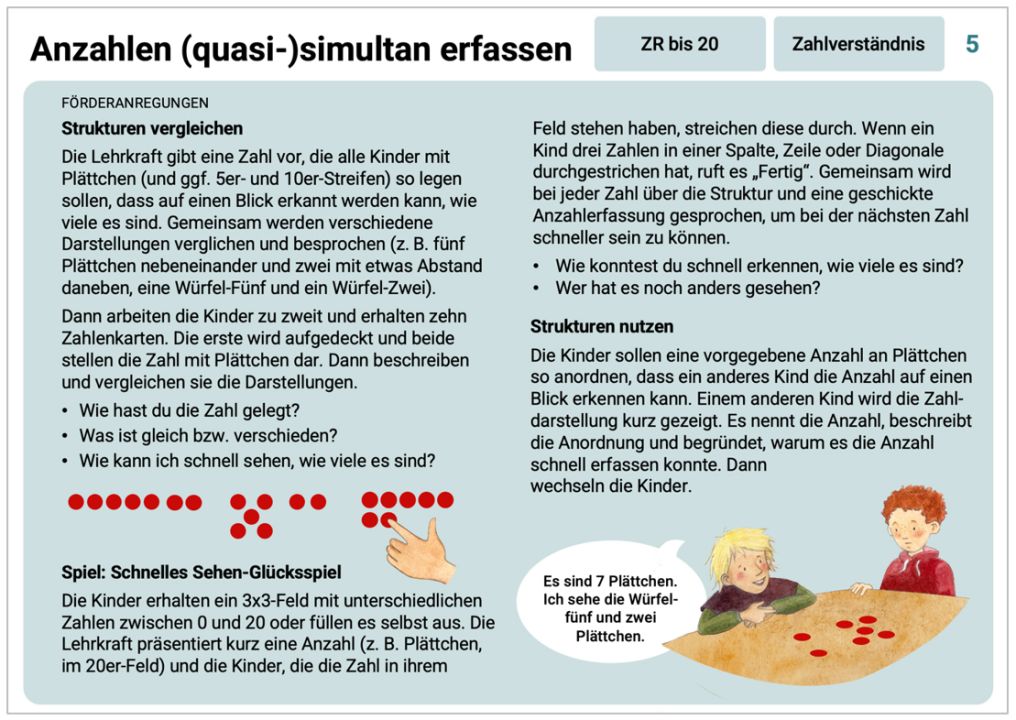 Abbildung 13: Rückseite der Karte "Anzahlen (quasi)-simultan erfassen" aus der FÖDIMA-Kartei (pikas.dzlm.de/node/2557)
Abbildung 13: Rückseite der Karte "Anzahlen (quasi)-simultan erfassen" aus der FÖDIMA-Kartei (pikas.dzlm.de/node/2557)
Insgesamt wird deutlich, dass für die Sicherung der mathematischen Basiskompetenzen im Kindergarten und der Primarstufe verschiedenste Spiele, Aufgaben und Aktivitäten in Frage kommen können. Inwiefern diese gewinnbringend eingesetzt werden können, hängt jedoch vor allem davon ab, wie diese von der Lehrperson begleitet werden.