Für die schriftliche Subtraktion gibt es mehrere mögliche Verfahren (siehe auch Hintergrund Ziffernrechnen). Schüler:innen sollten eines davon verständnisbasiert anwenden können. In der Grundschule entscheidet die Lehrkraft also, welches Verfahren im Unterricht thematisiert wird. In der Sekundarstufe I kann es sein, dass Schüler:innen in einer Klasse individuell verschiedene Verfahren nutzen.
In dieser Aufgabenstellung kompakt wird der Subtraktionsalgorithmus Stellenweise Abziehen mit Entbündeln thematisiert. Eine entsprechende Aufgabenstellung kompakt zum Subtraktionsalgorithmus Auffüllen / Stellenweise Ergänzen mit Bündeln finden Sie unter: Schriftlich subtrahieren (Auffüllen).
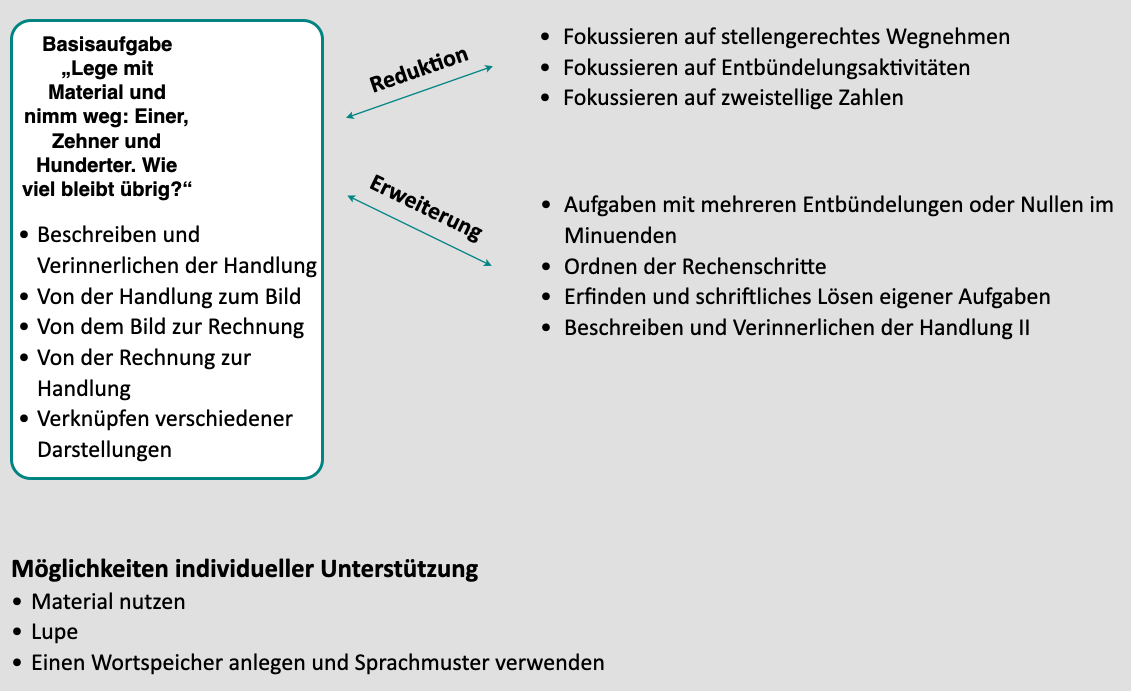 Abbildung 1: Aufgabenstellung kompakt
Abbildung 1: Aufgabenstellung kompakt
Basisaufgabe
„Lege mit Material und nimm weg: Zuerst die Einer, danach die Zehner und zum Schluss die Hunderter. Wie viel bleibt übrig?“
Die Aufgabenstellung kompakt fördert den Aufbau einer Grundvorstellung (vgl. Wartha & Schulz 2011, S. 5 ff.) zum Subtraktionsalgorithmus Stellenweise Abziehen mit Entbündeln, damit Kinder diesen nicht rezeptartig und somit fehleranfällig befolgen, sondern ihn verständnisbasiert einsetzen und erklären können. Ziel dieser Aufgabenstellung kompakt ist es weniger, einen Zusammenhang zwischen dem gestützten Kopfrechen auf der einen Seite und dem schriftlichen Algorithmus auf der anderen Seite herzustellen (vgl. hierzu aber PIK AS „Vom halbschriftlichen zum schriftlichen Subtrahieren“ und in einer videografierten Unterrichtsreihe die Umsetzung des Themenschwerpunkts). Es geht vielmehr darum, das Verfahren verstehensorientiert und materialgestützt zu erarbeiten.
Dazu sind die Aktivierung der entsprechenden Grundvorstellung der Subtraktion (Wegnehmen) sowie ein kardinales Zahl- und ein tragfähiges Stellenwertverständnis (siehe auch Modul Stellenwertvorstellungen) grundlegende Voraussetzungen. Der Aufbau einer Grundvorstellung kann durch die Nutzung und Vernetzung verschiedener Darstellungsformen (siehe auch Modul Darstellungsformen) mithilfe der folgenden Aufgabenstellungen gefördert werden.
Material: Aufgabenkarten, Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
Die Kinder erhalten eine Karte, auf der eine Zahl in ihren Bündelungseinheiten und der Anzahl der Bündel vorgegeben ist. Sie sollen diese Zahl zunächst mit Material legen. Dazu können sie Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen nutzen. Anschließend soll von dem gelegten Material eine weitere angegebene Zahl in der Reihenfolge „Zuerst die Einer, danach die Zehner und zum Schluss die Hunderter“ weggenommen und die übriggebliebene Menge notiert werden.
 Abbildung 2: Beispiel für eine Aufgabenkarte und mögliche Legematerialien
Abbildung 2: Beispiel für eine Aufgabenkarte und mögliche Legematerialien
Es bietet sich an, den Rechenweg zunächst gemeinsam durchzuführen und zu besprechen, damit Klarheit über das Vorgehen und die Aufgabenstellung herrscht. Beim Darstellen des auf der jeweiligen Karte symbolisch notierten Minuenden aktivieren die Kinder ihr kardinales Zahlverständnis und ihr Stellenwertverständnis. Nach dem Legen soll das Material stellenweise weggenommen werden. Wenn der Minuend an einem Stellenwert kleiner ist als der Subtrahend (im oben abgebildeten Beispiel bei den Zehnern), stößt man jedoch auf das Problem, dass nicht genug Material zum Wegnehmen vorhanden ist. Um das Problem zu lösen, muss erst der nächstgrößere Stellenwert entbündelt werden (im oberen Beispiel wird ein Hunderter in zehn Zehner getauscht), wodurch sich der Wert des Minuenden nicht verändert. Diese Idee können die Kinder eigenständig aufgrund von Vorerfahrungen mit dem Bündeln und Entbündeln am Material entwickeln. Sie können auch durch geeignete Impulse („Was könntest du tun, wenn du nicht genug Zehner zum Wegnehmen hast?“ / „Woher könntest du die Zehner nehmen?“ / „Wie viele Zehner sind in einem Hunderter?“ / …) zum Entbündeln angeregt werden.
Durch das Bearbeiten verschiedener Aufgabenkarten führen die Kinder handelnd Entbündelungsaktivitäten an unterschiedlichen Stellenwerten durch. Es werden zunächst Aufgaben mit nur einer Entbündelung thematisiert. Weiterführende Impulse wie „Wann musst du entbündeln und wann nicht?“ / „Warum darfst du entbündeln?“ können den Anstoß zu Verallgemeinerungen der Entdeckungen in einer Reflexionsphase geben. Um die Frage „Wie viel bleibt übrig?“ zu beantworten, müssen die Kinder die verbleibende Menge abschließend in die symbolische Darstellungsform zurückübersetzen.
Die Reihenfolge der Rechenschritte und die Grundvorstellung zur Subtraktion (Wegnehmen) ist in Anlehnung an den schriftlichen Algorithmus in der Aufgabenstellung vorgegeben, damit die Kinder Bezüge zwischen den verschiedenen Darstellungsformen des gleichen Rechenweges herstellen können.
Basisaktivität
Beschreiben und Verinnerlichen der Materialhandlung
Material: Aufgabenkarten, Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
In dieser möglichen Basisaktivität bearbeiten die Kinder weiterhin die vorherige Aufgabenstellung unter Nutzung desselben Materials (Aufgabenkarten, Legematerial): „Lege mit Material und nimm weg: Einer, Zehner und Hunderter. Wie viel bleibt übrig?“. Die Aufgabenstellung wird jedoch durch gegenseitige Beschreibungen mit und ohne Sicht auf das Material, beispielsweise in einer abwechselnden Partnerarbeit, in vier Phasen erweitert und vertieft:
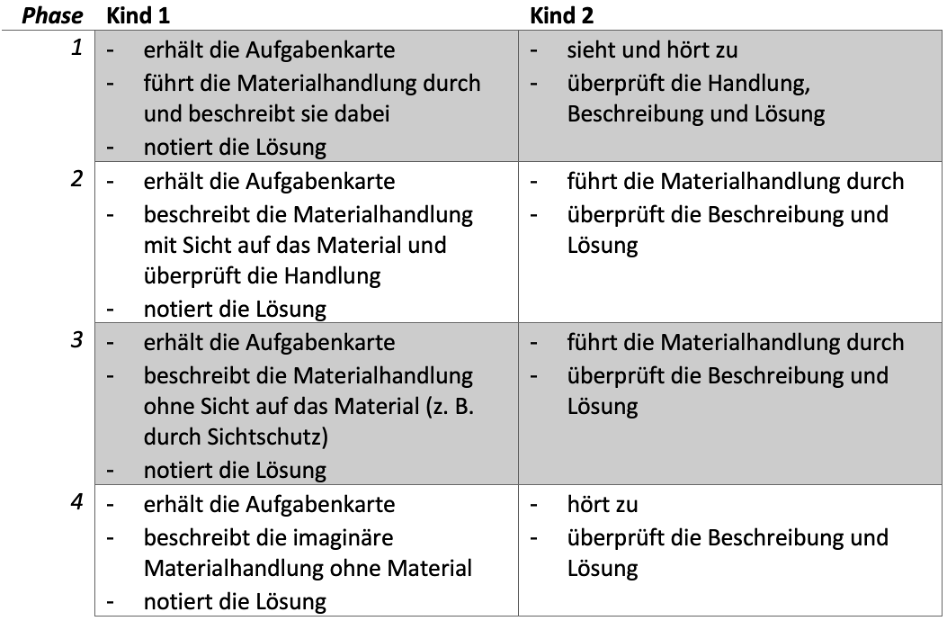 Tabelle 1: Materialhandlung in 4 Phasen beschreiben und verinnerlichen
Tabelle 1: Materialhandlung in 4 Phasen beschreiben und verinnerlichen
Der Ablauf der möglichen Basisaktivität orientiert sich am Vierphasenmodell (vgl. Wartha & Schulz 2011, S. 11), das im Modul Diagnose-/ Fördergespräche weiter erläutert wird. Es eignet sich dazu, den Übergang von konkreten Materialhandlungen zu gedanklichen Operationen zu fördern. Somit werden hier die Materialhandlung zum Stellenweisen Abziehen mit Entbündeln in der durch den Algorithmus vorgegebenen Reihenfolge verinnerlicht und durch den Darstellungswechsel zur sprachlich-symbolischen Darstellungsform eine Grundvorstellung zum Algorithmus aufgebaut. Zur Unterstützung des Beschreibens kann ein Wortspeicher gemeinsam angelegt und genutzt werden (siehe Möglichkeiten individueller Unterstützung). So wird von den individuellen Versprachlichungen der Kinder ausgehend eine Fachsprache entwickelt und genutzt.
Basisaktivität
Von der Materialhandlung zur bildlichen Darstellungsform
Material: Aufgabenkarte, Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen), Karten (bildliche Darstellung)
Die Kinder erhalten eine Aufgabenkarte der Basisaufgabe und Karten, auf denen die Rechenschritte der Aufgabe bildlich dargestellt sind. Sie sollen die einzelnen Schritte des Rechenweges mit Material legen und die jeweils passenden bildlichen Darstellungen zuordnen. Dies kann gut in einer Partnerarbeit erfolgen, da die Kinder so gemeinsam über die Rechenschritte kommunizieren und sich bei der Materialhandlung abwechseln und unterstützen können.
Aufgabenstellung: „Legt Schritt für Schritt mit Material. Ordnet jedem Schritt ein passendes Bild zu. Beschreibt.“
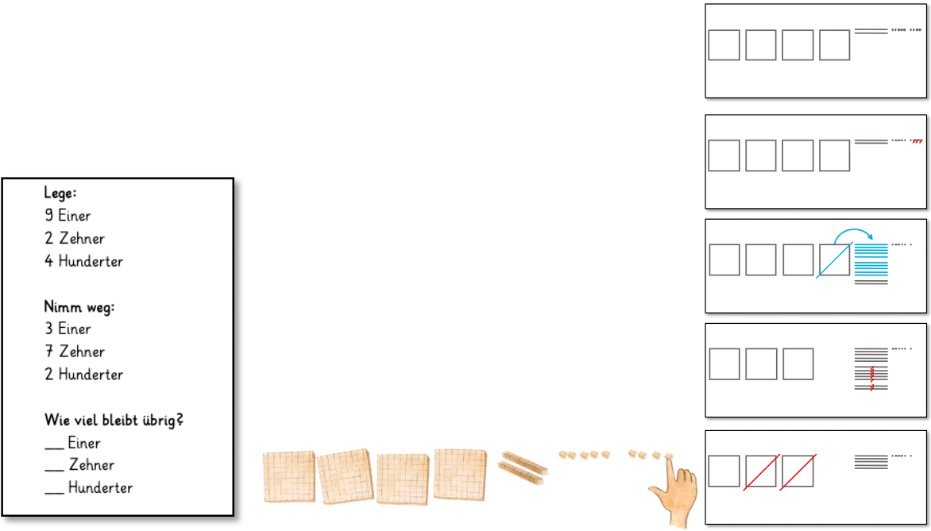 Abbildung 3: Zuordnen der bildlichen Darstellung (Karten rechts) zur Materialhandlung
Abbildung 3: Zuordnen der bildlichen Darstellung (Karten rechts) zur Materialhandlung
Die bildliche Darstellung ist gekennzeichnet durch verschiedene Zeichen, mit unterschiedlichen Bedeutungen, die die Kinder erfassen und versprachlichen müssen. Die Zahldarstellung erfolgt beispielsweise durch Quadrate als Hunderter, Striche als Zehner und Punkte als Einer. Des Weiteren bedeutet das rote Durchstreichen hier, dass die Menge weggenommen wird, während der Pfeil in Kombination mit den blauen Markierungen ein Zeichen für das Entbündeln eines Hunderters in zehn Zehner darstellt. Die Bedeutung des Zeichens für das Entbündeln kann gemeinsam festgelegt und dem Wortspeicher als Bildzeichen hinzugefügt werden. Um die Zeichen zu interpretieren, sollen die Kinder an die bereits bekannte Materialhandlung anknüpfen und so beide Darstellungsformen vernetzen.
Grundsätzlich ist es auch möglich, dass die Kinder an einer anderen Stelle Material wegnehmen oder entbündeln, als es auf den Karten abgebildet ist. So können beispielsweise auch die drei Einer von links weggenommen werden. Durch Impulse wie „Welche Einer / Zehner / Hunderter habt ihr weggenommen / entbündelt? Hättet ihr auch andere Einer / Zehner / Hunderter wegnehmen / entbündeln können? Wie ist es im Bild?“ wird ein Austausch über geschickte Materialhandlungen und Rechenstrategien angeregt.
Basisaktivität
Von der bildlichen zur mathematisch-symbolischen Darstellungsform
Material: Streifen (bildliche Darstellung), Karten (mathematisch-symbolische Darstellung)
Nachdem die Kinder die bildliche Darstellung interpretiert und beschrieben haben, sollen sie nun die mathematisch-symbolische Darstellung zum jeweils passenden Rechenschritt der bildlichen Darstellung zuordnen und ihre Zuordnung beschreiben.
Diese mögliche Basisaktivität ist besonders herausfordernd, wenn im Vorfeld die Notationsschritte des schriftlichen Verfahrens noch nicht gemeinsam erarbeitet wurden, weil die Kinder die Zusammenhänge zwischen den beiden Darstellungsarten selbstständig finden und untersuchen sollen. In diesem Zusammenhang kann die Lehrkraft überlegen, ob sie mit einzelnen Kindern die Notation des schriftlichen Verfahrens vorher an einem Beispiel anschauungsgestützt entwickelt. Hierzu können gut die Schülerdokumente aus der Basisaufgabe und der zweiten Basisaktivität genutzt werden.
Aufgabenstellung: „Zu jedem Rechenschritt im Bild passt eine Rechnung. Ordne zu. Beschreibe.“
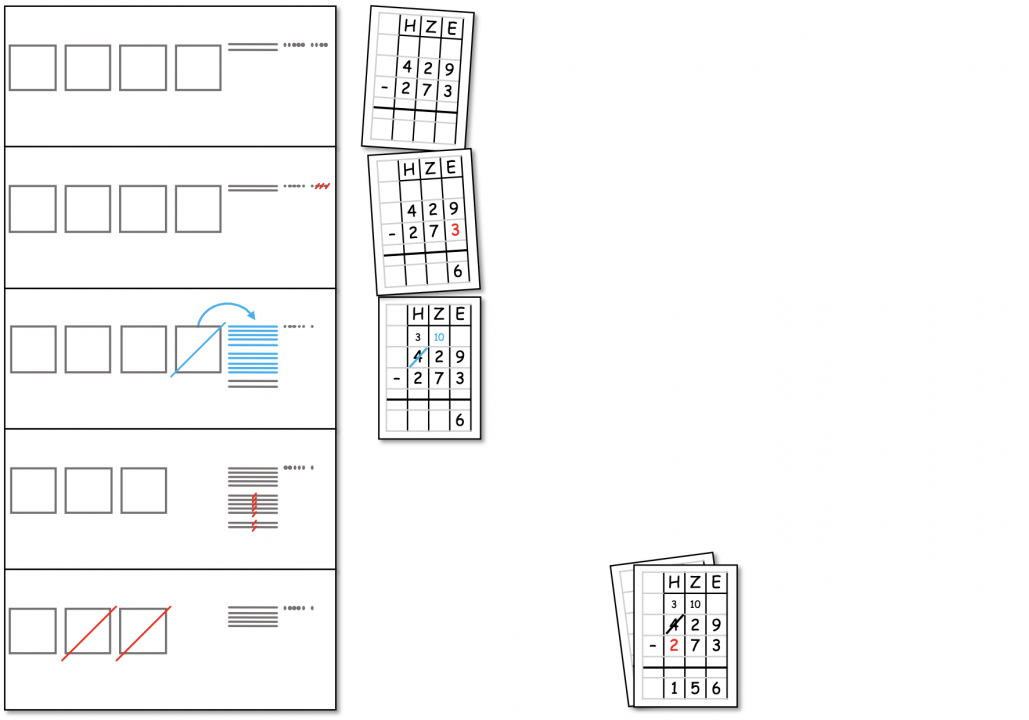 Abbildung 4: Zuordnen der mathematisch-symbolischen (Karten rechts) zur bildlichen Darstellung (Streifen links)
Abbildung 4: Zuordnen der mathematisch-symbolischen (Karten rechts) zur bildlichen Darstellung (Streifen links)
Die symbolische Darstellung folgt ebenfalls festgelegten Konventionen (Notationsform untereinander, stellengerechte Zerlegung und Verrechnung der Zahlen, Rechenrichtung, Notationsform des Entbündelns …), die die Kinder zunächst interpretieren müssen. Dazu können sie auf ihre Vorerfahrungen durch die Materialhandlung und bildliche Darstellung desselben Rechenweges zurückgreifen und sich durch den Darstellungswechsel z. B. die Notationsform des Entbündelns erschließen. Auch auf die Vorerfahrungen mit der Notation der schriftlichen Addition kann hier zurückgegriffen werden.
Durch Impulse wie „Warum passen Bild und Rechnung zueinander? Wo sieht man … im Bild? Wo sieht man … in der Rechnung?“ kann der Fokus auf einzelne Rechenschritte angeregt werden. Zur Unterstützung des Beschreibens kann wiederum der gemeinsame Wortspeicher (siehe Möglichkeiten individueller Unterstützung) genutzt werden.
Basisaktivität
Von der mathematisch-symbolischen Darstellungsform zur Materialhandlung
Material: Streifen (mathematisch-symbolische Darstellung), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
Die Kinder erhalten einen Streifen einer Aufgabe in mathematisch-symbolischer Darstellungsform, legen die Aufgabe mit Material nach und beschreiben die Passung zwischen Rechnung und Handlung.
Aufgabenstellung: „Lege jeden Rechenschritt mit Material. Beschreibe.“
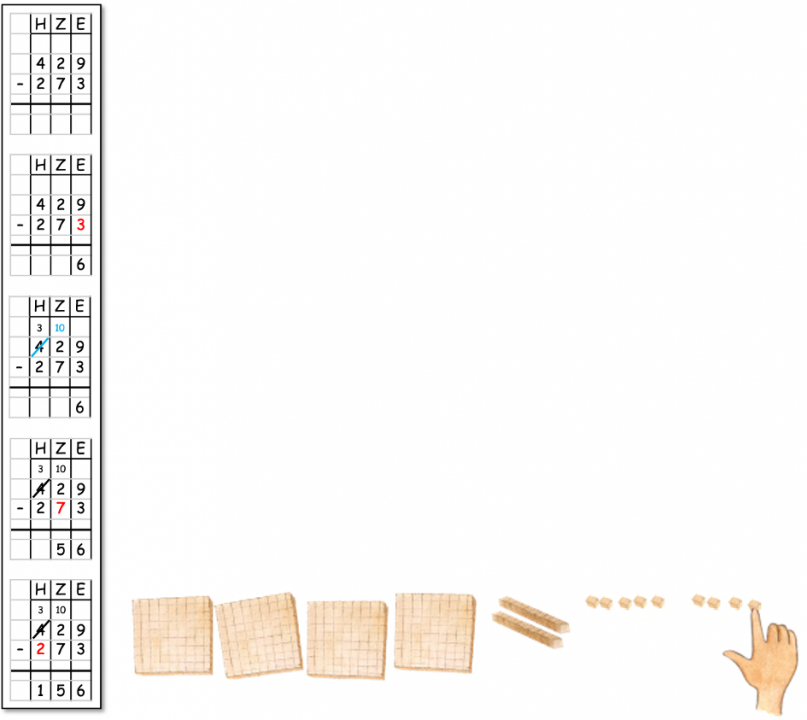 Abbildung 5: Materialhandlung zu mathematisch-symbolischer Darstellung legen und beschreiben
Abbildung 5: Materialhandlung zu mathematisch-symbolischer Darstellung legen und beschreiben
Durch Impulse wie „Warum passen Rechnung und Material zueinander? Wo sieht man … am Material? Wo sieht man … in der Rechnung?“ kann der Fokus auf einzelne Rechenschritte angeregt werden.
Basisaktivität
Verknüpfen verschiedener Darstellungen des gleichen Rechenschrittes
Material: Vorlage zum Ordnen, Karten (bildliche, mathematisch- und sprachlich-symbolische Darstellung Iven & Lea)
Die Kinder erhalten Karten des gleichen Rechenschrittes verschiedener Aufgaben in den vier verschiedenen Darstellungsformen. Die Beschreibung von Iven orientiert sich eher an der Materialhandlung. Die Beschreibung von Lea entspricht eher der Rechnung. Die Kinder sollen immer vier Karten des gleichen Rechenschrittes einer Aufgabe den unterschiedlichen Darstellungsformen auf der Vorlage zuordnen und ihre Zuordnung begründen.
Aufgabenstellung: „Immer ein Bild, eine Rechnung, eine Beschreibung von Iven und eine Beschreibung von Lea passen zusammen. Ordne zu und begründe.“
 Abbildung 6: Vorlage zum Ordnen mit Karten in bildlicher, mathematisch- und sprachlich-symbolischer Darstellung
Abbildung 6: Vorlage zum Ordnen mit Karten in bildlicher, mathematisch- und sprachlich-symbolischer Darstellung
Durch die Aufgabenstellung werden gezielt Darstellungswechsel zwischen Bildern, mathematischen und sprachlichen Symbolen angeregt und fokussiert. Dabei kann die Anzahl der Karten, die den Kindern zur Verfügung gestellt wird, variieren. So können zum Beispiel auch nur Bild und Rechnung einander zugeordnet werden. Mithilfe der Impulse „Was ist bei den Rechenschritten gleich? Was ist verschieden?“ können die Kinder Gemeinsamkeiten und Unterschiede zwischen den Darstellungsformen erkunden.
Reduktion
Fokussieren auf stellengerechtes Wegnehmen
Material: Aufgabenkarten, Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
Die Kinder erhalten ausschließlich Aufgabenkarten der Basisaufgabe, bei denen kein Entbündeln erforderlich ist. So wird der Fokus zunächst auf das Stellengerechte Abziehen in Verbindung mit dem Operations- und Stellenwertverständnis gelegt. Auch leistungsschwächere Kinder können somit „Expert:innen für Wegnehmschritte“ in Phasen des gemeinsamen Austausches sein.
 Abbildung 7: Aufgabenkarte Fokussieren auf stellengerechtes Wegnehmen
Abbildung 7: Aufgabenkarte Fokussieren auf stellengerechtes Wegnehmen
Reduktion
Fokussieren auf Entbündelungsaktivitäten
Material: Aufgabenkarten, Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
Die Kinder erhalten Aufgabenkarten, die sie wie bei der Basisaufgabe mit Legematerial lösen sollen. Hierbei liegt der Fokus auf Entbündelungsaktivitäten, während das stellengerechte Abziehen mehrerer Stellenwerte und die Reihenfolge des Algorithmus zunächst keine Rolle spielen. Hier werden die Kinder also zu „Expert:innen für Entbündelungsschritte“.
Aufgabenstellung: „Lege mit Material und nimm weg. Wie kannst du tauschen, damit du die Aufgabe lösen kannst? Wie viel bleibt übrig?“
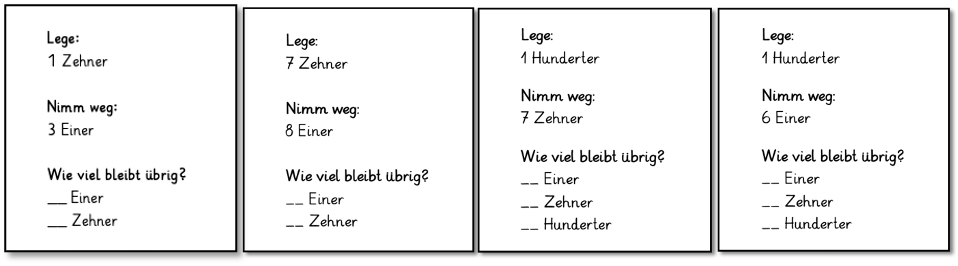 Abbildung 8: Aufgabenkarten Fokussieren auf Entbündelungsaktivitäten
Abbildung 8: Aufgabenkarten Fokussieren auf Entbündelungsaktivitäten
Reduktion
Fokussieren auf zweistellige Zahlen
Die Basisaufgaben und mögliche Basisaktivitäten können in ihrer Komplexität durch ein Fokussieren auf zweistellige Zahlen reduziert werden, womit sich die Anzahl der Rechenschritte verringert. Die Aufgabenstellungen bleiben unverändert – lediglich das Material und der Zahlenraum ändern sich.
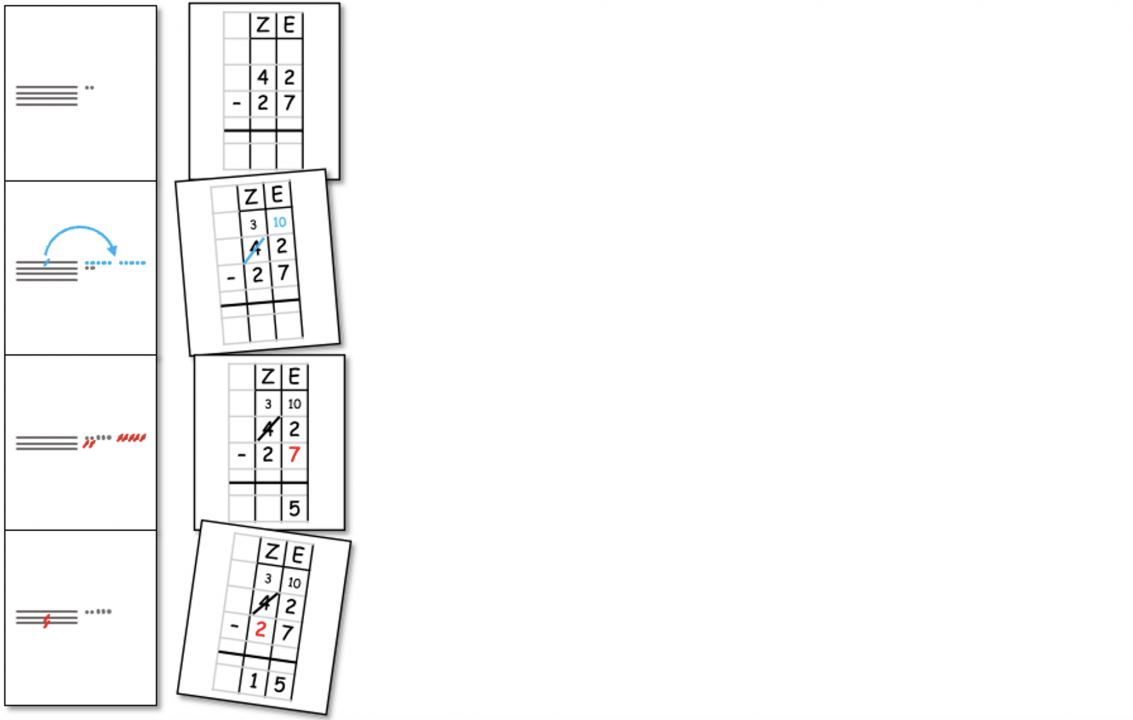 Abbildung 9: Bildliche und mathematisch-symbolische Darstellung der Rechenschritte einer Aufgabe mit zweistelligen Zahlen und einer Entbündelung
Abbildung 9: Bildliche und mathematisch-symbolische Darstellung der Rechenschritte einer Aufgabe mit zweistelligen Zahlen und einer Entbündelung
In der Basisaufgabe sind Aufgabenkarten mit Entbündelung an unterschiedlichen Stellenwerten enthalten. Die Zahlen dieser Reduktionsaufgabe sind so gewählt, dass es zu jeder Basisaufgaben eine passende Reduktionsaufgabe gibt. So wird ein Arbeiten und Reflektieren am gemeinsamen Lerngegenstand und ein Herstellen von Bezügen zwischen den Aufgaben ermöglicht. Je nach Stellenwert der Entbündelung in der Basisaufgabe unterscheidet sich jedoch die Art der Beziehung:
-
Komplexere Beziehung:
Die Ziffern der Basisaufgabe verschieben sich bei der Reduktionsaufgabe um einen Stellenwert nach hinten. Die Entbündelung findet so auch an unterschiedlichen Stellenwerten statt (Bsp. Basisaufgabe 429 – 273; Reduktionsaufgabe 42 – 27).
-
Einfachere Beziehung:
Die Basis- und Reduktionsaufgaben haben gleiche Zehner und Einer. In beiden Fällen wird ein Zehner in zehn Einer entbündelt (Bsp. Basisaufgabe 563 – 227; Reduktionsaufgabe 63 – 27).
Durch eine explizite Thematisierung kann das Stellenwertverständnis durch die Aufgabenstellung „Vergleiche die Bilder und Stellenwerttafeln der beiden Aufgaben. Was ist gleich, was ist verschieden?“ vertieft werden.
Das Aufgabenmaterial sollte in Abhängigkeit von den individuellen Lernvoraussetzungen der Schüler:innen ausgewählt werden. So kann beeinflusst werden, welche Arten von Beziehungen zwischen Basis- und Reduktionsaufgabe in einer gemeinsamen Reflexion thematisiert werden können. Falls nur eine der beiden Beziehungen angesprochen werden soll, müssen die jeweils anderen Aufgabenkarten der Basis- und Reduktionsaufgabe vorher aussortiert werden.
Erweiterung
Aufgaben mit mehreren Entbündelungen oder Nullen im Minuenden
Material: Aufgabenkarten, Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
Die Kinder bearbeiten die Aufgabenstellung der Basisaufgabe: „Lege mit Material und nimm weg: Einer, Zehner und Hunderter. Wie viel bleibt übrig?“. Mithilfe der vorgegebenen Karten wird jedoch die Aufgabenschwierigkeit dadurch erhöht, dass zwei Entbündelungen vorgenommen werden müssen bzw. Nullen im Minuenden vorhanden sind.
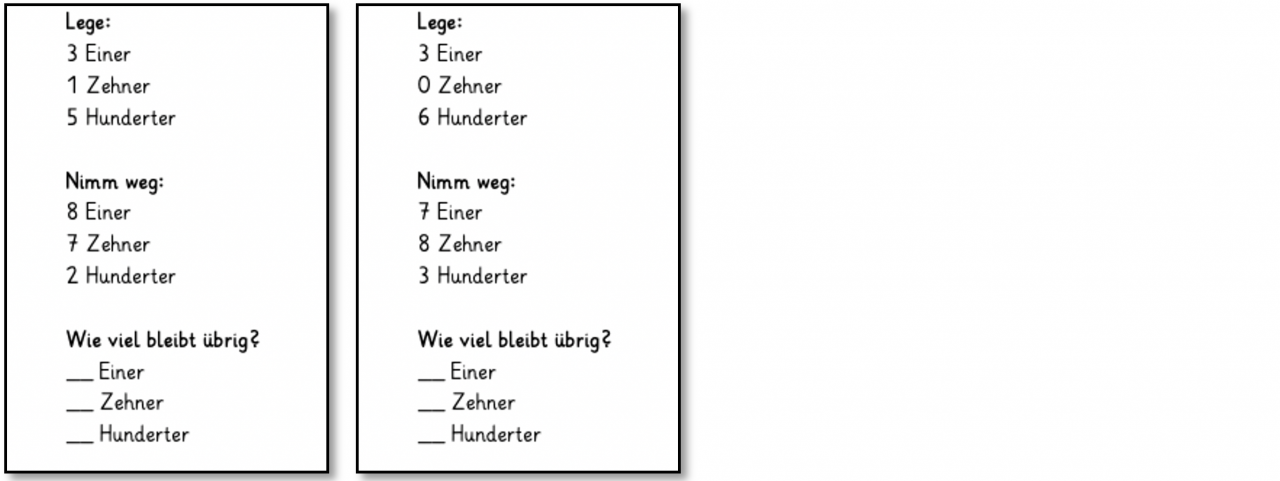 Abbildung 10: Beispiel für Aufgabenkarten mit zwei Entbündelungen und Null im Minuenden
Abbildung 10: Beispiel für Aufgabenkarten mit zwei Entbündelungen und Null im Minuenden
Das Vorhandensein von Nullen im Minuenden kann bei dem Entbündeln eine Schwierigkeit darstellen: Wenn ein Stellenwert mit einer Null besetzt ist, kann dieser nicht entbündelt werden. Es muss also auf den nächstmöglichen Stellenwert vorgegriffen werden, dessen Entbündelung dann jeweils wiederum weiter entbündelt wird, bis der Minuend an dem Ausgangsstellenwert wieder größer als der Subtrahend ist. Dieses Vorgehen kann von den Kindern gut am Material entdeckt und handelnd durchgeführt werden.
Erweiterung
Ordnen der Rechenschritte
Material: Karten (bildliche / mathematisch-symbolische Darstellung)
Die Kinder erhalten Karten mit bildlicher und / oder mathematisch-symbolischer Darstellung der Rechenschritte einer Aufgabe, die sie in eine Reihenfolge bringen und erklären müssen.
Aufgabenstellung: „Bringe die Rechenschritte in die richtige Reihenfolge. Erkläre.“
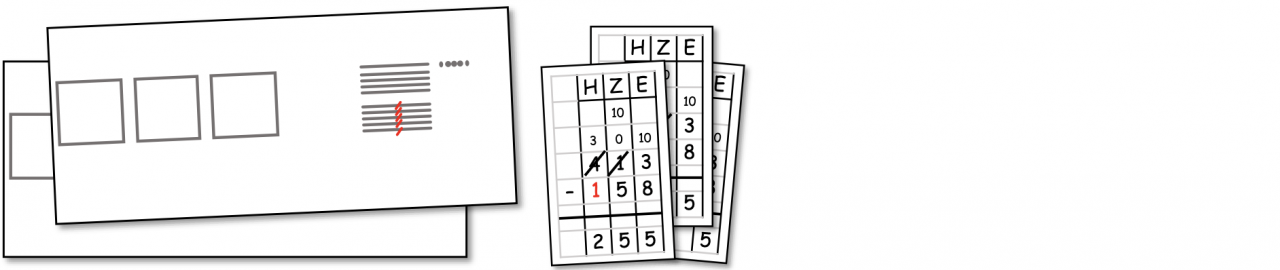 Abbildung 11: Ordnen der bildlichen / mathematisch-symbolischen Darstellung der Rechenschritte
Abbildung 11: Ordnen der bildlichen / mathematisch-symbolischen Darstellung der Rechenschritte
In den Karten sind auch Aufgaben mit zwei Entbündelungen und Nullen im Minuenden enthalten. Dadurch erschließen sich die Kinder auch, in welcher Reihenfolge und wie die Entbündelungen bei diesen komplexeren Aufgabenstellungen symbolisch notiert werden.
Als weitergehende Aufgabenstellung können die Kinder auch angeregt werden, immer ein Bild und eine Rechnung einander zuzuordnen und zu begründen, warum diese zusammenpassen. Dadurch wird der Wechsel zwischen bildlicher, mathematisch- und sprachlich-symbolischer Darstellungsform weiter vertieft.
Erweiterung
Erfinden und schriftliches Lösen eigener Aufgaben
Material: Heft
Bei dieser offenen Aufgabenstellung denken sich die Kinder selbst Aufgaben aus, die sie schriftlich lösen. Dabei können sie sich an der mathematisch-symbolischen Darstellungsform aus den vorherigen Aufgaben orientieren. Durch eine Einschränkung in Form einer vorgegebenen Anzahl an Entbündelungen kann der Blick auf die Zahlbeziehungen gefördert werden. Als Möglichkeit individueller Unterstützung eignet sich auch hier das Legematerial.
Aufgabenstellung: „Denke dir selbst Minusaufgaben (mit 0 / 1 / 2 / … Entbündelungen) aus und löse sie schriftlich wie Lea.“
Erweiterung
Beschreiben und Verinnerlichen der Materialhandlung II
Material: Karten (mathematisch-symbolische Darstellung), Legematerial (Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen)
In dieser Aufgabenstellung durchlaufen die Kinder in Partnerarbeit wie in der möglichen Basisaktivität das Vierphasenmodell (siehe Beschreiben und Verinnerlichen der Materialhandlung). Statt der Aufgabenkarten der Basisaufgabe erhält Kind 1 jedoch eine Aufgabe in mathematisch-symbolischer Darstellungsform, die es löst und zu jedem Rechenschritt die passende Materialhandlung beschreibt.
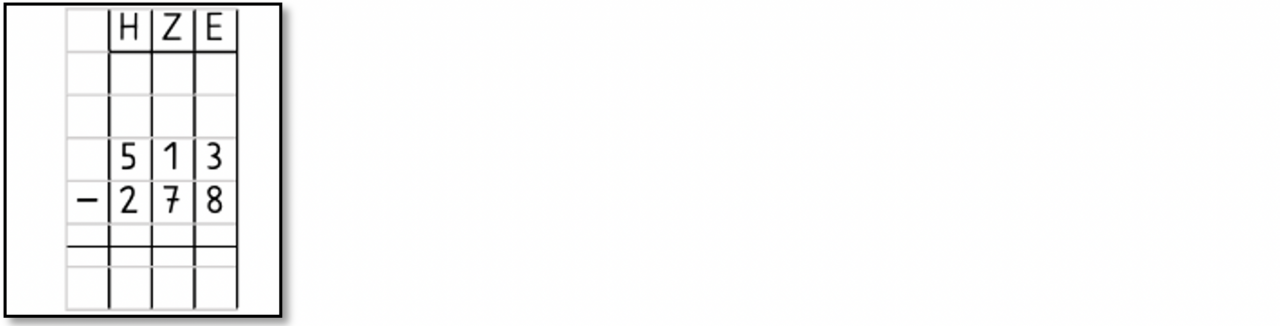 Abbildung 12: Karte (mathematisch-symbolische Darstellung)
Abbildung 12: Karte (mathematisch-symbolische Darstellung)
Möglichkeiten individueller Unterstützung
Material nutzen
Haben die Kinder Schwierigkeiten, die bildliche oder mathematisch-symbolische Darstellung nachzuvollziehen oder selbst zu entwickeln, können sie diese mit Legematerial legen. Dadurch wird der Darstellungswechsel unterstützt.
Möglichkeiten individueller Unterstützung
Lupe
Durch Auflegen und Verschieben einer Folie / „Lupe“ kann ein einzelner Rechenschritt oder ein Stellenwert fokussiert werden.
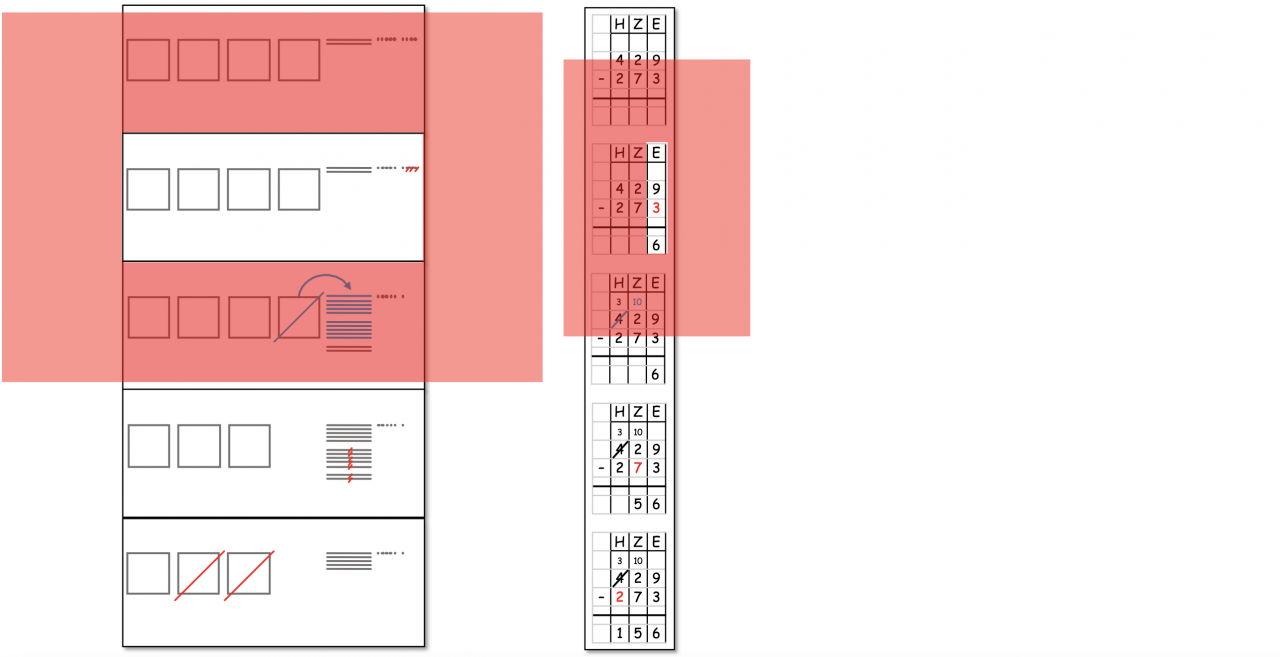 Abbildung 13: Fokussierung eines Rechenschrittes (links) oder Stellenwertes (rechts) mithilfe einer „Lupe“
Abbildung 13: Fokussierung eines Rechenschrittes (links) oder Stellenwertes (rechts) mithilfe einer „Lupe“
Möglichkeiten individueller Unterstützung
Einen Wortspeicher anlegen und Sprachmuster verwenden
Das Beschreiben der Rechenwege kann durch die das Anlegen eines Wortspeichers und die Vorgabe von Satzbausteinen unterstützt werden (vgl. hierzu auch Förderschwerpunkte: Sprache: Unterricht). Die zentralen Fachwörter und Sprachmuster sind in folgendem Wortspeicher visualisiert, wobei den Artikeln der, die und dasgemäß des DemeK-Konzeptes (vgl. Bezirksregierung Köln 2012) jeweils die Farben blau, rot und grün zugeordnet werden.
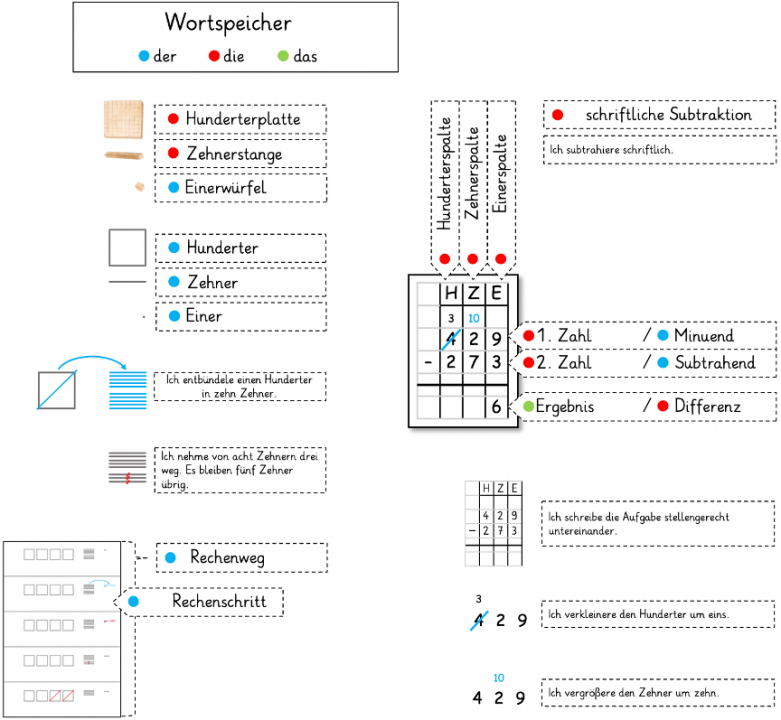 Abbildung 14: Wortspeicher mit Visualisierung der zentralen Fachwörter und Sprachmuster der Aufgabenstellung kompakt
Abbildung 14: Wortspeicher mit Visualisierung der zentralen Fachwörter und Sprachmuster der Aufgabenstellung kompakt
Zusätzlich zum Wortspeicher können sprachschwächere Kinder bei der Beschreibung der Rechenschritte durch vorgegebene Satzbausteine unterstützt werden. Diese sind auf Karten abgebildet, so dass jeder Rechenschritt des Subtraktionsalgorithmus durch eine Karte beschrieben wird. Die Karten können flexibel zu den möglichen Basisaktivitäten, Reduktions- und Erweiterungsaufgaben genutzt und den anderen Darstellungsformen zugeordnet werden. Dabei müssen die Kinder die passende Karte heraussuchen und die konkreten Zahlwerte ergänzen.
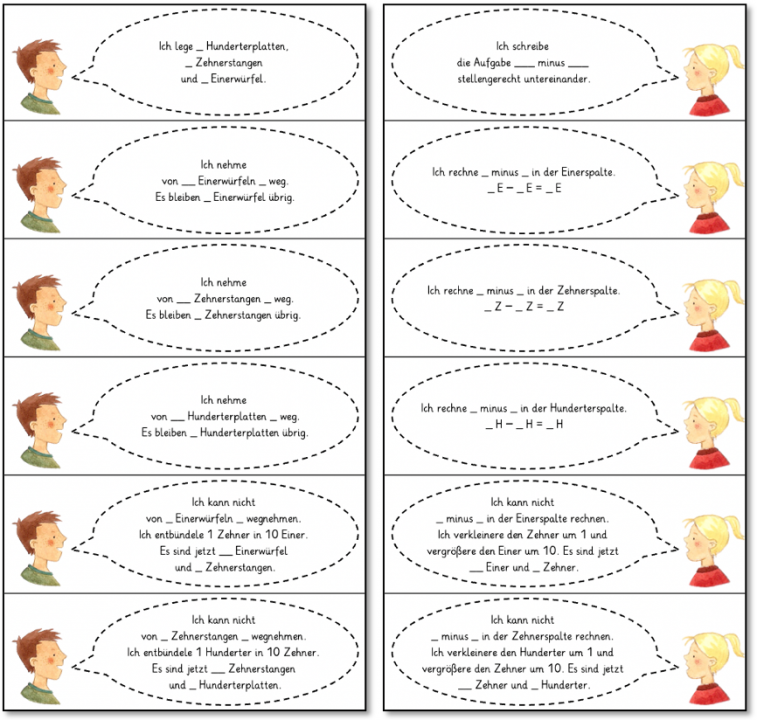 Abbildung 15: Karten mit Satzbausteinen zur Beschreibung der Materialhandlung (links) und der mathematisch-symbolischen Notation (rechts)
Abbildung 15: Karten mit Satzbausteinen zur Beschreibung der Materialhandlung (links) und der mathematisch-symbolischen Notation (rechts)