Kinder mit dem Förderschwerpunkt Sehen können grundsätzlich Mathematik auf gleichem Niveau lernen wie Kinder ohne Förderbedarf. Es gibt einige erfolgreiche Mathematiker mit einer Sehschädigung (Jackson, 2002). Da Mathematikunterricht aber (auch jenseits von Geometrie) üblicherweise stark Bezug nimmt auf visuelle Darstellungen und Veranschaulichungen, gibt es einiges zu beachten. Zum einen stellt sich immer wieder die Frage nach zugänglichen Materialien und nach optischen und elektronischen Hilfsmitteln für den Unterricht, zum anderen entwickeln diese Kinder teilweise unerwartete Strategien beim Mathematiklernen und müssen mathematische Lernhürden überwinden, die für andere Kinder weniger ins Gewicht fallen. Dies soll hier an zwei Beispielen verdeutlicht werden:
Beispiel 1:
In einer inklusiven, jahrgangsübergreifenden Klasse soll die Orientierung am Zwanzigerfeld (1. Klasse) bzw. Hunderterfeld thematisiert werden. Dafür hat die Lehrerin Material von PIKAS ausgewählt:
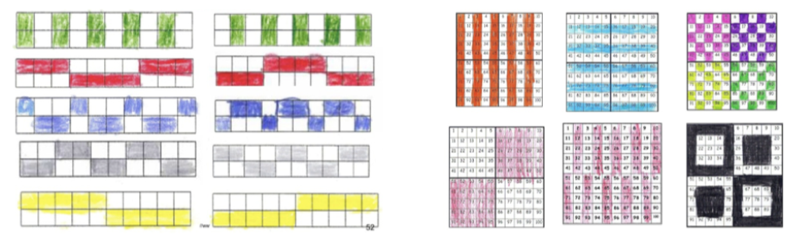Abbildung 1: Die Hälfte färben am Zwanzigerfeld und am Hunderterfeld
In der Klasse befindet sich auch Merve, eine blinde Erstklässlerin. Die Klassenlehrerin überlegt daher zusammen mit einer Sonderpädagogin der Förderschule Sehen, wie dies umsetzbar sein könnte.
Haben Sie Ideen? Mögliche Ansätze für die Unterrichtsgestaltung finden sich im Teilmodul „Unterricht“.
Beispiel 2:
Manche Kinder entwickeln aufgrund des anderen Zugangs zu Mathematik auch besondere Strategien, wie z.B. Martón (8 Jahre alt):
I: Wenn der Bäcker 24 Brötchen backt und es sind 6 übrig, wie viele hat der Dieb geklaut?
M: … 18.
I: Woher weißt du das?
M: Einzeln.
I: Zeig es mir bitte.
M: 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.
I: Woher weißt du, dass das 18 Zahlen sind?
M: In meinem Kopf.
(...)
I: Wenn dort 9 Brötchen waren und er Bäcker findet nur 5 davon, wie viele sind geklaut worden?
M: 4.
I: Woher weißt du das?
M: 9-4.
I: Ich habe dir die 4 nicht genannt.
M: Aber er fand 5.
I: Aber woher weißt du, dass du 4 subtrahieren musst?
M: …
I: Es waren 9 und es sind 5 übrig. Hast du subtrahiert oder addiert?
M: …
I: Versuch es!
M: Ich sage es mir selbst: 8, 7, 6, 5.
(Ahlberg & Csocsán, 1997)
Wie geht Martón beim Rechnen vor? Im Teilmodul „Hintergrund“ wird das Interview mit dem Schüler erneut aufgegriffen und seine Zählstrategien werden eingehender erläutert.
