Blinde und sehbeeinträchtigte Lernende werden in der Regel zielgleich unterrichtet, folgen also dem Bildungsplan der Grundschule. Veränderungen ergeben sich eher bezüglich der Unterrichtsgestaltung und der Materialien.
Lehrkräfte und Mitschüler müssen ihr Verhalten in der unterrichtlichen Kommunikation anpassen, z.B. bezüglich Zeigegesten und ungenauen Ortsangaben („da drüben“). Für den Umgang mit dem Tafelbild stehen bei Sehbehinderung Hilfsmittel zur Verfügung (z.B. eine Tafelkamera, vgl. dazu Teilmodul „Vertiefende Informationen – Medien, Hilfsmittel und Unterrichtsprinzipien – Unterricht bei Sehbeeinträchtigung“), eventuell gibt es auch eine Schulbegleitung (z.B. BuFDi) oder eine Sonderpädagogin, die unterstützen kann. Eine andere Möglichkeit ist, das Tafelbild vorweg zu planen und es den Lernenden nach Bedarf taktil oder visuell (z.B. vergrößert) zur Verfügung zu stellen.
Lehrkräfte sollten nicht davon ausgehen oder erwarten, dass die Lernenden mit Förderschwerpunkt Sehen von sich aus nachfragen, wenn sie etwas nicht mitbekommen. Dies widerspricht dem Hierarchiegefälle zwischen Lehrkraft und Lernenden. Die Sicherstellung der Zugänglichkeit ist Aufgabe der Lehrkräfte.
Da sich für blinde und sehbeeinträchtigte Lernende z.T. spezifische Lernhürden und Risiken für die Entwicklung von Lernschwierigkeiten ergeben, wie im Teilmodul „Hintergrund“ dargestellt, ist es besonders wichtig, immer wieder diagnostische Elemente in den Unterricht einzubinden. Dies ist meist Aufgabe der Mathematiklehrkraft, selbst wenn sie von einer sonderpädagogisch ausgebildeten Lehrkraft unterstützt wird, denn diese Beratungslehrkräfte haben nicht immer auch eine mathematikdidaktische Ausbildung. Anregungen finden Sie auf dieser Webseite unter der Leitidee "Diagnosegeleitet fördern" und im Partnerpojekt KIRA.
In vielen Situationen brauchen Lernende mit Förderschwerpunkt Sehen mehr Zeit für die Bearbeitung von Aufgaben, da z.B. der Umgang mit Hilfsmitteln (vgl. Teilmodul „Vertiefende Informationen – Medien, Hilfsmittel und Unterrichtsprinzipien"), das Lesen, das Erfassen von Bildern, das Schreiben und Zeichnen und die Organisation der Materialien aufwändiger sind. Dies lässt sich auf unterschiedliche Weise auffangen, abhängig von der Unterrichtssituation:
-
Unterstützung durch Lehrkraft, Schulbegleitung oder Mitschüler/in
-
Ermöglichen von zeitlichem Vorlauf
-
Differenzierende Aufgabenstellungen, die für alle Kinder in der Klasse ein eigenes Lerntempo zulassen
-
Didaktisch sinnvolle Reduktion der zu bearbeitenden Aufgaben, Weglassen von Teilaufgaben (z.B. Zeichnen)
Bei den Materialien lässt sich als Faustregel festhalten, an Stelle von Bildern möglichst oft auf authentische, also echte Gegenstände zurückzugreifen. Mit Blick auf konkrete Unterrichtssituationen ergeben sich aber schnell Detailfragen, die so pauschal nicht zu klären sind. Am Beispiel aus dem Teilmodul „Einstieg“ soll dies hier erläutert werden.
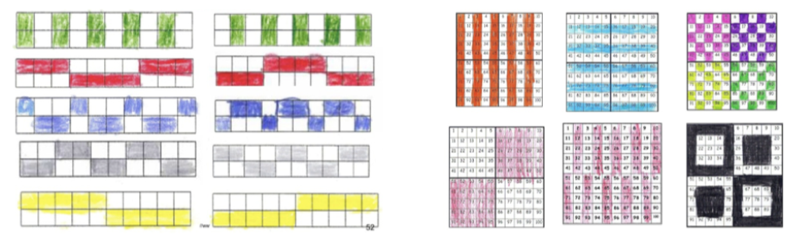Abbildung 1: Die Hälfte färben am Zwanzigerfeld und am Hunderterfeld
In einer jahrgangsgemischten, inklusiven Klasse (1. und 2. Schuljahr) sollen die Kinder am Zwanziger- bzw. Hunderterfeld Muster erzeugen, indem sie immer genau die Hälfte der Felder einfärben. Wie kann dieses Material gestaltet werden, so dass auch Merve, eine blinde Erstklässlerin, mitarbeiten kann?
Diese Frage ist auch deshalb so herausfordernd, weil es nicht nur darum geht, das Material für Merve zugänglich zu machen. Sie sollte sich im besten Fall auch mit den Mitschülern über ihre Ergebnisse und deren Ergebnisse austauschen können. Selbstverständlich darf aber auch die mathematische Zielstellung nicht aus dem Blick geraten: Merve soll ja weitgehend dasselbe lernen wie die anderen. Daraus ergibt sich ein komplexes Gemenge von Anforderungen an Material und Aufgabenstellung, das am besten mit Hilfe eines Planungsmodells in den Griff zu bekommen ist. Ein solches Modell sollte flexibel genug sein, um in vielen Planungssituationen eingesetzt zu werden, es sollte aber auch aufgrund seiner Struktur die Entscheidungsprozesse der Lehrkraft (oder des Planungsteams) systematisieren.
Ausgangspunkt sind, wie so oft bei der Unterrichtsplanung, die Lernziele.
Schritt 1: Lernziele
Welche mathematischen Kompetenzen sollen die Lernenden entwickeln?
Mathematische Lernziele bei dieser Aufgabenstellung könnten sein:
-
Orientierung auf dem Zwanzigerfeld (1. Klasse) und Hunderterfeld (2. Klasse)
-
Entwicklung eines flexiblen Verständnisses des Begriffs „Hälfte“
-
Erleben der symmetrischen Ästhetik
Auf der Basis dieser Festlegung können erste Ideen für die Umsetzung entwickelt werden. Im Sinne eines Brainstormings ist es sinnvoll, zunächst auch anscheinend abseitige Ideen zuzulassen. Was wäre also denkbar?
a) Nutzen von Klett oder Magneten zum Abdecken von Feldern
b) Anmalen auf Zeichenfolie
Abbildung 2: Anmalen auf Zeichenfolie
c) Nutzen der Rechenschiffchen
d) Darstellung als Rhythmus: Zeilen nacheinander oder gleichzeitig mit unterschiedlichen Klängen vertonen
Transkript "Muster1"
Transkript "Muster2"
Transkript "Muster3"
Transkript "Muster4"
Transkript "Muster5"
Im zweiten Schritt ist es wichtig, sich über die Individuellen Bedingungen, die Merve mitbringt, Gedanken zu machen. Was sind ihre Stärken und Schwächen bezüglich dieser Aufgabenstellung?
Schritt 2: Individuelle Bedingungen und Lernvoraussetzungen
Welche speziellen Bedürfnisse müssen beachtet werden?
Auf welchen Stärken lässt sich aufbauen, welche Schwächen gilt es zu beachten?
-
Merve verliert noch hin und wieder die Orientierung auf dem Zwanziger- oder Hunderterfeld
-
Ihr Fokus liegt oft auf dem Ordinalzahlbegriff
-
Arbeitsorganisation muss noch geübt werden
-
Sie arbeitet gern mit anderen zusammen, hat zwei gute Freundinnen in der Klasse
Auf dieser Grundlage lassen sich die Ideen aus dem ersten Schritt neu bewerten und ergänzen.
Die Ideen a)-c) erfordern alle eine gute Orientierung auf dem Zwanzigerfeld. Wenn sie zum Einsatz kommen, sollte diese Orientierung zusätzlich gefördert werden, durch Übung passender Taststrategien im Vorlauf oder durch Unterstützung im Prozess, je nach Bedarf. Zu passenden Taststrategien gehört es dabei auch, die Fünfer- und Zehner-Struktur des Feldes zu nutzen: Man kann z.B. beim Rechenschiffchen 5 Felder beim Tasten überstreichen, ohne zu zählen, weil zwischen dem fünften und sechsten Feld eine Lücke ist. Das Nutzen entsprechender Taststrategien kann auch dazu beitragen, dass Merve nicht mehr so stark auf das Zählen und den Ordinalzahlbegriff fixiert ist. Die Vertrautheit mit den Rechenschiffchen erleichtert die Arbeitsorganisation.
Idee d), die Verwendung von Rhythmen, ist vom „üblichen“ Mathematikunterricht weiter entfernt und muss aus didaktischer Sicht genauer hinterfragt werden (s. auch Schritt 4). Hier geht es zunächst aber um die Frage, ob diese Form der Darstellung für Merve geeignet ist. Es gibt Hinweise darauf, dass Rhythmen und andere akustische Mengen (z.B. Glockenschläge) von blinden Menschen effektiver verarbeitet werden als von sehenden (Leuders, 2012, 2016). Wichtiger für Merve ist aber, dass akustische Mengen im Gegensatz zu taktilen Mengen vom Gehirn so weiterverarbeitet werden, dass ein annähernd simultaner Eindruck der Menge entsteht. Dies könnte den Aufbau des Kardinalzahlbegriffs unterstützen. Zudem ist das Tasten aufgrund der fehlenden Übersicht kognitiv fordernd und kann daher dem mathematischen Lernen im Wege stehen.
Schritt 3: Inklusive Eigenschaften des Materials
Können alle Lernenden mit demselben Material arbeiten?
Können die Lernenden miteinander über ihre Ergebnisse kommunizieren?
Die Beschäftigung mit der Aufgabenstellung in der Klasse lebt auch davon, dass die Ergebnisse der Kinder verglichen und von allen wertgeschätzt werden können. Dafür wäre es wichtig, dass Merve die Ergebnisse der sehenden Kinder wahrnehmen kann und umgekehrt. Für die Ideen a)-c) gilt, dass Merves Ergebnisse für die sehenden Kinder zugänglich sind. Merve selbst hat aber nur dann Zugang zu den Ergebnissen der anderen, wenn diese ebenfalls tastbare Materialien nutzen. Dies scheint bei Idee a) möglich, wenn entsprechend kostengünstige Varianten eingesetzt werden. Zeichenfolie steht in der Regel nicht der ganzen Klasse zur Verfügung, weil die Kosten zusammen mit den Zeichenbrettern zu hoch sind. Rechenschiffchen dagegen werden ja von allen eingesetzt. Unabhängig von der Wahl der taktilen Variante ist dann allerdings noch zu fragen, wie Merve möglichst schnell und effektiv auf die Ergebnisse anderer zugreifen kann. Vermutlich wird es notwendig sein, ihr eine Auswahl zum Tasten zu geben, und sie beim Erfassen der Muster zu unterstützen. Ein Überblick über alle Ergebnisse der Klasse wird für sie unterrichtlich eher nicht umsetzbar sein.
Rhythmen sind für Merve vermutlich schneller und leichter zu erfassen. Die Muster sind allerdings relativ komplex, so dass es für Merve, und insbesondere auch für die sehenden Kinder, durchaus herausfordernd ist, sie auditiv zu unterscheiden. Eventuell hat Merve hier sogar einen Vorteil.
Schritt 4: Didaktische Kriterien
Werden die zentralen mathematischen Inhalte durch das Material hervorgehoben?
Im letzten Schritt müssen die Adaptionsideen erneut daran gemessen werden, ob sie das Erreichen der Lernziele (Schritt 1) ermöglichen. Dies geschieht auf der Basis didaktischer Kriterien für das Fach Mathematik.
Die taktilen Varianten haben alle den Nachteil, dass das Ertasten der Muster relativ hohe kognitive Anforderungen stellt und viel Zeit in Anspruch nimmt. Dies kann den mathematischen Lernerfolg und die Kommunikation über die Ergebnisse beeinträchtigen. Es scheint also sinnvoll, die Rhythmus-Muster genauer zu untersuchen. Sie schneiden in Schritt 2 und 3 gut ab, aber aus didaktischer Sicht ergeben sich auch Fragen.
Die Produktion und die Erfassung der Rhythmen ist für Erst- und Zweitklässler relativ anspruchsvoll. Das bedeutet, dass entsprechend viel Zeit im Unterricht investiert werden muss, um dies zu üben. Es ist allerdings in einer Klasse mit einem blinden Kind sinnvoll, diese Form der Darstellung von Mengen und linearen Mustern häufiger einzusetzen, z.B. für die Zahldarstellung.
Musikalisches Rhythmusempfinden beruht meist auf einem Vierer- oder Dreiertakt (und ihren Vielfachen). Dies passt nicht zur Fünfer- und Zehnerstruktur des Dezimalsystems. Es erscheint nicht sinnvoll oder nachhaltig, mit Grundschulkindern einen Fünfertakt einzuüben. Man kann dies aber umgehen, wenn nach dem 5. Schlag eine Pause eingefügt wird. So entsteht ein wesentlich eingängigerer Sechsertakt, und die Fünferstruktur wird zusätzlich betont; zudem wird das Erzeugen oder Nachvollziehen der Rhythmen für die Kinder einfacher.
Transkript „Tonbeispiel 20er mit Fünferlücke“
Auditiv ist das Symmetrieempfinden anders als visuell. Da alles nacheinander abgespielt wird, sind achsensymmetrische Varianten weniger prägnant, Wiederholungen (also aus geometrischer Sicht Verschiebungen) stehen stärker im Fokus.
Praktisch gesehen ist es schwierig, wenn alle Kinder der Klasse gleichzeitig mit unterschiedlichen Rhythmen experimentieren. Es müssen also Möglichkeiten gefunden werden, dies im Unterrichtsverlauf zeitlich oder räumlich zu entzerren.
Akustische Eindrücke sind zudem flüchtig, d.h. sie müssen dokumentiert oder wieder abgespielt werden, um sie noch einmal zu erleben. Tonaufnahmen lassen sich zwar z.B. mit einem Smartphone leicht realisieren, dies ist aber nicht geeignet dafür, dass alle Kinder gleichzeitig ihre Ergebnisse aufzeichnen. Deshalb erscheint es sinnvoll, die akustischen Muster mit den visuellen / haptischen zu verknüpfen: die angemalten / nicht angemalten Felder können z.B. mit Klatschen und Klopfen verbunden werden und sind dann in beide Richtungen übersetzbar. So ist eine Dokumentation der Ergebnisse möglich, aber auch eine leichte Zugänglichkeit für Merve vorhanden. Das Übersetzen von einer Modalität in eine andere fördert zudem das Abstraktionsvermögen.
Abschließend könnte man zum folgenden Ergebnis kommen: In der Klasse werden akustische und visuelle/taktile Muster parallel eingesetzt. Alle Erstklässler arbeiten am Rechenschiffchen, alle Zweitklässler an der Hundertertafel. Die Kinder können selbst wählen, welchen Zugang sie bevorzugen, um Muster zu entwickeln und dann in die jeweils andere Darstellungsform zu übertragen. Bei den akustischen Mustern müssen allerdings die Regeln (Pause nach 5 und 10) vorher an Beispielen besprochen werden.
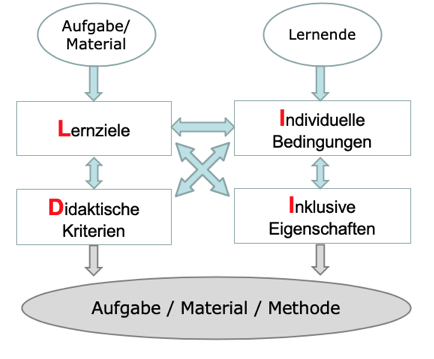Abbildung 3: LIID-Modell: Vier Schritte für die Entwicklung oder Auswahl von Materialien
Bei der Entwicklung oder Auswahl von Materialien erscheint es also sinnvoll, in vier Schritten vorzugehen (Leuders & Lang, im Druck), wie in Abbildung 5 gezeigt. Diese Schritte sind aber natürlich nicht unabhängig voneinander – z.B. kann sich aus Schritt 2 (Individuelle Bedingungen) ein spezifisches Lernziel (Schritt 1) ergeben, z.B. der Erwerb von Taststrategien. Nicht selten kommt es auch zu Gegensätzen: Ein Material, das aus Sicht von Schritt 2 (Individuelle Bedingungen) sehr gut passt, kann mit Blick auf die inklusiven Eigenschaften (Schritt 3) völlig ungeeignet sein. Das „LIID-Modell“ (gebildet aus den Anfangsbuchstaben der jeweiligen Schritte) dient hier als Instrument für die Planung Reflexion und stellt sicher, dass keine wichtigen Aspekte übersehen werden. Es kann die Abwägungen systematisieren, nimmt den Lehrkräften aber nicht die konkreten Entscheidungen ab.
