Aufgabenstellung kompakt
In der Aufgabenstellung kompakt zur schriftlichen Division werden zentrale Basiskompetenzen wie Ziffernrechnen, Stellenwertverständnis und Operationsverständnis am Übergang von der Primarstufe zur Sekundarstufe I aufgegriffen.
Bei der Förderung der Basiskompetenz Ziffernrechnen geht es darum, Algorithmen nachzuvollziehen und verständig zu nutzen. Durch die Anwendung eines Kartensets (s.u.) und der Arbeit mit Material mit der Stellentafel vollziehen die Kinder den schriftlichen Algorithmus handlungsorientiert und verstehensorientiert Schritt für Schritt nach. Dabei vertiefen sie das Operationsverständnis des Aufteilens als eine Grundvorstellung der Division. Sie verbinden den Begriff des Aufteilens mit einer konkreten Handlung, indem sie die Fragestellung „Wie viele Bündel entstehen?“ am Material durch die wiederholte Bündelung einer Plättchenmenge begleiten. Das Stellenwertverständnis wird durch das stellenweise Aufteilen und das Entbündeln der Reste gefördert und durch konkrete Handlungen mit Material an der Stellentafel.
Auf der Inhaltsebene steht ein materialgestützter, verstehensorientierter Zugang zum schriftlichen Divisionsalgorithmus im Vordergrund. Dieser Zugang wird durch ein schrittweises Erarbeiten des Verfahrens mithilfe des Kartensets ermöglicht. Auf der Prozessebene liegt der Schwerpunkt auf dem Vernetzen verschiedener Darstellungen, wodurch das Stellenwert- und Operationsverständnis im Bereich der Division nachhaltig gestärkt wird (MSB NRW, 2021, S. 86; MSB NRW, 2022, S. 27).

Die folgende Übersicht zeigt, welche Materialien für die Aufgabenstellungen benötigt werden. Unter „Material“ finden Sie zudem Kopiervorlagen. Diese beinhalten einerseits ein Kartenset „Schritte der schriftlichen Division“, sowie anderseits Aufgabensammlungen, die sich inhaltlich auf die Basisaufgabe, mögliche Basisaktivitäten, die Reduktion und auch die Erweiterung beziehen.

Basisaufgabe
„Dividiere große Zahlen. Achte auf die Stellenwerte.“
Material: Aufgabenkarten aus dem Materialpaket (ohne Null und ohne Rest (vierstellig)), Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier
In der Aufgabenstellung kompakt wird eine verstehensorientierte, materialgestützte Anwendung des schriftlichen Algorithmus der Division gefördert. Dazu erhalten die Kinder ein Kartenset, das den Divisionsalgorithmus schrittweise darstellt (Kartenset „Schritte der schriftlichen Division“, s. Material). In dieser wird die stellengerechte, schriftliche Notation mit Materialhandlungen an der Stellentafel und einer sprachlichen Begleitung vernetzt. Für die sachgerechte Nutzung der Stellentafel ist es wichtig, dass die Lernenden eine Verknüpfung zwischen der Darstellung von Plättchen in der Stellentafel und den entsprechenden Stellenwerten herstellen können, d. h. ein Plättchen in der Hunderterspalte steht für einen Hunderter, ein Plättchen in der Einerspalte für einen Einer (s. Reduktion: „Legen von Zahlen in die Stellentafel.“).
Das Kartenset „Schritte der schriftlichen Division“ soll ausdrücklich nicht die Einführung des schriftlichen Algorithmus ersetzen. Ziel ist es vielmehr, Lernenden einen weiteren verstehensorientierten Zugang zu ermöglichen.
In der nachfolgenden Übersicht ist das Kartenset „Schritte der schriftlichen Division“ abgebildet.

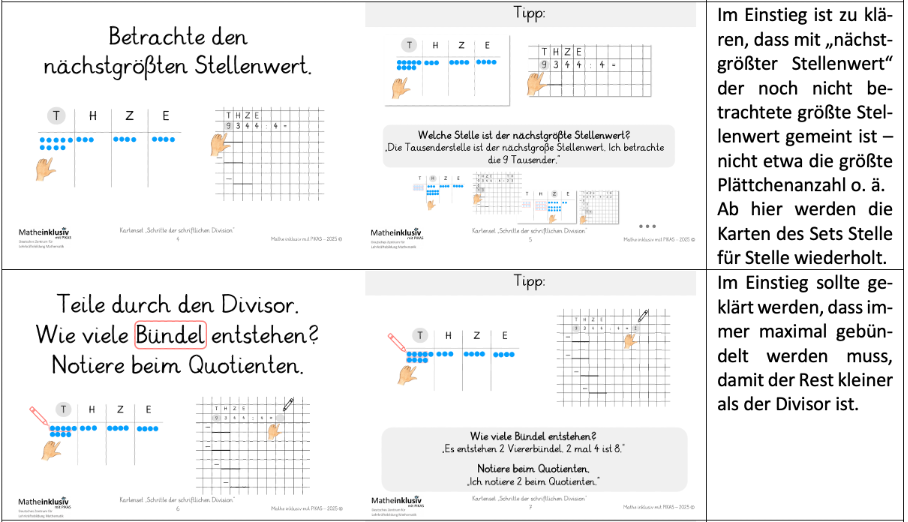
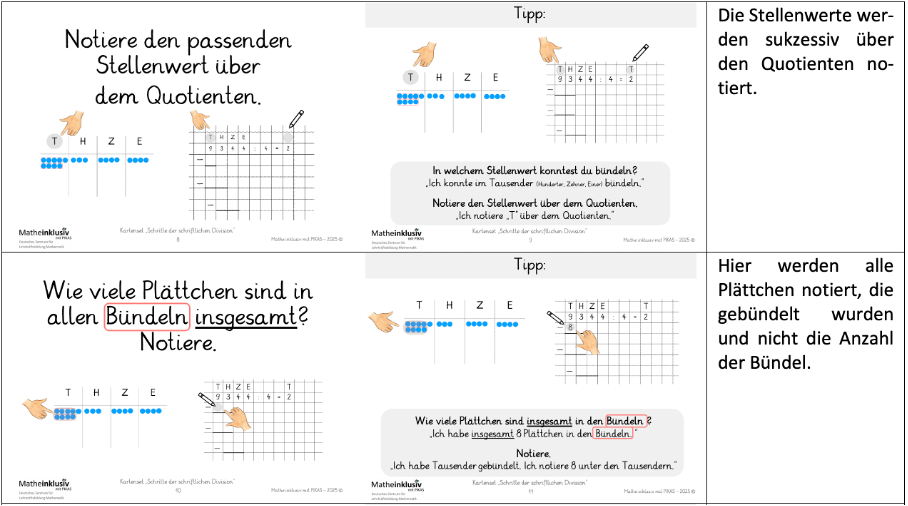
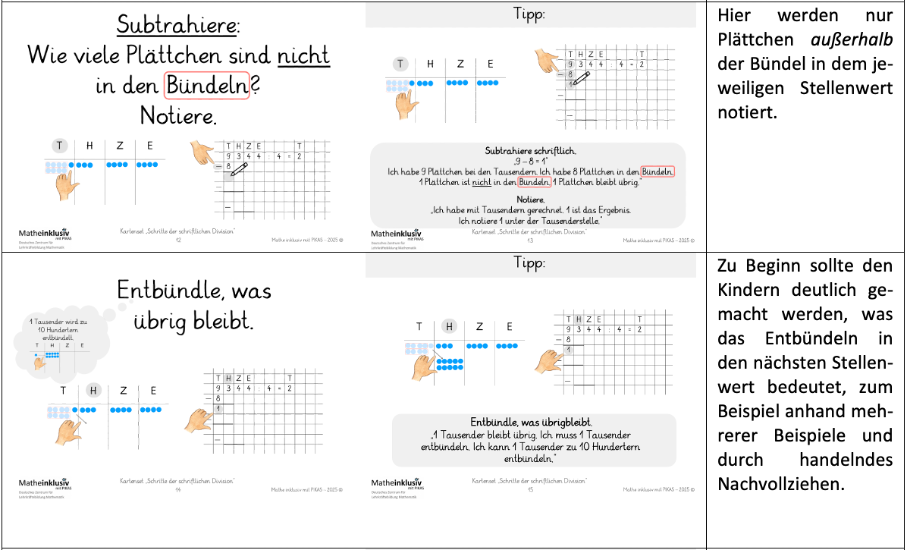

Kartenset zu „Schritte der schriftlichen Division“ und ergänzende Hinweise
Die Lernenden erhalten neben dem Kartenset „Schritte der schriftlichen Division“ Aufgabenkarten, auf denen Divisionsaufgaben mit großen Zahlen abgebildet sind. Unter Divisionsaufgaben mit „großen Zahlen“ werden hierbei die Aufgaben verstanden, die sich nicht mit wenigen Schritten halbschriftlich bzw. im Kopf lösen lassen. Bei der Erstellung der Aufgabenkarten wurde darauf geachtet, dass das Legen in die Stellentafel sowie das Bündeln und Entbündeln mit möglichst wenigen Plättchenbewegungen erfolgt. Das in dem Kartenset „Schritte der schriftlichen Division“ dargestellte Beispiel kann auf verschiedene Aufgaben adaptiert werden.
Die Lernenden legen den Dividenden mit Plättchen in die Stellentafel. Anschließend wird der in der Stellentafel gelegte Dividend durch den Divisor geteilt. Dazu werden sukzessive zunächst die Tausender, dann die Hunderter, Zehner und Einer des Dividenden durch den Divisor geteilt. Dieses Vorgehen aktiviert das Aufteilen als Grundvorstellung der Division (20 : 4 – „Wie viele Vierer kann ich bündeln?“). Nicht gebündelte Plättchen werden in den nächstkleineren Stellenwert entbündelt. Bleiben zum Beispiel zwei Plättchen bei den Tausendern übrig, werden diese in zwanzig Hunderter entbündelt. Die Lernenden wiederholen so die Schritte im Kartenset für alle Stellen, bis die Aufgabe gelöst ist.
Hinweis: Das Kartenset bildet für eine Beispielaufgabe die Aufteilung des Tausenders vollständig ab. Danach müssen die Lernenden die Vorgehensweise für den nächsten Stellenwert adaptieren.
Oben wurde beschrieben, wie das Kartenset „Schritte der schriftlichen Division“ genutzt werden kann, um den Algorithmus Schritt für Schritt zu erfassen. Alle Karten können jedoch auch einzeln genutzt werden, wenn der Fokus auf eine bestimmte Stelle des Algorithmus gelegt werden soll. Dies gilt insbesondere für die Reduktion. Hier können Lernende zu Expert*innen für einzelne Schritte des schriftlichen Algorithmus werden – beispielsweise das Entbündeln in den nächstkleineren Stellenwert, das Aufteilen durch Erstellen von Bündeln o. ä.
In Praxiserprobungen hat sich gezeigt, dass die Lernenden das Kartenset intensiv nutzen, um miteinander ins Gespräch zu kommen, Vorgehensweisen auszuhandeln und zu Schritte begründen. Die erste Erprobung des Kartensets kann somit zeitintensiv sein. Das „Zeit nehmen“ kann den Kindern jedoch helfen, einen verstehensorientierten Zugang zu erlangen und den Algorithmus mit Materialhandlungen verbinden zu können.
Mögliche Basisaktivität
„Erklären des Algorithmus der schriftlichen Division mit der Stellentafel.“
Material: Aufgabenkarten aus dem Materialpaket [ohne Null und ohne Rest (vierstellige Zahlen)], Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier, ggf. Tablet
In dieser möglichen Basisaktivität erklären die Kinder aktiv den schriftlichen Algorithmus mit eigenen Worten anhand von Material in der Stellentafel. Die Kinder adressieren dabei andere Kinder, die den Algorithmus noch nicht kennen. Dazu können folgende Aktivitäten anregen:
- Eine Aktivität könnte das Erklären des Kartensets „Schritte der schriftlichen Division“ sein. Dazu können die Kinder ein Lernvideo aufnehmen und den schriftlichen Divisionsalgorithmus fiktiven Kindern materialgestützt erklären.
- Eine weitere Möglichkeit ist, dass die Lernenden das Kartenset ohne Tippkarten erhalten und die Tippkarten selbst erstellen. Sie werden dazu aufgefordert, Plättchen und die Stellentafel zu verwenden und die Schritte auf Karten zu erklären.
Mögliche Impulsfragen:
- „Stelle dir vor, du möchtest jemandem die schriftliche Division erklären. Du kannst das Kartenset nutzen, die Stellentafel, Plättchen und kariertes Papier. Nutze den Sprachspeicher als Unterstützung und erkläre.“
- „An welchen Stellen fällt es dir schwer, eine Erklärung zu finden? Warum?“
- „Überlege genau mit einem Partner: Was machst du in dem 1. (2., 3., etc.) Schritt?“
- „Lege jeden Schritt mit Plättchen an der Stellentafel. Wie wird hier gebündelt? Gibt es Plättchen, die nicht in Bündeln sind? Muss entbündelt werden?“
- „Wo siehst du diese Ziffer aus dem schriftlichen Algorithmus in der Stellentafel?“
- „Wo findest du diese Bündel in dem schriftlichen Algorithmus wieder?“
- „Höre dir deine Aufnahme mit einem Partner an: Was kannst du gut verstehen, was kannst du verbessern?“
- …
Mögliche Basisaktivität
„Erforschen des Rests“
Material: Aufgabenkarten aus dem Materialpaket [ohne Null und mit Rest (dreistellig und vierstellig)], Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier

Die letzte Karte des Kartensets führt die Lernenden an den Punkt, an dem in der Einerspalte Plättchen verbleiben, die sich nicht mehr zu einem vollständigen Bündel zusammenfassen lassen. In dem Aufgabenbeispiel der Abbildung bleibt der Rest zwei übrig (s. Abbildung 5).
Daran anschließend kann mithilfe von Impulsfragen über den Zusammenhang zwischen schriftlicher und bildlicher Darstellung des Rests gesprochen werden (s. u.).
Impulsfragen könnten sein:
- „Betrachte den Quotienten in der Stellentafel und im schriftlichen Algorithmus. Was fällt dir auf?“
- „Warum ist das so?“
- „Bei welchen Aufgaben ist das noch so?“
- …
Sind die Lernenden noch nicht mit Dezimalzahlen vertraut, stoppen sie beim Lösen der Divisionsaufgaben beim letzten Stellenwert und notieren ggf. einen Rest.
Durch das materialgestützte Lösen von Divisionsaufgaben mit Plättchen in der Stelltafel können die Lernenden die konkrete Menge eines Rests erfassen und aufgabenbezogen interpretieren.
Ein exemplarisches Lernendengespräch ist in Abbildung 6 aufgeführt:
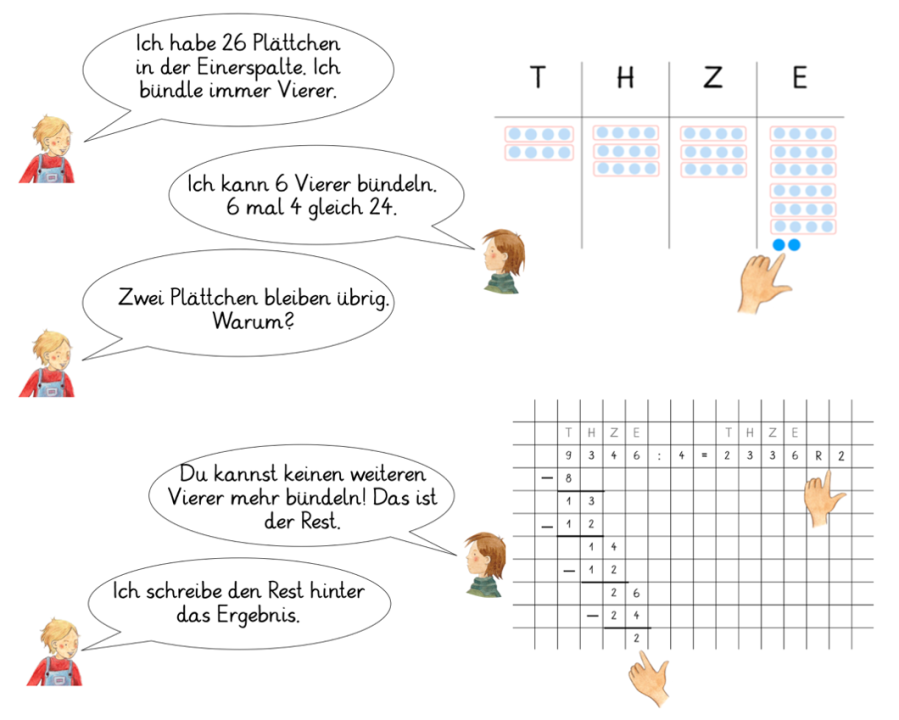
An dieser Stelle sei auf die Bedeutung einer präzisen Sprache hingewiesen: Bestimmte Formulierungen wie „Vier passen nicht in zwei“ oder „Vier in zwei, das geht nicht“ sollten vermieden werden, da sie fachlich ungenau sind und den Anschluss an weiterführende mathematische Konzepte verhindern. Im weiteren Verlauf des Mathematiklernens zeigt sich, dass vier 0,5-mal in zwei passen. Für das Verständnis und den schriftlichen Algorithmus der Division ist daher eine exakte Ausdrucksweise erforderlich.
Mögliche Basisaktivität
„Sprechen über die Null im Algorithmus“
Material: Aufgabenkarten aus dem Materialpaket [mit Null und ohne Rest (dreistellig und vierstellig)], Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier
Beim stellenweisen Aufteilen im schriftlichen Algorithmus sind Nullen eine typische Schwierigkeit (s. Hintergrund). In dieser Basisaktivität können unterschiedliche Positionen der Null und der Umgang mit diesen erkundet werden. In den Abbildungen 7 und 8 sind verschiedene Beispiele der Position der Null im schriftlichen Algorithmus abgebildet.

Im Zusammenhang mit der schriftlichen Division tritt die Null an verschiedenen Positionen auf, was für die Lernenden eine besondere Herausforderung darstellen kann. Besonders schwierig ist der Aufbau tragfähiger Vorstellungen zur Null für Kinder, die diese vor allem mit ‚Nichts‘ verbinden. Sie neigen dazu, diese Teilschritte auszulassen (Padberg & Benz, 2021, S. 314). Eine Null kann als Teilergebnis der Subtraktion entstehen (s. Hand Nr. 1 in Abbildung 7). Sie wird außerdem notiert, wenn eine Ziffer des Dividenden Null ist oder in einem Stellenwert keine Plättchen vorhanden sind (s. Hand Nr. 2 in Abbildung 7). Es wird ebenfalls eine Null notiert, wenn die Zahl zu klein ist, um Bündel in der Größe des Divisors zu bilden (s. Hand Nr. 3 in Abbildung 7). Schließlich muss auch die Null im Quotienten korrekt notiert werden: Kann in einem Stellenwert kein Bündel hergestellt werden, weil zu wenige Plättchen vorliegen, so wird an der entsprechenden Stelle im Quotienten eine Null eingetragen (s. Hand Nr. 4 in Abbildung 7 und Abbildung 8).
Grundsätzlich wird die Null wie jede andere Ziffer notiert. Die verkürzte Schreibweise ist die einzige Möglichkeit, dass die Null als erste Ziffer des Ergebnisses weggelassen werden kann, d. h. anstelle von 0611 kann die Zahl 611 notiert werden (s. Abbildung 8). Dies ist möglich, da innerhalb des ersten Stellenwertes keine Bündel in der Größe des Divisors gebildet werden können – im unten dargestellten Beispiel ist das der Tausender (s. Abbildung 8). Die Tausender werden unmittelbar in Hunderter entbündelt. Die Tausenderstelle enthält damit 0 Einheiten. Da das Entbündeln werterhaltend ist (z. B. 1 T = 10 H), ändert das Weglassen der Anfangsnull den Zahlenwert nicht. Weil die weitere Rechnung auf der Hunderterebene fortgesetzt wird, kann auch die Ergebnisnotierung an der Hunderterstelle beginnen (s. Hintergrund).

Die Lernenden erhalten in dieser möglichen weiterführenden Basisaktivität Aufgabenkarten, die explizit das Thema Nullen an verschiedenen Stellen innerhalb des Algorithmus fokussieren.
Die Aufgaben fordern und fördern einen verstehensorientierten Umgang mit Nullen beim Aufteilen und bei der Notation von Teilergebnissen. Zudem können die Lernenden mithilfe von Impulsfragen den Umgang mit der Null an verschiedenen Stellen erkunden und reflektieren.
Darüber hinaus können bereits gelöste Aufgabenkarten verglichen und reflektiert werden. Dazu gibt es Aufgaben mit verschiedenen Lösungen, von denen jeweils eine korrekt ist. Beispielsweise können als Lösungen für die Aufgabe 6321 : 7 diese drei Möglichkeiten angegeben werden: 0903, 903 oder 93. Durch den materialgestützten Umgang mit dem Kartenset „Schritte der schriftlichen Division“ können potenzielle Fehlerquellen erkannt und nachvollzogen werden.
Mögliche anschließende Impulsfragen zur Auseinandersetzung mit der Null:
- „Wann kann ich die ersten beiden Stellen zusammenfassen?“
- „Warum muss hier die Null notiert werden?“
- „Wo kann die Null weggelassen werden?“
- „Was passiert, wenn nach dem Entbündeln zu wenige oder keine Plättchen in einem Stellenwert liegen?“
- …
Mögliche Basisaktivität
„Vergleichen von verwandten Aufgaben“
Material: Aufgabenkarten aus dem Materialpaket (Aufgabenserien), Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier
Um Zusammenhänge zwischen Aufgaben sowie weiterführende Erkenntnisse über die einzelnen Schritte des Algorithmus zu erkunden, kann der Fokus auf Divisionsaufgaben, die in einem inhaltlichen Zusammenhang miteinander stehen, gerichtet werden. Durch Vergleiche der Lösungen sowie der Ergebnisse, können gezielt Aufgabenbeziehungen in den Blick genommen werden.
In dieser Basisaktivität stehen verschiedene Aufgabenserien zur Auswahl, z. B. Aufgaben zu:
- Verdopplungen des Dividenden (z. B. 312 : 3 und 624 : 3 und 1248 : 3) bzw. des Divisors (1248 : 3 und 1248 : 6 und 1248 : 12)
- Stufenzahlen (z. B. 312 : 3 und 3120 : 3 und 31200 : 3)
- dem Dividieren durch unterschiedliche Divisoren (z. B. durch 2, 4 und 8; 5 und 10; 4, 6 und 8 etc.)
- Konstanz des Quotienten (z. B. 312 : 3 und 624 : 6 oder 1248 : 3 und 4992 : 12).
Die Kinder vergleichen die Rechenwege der Aufgaben und erkunden Gemeinsamkeiten und Unterschiede. Dabei können durch Impulsfragen verschiedene Reflexionswege angestoßen werden.
Mögliche Impulsfragen:
- „Was fällt dir auf? Was verändert sich? Was bleibt gleich?“
- „Wie viele Plättchen müssen entbündelt werden?“ (pro Schritt)
- „Wie viele Plättchen sind nicht in Bündeln?“ (pro Schritt)
- „Wie viele Bündel entstehen?“ (pro Schritt)
- „Wo entstehen Nullen und wo werden sie notiert?“
- „Warum entstehen Nullen bei deinem Rechenweg? Beschreibe und zeige an der Stellentafel.“
- „Warum musst du sie notieren? Wie verändert sich dein Ergebnis, wenn du sie weglässt?“
- ...
Mögliche Basisaktivität
„Beschreiben und vergleichen von Rechenwegen“
Material: Aufgabenkarten aus dem Materialpaket (beliebig), ggf. Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier
In dieser Basisaktivität vergleichen die Kinder Rechenwege, um Zusammenhänge, Unterschiede und Strukturen von Aufgaben zu erkunden. Das Ziel des Vergleichens ist die Sensibilisierung für einzelne Stellen im Algorithmus sowie Zusammenhänge zu anderen Rechenwegen herzustellen. Die Lernenden erhalten Aufgabenkarten aus dem Materialpaket. Die Lernenden lösen zunächst eine Aufgabe mit einem Rechenweg ihrer Wahl, z. B. schriftlich, materialgestützt mithilfe des Kartensets, halbschriftlich oder im Kopf. Sie vergleichen ihren eigenen Lösungsweg mit den Lösungswegen der anderen Lernenden. Die Lernenden können so auf einer Metaebene die Lösungsprozesse reflektieren und diese erkunden.
Dabei können verschiedene Themenschwerpunkte gelegt werden. Beispielsweise kann der Zusammenhang zwischen der halbschriftlichen Strategie des schrittweisen Dividierens und dem schriftlichen Divisionsalgorithmus erkundet werden. Eine weitere Vergleichsmöglichkeit sind Aufgaben mit unterschiedlichen Divisoren (z. B. 2 und 4, oder 3 und 6, oder 5 und 10). Auch hier können Impulsfragen mögliche Denkwege anstoßen:
- „Was fällt dir auf? Was verändert sich? Was bleibt gleich?“
- „Wie viele Plättchen müssen entbündelt werden?“ (pro Schritt)
- „Wie viele Plättchen sind nicht in Bündeln?“ (pro Schritt)
- „Wie viele Bündel entstehen?“ (pro Schritt)
- „Wo entstehen Nullen und wo werden sie notiert?“
- …
Reduktion
„Ergänzungskarten nutzen“
Material: Aufgabenkarten aus dem Materialpaket [ohne Null und ohne Rest (vierstellig)], Kartenset „Schritte der schriftlichen Division“, Ergänzungskarten zum Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier
Im Kartenset „Schritte der schriftlichen Division“ wird das Aufteilen des 1. Stellenwertes exemplarisch abgebildet. Danach beginnen die Lernenden das Kartenset von vorne und übertragen das Aufteilen auf die weiteren Stellenwerte. Sie können sich sukzessive von den Karten des Sets als Unterstützung lösen.
In dieser Reduktion nutzen die Lernenden zusätzlich zu dem Kartenset „Schritte der schriftlichen Division“ Ergänzungskarten, in denen alle Schritte bis zur vollständigen Lösung der Divisionsaufgabe begleitet werden. Die Ergänzungskarten können flexibel zum Basiskartenset ergänzt werden. Dadurch entsteht ein vollständiges Set, welches die Lernenden durch die gesamte Aufgabe begleitet.
Reduktion
„Legen von Zahlen in die Stellentafel“
Material: Forschungsblätter aus dem Materialpaket zu „Zahlen in die Stellentafel legen“, Stellentafel, Plättchen
Zur Förderung des Stellenwertverständnisses (s. Inhalte: Stellenwertvorstellungen: Hintergrund) wird in dieser Reduktionsaufgabe das Legen von Zahlen in die Stellentafel verstehensorientiert wiederholt. Mögliche Aktivitäten können folgende sein:
- Mit einer konstanten Anzahl an Plättchen verschiedene Zahlen in die Stellentafel legen.
- Zahlen legen, die durch eine vorgegebene Zahl (z. B. 2 oder 4) ohne Rest teilbar sind.
- …
Die Kinder dokumentieren, welche Zahlen sich legen lassen und begründen, warum sie alle Möglichkeiten gefunden haben.

Abbildung 10: Forschungsblätter aus dem Materialpaket zu „Zahlen in die Stellentafel legen“
Weitere Aktivitäten zum Aufbau eines Stellenwertverständnisses befinden sich auf
- Mathe sicher können: Förderbaustein N1 Stellenwerte verstehen
- Mathekartei. Einstiege - Rituale - Spiele - Übungen (Karte 22, 23, 37)
-
FÖDIMA - Kartei. Diagnose - und Förderanregungen Arithmetik Klasse 1 und 2 (Karte 12, 15)
Reduktion
„Fokussieren der Grundvorstellung Aufteilen“
Material: Forschungsblätter aus dem Materialpaket zu „Fokussierung des Aufteilens“, Plättchen
Der schriftliche Divisionsalgorithmus basiert auf der Grundvorstellung des Aufteilens (s. Hintergrund). Die folgende Reduktion hat zum Ziel, materialgestützt und verstehensorientiert das Aufteilen - eine Grundvorstellung der Division - zu festigen.
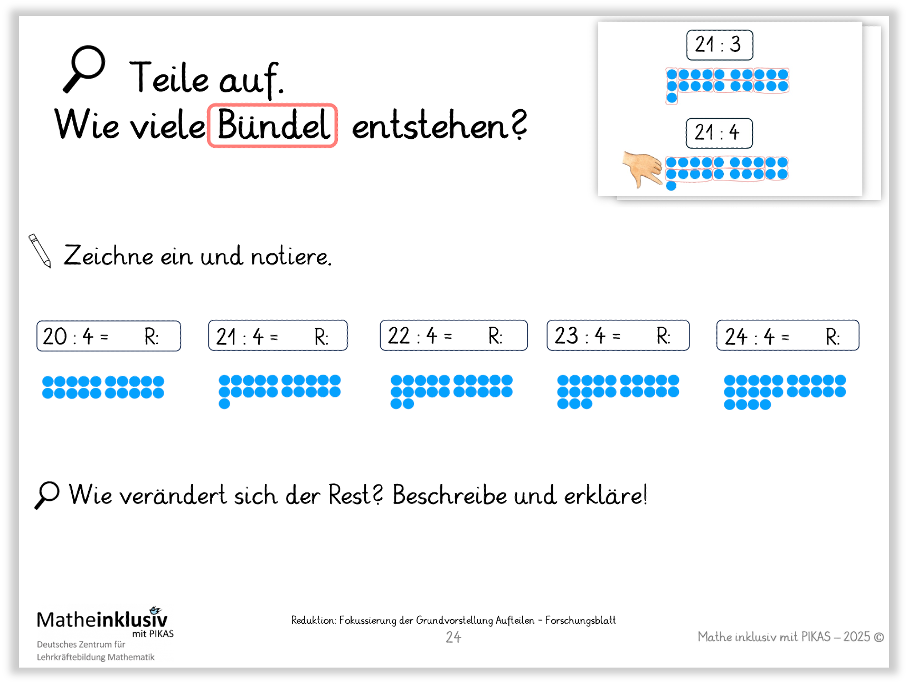
Die Kinder erhalten ein Forschungsblatt zu Fokussierung des Aufteilens sowie Plättchen. Sie sollen die Gesamtmenge mit dem vorgegebenen Divisor aufteilen, indem sie die Bündel (ggf. nachlegen) einzeichnen und die Anzahl der Bündel notieren.
Einige Aufgaben sind so gewählt, dass ein Rest entsteht (s. „Mögliche Basisaktivität: Dividieren mit Rest“). Nach dem Einzeichnen der Bündel analysieren die Kinder die Aufgabenserien und reflektieren, wie sich der Rest verändert. Dabei können sie erkennen, dass manche Zahlen ohne Rest aufgeteilt werden können, andere nicht und der Rest stets kleiner ist als ein vollständiges Bündel.
Weitere Aktivitäten rund um das Aufteilen (ohne Rest) befinden sich auf Mathe sicher können: Digitale Pinnwand zum Material N4B „Division verstehen“.
Reduktion
„Fokussieren des Bündelns und Entbündelns“
Material: Forschungsblätter aus dem Materialpaket zu „Fokussierung des Bündelns und Entbündelns“, Stellentafel, Plättchen
Die Entbündelung von Stellenwerten ist ein wesentlicher Bestandteil des schriftlichen Divisionsverfahrens.Entsteht beim Dividieren ein Rest, muss dieser im nächsten Rechenschritt entbündelt werden (s. Hintergrund). Die folgende Reduktion thematisiert das Bündeln und Entbündeln mithilfe der Stellentafel im reduzierten Zahlenraum. Ziel ist es, das Verständnis der Kinder dafür zu fördern, wie Stellenwerte in die jeweils nächstgrößere bzw. kleinere Einheit gebündelt bzw. entbündelt werden können. In Abbildung 12 ist ein Auszug aus dem Materialpaket dargestellt.

Abbildung 12: Forschungsblätter aus dem Materialpaket zu „Fokussieren des Bündelns und Entbündelns“
In dieser Aufgabe erkunden die Kinder, wie viele Hunderter, Zehner oder Einer eine vorgegebene Zahl enthält. Dafür erhalten sie Forschungsblätter mit dem Fokus auf (Ent-)Bündelungen in der Stellentafel, eine Stellentafel sowie Plättchen. Sie legen die auf der Karte vorgegebene Anzahl mit Material stellengerecht in die Stellentafel, führen anschließend die entsprechende (Ent-)Bündelung durch, notieren die Zahl und beschreiben sowie begründen ihre Beobachtungen (s. Abbildung 12).
So wird der Zusammenhang zwischen Stellenwerten handelnd nachvollzogen und die Grundlage für anschließende Entbündelungsprozesse im Rechenverfahren gelegt.
Weitere Aktivitäten zur Förderung des Verständnisses für das Entbündeln und Bündeln von Zahlen befinden sich unter:
- Mathe sicher können: N1 B ‘Ich kann bündeln und entbündeln‘.
- Mathekartei. Einstiege - Rituale - Spiele - Übungen (Karte 22 und 23)
- FÖDIMA - Kartei. Diagnose - und Förderanregungen Arithmetik Klasse 1 und 2 (Karte 12)
Reduktion
„Verringern des Zahlenraums“
Material: Aufgabenkarten aus dem Materialpaket (ohne Null/ohne Rest (dreistellig), Kartenset „Schritte der schriftlichen Division – Verringerter Zahlenraum“, Plättchen, Stellentafel, kariertes Papier

Abbildung 13: Kartenset „Schritte bei der schriftlichen Division – Verringerter Zahlenraum“
In dieser Reduktion bearbeiten die Lernenden die Basisaufgabe in einem reduzierten Zahlenraum. Dabei erhalten sie ein Kartenset, welches den Algorithmus für dreistellige Zahlen verständnisbasiert begleitet – vergleichbar zu dem Kartenset „Schritte der schriftlichen Division“. Dies verringert die Anzahl der Schritte und entlastet das Arbeitsgedächtnis. Die zugehörigen Aufgaben aus dem Materialpaket sind zusätzlich so ausgewählt, dass innerhalb des Algorithmus nur ein kleiner Rest bzw. gar kein Rest bleibt. Die Lernenden müssen kleinere Mengen entbündeln und im nächsten Stellenwert demzufolge auch nur mit kleineren Zahlen rechnen. Wichtig ist es hierbei zu berücksichtigen, dass die Aufgaben sich nicht in wenigen Schritten halbschriftlich, bzw. im Kopf lösen lassen (z.B. 400 : 4). Es ist immer vorzuziehen, dass die Lernenden solche Aufgaben nicht schriftlich lösen, sondern bekannte Strategien nutzen.
Erweiterung
„Untersuchen von Divisions-Aufgabenserien mit Rest“
Material: Aufgabenkarten aus dem Materialpaket (Aufgabenserien mit Rest), Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier
In dieser Erweiterung können die Lernenden die Zusammenhänge unterschiedlicher Aufgaben mit Rest erkunden. Dazu können sowohl die Aufgaben und deren Lösungswege als auch der Rest in den Fokus genommen werden. Im Folgenden werden mehrere Möglichkeiten skizziert:
- Die Lernenden erhalten Kärtchen mit Aufgabenserien, bei welchen ein jeweils unterschiedlicher Rest übrigbleibt (z. B. 8404 : 4 und 8403 : 4 und 8405 : 4). Diese Aufgaben können zunächst mithilfe des Kartensets gelöst werden. Daraufhin kann ein Vergleich gezogen werden. Hier können nun Erkundungsprozesse frei oder durch Impulsfragen oder Beobachtungsaufträge initiiert werden.
-
Die Lernenden erhalten lediglich eine Aufgabe (z. B. 8404 : 4) und können daran angelehnt weitere Aufgaben mit einem vorgegebenen Rest erfinden. Dabei steht ihnen frei, ob der Divisor oder der Dividend (egal an welcher Stelle) verändert werden soll.
- Eine weitere Möglichkeit wäre ein freier Auftrag, (vierstellige) Aufgaben mit einem vorgegebenen Rest zu erfinden, ohne dass eine Aufgabenkarte vorgegeben wird. Über das eigene Erfinden oder Verändern von Aufgaben, können die Lernenden an das Verstehen anknüpfende Einsichten in die Schritte des Algorithmus erlangen.
- Hier erhalten die Lernenden Aufgaben, bei denen im Dividenden jeweils eine bzw. zwei Ziffer(n) entfallen sind (z. B. 12_4 : 4 oder _2_4 : 4). Die Lernenden könnten den Auftrag erhalten, die Lücken so zu füllen, dass ein vorgegebener Rest entsteht (z. B. Rest 0, Rest 2, Rest 4, Rest 6, etc.).
Um Vergleiche zwischen den Aufgaben zu ziehen oder metakognitive Prozesse im Erkunden von Zusammenhängen anzustoßen, können Impulsfragen unterstützen:
- „Was haben die Dividenden gemeinsam? Wo sind Unterschiede? Wie hängen sie zusammen?“
- „Was fällt dir auf? Was verändert sich? Was bleibt gleich?“
- „Wie viele Plättchen bleiben hier als Rest übrig? Und wie viele hier?“
- „Wie viele Plättchen müssen entbündelt werden? (pro Schritt)
- „Wie viele Plättchen sind nicht in Bündeln?“ (pro Schritt)
- „Wie viele Bündel entstehen?“ (pro Schritt)
- „Wie hängen die Divisoren zusammen?“
- …
Erweiterung
„Erkunden der Dezimalschreibweise mit der erweiterten Stellentafel“
Material: Aufgabenkarten aus dem Materialpaket (Aufgaben ohne Null mit Rest (dreistellig und vierstellig), Aufgabenserien mit Rest), Tippkarte (s.u.), Kartenset „Schritte der schriftlichen Division“,Plättchen, erweiterte Stellentafel, kariertes Papier
In dieser Erweiterung erkunden die Lernenden Divisionsaufgaben, deren Ergebnis eine Dezimalzahl ist und nutzen dafür die erweiterte Stellentafel. Voraussetzend dazu sollten Kinder Aufgaben mit Rest erkundet haben.
Der zuvor bloß notierte Rest wird dann analog zu den vorherigen Schritten in Zehntel, Hundertstel etc. weiter entbündelt und im Ergebnis mit einem Komma notiert. So können Aufgaben mit Rest in einer Dezimalzahlschreibweise genauer dargestellt werden. Die einzelnen Schritte können ebenfalls analog zu den vorherigen Schritten in der erweiterten Stellentafel dargestellt werden.
Die Lernenden können zur Einführung eine Tippkarte erhalten, die ergänzend zum Kartenset ausgeteilt wird und zur Erkundung der erweiterten Stellentafel anregt (s. Abbildung 14).

Abbildung 14: Tippkarte aus dem Materialpaket zu: „Erkunden der Dezimalschreibweise mit der erweiterten Stellentafel“
In der erweiterten Stellentafel kann der verbleibende Rest schrittweise weiter aufgeteilt werden. Dazu wird die Stellentafel rechts neben der Einerstelle um Zehntel bzw. Hundertstel und Tausendstel erweitert (s. Abbildung 15). Das Kartenset kann weiterhin Anwendung finden, indem auch in diesen Stellenwerten gebündelt und entstehende Reste entbündelt werden.

Abbildung 15: Vorgehen bei Dezimalergebnissen an der erweiterten Stellentafel
Die Lernenden werden dazu angeregt, über die Bedeutung der Stellenwerte nach dem Komma zu reflektieren und deren Zusammenhang mit der Division zu erkennen. Weiterhin können sie die Bedeutung des Kommas erkunden. Impulsfragen können sein:
- „Kannst du den Rest weiter aufteilen? Begründe.“
- „Welche Stellenwerte sind „neu“?“
- „Wann schreibe ich ein Komma?“
- „Was bedeutet die dicke Linie in der erweiterten Stellentafel zwischen den Einern und den Zehnteln?“
- „Was bedeutet ein Plättchen bei den Zehnteln? Wie unterscheidet es sich von einem Plättchen bei den Einern?“
- „Wie verändert sich die Zahl, wenn du eine Stelle weiter nach rechts gehst?“
- „Wie viele Hundertstel sind ein Zehntel?“
- „Wie kannst du eine Zahl mit Komma in der Stellentafel darstellen?“
- „Wie erkennst du, dass eine Division vollständig durchgeführt wurde – auch mit Rest?“
- …
Erweiterung
„Dividieren durch mehrstellige Zahlen und Ergebnisse vergleichen“
Material: Aufgabenkarten aus dem Materialpaket (Aufgaben mit mehrstelligem Divisor), Kartenset „Schritte der schriftlichen Division“, Plättchen, Stellentafel, kariertes Papier, Stellentafel (bis Millionen)
In dieser Erweiterungsaufgaben erkunden die Lernenden, wie die einzelnen Schritte des schriftlichen Algorithmus auf mehrstellige Divisoren angewandt werden können (z. B. 136 596 : 12; 67 525 : 365; etc.) und wie sich die Stellenwertbezeichnungen im Ergebnis im Vergleich zum Dividieren mit einstelligen Divisoren unterscheiden. Ähnlich, wie in der Basisaktivität „Umgang mit Nullen in Divisionsaufgaben“ ist es hier möglich direkt die ersten zwei bzw. drei oder vier Stellen in den Blick zu nehmen. Dadurch entfallen die Nullen im Ergebnis, die entstehen, wenn Stelle für Stelle vorgegangen wird. Dies ist bei der Beschriftung der Stellenwerte im Ergebnis zu beachten.
Die Lernenden können entdecken, dass das Vorgehen genau wie bei einstelligen Divisoren funktioniert. Dazu können beispielsweise gelöste Aufgaben mit einstelligen Divisoren mit Aufgaben mehrstelliger Divisoren vergleichen werden.
Impulsfragen könnten sein:
- „Was fällt dir auf?“
- „Was bleibt gleich? Was ist unterschiedlich?“
- „Wie können die Stellenwerte im Ergebnis aufgeschrieben werden?“
- „Wie kann mit mehrstelligen Divisoren gerechnet werden?“
- „Wie unterscheiden sich die einzelnen Bündel?“
- „Wie würde es aussehen, wenn…? (bei Aufgaben mit großen Divisoren)“
- …
Möglichkeiten individueller Unterstützung
„Zur motorischen Unterstützung Holzplättchen und rutschfestes Material verwenden“
Material: Wendeplättchen aus Holz, Filzunterlage
Zur motorischen Unterstützung können griffige Wendeplättchen aus Holz und rutschfeste Unterlagen beispielsweise aus Filz verwendet werden (s. Abbildung 16).

Abbildung 16: Rutschfeste Filzunterlage und Wendeplättchen aus Holz
Möglichkeiten individueller Unterstützung
„Zur kognitiven Unterstützung eine „Lupe“ verwenden“
Material: Folie „Lupe“
Durch Auflegen und Verschieben einer Folie / „Lupe“ kann ein einzelner Rechenschritt oder eine Plättchenmenge in der Stellentafel fokussiert werden. Die anderen Plättchen werden ausgeblendet, sind durch die durchsichtige Folie dennoch sichtbar. Sie unterstützt das Fokussieren von Teilmengen, ohne dass der Rest der Abbildung verdeckt oder weggenommen wird. Außerdem lenkt dieses Vorgehen die Aufmerksamkeit auf die Stelle, die beachtet werden soll. Zur Erstellung der Lupe können z. B. aus farbigen Prospekthüllen Winkel erstellt werden (s. Abbildung 17).
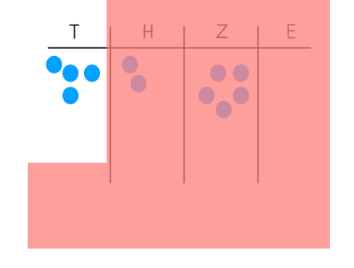
Abbildung 17: Verwendung einer „Lupe“ zur Orientierung auf der Stellentafel
Möglichkeiten individueller Unterstützung
„Zur sprachlichen Unterstützung einen Sprachspeicher anlegen und Audioaufnahmen nutzen“
Das Kartenset „Schritte der schriftlichen Division“ ist möglichst sprachbildend gestaltet, kann jedoch aufgrund der Textlastigkeit für einige Kinder sprachlich herausfordernd sein. Zur sprachlichen Entlastung kann es hilfreich sein, die Hinweise und Tipps des Kartensets zusätzlich als Audioaufnahmen bereitzustellen, z. B. mithilfe eines Audiostifts oder eines Tablets. So wird insbesondere leseunsicheren oder überwiegend auditiv lernenden Kindern der Zugang erleichtert. Weiterhin besteht die Möglichkeit, dass auch Kinder Audioaufnahmen erstellen und diese zur Verbalisierung ihrer Erklärungen nutzen.

Abbildung 18: Audioaufnahmen nutzen
Darüber hinaus bietet es sich an, die Beschreibungen der Rechenschritte zur schriftlichen Division gemeinsam im Klassenverband in einem sogenannten Sprachspeicher zu dokumentieren.
Ein Sprachspeicher zu Grundbegriffen der Division ist bereits im Kartenset abgebildet. Er kann die Grundlage für einen Sprachspeicher der Klasse sein. Dieser sollte dynamisch in Zusammenarbeit mit den Lernenden entwickelt werden. Eine beispielhafte Darstellung ist in Abbildung 19 dargestellt. Die Gestaltung sollte an die individuellen Bedürfnisse der Klasse und auch an bereits bekannte Strukturen angepasst werden. Ein solcher Sprachspeicher kann die Kinder gezielt beim Gebrauch fachsprachlicher Strukturen unterstützen und sollte kooperativ im Unterricht entwickelt werden. Es ist wichtig, dass der Sprachspeicher nicht statisch ist, sondern sich in der Auseinandersetzung mit dem Inhalt der schriftlichen Division weiterentwickelt, indem z.B. wichtige Fachbegriffe und Satzbausteine gemeinsam ergänzt werden (s. hierzu auch Förderschwerpunkt Sprache: Unterricht; Leitideen: Austausch anregen). Abbildung 19 zeigt einen Sprachspeicher, der sich durch die Auseinandersetzung mit der schriftlichen Division dynamisch weiterentwickelt.
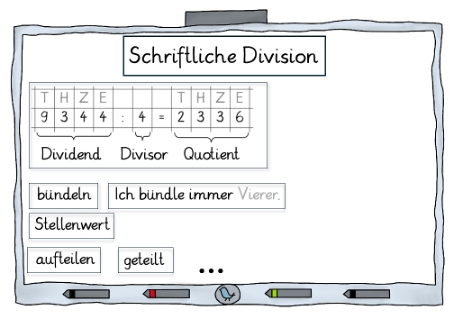
Ergänzende Wörter:
- Einer, Zehner, Hunderter, Tausender
- Bündeln, Entbündeln (gebündelt, entbündelt)
- Bündel
- Einer-/Zehner-/Hunderter-/Tausenderstelle
- Dividend, Divisor, Quotient
- Divisionskarte
- Zehntel, Hundertstel, Tausendstel
- nächstgrößter Stellenwert bzw. größter Stellenwert
- …
Ergänzende Satzbausteine:
- Ich lege 24 Plättchen in die Hunderterspalte
- Die 4 passt 6 mal in die 24.
- Ich entbündle die Hunderter.
- Jeder Zehner wird zu zehn Einern entbündelt.
- Ich gehe zur Zehnerstelle. Ich schaue mir die Zehnerstelle an.
- Es bleiben 3 Plättchen übrig. Die entbündle ich.
- …


