Aufgabenstellung kompakt
Das Verständnis der dekadischen Zahlzusammenhänge gilt ebenso wie das Verständnis der Multiplikation als Basiskompetenz am Ende der Grundschule.
Mit der Aufgabenstellung „Zehnereinmaleins“ werden die Basiskompetenzen Multiplikations- und Stellenwertverständnis am Ende der Primarstufe und zu Beginn der Sekundarstufe I miteinander verbunden aufgearbeitet (s. Hintergrund). Hierzu ist von besonderer Bedeutung, dass die Lernenden ihre Kenntnisse zum kleinen Einmaleins und zum dekadischen Aufbau der natürlichen Zahlen ebenso wie ihre Vorstellungen über Stellenwerte und zur Multiplikation strukturell sichern können. Die Aufgabenstellung kompakt geht dies an, indem sie auf die analogen Zusammenhänge zwischen dem kleinen und großen Einmaleins zielt. Materialgestützt stellen die Lernenden Aufgaben des Zehnereinmaleins und kleinen Einmaleins dar, erkunden Analogien und beschreiben diese fach- und bedeutungsbezogen sprachlich, um ein konzeptuelles Verständnis der Multiplikation von Zehnerzahlen zu entwickeln. Auf Ebene der Prozesse wird insbesondere das Vernetzen von Darstellungen (materiell, bildlich, symbolisch, sprachlich) zum Ausbau der Stellenwert- und Operationsvorstellungen im Bereich der Multiplikation vertieft (MSB NRW, 2021, S. 86 und MSB NRW, 2022, S. 27). Erwartet werden somit neben dem Darstellen auch prozessbezogene Kompetenzen im Kommunizieren, Argumentieren und Problemlösen (MSB NRW, 2021, S. 82).
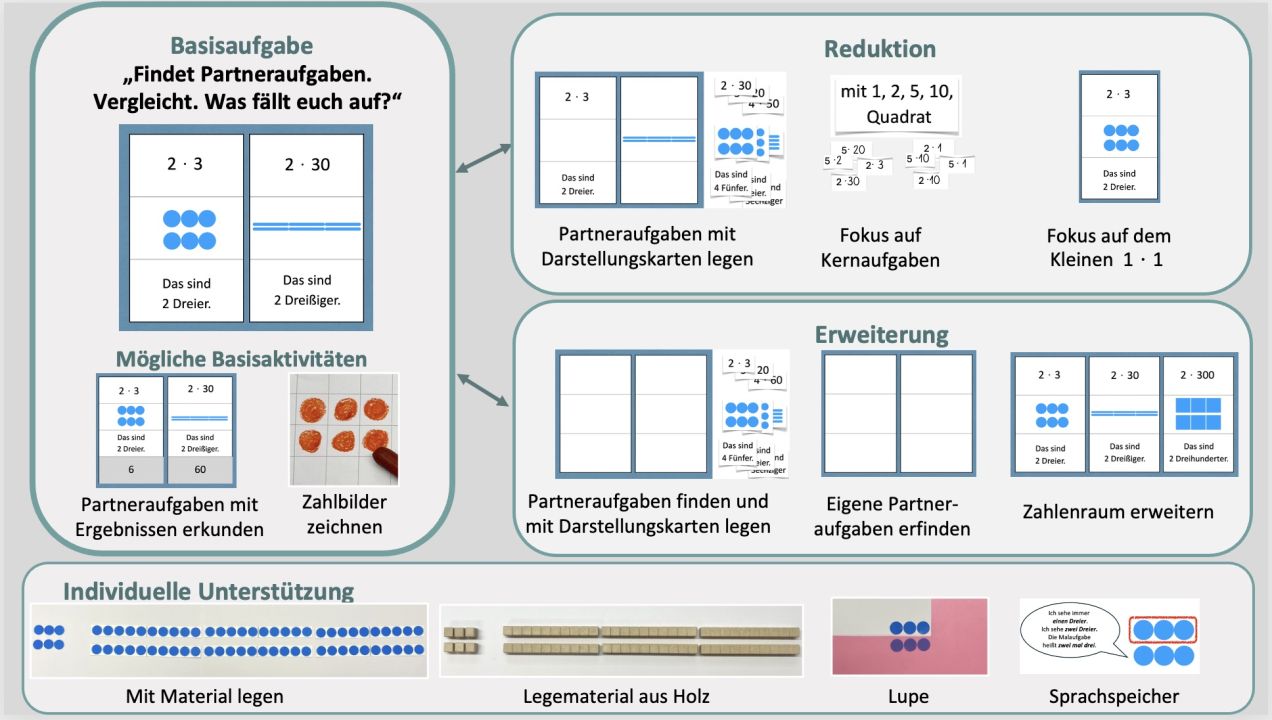
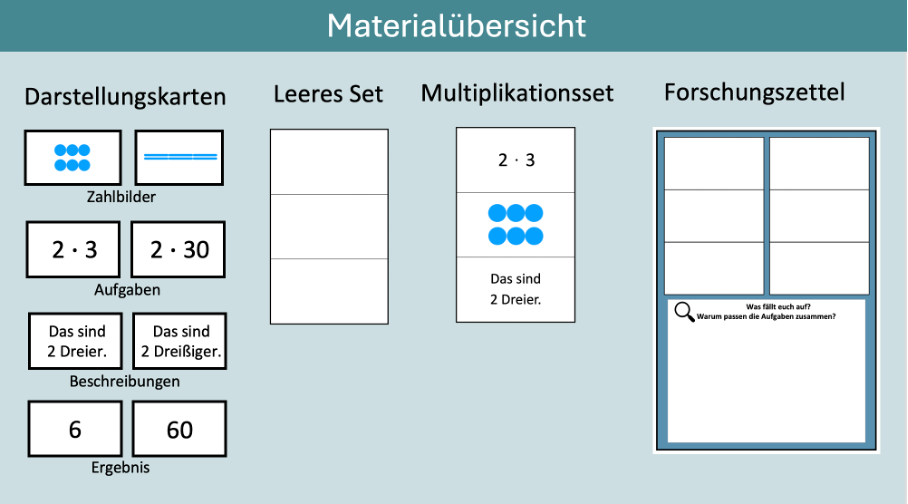
Die folgende Abbildung fasst zusammen, welche Materialien bei der Aufgabenstellung kompakt genutzt werden. Unter „Material“ finden Sie zudem zu den Basisaufgaben, den Reduktionsaufgaben, Erweiterungsaufgaben und Möglichkeiten individueller Unterstützung aufgeführt, welche weiteren Materialien Sie bei welcher Aufgabe benötigen.
Basisaufgabe
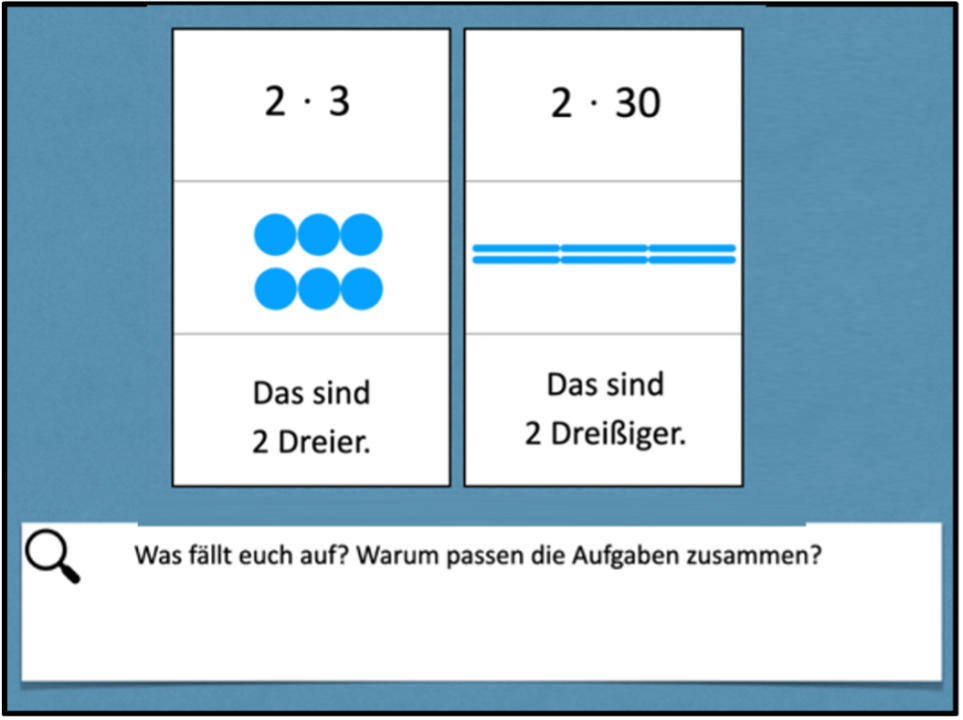
„Findet Partneraufgaben. Vergleicht. Was fällt euch auf?“
Material: leere Sets, Darstellungskarten, Forschungszettel, Klebestift
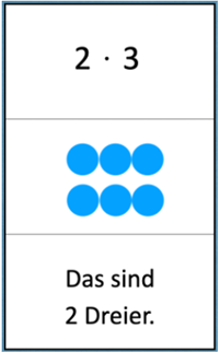
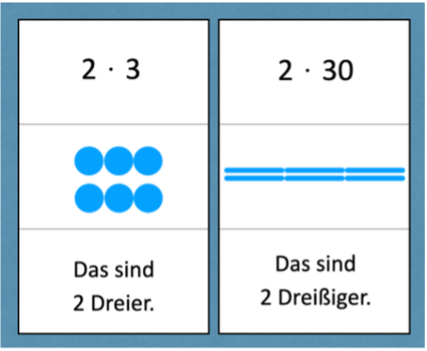
Auffälligkeiten, die die Kinder beschreiben und begründen, könnten beispielsweise sein:
- „Links habe ich zwei mal drei Einer, also zwei Dreier. Rechts habe ich zwei mal drei Zehner, also zwei Dreißiger. Das Bild sieht irgendwie ähnlich aus.“
- „Es sind genauso viele Einer wie Zehner.“
- „Ich sehe sechs Einer und sechs Zehner.“
- „2 ⋅ 3 und 2 ⋅ 30 passen gut zusammen, da zwei Dreier zu zwei Dreißigern werden.“
- „Die Einer werden zu Zehnern.“
- …
Zur sprachlichen Unterstützung kann ein Sprachspeicher verwendet werden (s. Möglichkeiten individueller Unterstützung).
Basisaktivität
„Partneraufgaben mit Ergebnissen erkunden“
Material: Multiplikationssets - mögliche Basisaktivität
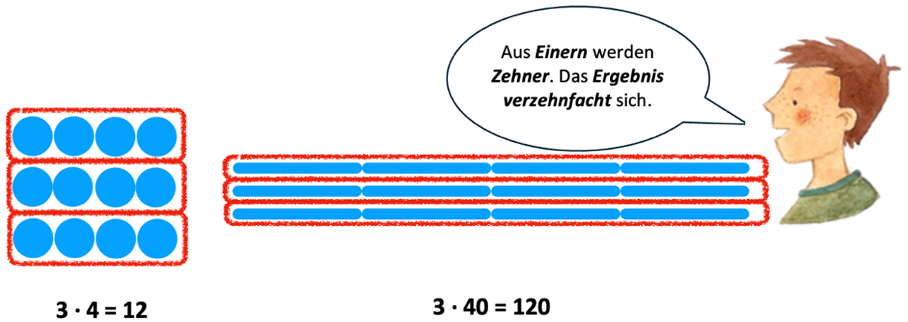
In dieser möglichen Basisaktivität untersuchen und erkunden Kinder auch Partneraufgaben und Multiplikationssets. Die Ergebnisse können selbst berechnet und notiert oder zur kognitiven Entlastung auch schon im Vorhinein auf die Multiplikationssets geklebt werden. Schließlich sollen die Kinder dazu angeregt werden, dass ihre Entdeckungen aus der Basisaufgabe auch auf die Basisaktivität zu übertragen sind. Des Weiteren beschreiben und erklären sie die Veränderungen des Ergebnisses. Dazu können die Lernenden angeregt werden mit Arbeitsaufträgen wie z. B. „Trage die Ergebnisse ein. Vergleiche die Ergebnisse. Was fällt euch auf?“
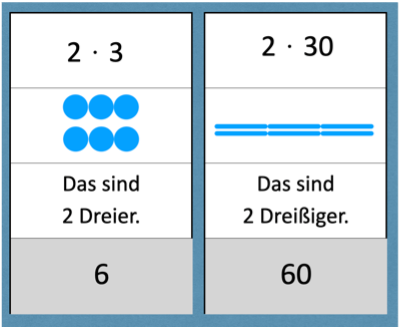
Die Kinder könnten beispielsweise begründen:
„Das Ergebnis verzehnfacht / verhundertfacht sich!“
„Es kommt immer eine Stelle mehr dazu.“
…
Basisaktivität
„Zahlbilder zeichnen“
Material: Stifte (z. B. Wachsmalstifte)


Reduktion
„Darstellungen zu den Partneraufgaben ergänzen“
Material: Unvollständige Multiplikationssets, Darstellungskarten, Forschungszettel
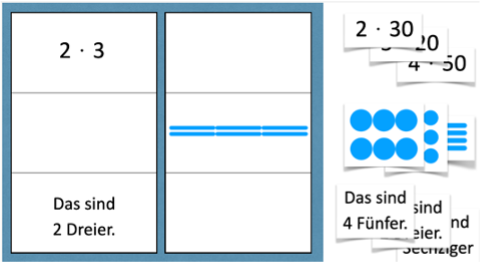
Reduktion
„Fokus auf die Kernaufgaben“
Material: Multiplikationssets und Darstellungskarten mit Kernaufgaben
Die Lernenden erkunden Malaufgaben des kleinen Einmaleins und des Zehnereinmaleins mit Bezug auf die Kernaufgaben mit 1, 2, 3, 5 und 10 und Quadrataufgaben. Sie vertiefen die Aufgaben zu den einfacher zu berechnenden Kernaufgaben und können so ebenfalls Beziehungen zwischen den Aufgaben des kleinen Einmaleins und des Zehnereinmaleins herstellen. Hierbei kann insbesondere das Legen der Aufgaben mit Material unterstützen.
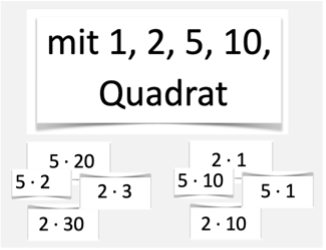
Reduktion
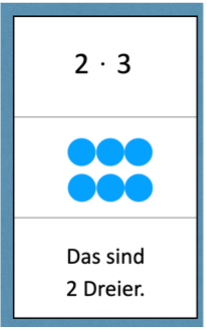
„Fokus auf Aufgaben des kleinen Einmaleins“
Material: Multiplikationssets und Darstellungskarten mit Aufgaben des kleinen Einmaleins
Erweiterung
„Darstellungen zu den Partneraufgaben legen“
Material: Leere Sets, Darstellungskarten, Forschungszettel
In dieser Erweiterung finden die Kinder selbstgewählte Partneraufgaben ohne vorausgefüllte Sets und dazu passende Darstellungskarten. Das freie Legen der Karten erhöht den Schwierigkeitsgrad, da die Kinder selbst überlegen müssen, welche Aufgaben des kleinen Einmaleins und des Zehnereinmaleins „Partner“ sein können.
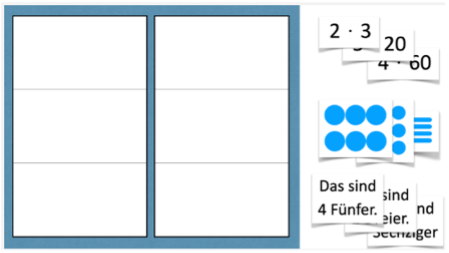
Erweiterung
„Eigene Partneraufgaben erfinden“
Material: Leere Sets, Forschungszettel
Die Kinder erfinden selbstgewählte Multiplikationssets und haben dafür keine Karten zur Verfügung. Stattdessen wählen sie selbst Multiplikationsaufgaben (und berechnen diese). Sie zeichnen das Zahlbild eigenständig, schreiben die Aufgabe in ein leeres Feld und formulieren die Erklärungen frei.

Erweiterung
„Zahlraum erweitern“
Material: Leere Sets, Darstellungskarten höherer Zahlraum, Forschungszettel
In dieser Erweiterung wird der Zahlraum – mit Fokus auf dem Stelleneinmaleins erweitert – und die Kinder finden Partneraufgaben im Zahlraum bis Hundert / Tausend. Bei Ergebnissen im großen Zahlraum kann es sein, dass eine bildliche Darstellung zu unübersichtlich wird (Beispiel: 8 ⋅ 9 vs. 8 ⋅ 90 vs. 8 ⋅ 900 „acht Neuner / Neunziger / Neunhunderter“). Dann kann an dieser Stelle darauf verzichtet werden. Wenn es jedoch anschließend darum geht, den Zusammenhang zwischen dem kleinen Einmaleins und dem Zehnereinmaleins zu verdeutlichen, ist die bildliche Darstellung (Zahlbild) eine wichtige Voraussetzung zur Beschreibung und Begründung von Zusammenhängen und das Verinnerlichen dieser.
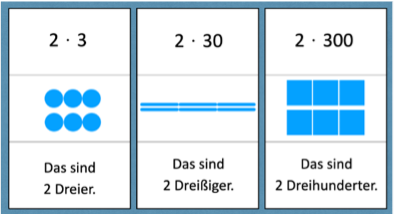
Möglichkeiten individueller Unterstützung
„Zum Aufbau mentaler Repräsentationen Material nutzen“
Material: Kopiervorlage (Einer, Zehner, Hunderter) Mehrsystemblöcke
Für den Aufbau mentaler Repräsentationen führen die Kinder aktiv Handlungen mit Material durch und legen die Aufgaben entsprechend.
Dafür können z. B. Einer, Zehner und Hunderter aus Papier genutzt werden.
Zur motorischen Unterstützung können auch z. B. Mehrsystemblöcke verwendet werden.
Zur Versprachlichung der Strukturen und dem Aufbau mentaler Repräsentationen können Impulse wie beispielsweise
„Erkläre, warum die Aufgaben 2 ⋅ 3 und 2 ⋅ 30 zu der Darstellung passen.“
„Wo siehst du… (zwei Dreißiger, zwei Dreier…)?“
gegeben werden. Der Fokus soll so auf die Strukturen der Aufgaben – hier konkret auf die Gruppen (z. B. zwei „Dreier“ und zwei „Dreißiger“) gelenkt werden.

Möglichkeiten individueller Unterstützung
„Zur kognitiven Unterstützung eine Lupe verwenden“
Material: Lupe
Zur Fokussierung und zum Hervorheben von Teilmengen des Zahlbildes (z. B. ein „Dreier“) kann eine „Lupe“ verwendet werden. Sie unterstützt das Fokussieren einer Reihe, ohne dass der Rest der Abbildung verdeckt oder weggenommen wird. Außerdem lenkt dieses Vorgehen die Aufmerksamkeit auf die Stelle, die beachtet werden soll.
Durch den Einsatz der „Lupe“ soll die Bündelung der Einer und der Zehner in einer Reihe deutlich gemacht werden. Diese kann sowohl bei der Beschreibung der Aufgaben als auch beim Vergleich von Partneraufgaben genutzt werden, um einen Bezug herzustellen.
Zur Erstellung der Lupe können z. B. aus farbigen Prospekthüllen Malwinkel erstellt werden (s. Abbildung 16).

Möglichkeiten individueller Unterstützung
„Zur sprachlichen Unterstützung einen Sprachspeicher nutzen.“
Material: Sprachspeicher
Das Beschreiben der Darstellungen kann durch das Anlegen eines Sprachspeichers unterstützt werden (vgl. hierzu auch Förderschwerpunkt Sprache: Unterricht; Leitideen: Austausch anregen). Ein Sprachspeicher kann die Kinder bei einer Verwendung von Fachsprache unterstützen und gemeinsam in der Klasse entwickelt werden.
Mögliche Begriffe / Satzbausteine, die zum Thema Zehnereinmaleins sprachlich unterstützen können, sind:
Sprachspeicher
Wörter (z. B.)
- Einer, Zweier, Dreier, …
- Zehner, Zwanziger, Dreißiger, …
- verzehnfachen
- Reihe/n
- Zehnereinmaleins, Einmaleins
- Multiplikation, multiplizieren, mal
- Division, dividieren, geteilt, teilen
- Umkehraufgabe
- …

Satzbausteine (z. B.):
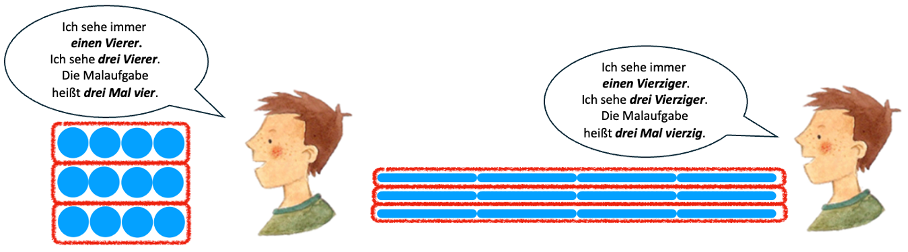
Abbildung 18: Satzbausteine: Multiplikationsdarstellungen beschreiben