Gemeinsames Lernen mit Hilfe offener Aufgabenstellungen – Die vielfältigen Einsatzmöglichkeiten von offenen Aufgaben im inklusiven Unterricht sinnvoll nutzen
Offene Aufgabenstellungen können an verschiedenen Stellen, in nahezu jedem Themengebiet eingesetzt werden, weshalb im Folgenden darauf verzichtet wird, den Fokus auf eine spezielle Unterrichtsreihe zu richten. Auf Grundlage unterschiedlicher Unterrichtsbeispiele verschiedenster Themengebiete sollen die drei Abschnitte verdeutlichen, wann der Einsatz offener Aufgaben besonders sinnvoll ist und wie sie, richtig angewendet, in inklusiven Lerngruppen einen Lerneffekt nach sich ziehen können.
Offene Aufgaben als Türöffner und Diagnoseinstrument
Zu Beginn einer Unterrichtsreihe eignen sich offene Aufgaben häufig dazu, Schülerinnen und Schüler mit dem neuen Lerninhalt zu konfrontieren („Türöffner“). Die Kinder können unvoreingenommen Ideen entwickeln, um so einen eigenen Zugang zum neuen Thema zu bekommen (vgl. Rasch, 2004). Zugleich können offene Aufgaben für die Lehrkräfte gerade zu Beginn aufschlussreich sein, da sichtbar wird, welche Vorkenntnisse die Lernenden schon mitbringen. Sie können somit zugleich als diagnostisches Instrument zur Lernstandsfeststellung dienen (Eingangs- und Abschlussstandortbestimmung, vgl. Sundermann & Selter, 2006).
Das gleiche Dokument kann zum Anfang und zum Ende einer Unterrichtsreihe eingesetzt werden, wodurch nicht nur die Lernvoraussetzungen, sondern auch der Lernprozess in den Blick genommen wird. Dies ist bei der großen Heterogenitätsspanne von Lernvoraussetzungen in inklusiven Lerngruppen von besonderer Bedeutung. Dadurch wird nicht nur der Lehrkraft, sondern auch dem Kind selbst verdeutlicht, welchen Lernfortschritt es innerhalb eines Themas machen konnte. Die folgenden Kinderdokumente wurden zu Beginn und zum Abschluss einer geometrischen Unterrichtsreihe zu „Figuren und Formen“ von den Kindern erstellt.
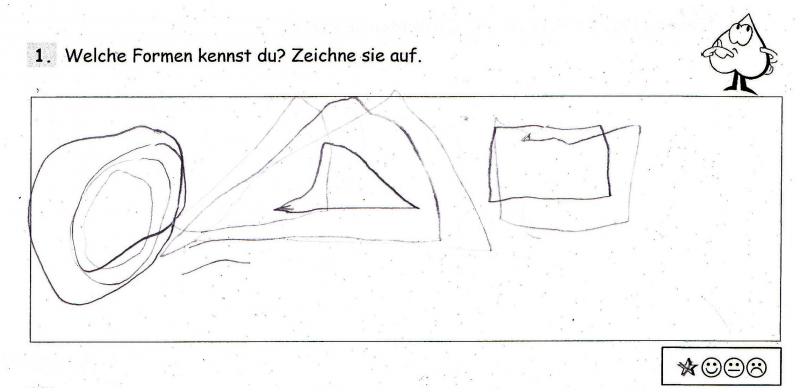 Abbildung 9
Abbildung 9
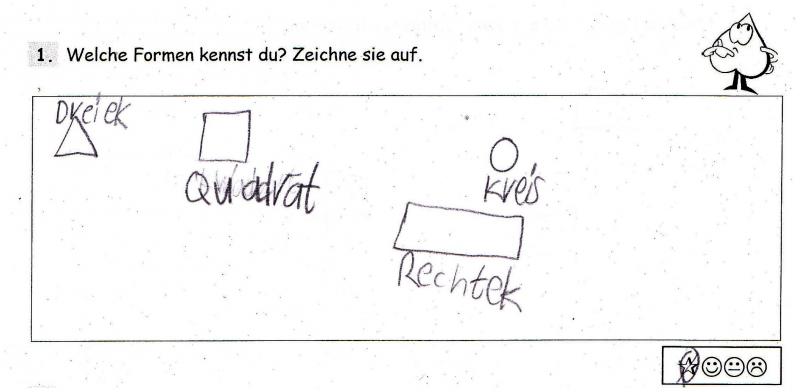 Abbildung 10
Abbildung 10
Durch eine offene Aufgabe als Standortbestimmung werden für die Lehrkraft die unterschiedlichen Voraussetzungen erkennbar, wodurch wiederum Rückschlüsse zur Planung der bevorstehenden Unterrichtsreihe gezogen werden können (vgl. ‚Diagnosegeleitet fördern‘). Die Kinderdokumente (Abb. 9; Abb.10) verdeutlichen, wie groß die Leistungsunterschiede der beiden Lernenden sind. Trotzdem konnten beide Kinder die Aufgabe bearbeiten, da sie anders als bei geschlossenen Aufgaben nicht entmutigt wurden und in der Konsequenz möglicherweise etwas Falsches zeichneten.
Auch das Mädchen mit Unterstützungsbedarf (Abb. 9) kreuzte bei der Selbsteinschätzung das Sternsymbol an, wodurch sie ausdrückt, das Gefühl zu haben, die Aufgabe gut bewältigt zu haben. Wenn die Aufgabenstellungen geschlossener gewesen wären, wie beispielsweise „Zeichne ein Quadrat.“ oder „Zeichne ein Rechteck.“ usw., wäre ein Großteil der Lernenden in dieser Lerngruppe vermutlich überfordert gewesen.
Offene Aufgaben zur Vertiefung von bereits Erarbeitetem
Auch innerhalb von Unterrichtsreihen können offene Aufgabenstellungen eingesetzt werden, um bereits Erarbeitetes zu vertiefen oder Inhalte zu automatisieren, den Kindern aber zugleich Freiraum bei der Bearbeitung zu lassen (vgl. Nührenbörger & Verboom, 2005).
Um beispielsweise verschiedene Rechenwege am Rechenstrich zu vertiefen, erhielten die Schülerinnen und Schüler bei einer Unterrichtsreihe zum Thema „Wir rechnen am Rechenstrich“ (vgl. ‚Verwandte Aufgaben‘) ein sogenanntes Probierblatt (vgl. Arbeitsblatt „Probierblatt Rechenstrich“). Dieses Blatt enthielt lediglich leere Rechenstriche, auf denen die Lernenden den Zahlenraum, die Strategien und die (in diesem Fall) Additionsaufgaben selber wählen konnten.
 Abbildung 11
Abbildung 11
 Abbildung 12
Abbildung 12
Obwohl die Kinder bereits im zweiten Schuljahr sind, zeigte sich, dass manche Kinder das Rechnen im Zahlenraum bis 20 noch bevorzugten (Abb. 11), während andere einen höheren Zahlenraum (Abb. 12) zum Rechnen wählten. Auch die angewendeten Strategien waren unterschiedlich. Während der Schüler in Abbildung 11 seine gestellte Aufgabe eher durch Ausprobieren löste, ging der Schüler in Abbildung 12 schon systematischer vor und nutzte gleich mehrere Strategien (Ergänzen zum Zehner, Aufteilung in Einer und Zehner mit Zuhilfenahme der „Kraft der Fünf“).
Diese unterschiedlichen Ergebnisse zeigen, dass sich derartige Aufgaben eignen, um die verschiedenen Lernvoraussetzungen von Kindern innerhalb einer Aufgabenstellung zu berücksichtigen. Da es bei der Präsentation im Plenum nicht um das Ausrechnen bestimmter Aufgaben, sondern um das Vorstellen von Rechenwegen ging, konnte eine gemeinsame Reflexion stattfinden, an der sich alle Kinder beteiligen konnten.
Offene Aufgaben können zudem helfen, Inhalte wie beispielsweise Aufgaben des kleinen Einmaleins zu automatisieren. Bei den folgenden Beispielen durften die Kinder Einmaleins-Aufgaben bilden und rechnen (vgl. Arbeitsblatt „Eigene Malaufgaben“). Diese sortierten sie dann zusätzlich in „leichte und schwere Aufgaben“.
 Abbildung 13
Abbildung 13
 Abbildung 14
Abbildung 14
Auch diese offene Aufgabenstellung ermöglichte es jedem Kind, die Aufgabe zu bearbeiten. Der Schüler mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ (Abb. 13) nahm eine andere Sortierung vor als der Regelschulschüler (Abb. 14). Dennoch konnten beide die Aufgabe entsprechend ihrer Möglichkeiten bearbeiten.
Offene Aufgaben zur Anregung der Kreativität
Offene Aufgaben, insbesondere Eigenproduktionen wie beispielsweise „Erfinderaufgaben“ (vgl. Sundermann & Selter, 2006), können helfen, die prozessbezogenen Kompetenzen „Problemlösen/kreativ sein“ anzuregen (vgl. MSW, 2008).
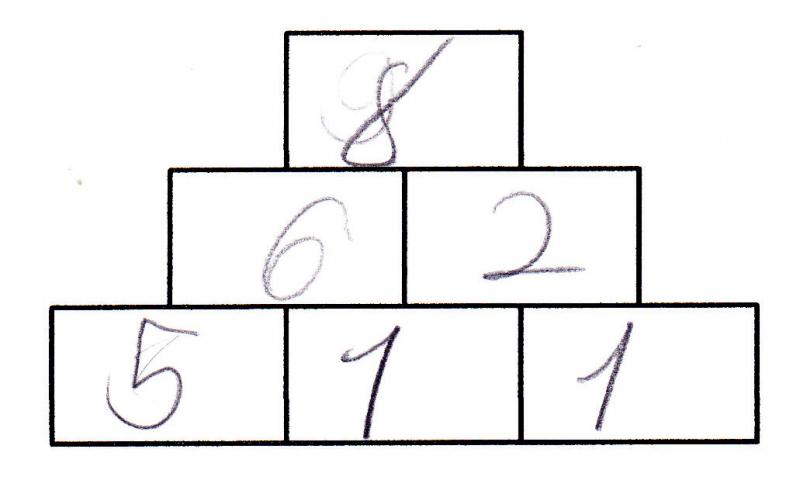 Abbildung 15
Abbildung 15
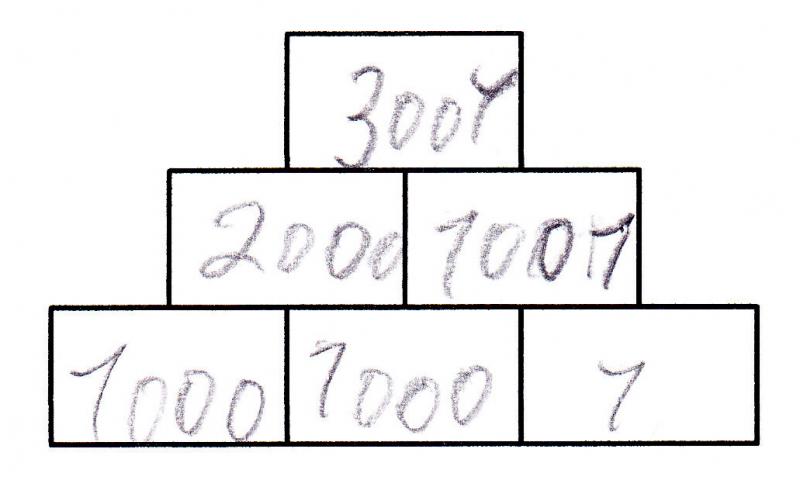 Abbildung 16
Abbildung 16
Mit einer Aufgabenstellung wie etwa „Erfinde eigene Zahlenmauern“ (vgl. Arbeitsblatt „Zahlenmauern erfinden“) vertiefen die Lernenden nicht nur das Rechnen mit dem Aufgabenformat, sondern werden zugleich in ihrer Kreativität gefördert, indem sie beispielsweise eigene Zahlenwerte auswählen. Dabei können sie eigene Grenzen ausprobieren, aber auch überschreiten (vgl. Nührenbörger & Verboom, 2005). Gerade in inklusiven Lerngruppen fallen die Ergebnisse solcher Aufgabentypen sehr unterschiedlich aus, wie Abbildung 15 und 16 veranschaulichen. Ein großer Vorteil ist hierbei die problemlose Übertragbarkeit auf andere Aufgabenformate wie Rechenketten, Rechendreiecke, Entdeckerpäckchen etc. (vgl. ‚Tipps und Herausforderungen‘).
 Abbildung 17
Abbildung 17
 Abbildung 18
Abbildung 18
Auch im größeren Rahmen können „Erfinderaufgaben“ als offene Aufgaben gestellt werden. Gegen Ende einer Unterrichtsreihe zum Thema „Entdeckerpäckchen“ (vgl. PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichtsmaterial – Entdeckerpäckchen) wurde den Kindern die Aufgabe gestellt, eigene Arbeitsblätter zum Thema zu entwickeln. Einige Kinder (Abb. 17) nutzen ein bereits im Unterricht thematisiertes Arbeitsblatt als Vorlage, während leistungsstärkere Kinder (Abb. 18) eigene Zahlwerte und Variationen (höherer Zahlenraum, verschiedene Erhöhungen von erster/zweiter Zahl) wählten. Auch diese offene Aufgabenstellung ist problemlos auf andere Unterrichtsreihen und Aufgabenformate übertragbar.
Weitere Anregungen
Die Produktionen der Kinder (z.B. Abb. 17; Abb. 18) können überdies auch zur Gestaltung der weiteren Unterrichtsprozesse genutzt werden, indem die selbst erfundenen Arbeitsblätter in der Mathe-Ecke für die anderen Schülerinnen und Schüler (oder auch der Parallelklasse) zur Verfügung gestellt werden. Dies ist bei vielen offenen Aufgaben möglich und für die Kinder zugleich ein sinnstiftender und damit motivierender Kontext. Auch beim Einführen von Klassenarbeiten ist es sinnvoll, die Lernenden in den Entstehungsprozess miteinzubeziehen und eigene Klassenarbeiten erstellen zu lassen (vgl. Abb. 19; PIKAS: Haus 10: Beurteilen und Rückmelden – Unterrichtsmaterial – Mathearbeiten wie die Großen!).
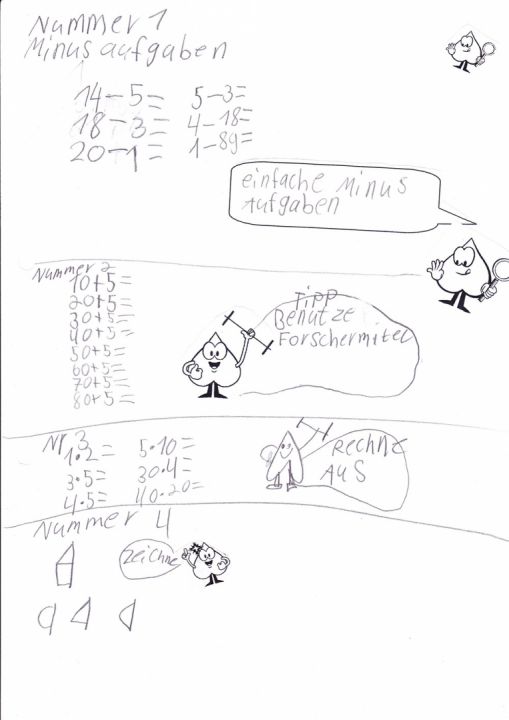 Abbildung 19: Eigene Klassenarbeit
Abbildung 19: Eigene Klassenarbeit
Beispielhafte Anregungen, wie „geschlossene" Mathematikaufgaben auf verschiedene Arten geöffnet werden können, finden Sie unter Anregungen zum Öffnen von Mathematikaufgaben:
Anregungen zum Öffnen von Mathematikaufgaben