Gemeinsames Lernen durch Nutzung und Vernetzung unterschiedlicher Darstellungsformen – eine handlungsorientierte Auseinandersetzung mit Quadratmehrlingen unter Berücksichtigung individueller Zugänge
Das nachfolgende Beispiel entstammt einer geometrischen Unterrichtsreihe zum Thema „Polyominos“ (Quadratmehrlinge). Polyominos sind ebene Figuren, die durch das Aneinanderlegen von kongruenten Quadraten auf der Grundlage bestimmter Legeregeln entstehen. Benachbarte Quadrate müssen mindestens eine gemeinsame Seite aufweisen d.h. sie dürfen nicht nur an einer Ecke anliegen und dürfen sich nicht überlappen (vgl. MSW, 2008b; s. Abb 6).
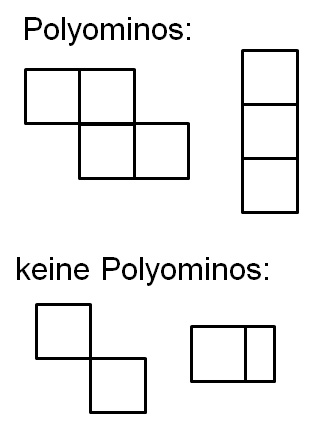 Abbildung 6
Abbildung 6
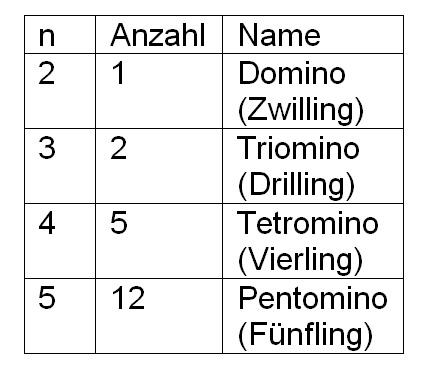 Abbildung 7
Abbildung 7
Der einfachste Repräsentant ist der aus einem Quadrat bestehende Einling. Durch Aneinanderlegen von Quadraten entstehen ein Zwilling, zwei Drillinge, fünf Vierlinge, zwölf Fünflinge usw. (vgl. Schipper, 2009; s. Abb.7).
Zu beachten ist außerdem, dass bei der Anzahlbestimmung der voneinander verschiedenen Polyominos Symmetrie- und Kongruenzeigenschaften miteinbezogen werden (vgl. Müller & Wittmann, 2013). Die Bestimmung von Polyominos durch Anwendung der genannten Legeregeln setzt voraus, dass das Quadrat als geometrische Figur erkannt und seine Eigenschaften benannt werden können. Die Planung der Reihe knüpft mit der Untersuchung eines Quadrates und dem Aufbau von Grundwissen an dieser Stelle an.
Die handlungsorientierte und aktiv-entdeckende Auseinandersetzung mit Polyominos soll die Raumvorstellung der Kinder fördern und die Problemlösefähigkeit erweitern, indem die Lernenden Strategien zum Auffinden von Quadratmehrlingen entdecken, beschreiben und deren Nutzen erkennen sowie ihre entwickelten Strategien auf weiterführende und selbsterzeugte Aufgaben übertragen. Das Nutzen unterschiedlicher Darstellungsformen erleichtert diesen Vorgang erheblich, da sie den Lernenden viel Freiheit bei der Lösungssuche geben.
So zeigt eine genauere Untersuchung der nachfolgenden Kinderdokumente, wie Kinder auf unterschiedlichen Niveaustufen einen Lernerfolg erzielen konnten. Die gezeigten Dokumente der durchgeführten Unterrichtsreihe stammen aus einer aus 30 Schülerinnen und Schülern bestehenden zweiten Schulklasse mit sehr heterogenen Lernvoraussetzungen. In der inklusiven Lerngruppe befinden sich u.a. Kinder mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ und sonderpädagogischem Unterstützungsbedarf im „sozial-emotionalen Bereich“ sowie im Bereich „Sprache“. Die Klasse weist zudem einen hohen Anteil von Kindern auf, die Deutsch als Zweitsprache lernen.
Die dargestellte Unterrichtsstunde hat das Thema „Wir erforschen Zwillinge und Drillinge“, in der das Kernanliegen (der initiierte/bewusste Lernzuwachs am Ende der geplanten Unterrichtsstunde) darin besteht, selbstständig alle möglichen Drillinge unter Verwendung von vereinbarten Legeregeln (s. Abb. 8) zu finden, um die Lernenden für eine systematische Auffindung weiterer Polyominos im Verlauf der Unterrichtsreihe zu sensibilisieren.
 Abbildung 8
Abbildung 8
Um die Anzahlen von Polyominos eindeutig bestimmen zu können, ist das Anwenden einer Systematik erforderlich. Die Lernenden sollten an die Erkenntnis herangeführt werden, dass ein systematisches Vorgehen, vor allem bei erhöhter Quadratanzahl, von entscheidender Bedeutung ist. Grundsätzlich können dabei zwei Methoden zum Einsatz kommen: Eine Möglichkeit ist die Konstruktionsmethode, bei der der Domino als Basis benutzt wird, um durch Anlegen eines weiteren Quadrats die beiden Triominos zu bestimmen. Die andere Möglichkeit ist die Herleitung mit Hilfe eines Kreislaufs, bei der ein Quadrat eines gefundenen Triominos nach einer gefundenen Lösung verschoben wird (vgl. Albrecht-Bühler, 1992) woraufhin von allen gleichen Quadratmehrlingen außer ein Exemplar die anderen aussortiert werden (Für nähere Informationen s. auch PIKAS: Haus 7: Gute Aufgaben – Unterrichtsmaterial – Pentominos)
Der Auftrag „Finde möglichst schlau verschiedene Drillinge. Zeichne/Beschreibe deinen Trick.“ verdeutlicht bereits, dass kein Zugang vorgegeben ist. Die Kinder hatten die Möglichkeit, diesen Auftrag durch Aufzeichnen, Aufschreiben oder durch Handlung am Material (s. Abb. 9) durchzuführen.
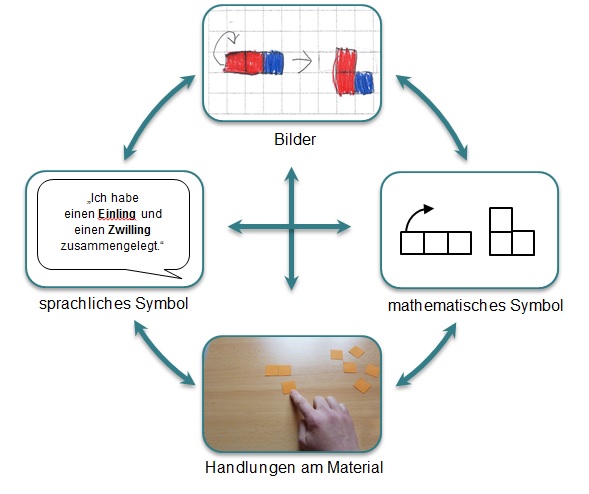 Abbildung 9
Abbildung 9
Um auch den Kindern mit Schwierigkeiten im sprachlichen Bereich (vgl. ‚Förderschwerpunkt Sprache') die sprachlich-symbolische Darstellungsform unter Verwendung von Fachsprache zu ermöglichen, sollte ein Wortspeicher (Abb. 10) als Unterstützung zur Verfügung stehen (vgl. PIKAS: Haus 4: Sprachbildung – Fortbildungsmaterial – Grundlegendes).
 Abbildung 10
Abbildung 10
Zur Bewältigung der Aufgabenstellung standen den Kindern zwei analog aufgebaute Arbeitsblätter (Abb. 11) sowie das entsprechende Material (vgl. Vorlage „Pappquadrate klein“) zur Verfügung. Im Fokus stand nicht die Anzahl der gefundenen Drillinge, sondern die dazu benötigten Tricks. Im Idealfall sollten diese eine Systematik aufweisen, die den Kindern auch beim Finden von Vierlingen, Fünflingen etc. behilflich sein könnte.
 Abbildung 11: Arbeitsblätter „Wir erforschen Quadratlinge“
Abbildung 11: Arbeitsblätter „Wir erforschen Quadratlinge“
Die Kinder haben die Problemstellung sehr unterschiedlich bearbeitet. Viele Schülerinnen und Schüler nutzten zunächst die Möglichkeit mit Pappquadraten Drillinge durch „Probieren“ zu legen, bevor sie zur Beschreibung eines Tricks übergingen. Kinder, die am Material gehandelt haben, hatten zudem die Möglichkeit, ihre gefundenen Figuren an der Stelle aufzukleben, wo die anderen zeichneten (vgl. Abb. 12 oben), um ihre Ergebnisse im gemeinsamen Austausch mit den Mitschülerinnen und Mitschülern auch fixiert zu haben. Abbildung 12 zeigt das Vorgehen eines leistungsschwächeren Kindes, welches mit Quadraten gehandelt hat und ebendies später auch als Trick („Ich habe Quadrate genommen“) bezeichnete. Es wird deutlich, dass es lediglich beim Ausprobieren geblieben ist, da zu diesem Zeitpunkt noch kein systematisches Vorgehen erkennbar war.
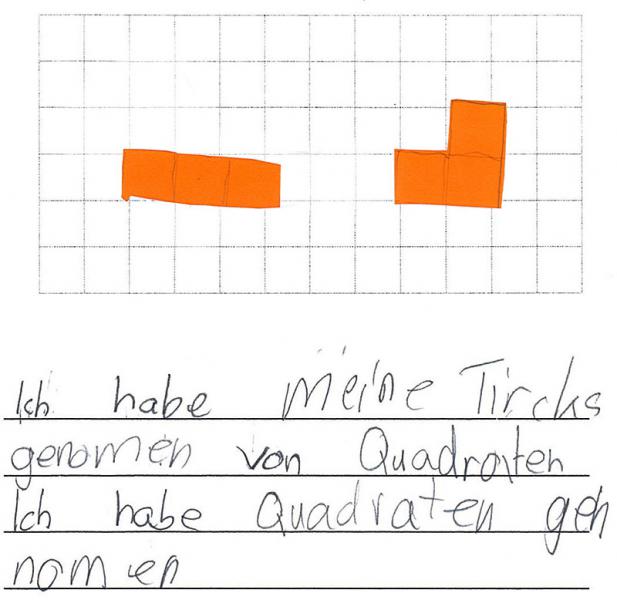 Abbildung 12
Abbildung 12
Ein Mädchen mit Unterstützungsbedarf im Bereich „Sprache“ entschied sich dafür, mit Material zu handeln und den gefundenen Trick daraufhin aufzuzeichnen. Als Darstellungshilfe nutzte sie die „Forschermittel“ Pfeile (vgl. ‚Forschermittel‘), welche ihr dazu verhalfen, den gefundenen Trick für die anderen Kinder zu veranschaulichen (Abb. 13).
 Abbildung 13
Abbildung 13
Auch ein mathematisch leistungsstarkes Kind nutzte diesen bildlichen Zugang, da das kürzlich aus Polen immigrierte Mädchen nur sehr geringe Deutschkenntnisse hat (vgl. Abb. 14). Durch die farbige Markierung wird zudem deutlich, wie aus dem einen Drilling durch Verschieben eines Quadrates ein anderer entstanden ist.
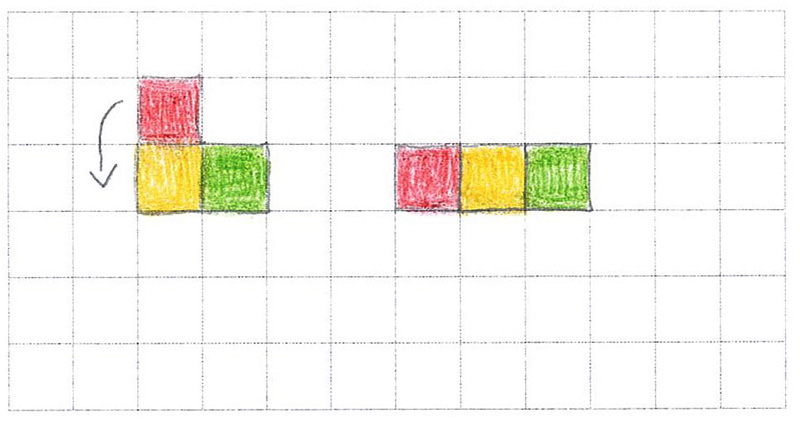 Abbildung 14
Abbildung 14
Bei beiden Schülerinnen ist zu erkennen, dass sie zunächst einen Drilling aus drei einzelnen Quadraten gelegt und daraufhin ein Quadrat verschoben haben, um einen weiteren Drilling zu finden. Dies entspricht der aus der Literatur bekannten Kreislauf-Methode (vgl. Albrecht-Bühler, 1992).
Die meisten Kinder entschieden sich für die Möglichkeit, den Trick zu zeichnen und anschließend schriftlich zu beschreiben. Abbildung 15 zeigt das Vorgehen eines leistungsschwächeren Kindes, welches die induktive Konstruktionsmethode anwendete. Aus der Beschreibung wird deutlich, dass als Ausgangslage ein Domino genutzt wurde, welchem ein einzelnes Quadrat hinzugefügt wurde. Die Nutzung von Fachsprache ist bei diesem Kind noch nicht sehr ausgeprägt. Zudem kann das Vorgehen nicht verallgemeinert werden, da der Trick als „Drilling-Trick“ bezeichnet wird.
 Abbildung 15
Abbildung 15
 Abbildung 16
Abbildung 16
Das Mädchen mit Unterstützungsbedarf im Bereich „Sprache“ wendete den gleichen Trick an und versuchte diesen mit Zuhilfenahme des Wortspeichers zu beschreiben (Abb. 16).
Am häufigsten wurde von den Kindern die Kreislauf-Methode genutzt. Das Mädchen (Abb. 17) konnte ihr Vorgehen schon gut bildlich veranschaulichen und sprachlich beschreiben, aber den Trick noch nicht benennen bzw. verallgemeinern.
 Abbildung 17
Abbildung 17
Anders war dies bei einem leistungsstärkeren Kind (Abb. 18). Das Dokument zeigt die Kreislauf-Methode, welche vom Schüler durch entsprechende Farben (hinzugefügtes Quadrat in rot) und den Pfeil (Verschiebung) gut veranschaulicht wurde. Auch die Bezeichnung des „Tricks“ ist schon allgemein („Schiebetrick“).
 Abbildung 18
Abbildung 18
Ähnliches war bei einem anderen Kind zu beobachten (Abb. 19). Die Verwendung von Fachsprache und die Verallgemeinerung des „Tricks“ sind hier feststellbar.
 Abbildung 19
Abbildung 19
Abbildung 20 und 21 zeigen die Arbeitsblätter eines Mädchens, welche gleich beide Tricks entdeckte und zwei Arbeitsblätter in der Unterrichtsstunde bearbeitete. Sie nutzte die Fachwörter aus dem Wortspeicher und veranschaulichte die induktive Konstruktionsmethode durch unterschiedliche Farben des Quadrats und des Dominos (Abb. 20).
 Abbildung 20
Abbildung 20
Auch beim Beschreiben der Kreislauf-Methode nutzte sie Fachwörter und veranschaulichte diese durch einen Pfeil (Abb. 21; vgl. ‚Forschermittel‘).
 Abbildung 21
Abbildung 21
Am Ende der Stunde wurden die verschiedenen Tricks im Plenum vorgestellt und anhand großer Pappquadrate (vgl. Vorlage „Pappquadrate groß“) veranschaulicht. Ein gemeinsamer Austausch war problemlos möglich. Alle Kinder konnten, unabhängig von ihren Lernvoraussetzungen, ihre „Tricks“ visualisieren und vorstellen. Wo leistungsschwächere Kinder ihre gefundenen Drillinge durch Legen großer Pappquadrate darstellten, konnten leistungsstärkere Lernende unvollständige Beschreibungen ergänzen oder die vorgestellten exemplarischen Ergebnisse verallgemeinern. So erhielten auch die leistungsschwächeren Kinder Einblicke in ein systematisches Vorgehen und konnten dieses Wissen in den darauffolgenden Stunden zum Finden von Vier- bzw. Fünflingen nutzen. Die erzeugte Kommunikation untereinander initiierte nebenbei einen ständigen Wechsel der Darstellungsformen.
Weitere Anregungen
Die Vorgehensweisen zum Auffinden der Drillinge sollten den Lernenden die benötigten Impulse geben, in den folgenden Unterrichtsstunden unter Anwendung einer Strategie alle Vier- bzw. Fünflinge zu finden. Fast alle Kinder gingen beim Auffinden der Vierlinge nun systematisch vor (Abb. 22).
 Abbildung 22
Abbildung 22
Beispielhaft soll in Abbildung 22 verdeutlich werden, wie der „Schiebetrick“ (Kreislauf-Methode) von den Kindern auf das Finden der Vierlinge übertragen wurde. Auch die induktive Konstruktionsmethode wurde von einigen Kindern angewendet. Ein Junge nutzte die zwei verschiedenen Drillinge und legte jeweils zu einem Drilling immer ein Quadrat hinzu, wodurch er verschiedene Vierlinge erzeugte (Abb. 23).
 Abbildung 23
Abbildung 23
Nach der Bestimmung der Quadratmehrlinge folgte eine Vertiefung der Kenntnisse, indem die Lernenden mithilfe der gefundenen Polyominos Umrissfiguren legten und eigene Aufgaben erfanden, die von den Mitschülerinnen und Mitschülern gelöst werden sollten (Abb. 24). Die Erstellung einer eigenen Rätselkartei (vgl. Vorlage „Rätselkartei“) – als zu erzeugendes Handlungsprodukt – bettet die Unterrichtsreihe in einen sinnstiftenden und authentischen Kontext ein (vgl. Bartnitzky et al., 2009; vgl. Abb. 24) und erhöht zugleich die Motivation der Kinder.
 Abbildung 24
Abbildung 24
Abschließend ist noch anzumerken, dass themenunabhängig darauf geachtet werden sollte, Aufgaben so zu stellen, dass unterschiedliche Darstellungsformen zugelassen bzw. unterschiedliche Zugänge angesprochen werden.
Durch die dokumentierte Unterrichtsreihe wird deutlich, wie unterschiedlich die Schülerinnen und Schüler an die Aufgabenstellung herangegangen sind. Jedes Kind begann die Suche nach Strategien mit der ihm am sinnvollsten erscheinenden Darstellungsform und kam so zu einem zufriedenstellenden Ergebnis. Insbesondere die anschließende Interaktion mit anderen Lernenden ermöglichte zugleich, die eigenen Strategien mit anderen abzugleichen, wodurch eine Vernetzung der unterschiedlichen Darstellungsformen initiiert wurde.
Durch die Wahl von Aufgabenstellungen, die unterschiedliche Darstellungsformen bzw. Zugänge zulassen, kann man demnach – ganz themenunabhängig – die prozessorientierten Kompetenzen von Schülerinnen und Schülern fördern. Eine Beschränkung der Aufgabenlösung auf eine einzelne Darstellungsform sollte daher – wann immer es möglich ist – vermieden werden.