Die Bearbeitung einer Aufgabenstellung sollte durch die Bereitstellung unterschiedlicher Zugänge sowie die Nutzung und Vernetzung verschiedener Darstellungsformen (Abb. 4) erleichtert werden. In der Mathematikdidaktik wird häufig zwischen vier verschiedenen Darstellungsformen unterschieden: Handlungen am Material, bildliche Darstellungen, mathematisch-symbolische Darstellungen und sprachlich-symbolische Darstellungen (s. Abb. 4).
Jeder mathematische Sachverhalt kann durch verschiedene Darstellungsformen ausgedrückt werden. Ausgehend von einer Darstellungsform ist es möglich, diesen Sachverhalt in eine andere Form zu übersetzen (blaue Pfeile). Da alle Darstellungsformen aber auf rein mathematischen Begriffen und Strukturen basieren, die physisch nicht fassbar sind, bedarf es verschiedener Darstellungsmittel (Abb.5) wie beispielsweise didaktisches Material oder Symbole, um das Gemeinte zu veranschaulichen vgl. PIKAS: Unterrichtsanregungen zur Förderung des Darstellungswechsels
Auch innerhalb einer Darstellungsform können durch die Zuhilfenahme unterschiedlicher Darstellungsmittel Wechsel z.B. zwischen verschiedenen bildlichen Darstellungen stattfinden (braune Pfeile; vgl. Kuhnke, 2012).
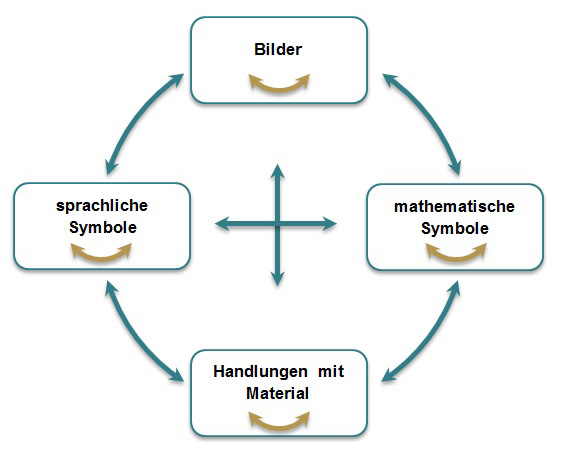 Abbildung 4: „Darstellungsformen“
Abbildung 4: „Darstellungsformen“
Weitere Informationen sowie ein ähnliches Modell sind auch bei PIKAS zu finden (vgl. PIKAS: Haus 3: Rechenschwierigkeiten – Informationsmaterial).
Zur Illustration:
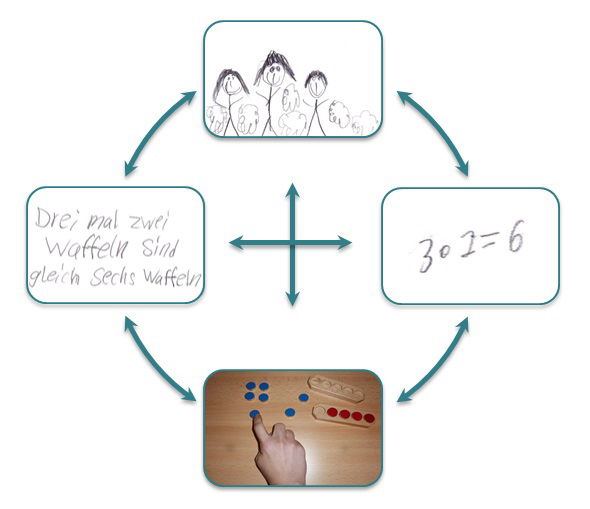 Abbildung 5: „Darstellungsmittel“
Abbildung 5: „Darstellungsmittel“
Ein und derselbe Sachverhalt kann also durch unterschiedliche Darstellungsformen mit Hilfe verschiedener Darstellungsmittel anders veranschaulicht werden (s. Abb. 5). So kann das Ergebnis der Rechengeschichte (vgl. Einstieg) etwa durch die mathematischen Symbole 3·2=6, durch geschriebene oder gesprochene sprachliche Symbole („Drei mal zwei Waffeln sind sechs Waffeln.“), als Bild oder im Falle der Materialhandlungen auch mit verschiedenen Darstellungsmitteln bspw. durch Plättchen oder Kastanien dargestellt werden.
Das Nutzen von verschiedenen Darstellungsformen und -mitteln wird in den Kompetenzformulierungen des Lehrplans NRW aufgeführt, in denen es heißt: „Schülerinnen und Schüler wechseln zwischen verschiedenen Darstellungsformen von Operationen (mit Material, bildlich, symbolisch, sprachlich) hin und her bzw. können diese übertragen“ (MSW, 2008a, S. 61).
Als zentrale Leitidee wird zudem explizit auf das Vernetzen verschiedener Darstellungen hingewiesen (vgl. MSW, 2008a).
Die Beherrschung verschiedener Darstellungsformen ist ein wichtiger Indikator für die mathematischen Kompetenzen eines Kindes. Je flexibler es zwischen solchen Darstellungen wechseln kann, desto leichter fällt ihm das Lösen komplexer mathematischer Probleme, da es die jeweilige Aufgabenstellung aus verschiedenen Blickwinkeln betrachten kann. Beschränkt sich ein Kind auf eine Darstellungsform, kann dies der eigenen Problemlösekompetenz im Weg stehen und in späteren Schuljahren das Lösen komplexerer Aufgaben erschweren.
Ein frühzeitiges Erkennen dieser Schwierigkeiten, wie beispielsweise bei Mark aus unserem Anfangsbeispiel, kann durch die Wahl geeigneter Aufgabentypen und durch das Üben von Darstellungswechseln entgegengewirkt werden (vgl. Kuhnke, 2012; vgl.
PIKAS: Unterrichtsanregungen - DarstellungswechselUm das Nutzen aller Darstellungsformen zu initiieren, müssen Aufgabenstellungen entsprechend gewählt, Material als Lern- und Kommunikationshilfe bereitgestellt und Zugänge durch Darstellungshilfen (vgl. ‚Forschermittel‘) erleichtert werden.
Das Vollziehen von Darstellungswecheln, beispielsweise vom mathematischen Symbol in ein Bild, ist Voraussetzung für ein solides Zahl- und Operationsverständnis, wie etwa die Grundvorstellungen der Multiplikation (vgl. Wartha & Schulz, 2014; vgl. Schipper, 2013). Bleibt es allein bei einer Bearbeitung auf symbolischer Ebene, können zwar Regeln und Definitionen vermittelt aber keine Grundvorstellungen aktiviert werden. Dies geschieht erst, wenn eine Erklärung sowohl am Material als auch symbolisch vorgenommen werden kann (vgl. Wartha & Schulz, 2014).
Kinder bringen nicht nur unterschiedliche Voraussetzungen bezüglich ihrer mathematischen Kompetenzen mit, sondern bearbeiten ein und dieselbe Aufgabenstellung häufig durch das Nutzen unterschiedlicher Darstellungsformen. Es ist daher auch nicht zu erwarten, dass der Darstellungswechsel von allen Schülerinnen und Schülern in ähnlicher Weise automatisch vollzogen wird (vgl. Kuhnke, 2012). Um individuelle Zugänge, zugleich aber auch einen gemeinsamen Austausch zu ermöglichen, sollten Aufgaben daher auch das Vernetzen unterschiedlicher Darstellungsformen zulassen.