Gemeinsames Lernen mit Hilfe paralleler Aufgaben – Das Erforschen des Hunderterraumes auf Grundlage inhaltlich analoger Aufgabenstellungen
Das folgende Unterrichtsbeispiel entstammt einer Unterrichtsreihe zur Zahlenraumerweiterung bis 100 („Wir erforschen die Hundertertafel“), die in einer aus 30 Schülerinnen und Schülern bestehenden zweiten Schulklasse mit sehr heterogenen Lernvoraussetzungen durchgeführt wurde. In der inklusiven Lerngruppe befinden sich u.a. Kinder mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ und sonderpädagogischem Unterstützungsbedarf im „sozial-emotionalen Bereich“ sowie im Bereich „Sprache“. Der Schwerpunkt lag auf der aktiv-entdeckenden Auseinandersetzung mit dem Medium „Hundertertafel“ (Abb. 4; vgl. Wittmann & Müller, 1993) und ihrer dezimalen Zahldarstellung.
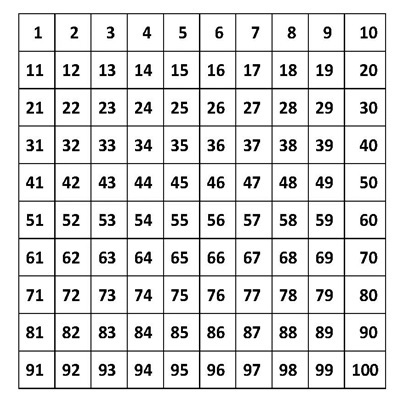 Abbildung 4: „Hundertertafel"
Abbildung 4: „Hundertertafel"
Die Zahlen von 1 bis 100 sind systematisch dargestellt, wobei der ordinale Zahlaspekt im Vordergrund steht. Jede Zahl hat innerhalb der vorgegebenen dezimalen Struktur ihren festen Platz (vgl. Nührenbörger & Pust, 2006).
Die „Hundertertafel“ bietet sich für verwandte Aufgabenstellungen an, da sich die Aufgaben innerhalb des Mediums bezüglich der Schwierigkeitsanforderungen vielfältig differenzieren lassen (vgl. Lorenz & Radatz, 1993) und jedes Kind etwas entdecken kann.
Das Kernanliegen (der initiierte/bewusste Lernzuwachs) der Unterrichtsreihe bestand zum einen darin, mathematische Strukturen innerhalb des erweiterten Zahlenraums bis 100 zu entdecken, zu beschreiben und zu begründen. Zum anderen sollte in diesem Zusammenhang die Kommunikationskompetenz durch Verwendung von fachbezogener Sprache mit Fachbegriffen, wie beispielsweise „die Spalte“, gefördert werden (vgl. PIKAS: Haus 4: Sprachbildung – Unterrichtsmaterial – Orientierung an der Hundertertafel).
Beide Teilziele sind in inklusiven Lerngruppen von besonderer Relevanz. Das erste Teilziel ist für leistungsschwächere genauso bedeutsam wie für leistungsstärkere Kinder, da das Wissen über die strukturellen Zusammenhänge das Rechnen erleichtern kann. Auch das zweite Teilziel spielte in dieser Lerngruppe eine besondere Rolle, da sie einen hohen Anteil von Kindern aufweist, die Deutsch als Zweitsprache erlernen. Zudem ist der Aufbau eines mathematischen Wortschatzes für alle Lernenden wichtig, da sie ihre Überlegungen nur durch die Nutzung korrekt gewählter Begriffe ausreichend illustrieren können.
Die folgenden Kinderdokumente entstammen der Untereinheit: „Wir erstellen ein eigenes Hundertertafel-Poster“. Diese beinhaltet eine aktiv-entdeckende Auseinandersetzung mit Hundertertafel-Ausschnitten. Die Schülerinnen und Schüler sollen die Positionierungen von Zahlen in Zusammenhang zu angrenzenden Zahlen untersuchen, um das Entdecken und Begründen der dekadischen Anordnung der Hundertertafel anzuregen.
 Abbildung 5
Abbildung 5
Aufgabe der Schülerinnen und Schüler war es, neben dem Finden der fehlenden Zahlen, einen Trick zu beschreiben, welcher das Finden von Zahlen in Zukunft vereinfachen sollte. Ausgehend vom Grundanforderungsblatt (Abb. 5, Mitte) wurden zwei analog aufgebaute Arbeitsblätter in einem niedrigeren Zahlenraum (Abb. 5, links) und in einem höheren Zahlenraum (Abb. 5, rechts) erstellt. Deutlich erkennbar sind der parallele Aufbau und die gemeinsame Aufgabe, welche allen Kindern aufträgt, eine Strategie zu finden, über die sich in der Reflexion trotz unterschiedlicher Arbeitsblätter ausgetauscht werden kann. Betrachtet man das „vereinfachte“ Arbeitsblatt, wird deutlich, dass nicht nur der Zahlenraum niedriger gehalten ist, sondern generell ein Unterschied im Schwierigkeitsgrad besteht. Die einzutragenden Zahlen sind hauptsächlich Zehnerzahlen und können bis auf eine Ausnahme additiv bestimmt werden (Abb. 6).
Das leistungsschwächere Kind konnte durch das Forschermittel „Pfeile“ (vgl. PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichts-Material – Forschermittelplakat, s. auch 'Forschermittel') die Struktur der Hundertertafel deutlich machen. Der Einerschritt in einer Zeile und der Zehnerschritt beim „Sprung“ in einer Spalte wurden erkannt und genutzt, um fehlende Zahlen zu finden. Die Pfeile dienten dem Kind somit nicht nur zum Verdeutlichen der Vorgehensweise, sondern waren zugleich Unterstützung, um die Struktur zu verinnerlichen.
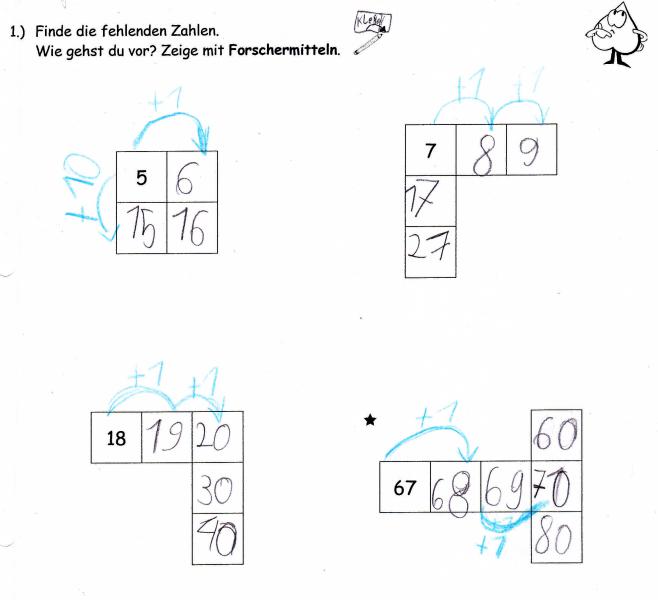 Abbildung 6
Abbildung 6
Auch das Kind mit erhöhtem Unterstützungsbedarf im Bereich Lernen (Abb. 7) konnte die leichteren Puzzleteile mit Unterstützung durch das Zwanzigerfeld (Wittmann & Müller, 1993; vgl. ‚Tipps und Herausforderungen‘) lösen.
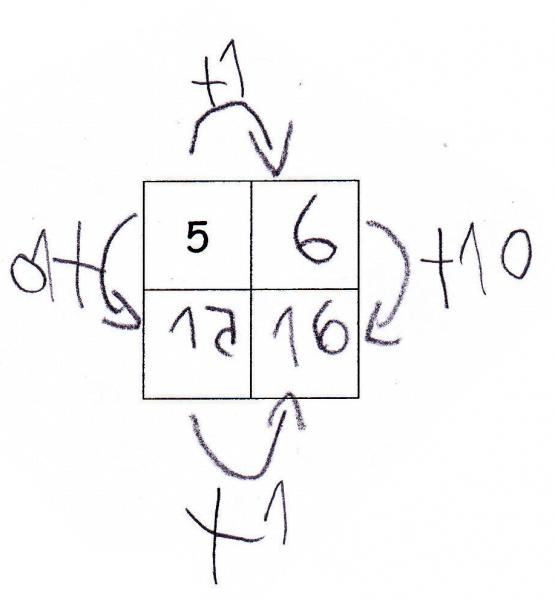 Abbildung 7
Abbildung 7
Leistungsschwächere Kinder, die versuchten ihre Vorgehensweise zu beschreiben, machten dies anhand von konkreten Zahlenbeispielen (Abb. 8). Der beschriebene Trick entspricht somit eher dem Zählen als einer verallgemeinerbaren ökonomischen Strategie.
 Abbildung 8
Abbildung 8
Entgegen der vorherigen Beschreibung (Abb. 8), bei der das Kind mit der linearen Zahlenfolge argumentiert, nutzt die Schülerin in Abbildung 9 schon die Lagebeziehungen der Zahlen auf der Hundertertafel („über“, „rechts von“). Es ist erkennbar, dass sie in der Hundertertafel bereits eine Orientierung hat, auch wenn sich diese zunächst auf einen kleinen Zahlenraum und die Zehnerzahlen beschränkt.
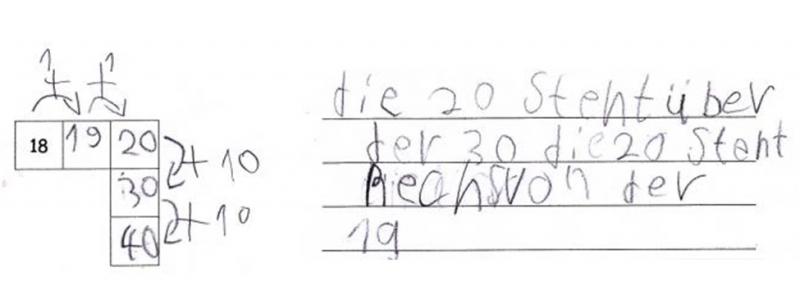 Abbildung 9
Abbildung 9
Auf dem Grundanforderungsarbeitsblatt sind ebenfalls vorwiegend Schritte „in positiver Richtung“ zu absolvieren. Eine beispielhafte Bearbeitung wird in den Abbildungen 10 und 11 verdeutlicht. Die Vorgehensweise des Schülers ist durch die Pfeilrichtungen und die Operationszeichen nachvollziehbar. Die Pfeile und Operationszeichen dienten dem Schüler zugleich auch als Orientierungshilfe.
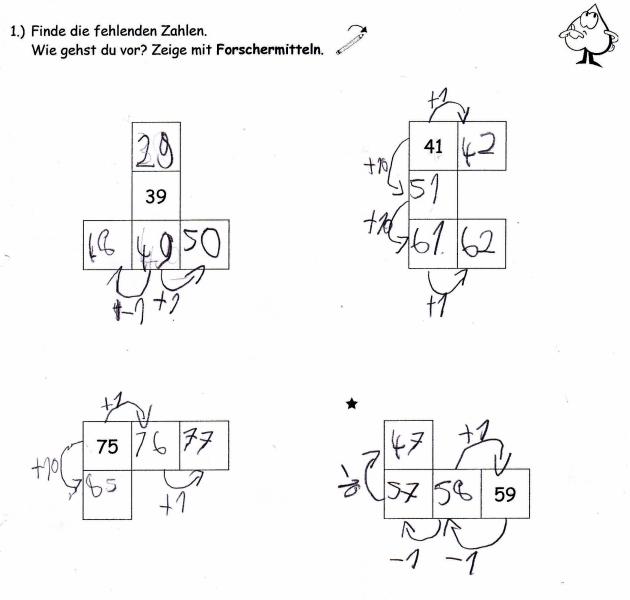 Abbildung 10
Abbildung 10
Die Beschreibung (Abb. 11) mit Zuhilfenahme von Fachwörtern („die Spalte“; „die Zeile“) ist allgemeiner („ima“) als bei den zuvor beschriebenen Dokumenten. Der Trick ist nicht an konkrete Zahlen gebunden, sondern auf alle Puzzleteile übertragbar.
 Abbildung 11
Abbildung 11
Auf dem Arbeitsblatt für leistungsstärkere Kinder finden sich vor allem Schritte „in negativer Richtung“ und keine Zehnerzahlen. Ein leistungsstarkes Kind (Abb. 12) verdeutlichte nicht jeden seiner bewältigten Rechenschritte, sondern nur solche, die zum Verstehen seiner Strategie ausreichten. Sein Vorgehen beinhaltete nicht nur Einer- und Zehnerschritte in den Zeilen und Spalten. Beim letzten Puzzleteil nutzte er Diagonalen und fand die fehlenden Zahlen durch Neuner- und Elfersprünge von der Startzahl aus.
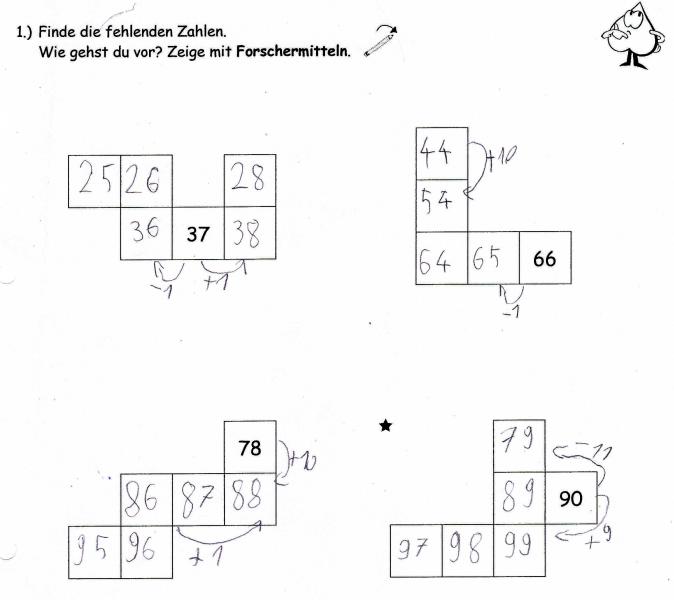 Abbildung 12
Abbildung 12
Das Vorgehen eines anderen Kindes (Abb. 13) zeigt, dass die fehlenden Zahlen auf unterschiedliche Weise gefunden werden können. Entgegen des vorherigen Dokuments geht dieser Schüler schrittweise von einer Zahl zur anderen vor.
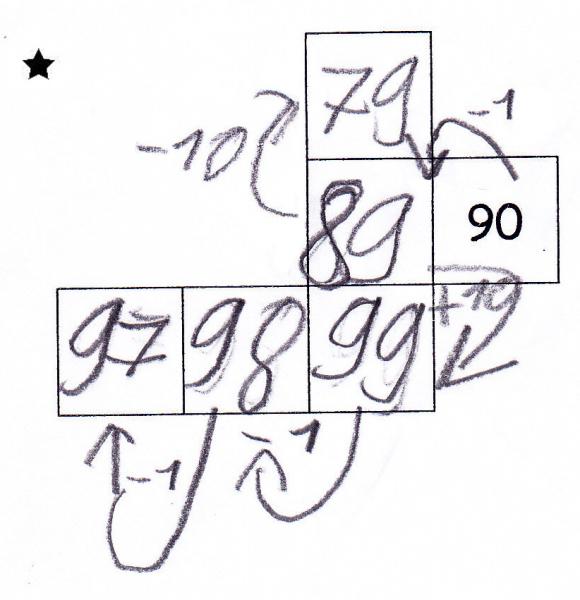 Abbildung 13
Abbildung 13
Die Beschreibung in Abbildung 14 der leistungsstarken Schülerin beinhaltet Fachwörter und kann als allgemeingültige Strategie („immer“) bezeichnet werden.
 Abbildung 14
Abbildung 14
Das Potenzial von verwandten Aufgabenstellungen wird meist erst in der Reflexionsphase bemerkbar, in welcher der kollektive Austausch aller gemachten Entdeckungen stattfindet. Um die Motivation der Schülerinnen und Schüler bis dahin konstant zu halten, ist die Arbeit an einem gemeinsamen Handlungsprodukt sinnvoll. Im Falle der dokumentierten Unterrichtsstunden durften die Kinder ihre gefundenen Zahlen in Kleingruppen auf großformatige Puzzleteile übertragen, welche im Anschluss daran mit den anderen Teilen zusammen ein Hundertertafel-Poster ergaben (Abb. 15).
Verwandte Aufgaben können demnach auch als Mittel dazu genutzt werden, ein übergeordnetes Handlungsprodukt zu erzeugen, zu dem jedes Kind etwas beitragen kann. Um das Hunderterfeld in Gänze zu erhalten, wurden alle Zahlen d.h. auch verschiedene Puzzleteile in unterschiedlichen Schwierigkeitsgraden benötigt, damit das Poster vervollständigt werden konnte (Abb. 16).
 Abbildung 15
Abbildung 15
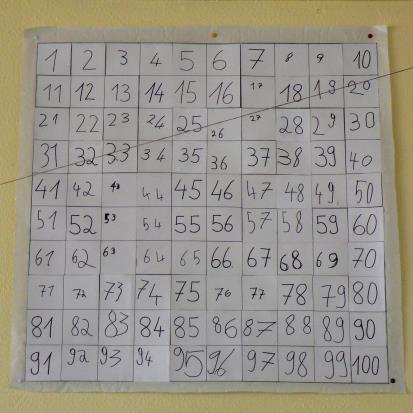 Abbildung 16
Abbildung 16
In der Reflexionsphase wurden exemplarisch einige Teile unterschiedlichen Schwierigkeitsgrades ausgewählt, welche gemeinsam an das Poster angebracht wurden. Schwerpunkt der Reflexion waren demnach die gefundenen Strategien und ihre Zweckmäßigkeit. Die Kinder erläuterten diese an ihren ausgefüllten Puzzleteilen, wodurch auch leistungsschwächere andere Strategien kennenlernten. Je nach verfügbarer Zeit, kann das Erstellen des Posters weggelassen werden. Die Kinder können ihre Entdeckungen dann an einem fertigen Poster erklären, auf dem sie ihre bearbeiteten Ausschnitte aber erst wiederfinden müssen.
Grundsätzlich lässt sich sagen, dass „verwandte Aufgabenstellungen“ oft Gemeinsamkeiten aufweisen. Sie sind leicht veränderbar und auf verschiedene Zahlenräume übertragbar, da der Fokus auf den prozessbezogenen Kompetenzen (vgl. KIRA: Problemlösen & Co – Kompetenzen im Mathematikunterricht) liegt. „Evident ist, dass dieses umso besser gelingt, je mehr sich auch im Mathematikunterricht eine Kultur des Erforschens, Entdeckens und Erklärens entwickeln [kann], je mehr das Beschreiben und Begründen zu einem natürlichen Bestandteil des Unterrichts geworden ist bzw. diese Grundhaltung der Kinder erhalten [wird]" (Selter, 2004, S. 34). Dies ist gerade dann der Fall, wenn das Kernanliegen der Unterrichtsstunde darin besteht, Strategien oder Rechenwege auszutauschen und das Vergleichen korrekter Ergebnisse einen geringeren Stellenwert einnimmt.
Weitere Anregungen
Ein weiteres Beispiel für ‚verwandte Aufgabenstellungen‘ entstammt einer Unterrichtsreihe zum Thema „Wir rechnen am Rechenstrich“ (vgl. ‚Offene Aufgaben einsetzen‘). In einer Unterrichtsstunde ging es darum, eine Subtraktionsaufgabe auf verschiedenen Wegen zu lösen (vgl. Arbeitsblatt „Rechenstrich ZR 100“). Auch hier sind die Rechenwege auf einen kleineren Zahlenraum (vgl. Arbeitsblatt „Rechenstrich ZR 20) übertragbar (vgl. Abb. 17).
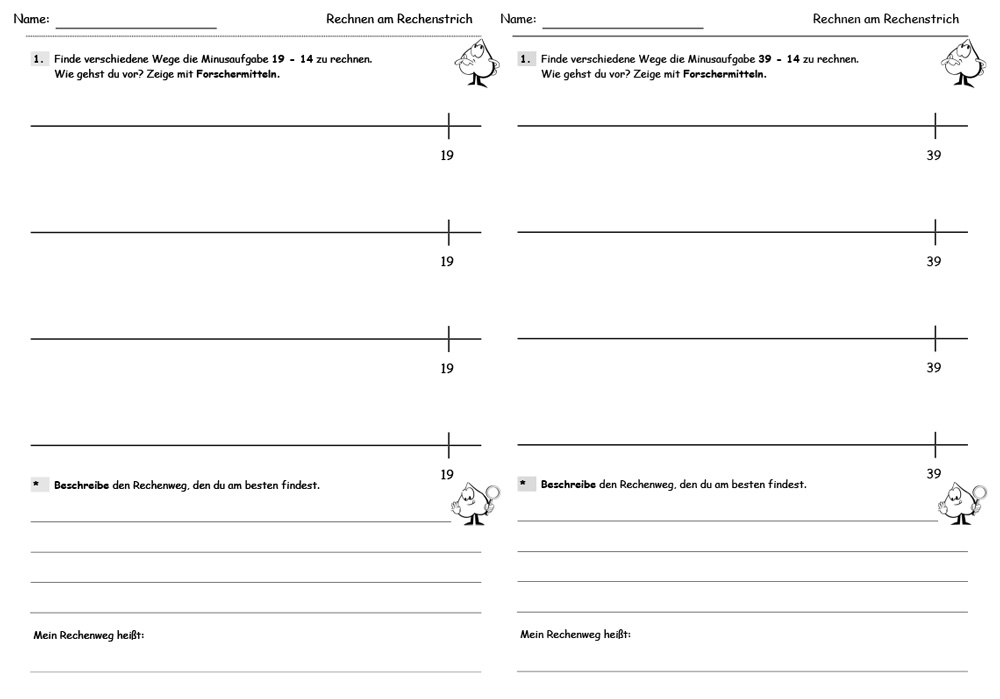 Abbildung 17
Abbildung 17
Kinder mit Unterstützungsbedarf können somit ihren Weg in die Reflexion mit einbringen. Ähnlich können auch analog aufgebaute Arbeitsblätter zu Additions- oder Multiplikationsaufgaben angefertigt werden.