Das Ziel, möglichst viele Freiräume zur individuellen Lernbegleitung zu schaffen, setzt einen hohen Anteil an Selbstständigkeit und Selbstorganisation der Lernenden voraus, die durch verschiedene Maßnahmen unterstützt werden können und müssen. Daher sollen im folgenden Bereich konkrete Ideen zur Unterstützung vorgestellt werden. Die im Folgenden konkretisierte Unterrichtsstunde dient beispielhaft der Anregung zur Gestaltung verschiedener Aspekte – wie der Stundentransparenz oder der Schaffung differenzierter Arbeitsplätze im Klassenzimmer – die in verschiedenen Formen umsetzbar sind. Die dargestellte Unterrichtsstunde ist eine Einheit aus einer Reihe zum mathematischen Inhalt des Halbierens, geeignet für den Einsatz in einer ersten Klasse. Dabei werden Kompetenzen thematisiert, die insbesondere in den Bereich „Zahlen und Operationen“ im Lehrplan (MSW 2008) für Nordrhein-Westfalen einzuordnen sind. Intention der gesamten Unterrichtsreihe ist der Kompetenzaufbau im Bereich des Verdoppelns und Halbierens von Zahlenmengen, um dies als eine mögliche Rechenstrategie zur Lösung von Additionsaufgaben kennen und anwenden zu lernen.
Die nachfolgende Gestaltung einer Einheit (siehe auch: Material) ist angelehnt an die im Bereich Hintergrund aufgeführte Idee des Lernens am gemeinsamen Gegenstand. Um die Möglichkeiten der Schaffung von Freiräumen für die Lehrkraft in alltäglichen Unterrichtsstunden darzustellen, werden diesbezüglich die einzelnen Phasen mit konkreten Ausgestaltungsmöglichkeiten und deren Unterstützungsmöglichkeiten vorgestellt.
Hinführung zur Aktivität - Strukturgebende Einstiegsphase

Abbildung: Möglichkeit zur Schaffung von Transparenz zum Unterrichtsverlauf
Die Einstiegsphase einer Unterrichtsstunde dient der inhaltlichen und organisatorischen Strukturierung der Unterrichtsstunde für die Lernenden. Ziel ist die inhaltliche Klärung und die Schaffung von Transparenz hinsichtlich des Stundenablaufes. Es kann hilfreich sein, den Ablauf in der gesamten Einheit zu visualisieren, sodass die Lernenden ihn nachhaltig in der gesamten Stunde nutzen können. Im Beispiel wird dies anhand von bildlichen Darstellungen, welche durch ausgeschriebene Wörter ergänzt werden können, umgesetzt. Organisatorische Fragen können dadurch nach der Fertigstellung eines Auftrages selbständig durch den Lerner erfasst und beantwortet werden. Der mathematischen Problementfaltung kommt in dieser Phase eine zentrale Bedeutung zu, die alle Lernenden ansprechen und aktivieren soll. Die Transparenz hinsichtlich des mathematischen Problems bietet die Visualisierung des Forscherauftrages, der während der gesamten Einheit nachgelesen werden kann. Einzuschieben ist an dieser Stelle, dass der Forscherauftrag bewusst vom Arbeitsauftrag zu differenzieren ist, sodass mit Hilfe der Bearbeitung des Arbeitsauftrags der Forscherauftrag (Nachdenkauftrag) thematisiert werden kann. Darüber stellt sich eine gemeinsame Probehandlung im Plenum als sinnvoll heraus. Zum vorliegenden Thema gilt es das Vorgehen zur Überprüfung einer Zahl in Bezug, ob diese ohne Rest halbiert werden kann – also gerade – ist zu thematisieren.
Der strukturgebenden Einstiegsphase kommt somit eine Schlüsselfunktion als Zugang und Vorbereitung der eigenständigen Aktivität zu, da die kindorientierte Klärung sowohl inhaltlicher als auch organisatorischer Aspekte den Grundstein eines selbstorganisierten Lernprozesses der Lernenden bildet.
Der anschließende Übergang in die Eigenaktivität der Lernenden ist flexibel zu gestalten. Lernende, die Klarheit bezüglich des Ablaufes der Einheit und Ideen zur Lösung des Arbeitsauftrages haben, bekommen die Möglichkeit am Arbeitsplatz außerhalb des Sitzkreises die Problemfrage selbstorganisiert zu bearbeiten. Für Lernende mit inhaltlichen Unklarheiten und Schwierigkeiten bei der eigenständigen Bearbeitung des Arbeitsauftrages „Halbiere selbstgewählte Zahlen! Warum ist das die Hälfte? Begründe!“, besteht die Möglichkeit, diese im Halbkreis zunächst zu thematisieren, ehe sie eigenständig die Aufgabenstellung bearbeiten. Hier kann gemeinsam ein möglicher Lösungsweg besprochen und erarbeitet werden. Dazu bietet es sich an das „gerechte Verteilen“ als Lösungsstrategie mit Hilfe des Zwanzigerfeldes und magnetischen Plättchen zu thematisieren. Die Offenheit hinsichtlich der Lösungsstrategien und des Zahlenraumes bietet die Möglichkeit, dass alle Lernenden diesen bearbeiten können (
siehe auch: PIKAS: Haus 8: Guter Unterricht – Fortbildungsmaterial). Ein solch flexibler Phasenübergang ermöglicht das Bearbeiten nach individuellem Tempo.
Hinsichtlich der Schaffung von unterrichtsintegrierten Diagnose- und Fördermomenten erlangt die Lehrkraft bereits an dieser Stelle durch die Aktivierung des Vorwissens, Aufstellens erster Vermutungen mit Begründungen und Überlegungen hinsichtlich des Probehandelns der Lernenden erste diagnostische Einblicke in die Lernvoraussetzungen und individuellen Zugänge der Schülerinnen und Schüler.
Selbstorganisierte Arbeitsphase
Die zweite Unterrichtsphase gliedert sich in drei Unterphasen. Sie ermöglicht die Nutzung einer Vielzahl von Möglichkeiten individueller Lernbegleitung, da alle Lernenden an dieser Stelle nach einer erfolgreichen Schaffung eines Zuganges zur Aktivität eigenständig an der Problemfrage arbeiten.
Die Situation zeichnet sich durch ihre Offenheit hinsichtlich der Aktivitätenorganisation aus. Das folgende Bild des Klassenzimmers verdeutlicht dies. Die selbstorganisierte Erarbeitungsphase ist dadurch gekennzeichnet, dass sich die Lernenden in unterschiedlichen Phasen der Erarbeitung befinden. Während einige nach einer längeren Einstiegsphase zunächst eigenständig an der Problemfrage arbeiten, tauschen sich andere Lernende bereits in der Austauschphase über gemachte Erkenntnisse aus. Welche organisatorischen Elemente förderlich zu Schaffung von Diagnose- und Fördermomenten sind, wird in den jeweiligen Phasen erläutert.

Abbildung: Individuelle Lernwege der Lernenden während der selbstorganisierten Arbeitsphase
Selbstorganisierte Arbeitsphase - Adaptive Arbeitsphase
In der adaptiven Arbeitsphase arbeiten die Kinder eigenständig in Arbeitstandems oder Einzelarbeit am Arbeitsauftrag der Unterrichtsstunde. Die Offenheit der Aufgabenstellung ermöglicht eine natürliche Differenzierung, sodass alle Schülerinnen und Schüler die Aufgabenstellung auf ihrem Kompetenzniveau bearbeiten können. Bei Problemen oder Unklarheiten sind die Schülerinnen und Schüler in der Phase dazu angehalten, sich zunächst selbständig bereitgestelltes Material, vor diesem fachlichen Hintergrund das Zwanzigerfeld und die Wendeplättchen zum Halbieren der Mengen, zu beschaffen.

Abbildung: Schaffung von Zugang zu unterstützenden Materialien mit Be-
schriftung
Dabei kann man die Lernenden unterstützen, indem im Klassenraum ein zugängliches und beschriftetes Matheregal zu finden ist, worin die Lernenden bekanntes didaktisches Material eigenständig finden können (Material, das sowohl der Diagnose, als auch der Förderung dienen kann). Weiterhin besteht die Möglichkeit Expertenkinder für verschiedene Fragestellungen zu bestimmen, die bei Fragen angesprochen werden können (siehe auch: PIKAS: Haus 8 - Informationsmaterial), wodurch es zu subsidiären Lernsituationen kommen kann, die zum mit- und voneinander Lernen beitragen (vgl. Wocken 1998). Die Lehrkraft ist somit nicht mehr die alleinige fachliche Anlaufstelle, sondern wird durch Helfersysteme und die Selbstständigkeit der Lernenden entlastet.
Das eigenständige Arbeiten aller Lernenden ermöglicht somit eine Vielzahl von Momenten, die zur individuellen Diagnose und Förderung genutzt werden können. Die folgenden Schülerdokumente zweier Lernender stellen dabei verschiedene Lösungswege dar, welche durch die Offenheit der Aufgabenstellung und Lösungsstrategien möglich sind, sodass alle Schülerinnen und Schüler die Erarbeitung nach individuellen Lernvoraussetzungen durchführen können.
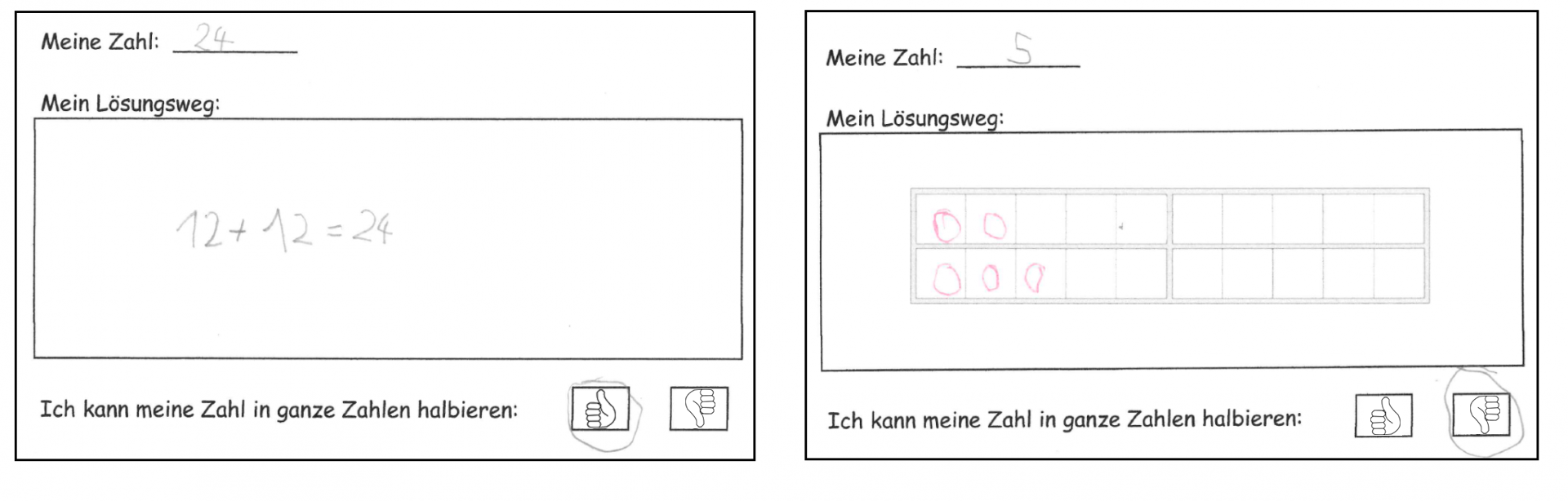
Abbildung: Lösungwege auf verschiedenen Darstellungsebenen (links: rein symbolische Darstellung; rechts: ikonische Darstellung am Zwanzigerfeld)
Selbstorganisierte Arbeitsphase - Strukturierte Austauschphase

Abbildung: Möglicher Leitfaden zum Ablauf des gemeinsamen Austausches
Die Bedeutung des Anregens von Austauschphasen und deren konkrete Umsetzung wird im Bereich gemeinsamen Austausch anregen ausführlich beschrieben, sodass an dieser Stelle lediglich ein kurzer Überblick gegeben wird.
Den Zeitpunkt, in die Austauschphase zu wechseln, bestimmen die Schülerinnen und Schüler individuell. Die visualisierte Stundentransparenz an der Tafel ermöglicht bei Unklarheiten einen Überblick hinsichtlich des nächsten Arbeitsschrittes. Die Mathekonferenz dient dem inhaltlichen Austausch von Entdeckungen und Ergebnissen und bildet mögliche Anlässe zum Argumentieren und Erklären des Forscherauftrages. Ein Leitfaden zur Struktur der genannten Mathekonferenzen bietet einen Überblick über den Ablauf des Gespräches und bildet damit eine weitere unterstützende Maßnahme hinsichtlich des selbstständigen Arbeitens. Zur Unterstützung der Verbalisierung der Erkenntnisse kann eine Visualisierung mit bedeutenden Begriffen und Sätzen im Klassenzimmer aufgehängt werden.
Für den Austausch in den Mathekonferenzen suchen sich die Lernenden im Klassenzimmer einen Platz, sodass Kinder, die sich in der adaptiven Erarbeitungsphase befinden, ungestört bleiben. Neben dem Austausch in Kleingruppen (Mathekonferenzen) sollte für die Lernenden die Möglichkeit bestehen sich auch nur mit einem Partner auszutauschen.
Dadurch wird auch denjenigen Lernenden ein Austausch ermöglicht, die den Herausforderungen des Austausches in einer Gruppe noch nicht bestehen können. Durch die Schaffung austauschanregender Situationen werden gezielt kooperative Lernsituationen angeregt (vgl. Wocken 1998).

Abbildung: Sammlung inhaltsbezogener wichtiger Wörter und Sätze
Das können zusammengeschobene Plätze im Sitzkreis sein, Plätze an der Fensterbank oder am separaten Arbeitstisch in der Multifunktionsecke oder auch einfach leerstehende Fensterbänke, auf dem Flur oder im Nebenraum, an denen die Lernenden sich ungestört austauschen können. Die Schaffung verschiedener Arbeitsplätze innerhalb eines Klassenzimmers bildet somit einen weiteren förderlichen Aspekt hinsichtlich der Gestaltung eines diagnose- und fördergünstigen Unterrichtes.
Selbstorganisierte Arbeitsphase - Individuell flexible Phase
Nach dem Austausch über Lernwege oder Ergebnisse in der Mathekonferenz besteht die Möglichkeit der individuellen Arbeit an einer vertiefenden Aufgabe hinsichtlich der Problemfrage, der Arbeit am Wochenplan oder den Erweiterungsaufgaben. Im Kontext dieser Einheit besteht die Möglichkeit für folgenden vertiefenden Arbeitsauftrag.

Abbildung: Möglicher Forscherauftrag als Erweiterungsaufgabe der individuell-flexiblen Phase
Der Einblick in die Intentionen und Inhalte der Erarbeitungsphase macht deutlich, dass die Lernenden auf individuellen Wegen am gemeinsamen Gegenstand vor dem Hintergrund individueller Lernvoraussetzungen arbeiten, währenddessen der Lehrperson Momente zur individuellen Lernbegleitung geschaffen werden. Deren konkrete Umsetzung wird im Bereich
Diagnose- und Fördermomente ausführlich beschrieben.
Reflexion der Aktivität - Auswertungsphase
Die abschließende Phase der Unterrichtsstunde bildet die Reflexions- bzw. Auswertungsphase, in der sich die Lerngruppe gemeinsam vor der Tafel treffen kann oder eine Teilgruppen-Reflexion in einer Kleingruppe stattfindet. Leitende Fragestellung der Phase bildet der zu Beginn transparent gemachte Forscherauftrag. Jetzt beschreiben die Schülerinnen und Schüler ihre Entdeckungen und verdeutlichen diese anhand von Beispielen. Zusammenhänge werden erschlossen und Erkenntnisse geordnet. Die Phase der Auswertung bietet der Lehrkraft die Möglichkeit der Diagnose hinsichtlich der gemachten Lernerfolge der Stunde. Besonders die Teilgruppenreflexion ermöglicht einen gezielten Einblick in die Vorgehensweisen einzelner Lerner.
Die konkreten Anregungen zu unterstützenden Maßnahmen in den verschiedenen Phasen einer Unterrichtsstunde verdeutlichen einmal mehr die Bedeutung strukturgebender Hilfsmittel für einen gelungenen Ablauf selbstorganisierten Lernens. Unterrichtsstunden mit einem hohen Anteil eigenständig organisierter Phasen der Lernenden bieten eine Vielzahl an Freiräumen für die Lehrkraft. Diese bildet damit nicht mehr das Zentrum des Lernens der Schülerinnen und Schüler, die nun eigenverantwortlich handeln. Diese Momente der Freiräume ermöglichen der Lehrkraft eine unterrichtsintegrierte individuelle Diagnose und Förderung einzelner Lernender, sodass sie aufgrund organisatorischer Überlegungen alltäglicher Bestandteil des Unterrichtes sind. Die individuelle Lernbegleitung einzelner Lernenden kann sich dabei sowohl auf den gemeinsamen Lerngegenstand beziehen aber auch inhaltsdifferente Kompetenzen thematisieren, sodass koexistente Lernsituationen je nach Bedarf geschaffen werden können (vgl. Wocken 1998). Demnach besteht die Möglichkeit, dass während sich andere Kinder in kooperativen Situationen über die mathematischen Inhalte austauschen, die Lehrperson einzelne Lernende in einer anderen Lernsituation individuell begleiten kann.
Dennoch ist es unumstritten, dass die Lernenden an das offene Arbeiten mit einer Vielzahl an selbstständigen Aktivitäten langsam herangeführt werden müssen. Erst ein ritualisiertes Ablaufen einer solchen Stunde eröffnet das gesamte Potential dieser Organisation, sodass die Lehrperson die Möglichkeit erfährt individuell begleiten zu können.