Beim entdeckenden Üben kann eine Vielzahl unterschiedlicher Aufgaben verwendet werden. Grundlage für diese Aufgaben zum Entdecken von Eigenschaften und Beziehungen können beispielsweise sein (in Anlehnung an Verboom, 2004, 8):
Zahlenmengen
-
1/3/5/7/9/11 (ungerade Zahlen)
-
4/9/16/25/36 (Quadratzahlen)
Zahlenpaare
-
3/6; 5/10; 7/14 (Verdopplungszahlen)
-
1/7; 2/6; 3/5; 4/4 (Zahlzerlegungen)
Zahlenfolgen
-
25/27/32/34/39/41… (Zahlenfolgen mit konstanten Veränderungen)
-
1/3/6/10/15… (geometrische Zahlenfolgen/ figurierte Zahlen (Folgezahlen können jeweils durch dieselbe Regel aus der vorangegangenen Zahl gebildet werden,): z.B. „Dreieckszahlen“)
Zahlentafeln
-
20er-Feld (Zahlbeziehungen im 20er-Raum)
-
100er-Feld (Zahlbeziehungen im 100er-Raum und Stellenwertsystem)
Operative Aufgabenserien
-
z.B. „Entdeckerpäckchen“, „Schöne Päckchen“; https://pikas.dzlm.de/node/554: Gleichmäßige Veränderungen einer oder mehrerer Zahlen im Term bewirken gleichmäßige Veränderungen oder Konstanz der Ergebnisse, Zahlenfolgen müssen erkannt werden. Eine Möglichkeit, solche regelmäßigen Aufgabenserien zu erzeugen, ist die gleichmäßigen Verschiebung von Fenster-Schablonen an den Zahlen- und Rechentafeln.
Aufgaben mit bestimmten Zahlenmustern
Substanziellen Übungsformate
-
Aufgabenformate mit der Struktur „Finde alle Zahlen / Aufgaben / Kombinationsmöglichkeiten…“
-
„Finde alle Zahlenpaare mit der Summe 1000, wenn in den Summanden jede Ziffer nur einmal vorkommen darf!“
-
„Finde alle Malaufgaben mit dem Ergebnis 20!“
-
„Finde alle Möglichkeiten, 5€ mit Münzen zu legen!“
In diesem Modul werden exemplarisch Übungsaufgaben des Typs „Operative Aufgabenserien“ und „Substanzielle Übungsformate“ dargestellt. Dies geschieht auch deshalb, weil z.B. Zahl- und Aufgabenbeziehungen (und damit z.B. Zahlenpaare oder Aufgabenpaare) unter einem anderen Schwerpunkt im Teilmodul „Vernetzendes Üben“ behandelt werden. Um außerdem zu zeigen, dass die Entwicklung prozessbezogener Kompetenzen kontinuierlich und über Jahrgangsstufen und mathematische Inhaltsbereiche hinweg erarbeitet werden sollte, werden in den dargestellten Übungstypen jeweils Aufgaben aus dem kleinen Einspluseins und dem kleinen Einmaleins behandelt. Anhand dieser vorgestellten Aufgaben werden exemplarisch einige Aspekte bei der Entwicklung prozessbezogener Kompetenzen näher erläutert.
Es gibt zahlreiche Möglichkeiten, die Lernenden bei der Entwicklung prozessbezogener Kompetenzen zu unterstützen (hierzu: PIKAS (pikas.dzlm.de/161) und PIKAS – kompakt (pikas-kompakt.dzlm.de/node/31)).
Zur Bereitstellung von Unterstützungsmaßnahmen bezogen auf bestimmte Schwierigkeiten beim entdeckenden Lernen sowie zur Differenzierung von Aufgaben siehe außerdem den Punkt „Unterstützungsmaßnahmen“ im Teilmodul „Sich verständlich machen“ (https://pikas-mi.dzlm.de/node/576).
Operative Aufgabenserien
Bei operativen Aufgabenserien werden eine oder mehrere Zahlen im Term der Aufgabe regelhaft verändert. Dabei bieten sich zahlreiche Lernchancen. Die Lernenden können…
-
die Aufgabenserien fortsetzen,
-
die Regel zur Fortsetzung formulieren,
-
nach Regelmäßigkeiten (Mustern) in den Aufgabenergebnissen suchen,
-
die Muster beschreiben oder
-
das Vorkommen der Muster begründen.
Die folgenden Aufgabenserien können als „Forscheraufgaben“ an der Einspluseins-Tafel bzw. der Einmaleins-Tafel entstehen, sie können aber auch ebenso als „Entdeckerpäckchen“ unabhängig von den Tafeln dargeboten werden.
Forschen an der Einspluseins-Tafel - Wir untersuchen die Diagonalen!
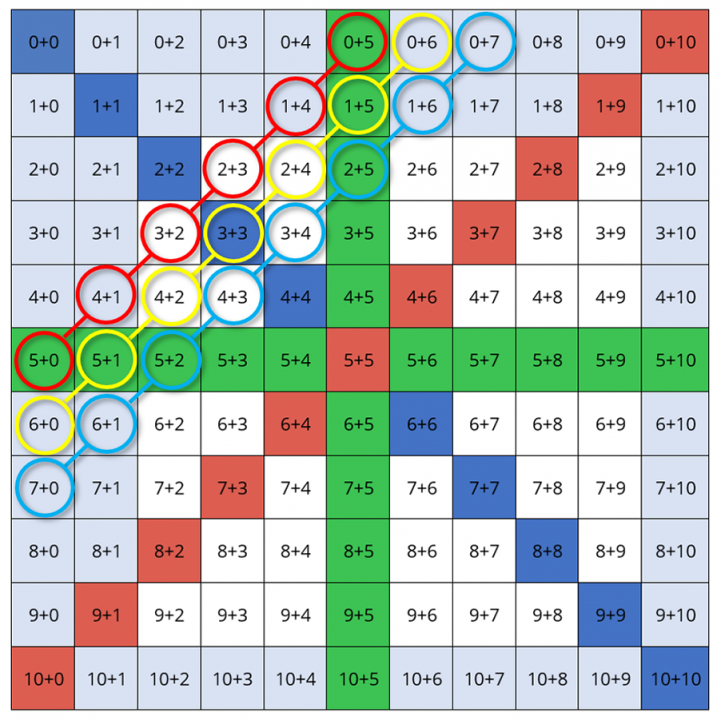
Forschen an der Einmaleins-Tafel - Wir untersuchen Partneraufgaben!
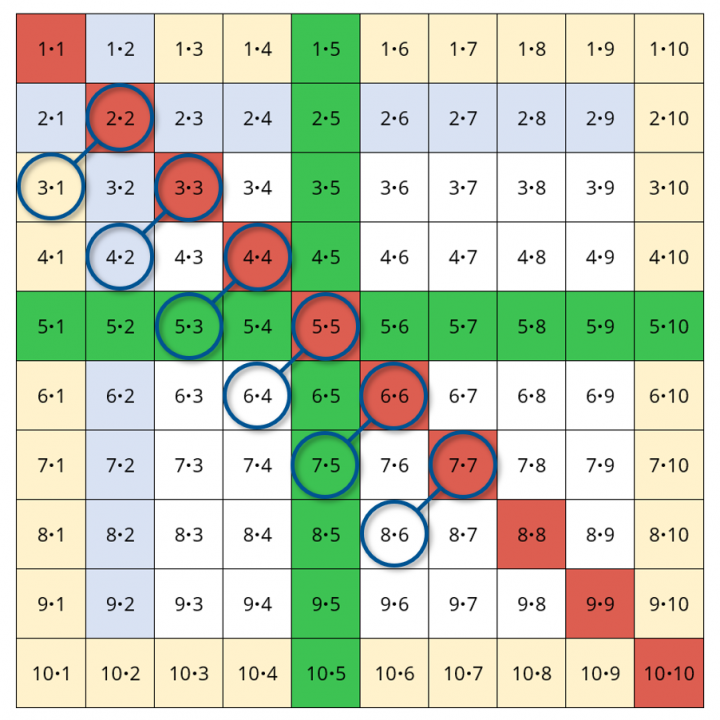
Arbeitsblätter und Einspluseins- bzw. Einmaleins-Tafeln lassen sich im Bereich "Material" herunterladen.
Mögliche Entdeckungen
1) Regel zur Fortsetzung:
-
Einspluseins: Der erste Summand wird immer um eins kleiner, der zweite Summand um eins größer (in der Aufgabenserie).
-
Einmaleins: Der erste Faktor wird um eins größer, der zweite um eins kleiner (Partneraufgabe). Beide Faktoren werden um eins größer (nach rechts).
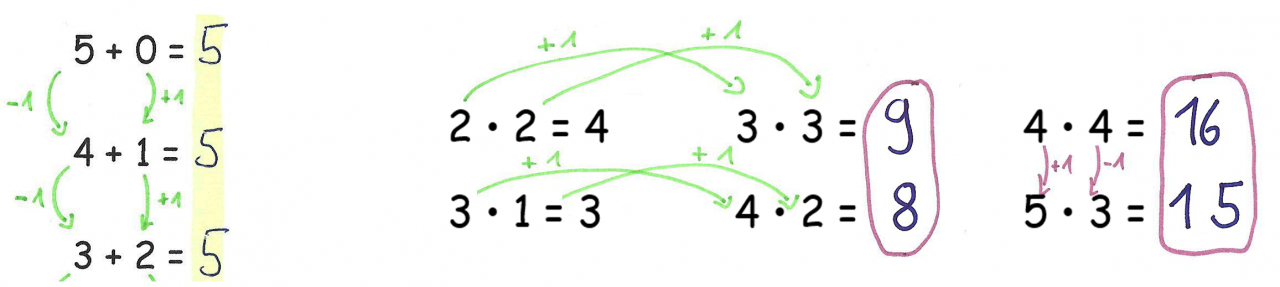
2) Tauschaufgaben (bei Einspluseins): Die obere Hälfte der Spalte sind Tauschaufgaben der unteren Hälfte. In der Mitte sind bei ungerader Aufgabenanzahl beide Summanden gleich.
Die Entdeckung ergibt sich aus der Regel, nach der die Aufgaben gebildet werden. Warum Tauschaufgaben der Addition dasselbe Ergebnis haben, lässt sich mit dem Teil-Ganzes-Konzept begründen. Dieser Zusammenhang wurde beim Vernetzenden Üben thematisiert (Kommutativgesetz) und ist anhand von Anschauungsmitteln begründet worden. Hier kann er nun wieder aufgegriffen werden.
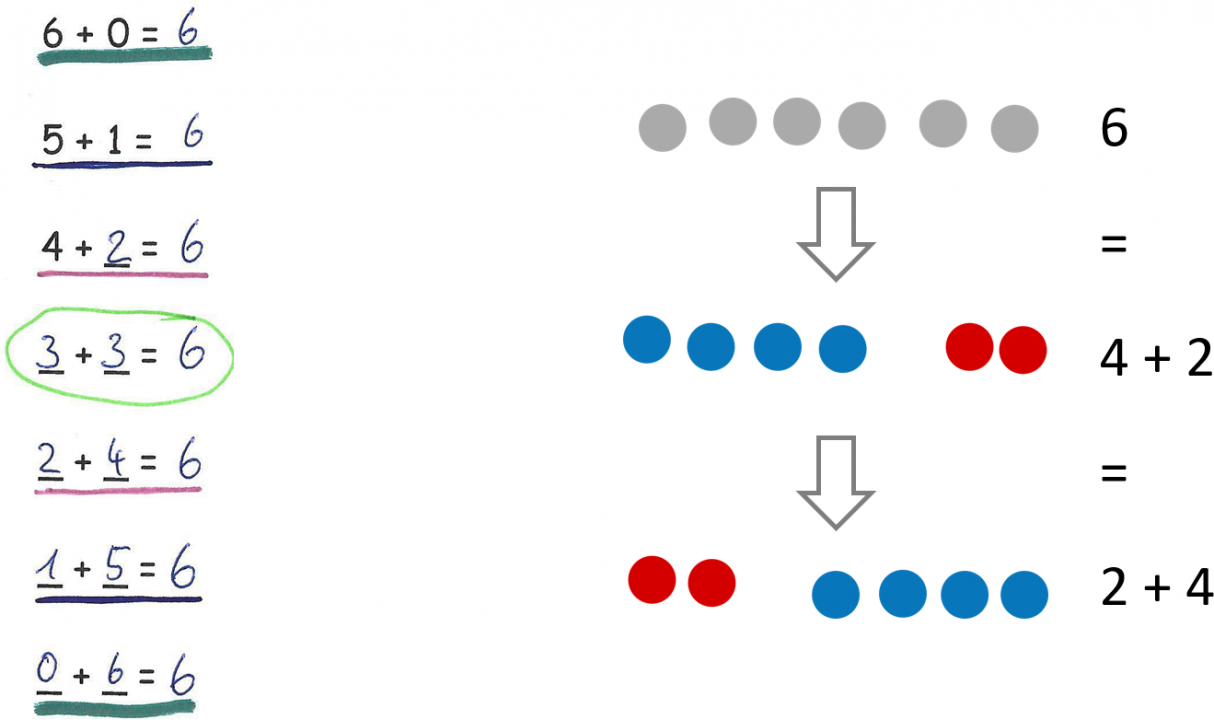
3) Konstanz der Summe (bei Einspluseins): Die Aufgaben einer Spalte haben dasselbe Ergebnis.
Die zugrundeliegenden Gesetzmäßigkeit (Konstanzgesetz: Gegensinniges Verändern), wurde beim Vernetzenden Üben im besten Fall materialgestützt erarbeitet („Aus ‚9 + 5‘ kann ich ‚10 + 4‘ machen, indem ich nur ein Plättchen verschiebe, die Gesamtzahl der Plättchen bleibt dabei gleich.“). Sie wird hier wieder aufgegriffen und bildet die Grundlage dafür, die Entdeckung in diesem Kontext zu begründen.
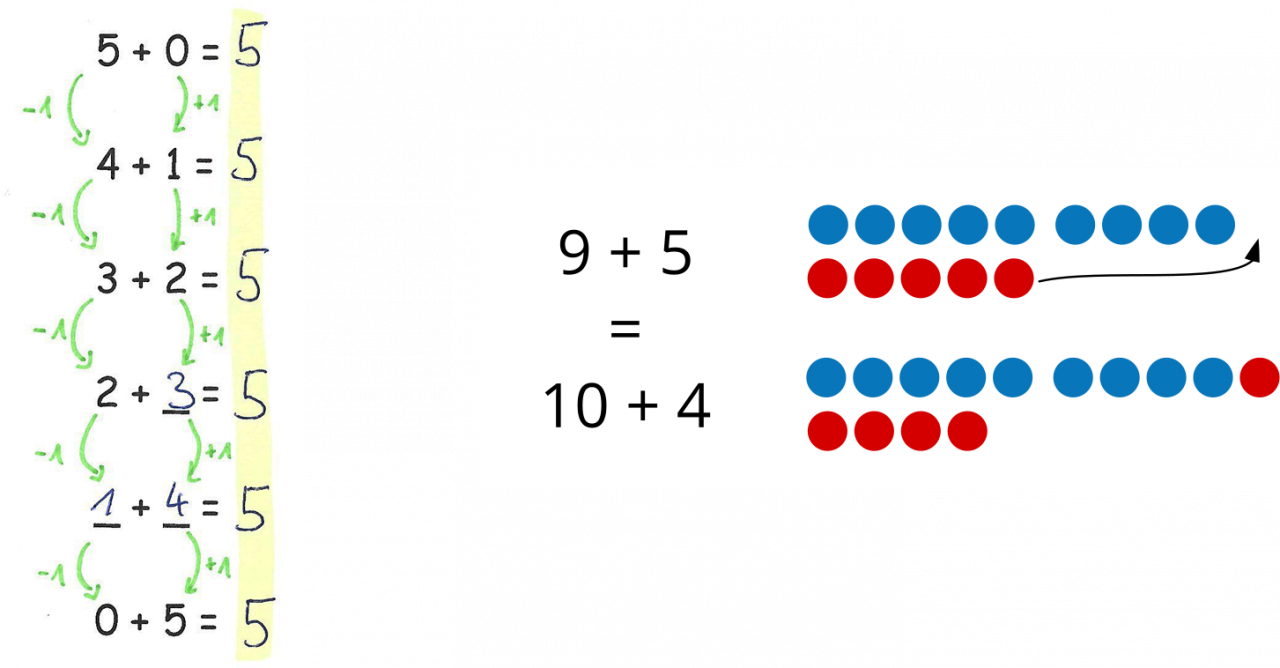
4) Konstante Differenzen der Produkte (bei Einmaleins): Die Differenz der Produkte zweier Partneraufgaben ist immer eins.
Eine mögliche Begründung kann gefunden werden, wenn an die Erkenntnisse angeknüpft wird, die beim vernetzenden Üben zu Aufgabenbeziehungen gemacht wurden. Der Fokus lag dort auf der Beziehung zwischen zwei Aufgaben, bei denen nur ein Faktor verändert wurde. Die Veränderungen zwischen diesen Aufgaben kann gut mit Plättchen oder Punktefeldern dargestellt werden. Auch hier lässt sich so begründen, warum das Ergebnis der Partneraufgabe jeweils um eins kleiner ist.
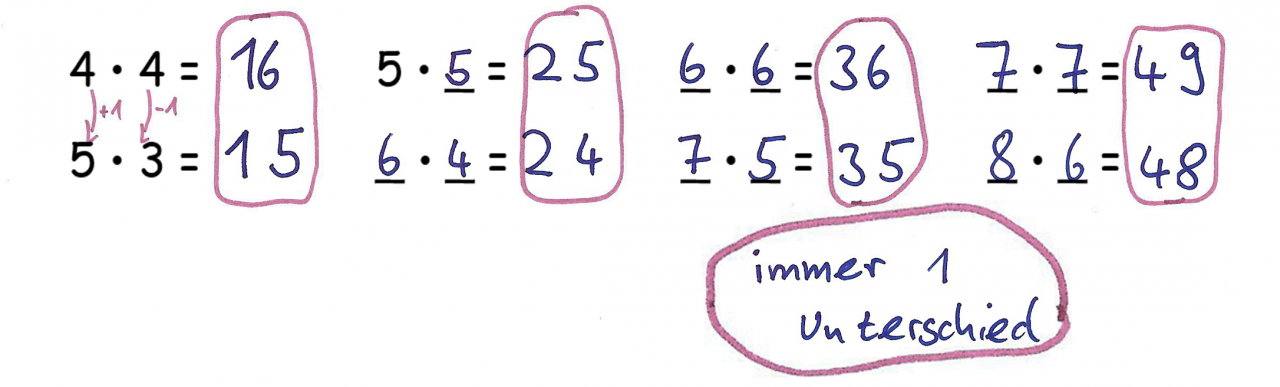
Forschermittel
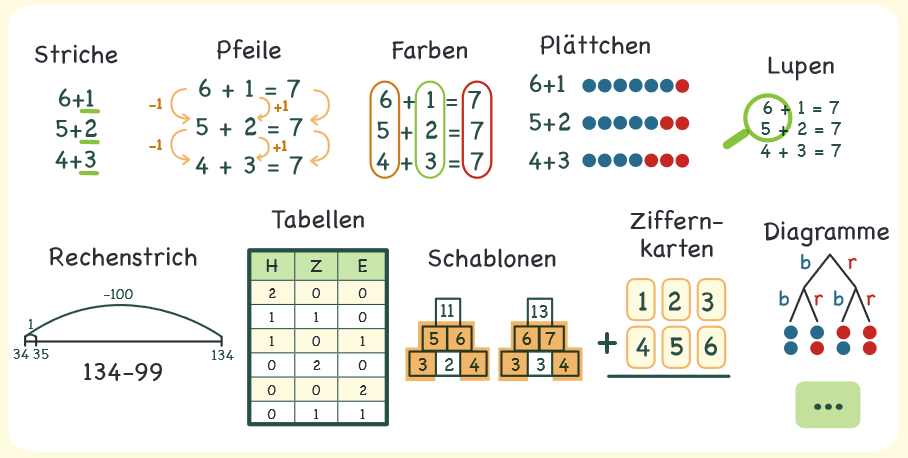
(Ausschnitt aus dem Plakat „Das nutzen Matheforscher“: PIKAS https://pikas.dzlm.de/node/561)
Forschermittel sind für die Lernenden – unabhängig von ihrer Klassenstufe, ihrem Leistungsniveau oder dem mathematischen Inhalt – für das Begreifen, Dokumentieren und Begründen von Entdeckungen und als Grundlage für den gemeinsamen Austausch darüber, ein bedeutendes Hilfsmittel (https://pikas.dzlm.de/node/556). Ihre Anwendung muss aber – wie jeder mathematische Inhalt auch – geübt werden.
Im dargestellten Beispiel sind alle gemachten Entdeckungen mit Forschermitteln markiert worden. Dabei können bestimmte Mittel besonders prägnant bestimmte Sachverhalte hervorheben, beispielsweise die Pfeile für regelhafte Veränderungen der Aufgaben wie in 1). Diese sind unabhängig vom mathematischen Inhalt oder der Klassenstufe sinnvoll, weswegen sie bereits in der ersten Klasse eingeführt werden und dann kontinuierlich weiter genutzt werden können.
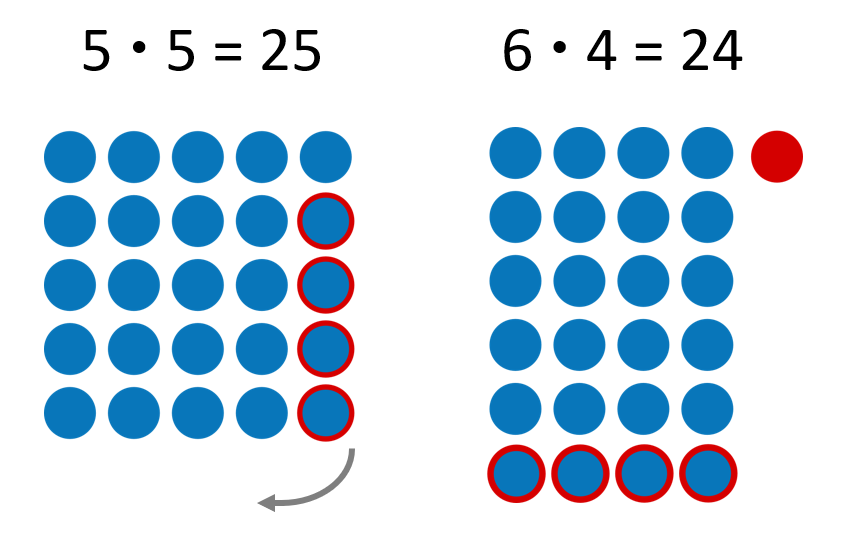
Für Begründungen und Beweise von Zusammenhängen oder, wie in diesem Fall, Rechengesetzen, eignen sich häufig Plättchen, wie in 2), 3) und 4). Zum Beispiel kann die Entdeckung bei 4), dass sich die Produkte der Partneraufgaben immer um eins unterscheiden, zwar direkt auf dem Arbeitsblatt gemacht und hervorgehoben werden. Warum das so ist, ist aber vor allem mit geeigneten Anschauungsmitteln möglich, in diesem Fall mit zwei „Plättchenrechtecken“, bei denen einzelne Plättchen verschoben werden, um die Partneraufgabe darzustellen.
Dabei sind die Erkenntnisse der früheren Übungsphasen des Grundlegenden und Vernetzenden Üben von Bedeutung, bei denen der Fokus auf der Verknüpfung von Grundvorstellungen, Zahl- und Aufgabenbeziehungen und geeigneten Anschauungsmitteln liegt. Diese werden hier wieder aufgegriffen und gefestigt, besonders, wenn ein gemeinsamer Austausch über die Begründungen zu den Entdeckungen stattfindet. Je mehr und je früher die Lernenden auf diese Weise Anschauungsmittel in ihre Begründungen mit einbeziehen, desto eher werden sie sie auch bei komplexeren Beweisen als Mittel nutzen können.
Substanzielle Übungsformate
Wie zu Anfang dieser Seite dargestellt, existieren zahlreiche substanzielle Übungsformate zu unterschiedlichen mathematischen Inhalten. Um zu zeigen, dass ähnliche Strategien über die Jahrgangsstufen und mathematischen Inhalte hinweg eingesetzt werden können, wird ein Übungsformat zu Zahlenmauern mit der Zielzahl 10 und eines zu Multiplikationsaufgaben mit dem Ergebnis 12 dargestellt.
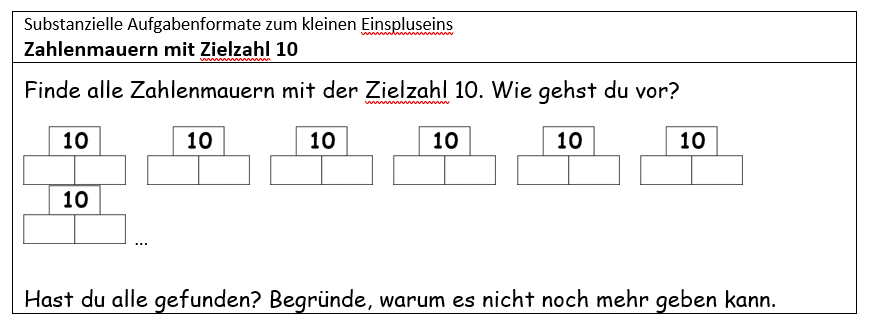

Problemorientierte substanzielle Übungsformate wie diese zeichnen sich unter anderem dadurch aus, dass sie unterschiedliche Vorgehensweisen ermöglichen. Die Lernenden können sowohl unsystematisch ausprobieren, um die Aufgabe zu lösen, sie können aber auch von Mal zu Mal geschickter und systematischer vorgehen. Entscheidend ist, dass sie genügend Raum und Anregungen bekommen, Erfahrungen zu dieser Art von Aufgabenstellung zu sammeln. Dies gelingt am besten, wenn die Lernenden ihre Vorgehensweisen reflektieren und darüber mit anderen in Austausch treten. Mögliche Vorgehensweisen, die ihnen diesen Übungsraum erlauben, werden im Folgenden erläutert:
Mögliche Vorgehensweisen und Forscherstrategien
Vorgehensweisen (exemplarisch)
1) Systematisch probieren: Einen Summanden/ Faktor systematisch verändern, den zweiten bestimmen.
Diese Strategie funktioniert für beide Aufgaben, mit dem Unterschied, dass bei der Addition alle Summanden bis 10 möglich sind, bei der Multiplikation aber nur bestimmte Faktoren in Frage kommen. Um alle Aufgaben zu finden und dies auch begründen zu können, sind der Anfang (der „erste“ Summand/ Faktor) und das Ende (der „letzte“ Summand/ Faktor) entscheidend.
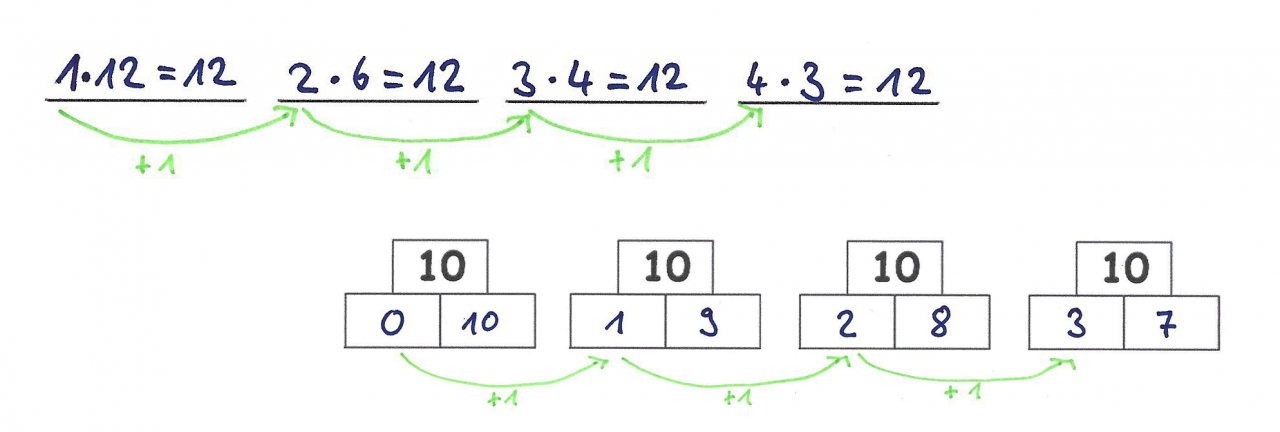
2) Sammeln und ordnen: Unsystematisch Aufgaben suchen, passende Aufgaben systematisch anordnen.
Auch diese Strategie kann für beide Aufgaben angewendet werden, ist aber zeitaufwändiger als 1). Ob alle Aufgaben gefunden sind, lässt sich nur über die Anordnung der gesammelten Aufgaben entscheiden, auch hier ist die Anfangs- und Endaufgabe entscheidend.
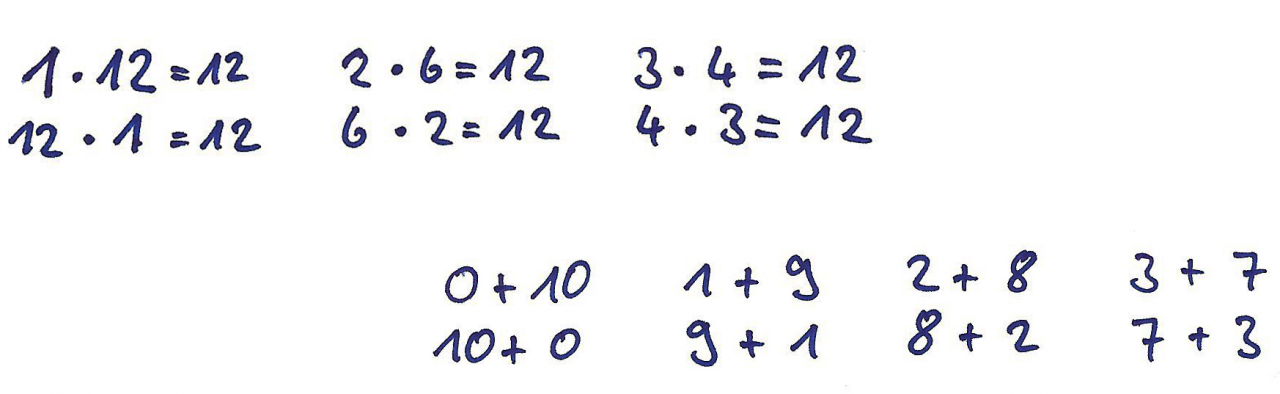
3) Tauschaufgaben nutzen: Zu einer passenden Aufgabe die Tauschaufgabe aufschreiben.
Um geschickt neue Aufgaben zu finden, kann jeweils die Tauschaufgabe genutzt werden. Mit dieser Strategie, können nicht alle Aufgaben gefunden werden, aber geschickt neue Aufgaben mit gleichem Ergebnis generiert werden. Dass Tauschaufgaben dasselbe Ergebnis haben, ist eine Erkenntnis aus dem Vernetzenden Üben, die hier genutzt und damit vertieft werden kann.
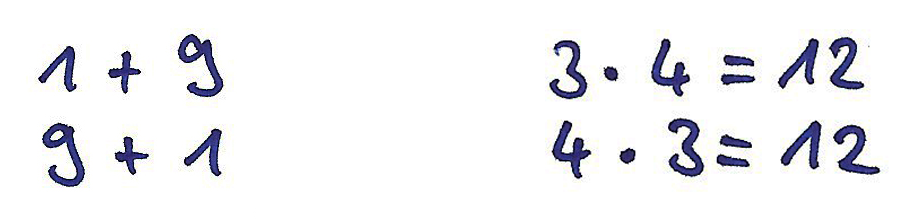
4) Vom Ergebnis ausgehen: Die Summe systematisch zerlegen/ das Produkt systematisch teilen.
Diese Strategie ist eng mit der ersten verwandt, der Vorteil wird aber deutlich, wenn das Zerlegen/ Teilen mit Anschauungsmitteln, wie Plättchen o.ä. umgesetzt wird. Auch die Begründung kann damit relativ leicht hergestellt werden.
 links: Zerlegen von 10 Plättchen, rechts: Teilen von 12 Plättchen
links: Zerlegen von 10 Plättchen, rechts: Teilen von 12 Plättchen
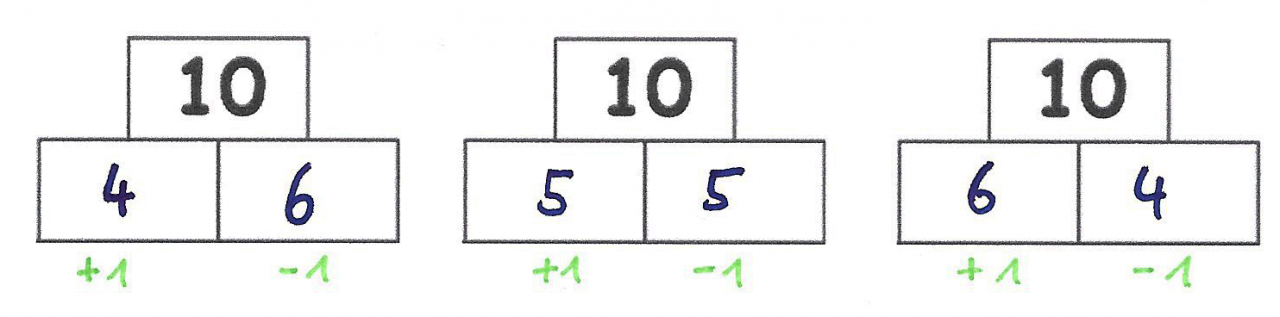
5) Gegensinniges Verändern (nur Einspluseins): Einen Summanden um eins vergrößern, während der andere Summand um eins verringert wird.
Diese Strategie beruht auf dem Konstanzgesetz und kann leichter von den Lernenden entdeckt werden, wenn sie schon ein paar Aufgaben wie in 1) systematisch probiert, oder wie in 4) die Summe systematisch zerlegt haben.
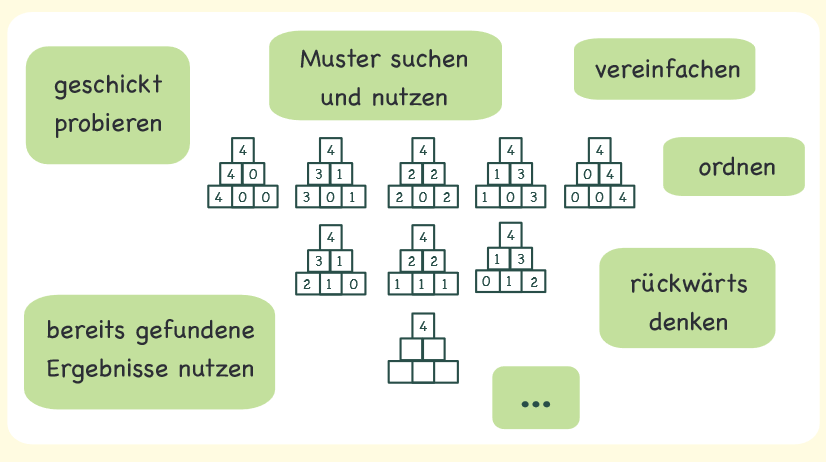
Forscherstrategien
 Ausschnitt aus dem Plakat „Das nutzen Matheforscher“: PIKAS https://pikas.dzlm.de/node/561
Ausschnitt aus dem Plakat „Das nutzen Matheforscher“: PIKAS https://pikas.dzlm.de/node/561
Forscherstrategien können, genau wie Forschermittel auch, von allen Lernenden unabhängig von ihrer Klassenstufe, ihrem Leistungsniveau oder dem mathematischen Inhalt genutzt werden. Die Vorgehensweisen und Strategien der Lernenden sollten bewusst zum Lerninhalt gemacht werden: Die Frage „Wie bist du vorgegangen?“ ist für die Entwicklung prozessbezogener Kompetenzen die entscheidende Frage, die für die Lernenden sowohl im Klassenverband als auch untereinander immer wieder Thema sein sollte. Eine Sammlung, ähnlich wie auf dem Ausschnitt oben, sollte also möglichst gemeinsam erstellt und weiterentwickelt werden.
In diesem Beispiel kommen z.B. diese Strategien vor:
-
„geschickt probieren“, wenn ein Summand/ Faktor systematisch verändert wird (wie in 1)),
-
„ordnen“, wenn passende Aufgaben systematisch angeordnet werden (wie in 2)),
-
„bereits gefundene Ergebnisse nutzen“, wenn Tauschaufgaben genutzt werden (wie in 3)) oder
-
„rückwärts denken“, vor, wenn das Ergebnis der Aufgabe zerlegt, bzw. geteilt wird (wie in 4)).
Für den Unterricht wesentlich bleibt dabei, dass den Lernenden während der Bearbeitung der Aufgabe die Möglichkeit gegeben wird, die Entwicklung von „geschicktem“ Vorgehen tatsächlich zu üben. Das bedeutet nicht nur, die Lernenden zum Reflektieren und Austauschen anzuregen, sondern auch ihnen genügend Raum und Anregungen zu geben, eigene Ideen (weiter-) zu entwickeln.
Bezogen auf das hier dargestellte Beispiel bedeutet dies, dass die Lernenden höchstwahrscheinlich bei der Bearbeitung der Aufgabe zwischen den Strategien wechseln werden, was wünschenswert ist: Eine Strategie kann zur nächsten führen, wie etwa beim gegensinnigen Verändern bei 5) dargestellt. Es ist auch denkbar, dass ein Schüler zunächst unsystematisch einige Aufgaben löst, sie ordnet (2), ihm dabei ein Muster auffällt, das er dann systematisch nutzen kann (1) und ihm bei der Arbeit an der Frage „Hast du alle gefunden? Warum kann es nicht noch mehr geben?“ klar wird, dass er auch vom Ergebnis hätte ausgehen können (4).