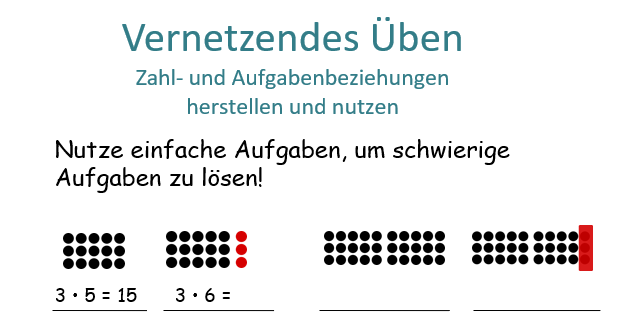
Beim vernetzenden Üben werden Zahl- und Aufgabenbeziehungen hergestellt, indem am Material gestützte Grundvorstellungen systematisch erweitert werden. Dabei geht es darum, Zusammenhänge für das Lösen von Aufgaben nutzen zu können.
Zahl- und Aufgabenbeziehungen
Zahlen und Operationen sind eingebunden in ein vielschichtiges Beziehungsgeflecht, das es zu erkunden gilt (Schulz & Schülke, 2017). Der Mathematikunterricht muss deshalb von Beginn an und mit allen Kindern „das ‚Denken in Beziehungen‘ in den Mittelpunkt“ (ebd., 140) stellen, um tragfähige Grundvorstellungen aufzubauen, die wiederum die Basis für die Entwicklung flexibler Rechenstrategien bilden.
Hierbei lassen sich grundsätzlich drei Arten von Beziehungen unterscheiden:
1. Zahlbeziehungen
Darunter wird die „Fähigkeit, eine Zahl in ihrer Beziehung zu anderen Zahlen ‚sehen‘ und verstehen zu können“ (ebd.) verstanden, sowohl auf ihre kardinalen Aspekte (z.B. Teil-Ganzes-Konzept) als auch ordinalen Aspekte (z.B. Nachbarzahlen) bezogen.
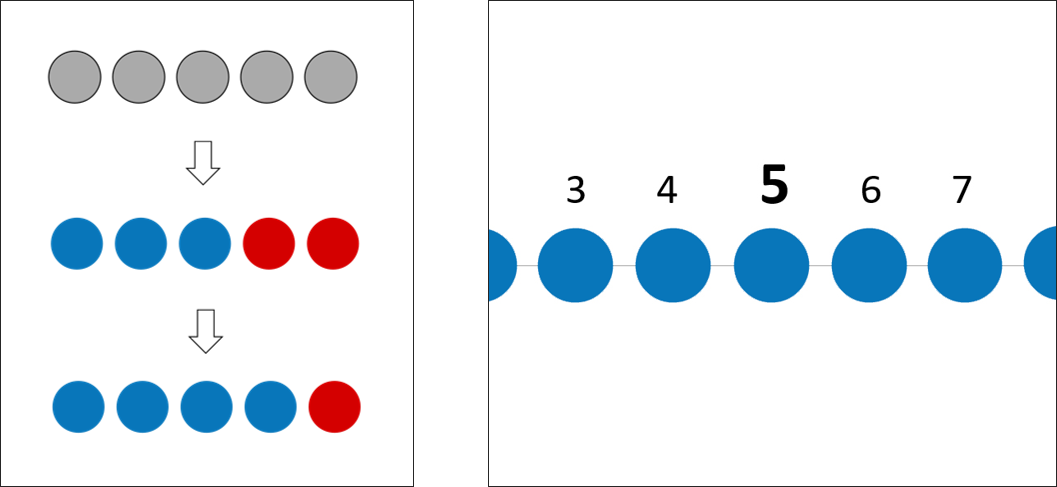 Teil-Ganzes-Konzept (links): die "5" als "2 und 3" oder "1 und 4"
Teil-Ganzes-Konzept (links): die "5" als "2 und 3" oder "1 und 4"
und Ordinalzahlaspekt (rechts): die "5" zwischen ihren Nachbarzahlen
2. Beziehungen zwischen Aufgaben
Hiermit sind vor allem Ableitungen von verwandten Aufgaben gemeint, also das Nutzen von einfacheren Hilfsaufgaben, um schwerere Aufgaben zu lösen. Grundlage bilden die Rechengesetze der elementaren Arithmetik (Selter & Zannetin, 2019, beispielhaft konkretisiert):
-
Kommutativgesetz: 2 + 6 = 6 + 2
-
Assoziativgesetz: (6 + 8) + 2 = 6 + (8 + 2)
-
Distributivgesetz: 8 • 7 = 5 • 7 + 3 • 7
-
Konstanzgesetz: 9 + 5 = 10 + 4
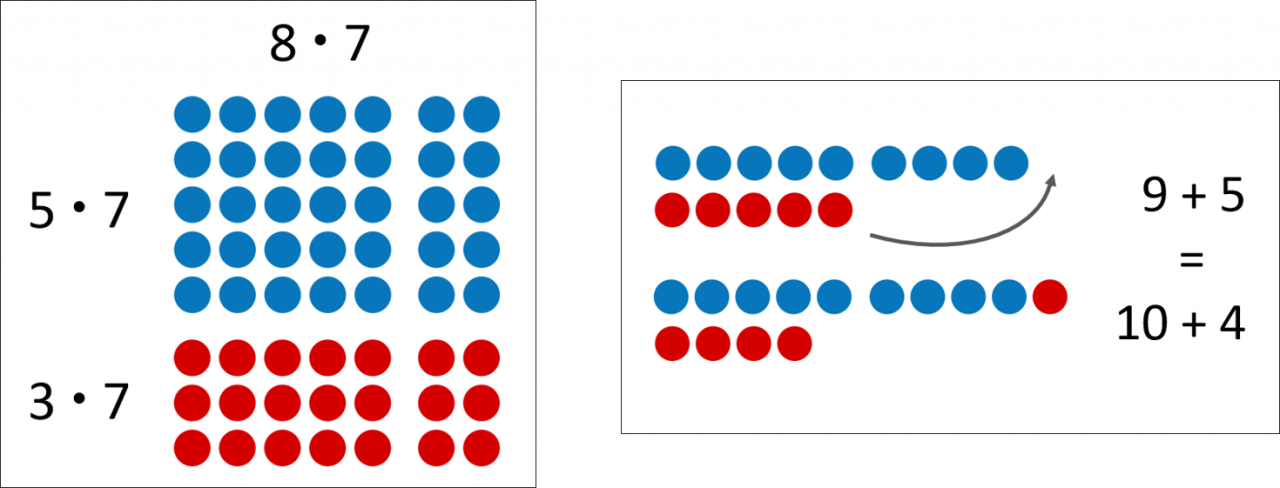 Distributivgesetz (links) und Konstanzgesetz (rechts)
Distributivgesetz (links) und Konstanzgesetz (rechts)
3. Beziehungen zwischen Rechenoperationen
Hiermit ist die Vernetzung der vier Grundrechenarten untereinander gemeint (Götze, Selter, Zannetin, 2019), also z.B.:
-
die Subtraktion als Umkehroperation der Addition (21 – 19 = 2 und 19 + 2 = 21) oder
-
die Division als Umkehroperation der Multiplikation (24 : 6 = 4 und 6 • 4 = 24)
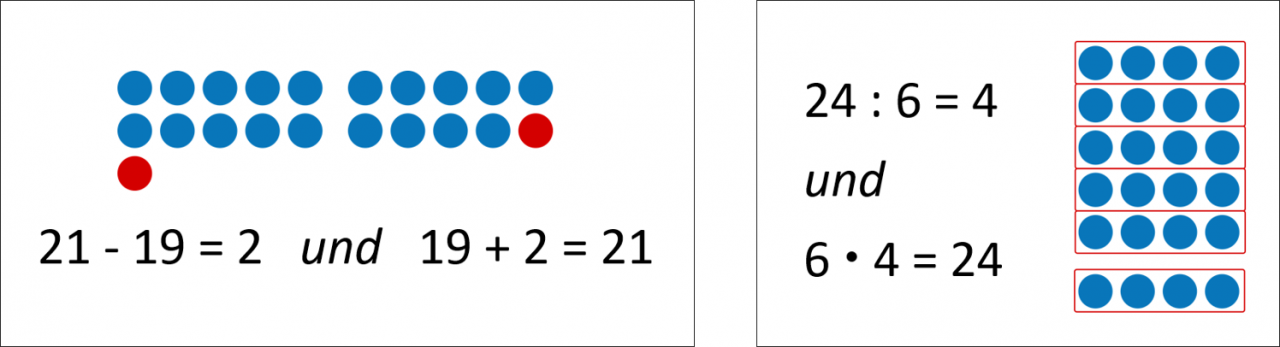 Subtraktion als Umkehroperation der Addition (links) und Division als Umkehroperation der Multiplikation (rechts)
Subtraktion als Umkehroperation der Addition (links) und Division als Umkehroperation der Multiplikation (rechts)
Rechenschwierigkeiten
Kindern mit Schwierigkeiten im Mathematiklernen fällt es oft schwerer als anderen, Beziehungen und Strukturen zu erkennen, selbst wenn diese im Unterricht explizit herausgearbeitet werden (Gaidoschik 2015). Mit Blick auf den umfangreichen Lehrplan könnte man sich die Frage stellen, ob es für Kinder mit Rechenschwierigkeiten nicht sinnvoller wäre, wenn sie vor allem wichtige Rechenaufgaben automatisieren und Rechenverfahren nachahmend anwenden können.
Ein solches Vorgehen widerspricht allerdings nicht nur der grundsätzlichen Auffassung des selbstständigen, aktiven Lernens, von der gerade auch Kinder mit besonderen Unterstützungsbedarfen profitieren (ebd.), es ist auch ineffektiv, da es Kinder zu unflexiblen Rechnern macht, die bei neuen Zahlenräumen oder Aufgabenstellungen nur unzureichende Lösungsstrategien zur Verfügung haben:
Es ist gerade für [Kinder mit Rechenschwierigkeiten] notwendig, Zusammenhänge zwischen Zahlen und Termen zu erfassen, um überhaupt nachhaltig mathematisch lernen zu können. Ziel der Förderung muss daher stets der langfristige, verstehensorientierte Aufbau eines Wissens sein, das sich auf das Verständnis mathematischer Zusammenhänge stützt. […] Eine solche Stütze stellt sich ein über die Konzentration auf basale mathematische Inhalte, mathematische Zusammenhänge im Zuge produktiver Übungen und die Verwendung grundlegender Veranschaulichungen. (Häsel-Weide, Nührenbörger, Moser-Optiz & Wittich 2013, 32)
Trotzdem bleibt die Herausforderung bestehen, dass Kinder mit Rechenschwierigkeiten in der Regel mehr Zeit und gezieltere Anleitung benötigen, um Zahl- und Aufgabenbeziehungen herstellen und nutzen zu können (ebd.). Dabei sind folgende Prinzipien des vernetzenden Übens hilfreich:
Ganzheitliche Vorgehensweise
Hilfreiche Beziehungen zwischen Aufgaben können besser entdeckt werden, wenn die gleiche Entdeckung bei möglichst vielen Aufgaben gemacht werden kann (Gaidoschik 2015). Beispielsweise kann das Ergebnis der Aufgabe 9 • 4 von der Hilfsaufgabe 10 • 4 abgeleitet werden. Dass dies kein Sonderfall ist, sondern in allen Reihen funktioniert, können Kinder aber erst begreifen, wenn die Reihen nicht einzeln nacheinander eingeführt werden, sondern alle zur Bearbeitung zur Verfügung stehen (ebd.). „Wird ein Zusammenhang erarbeitet, dann jeweils sofort im ganzen Einmaleins, quer über alle Reihen hinweg“ (ebd., 17). Nur so können die Kinder herausarbeiten, wie genau dieser Zusammenhang überall funktioniert, also die Regelhaftigkeit entdecken. Insgesamt sichern und automatisieren sie also Strategien statt Ergebnisse.
Operative Aufgabenpaare und Aufgabenserien
Nachbaraufgaben, wie im Beispiel oben, spielen insgesamt eine wichtige Rolle, denn „in vielen Fällen [kann] durch das Nutzen von Nachbaraufgaben eine schwierige Aufgabe auf eine einfache zurückgeführt werden“ (Häsel-Weide, Nührenbörger, Moser Opitz & Wittich 2013, 140). Damit die Beziehungen zwischen Nachbaraufgaben verstanden und genutzt werden können, müssen sie zunächst explizit und in möglichst mehreren Darstellungsformen beschrieben werden. Dabei sollten Fragestellungen im Sinne des operativen Prinzips („Was geschieht, wenn…?“) im Vordergrund stehen, z.B.: „Was geschieht mit dem Ergebnis, wenn ich den ersten Summanden um 1 erhöhe?“ oder „Was geschieht mit dem Ergebnis, wenn ich den 1. Faktor um 1 vermindere?“
„Schöne Päckchen“ bzw. „Entdecker-Päckchen“ sind Beispiele für operative Aufgabenserien. Wenn schon hier der Fokus auf die Beziehungen zwischen den Aufgaben gelegt wird und nicht nur auf das Ergebnis, eröffnen sich den Schülerinnen und Schülern zahlreiche Lernchancen im Vernetzen von Aufgaben.
Kernaufgaben als Ausgangspunkt für Ableitungen
Kernaufgaben sind Aufgaben, die von den meisten Schülerinnen und Schülern leichter gelöst werden können und die deshalb als Ausgangspunkt für schwierigere Aufgaben genutzt werden können. Beim Einspluseins sind das z.B. Verdopplungs- und Halbierungsaufgaben oder Zerlegungen der „10“ (ebd.). Beim Einmaleins gehören die 1er-, 2er-, 10er- und 5er-Reihe zu den Kernaufgaben, die für Ableitungen genutzt werden (Gaidoschik 2015). Entscheidend ist, dass die Schülerinnen und Schülern lernen, Kernaufgaben als Ausgangspunkt für Ableitungen auch als solche zu erkennen.
Grundvorstellungen aktivieren und festigen
Vernetzendes Üben ist gerade auch für Kinder mit Lernschwierigkeiten effektiv, weil dabei Grundvorstellungen immer wieder aktiviert und damit abgesichert werden. „Ein Kind, das bei 9 • 4 an 10 • 4 denkt und sich 6 • 8 aus 5 • 8 erschließt, aktiviert Grundvorstellungen zum Multiplizieren. Es gibt den Aufgaben einen Sinn und nutzt diesen Sinn, um die Aufgaben auszurechnen“ (Gaidoschik 2015, 18, Hervorhebung i. O.). Der Gefahr, dass Kinder sich beim verfrühten „gedankenlosen“ Automatisieren Aufgaben und Ergebnisse nicht mehr vorstellen, sondern wie Vokabelpaare auswendig lernen, kann damit entgegengewirkt werden.